基于深度神经网络的多星测控调度方法

李长德，徐伟，徐梁，王燕

航天恒星科技有限公司，北京 100086

1 引言

随着各国对空间领域应用的重视，空间技术迅猛发展，在轨卫星的数量不断增加，对测控资源的需求越来越大[1]，多星测控资源调度成为卫星应用领域的重要挑战。多星测控调度(multi-satellite TT&C scheduling，MSTCS)问题是指在多星测控需求和测控资源一定的背景下，研究如何对众多卫星的各类测控需求进行管理和调度，通过合理地分配测控资源，更好地满足卫星的测控需求，使得卫星发挥最大的应用效能，并对航天顶层设计提供指导。MSTCS问题是一个高复杂、强冲突、多关联约束的NP问题。传统测控资源调度算法在针对大量不同种类卫星进行测控调度时面临运算时间较长、效率低下、复杂度高且适应性差等问题。

面对MSTCS问题的现状，国内外涌现出许多相关研究，如数学规划、CSP模型、禁忌搜索及人工智能等求解方法。其中，文献[2]提出CSP模型方法，文献[3-4]提出约束规划方法。这些方法可以精确的描述问题，但是考虑的约束过多且复杂，难以求解，文献[5-6]提出使用遗传算法，文献[7]提出蚁群算法解决测控调度问题，这些禁忌搜索方法设计灵活，求解效率较高，但是领域知识依赖性较强。文献[8-10]提出基于神经网络解决测控资源调度，由于网络结构较为简单，只有一层隐含层，结果精度较差。

为了解决以上问题，本文提出了基于深度神经网络(deep neural networks,DNN)的多星测控调度方法。深度神经网络层级较多，结构稳定，具有强大的计算能力，学习能力强且能学到深的特征。当前DNN算法已在推荐算法[11-12]、航天器容错控制[13]、空间目标识别[14]等方面解决了很多问题。该方法抽取调度过程中对调度结果有重要影响力的属性作为DNN的特征值构建DNN模型，并通过预处理将测控任务与测控资源间的全匹配缩减为有效匹配，降低DNN的特征维度及训练难度。最后根据真实的卫星和测站参数，使用STK模拟真实场景，验证了本文提出方法的有效性和高效性。

2 多星测控调度特性分析与建模

使用DNN算法解决MSTCS问题，首先需要确定DNN的输入，即特征值的选择与抽取。为选择出合适的属性作为DNN算法的特征值，对调度过程中涉及的实体进行建模，明确各个实体的属性；然后分析调度过程中的各种约束，进行目标约束建模。将实体模型与约束模型结合，选择对调度结果有影响的因子，数值离散处理后作为DNN算法的特征值。

2.1 实体模型

测控资源调度问题涉及的实体主要有卫星、测控设备、测控任务、用户偏好、可见时间弧段[15-16]。

(1)卫星

其属性定义为：Satellite={Satellite1,Satellite2,…,Satellitem},Satellitei∈Satellite，指的是第i个卫星，i=1,2,…,m。Satellitei={SIDi,SNamei,STatusi,STypei,SPi,SCati,SFi,SLifei,SDSi}，属性的含义分别为：SID为卫星标识符，SName为名称，STatus为状态，SType为卫星轨道类型，SP为卫星优先级，SCat为卫星属性(飞船、军用、民用等)，SF为测控频段，SLife为卫星运行阶段，SDS为设备偏好集合。

(2)测控设备

属性定义为：Equipment={Equipment1,Equipment2,…,Equipmentn}，Equipmenti∈Equipment,指的是第i个设备，i=1,2,3,…,n。Equipmenti={EqIDi,EqNamei,EqDFi,EqUri,EqStatusi,EqStarttimei,EqEndtimei,EqPri,EqSti,EqServcei}，属性的含义分别为：EqID为设备标识符，EqName为名称，EqDF为设备频段，EqUr为设备利用率，EqStatus为设备状态，EqStarttime为设备可用开始时间，EqEndtime为设备可用结束时间，EqPr为根据设备的运行参数以及历史故障率等得到的设备优先级，EqSt为设备切换时间、EqServce服务能力(遥测、遥控、测轨、全能型等)。

(3)测控任务

属性定义为：Task={Task1,Task2, …,Taskn}，Taski∈Task，指的是第i个测控任务，i=1,2,3,…,n。Taski={TaIDi,TaNamei,Tasi,Taei,TaSati,TaTyi,Tapli, TaProi,Tacyi,TaDi,TaPi,TaTwi,TaSpliti,TaMinci,TaMaxci,TaMindi,TaMaxdi,TaMinsi,TaMaxsi,UIDi,TaStatusi}。属性对应的含义分别为：TaID为任务ID，TaName为名称，Tas为开始时间，Tae为结束时间，TaSat为所属卫星，TaTy为任务类型(遥测、遥控、注入、测轨)，Tapl为任务性质(正常、应急)，TaPro为任务类别(实战、联调)，Tacy为周期性，TaD为任务时长，TaP为任务优先级，TaTw为任务执行阶段(长管、应急等)，TaSplit为是否可拆分，TaMinc为最小分解段数，TaMaxc为最大分解段数，TaMind为最小分解弧段时长，TaMaxd为最大分解弧段时长，TaMins为最小分段间隔，TaMaxs为最大分段间隔，UID为用户偏好ID，TaStatus为执行状态。

(4)用户偏好

属性定义为：UP={UP1,UP2,…,UPn}，UP为用户偏好集合，UPi∈UP，指的是第i个用户偏好，i=1,2,3,…,n。UPi={UIDi,Utpi,Ucti}。属性对应的含义分别为：UID为用户偏好标识符，Utp为用户偏好类型(时间偏好、设备偏好等)，Uct为偏好内容。

(5)测站对卫星的可见时间窗口

属性定义为：Trace={Trace1,Trace2,…,Tracen}，Trace为可见时间窗口集合，Tracei∈Trace，指的是第i个可见时间窗口，i=1,2,3,…,n。Tracei={TIDi,Tsi,Tei,Tqi,Tdi,Tepi,TraSati,Prioi,TSi,Tyi,TeqUri}。属性对应的含义分别为：TID为可见时间窗口的ID，Ts为窗口开始时间，Te为窗口结束时间，Tq为所属圈号，Td为持续时长，Tep为所属设备，TraSat为所属卫星ID，Prio为优先级(根据设备与卫星的属性获得)，TS为使用状态(未分配、已分配)，Ty为圈次类型(升圈、降圈)，TeqUr为当前设备的利用率。

2.2 约束模型

在多星测控资源调度过程中要考虑的约束具体如下：

1)设备一旦跟踪一颗卫星，即要跟踪到设备对该卫星的本段可见时间窗口结束。

2)设备同一时间只能跟踪一颗卫星。

3)每个测控任务(可拆分任务根据约束完成拆分)只能选择一个可见时间弧段执行。

4)遥测任务与遥控任务可并行执行。

5)测控设备需与被测控的卫星频段相符。

6)同一卫星上不同任务执行需有一定的时间间隔，间隔时间由卫星自己的特性决定。

7)设备执行不同卫星的测控任务时，其间隔时间大于或等于测控设备切换时间。

多星测控资源调度的目标为充分利用有限的测控资源满足卫星测控需求，使得卫星、地面站都发挥最大的应用效能。基于上述约束和假定，该问题目标用公式描述如下：

max[αTaskR+(1-α)EquipR]

(1)

(2)

(3)

(4)

Taskl∈Satellitep-Taskl+1∈Satellitep≥β

(5)

TaTyi∩EqServcek≠Ø

(6)

SFp∩DFk≠Ø

(7)

[Tasi,Taei]∩[Tsj,Tej]≥TaDi+EqStk

(8)

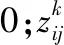
3 基于DNN的测控资源调度算法实现

DNN也叫多层感知机，其经典结构如图1所示，按层的类型划分为3类，即输入层、隐含层及输出层。其中第一层为输入层，神经元的个数即为提取的特征值的个数；最后一层为输出层，神经元的个数为输出的结果个数，可以为一个，也可以是多个；除此之外均为隐含层，隐含层的层数和隐含层神经元的个数可调，由结果的精度决定。

图1 DNN结构Fig.1 DNN structure

本节主要描述基于DNN的多星测控调度算法，其核心是对多星测控调度问题的DNN建模。首先根据对多星测控调度问题的实体建模与约束建模，选择出对调度结果有重大影响的特征值，使用合适的抽取方法对特征值进行离散化处理，即为DNN的输入。通过对DNN结构的分析可知，DNN的输入节点是相互独立的；对抽取的特征进一步分析可知，部分特征可以通过基于简单规则的预处理进行匹配性判定，因此提出了特征降维算法，对DNN模型进一步优化，缩减其输入节点数和求解空间，降低训练难度，提高算法精度。最后完成DNN模型的建立并对该模型进行训练，以得到可以精确预测调度结果的DNN模型。

3.1 特征值选择与抽取

DNN的输入神经元是相互独立的离散值，为适应其输入要求，将多星测控调度过程中约束进行抽取并进行离散化处理。结合第二部分的实体模型以及调度过程中的各种约束，提取出7个特征值，具体如下：

1)根据弧段有效时长是否大于或等于任务时长定义时间长度约束标记位D，弧段有效时长大于或等于任务时长时D为1，小于时为0。

2)根据任务所属卫星和弧段所属卫星是否匹配，定义卫星匹配标记位S，匹配为1，不匹配为0。

3)根据任务可选设备和弧段所属设备是否匹配，定义任务可选设备与弧段所属设备匹配标记位E，匹配为1，不匹配为0。

4)根据任务的类型(遥测、遥控、注入、测轨)和设备服务能力是否匹配，定义任务需求与设备服务能力匹配标记位C，匹配为1，不匹配为0。

5)根据任务、弧段、卫星优先级约束，定义优先级标记位P，取值为卫星、测控设备、任务的优先级之和。

6)根据可见时间弧段所在设备的利用率是否不小于等于80%，定义设备利用率标记位R，大于或等于80%时为1，小于为0。

7)根据资源调度的过程中是否出现冲突，定义冲突标记位U，冲突为1，不冲突为0。

3.2 特征降维算法

通过对上述DNN的描述与特征值的抽取可知，使用DNN解决多星测控调度问题的求解空间非常大，为测控任务与测控资源的全匹配。对抽取的特征值进行了深入的分析，发现其中有些特征值，如时间长度标记位、卫星匹配标记位、设备匹配标记位等，相互独立，特征符合性可以通过简单的计算、比较或者匹配完成，无需通过大量数据对DNN训练，进而学习规则解决。通过该预处理为测控任务初步匹配可能的测控资源，可以去掉无效的测控资源，大大缩减求解空间。同时，可将算法的特征值从7个缩减为3个，即：优先级标记位、冲突标记位、可见时间窗口所在设备的利用率。特征降维后，DNN的节点减少，学习难度减低，算法精度将随之提高。DNN特征降维算法(DNN feature dimensionality reduction algorithm，DNNFDRA)的具体过程如下：

Input: 卫星集合Satellite, 设备集合Equipment，可见时间窗口集合Trace，任务集合Task，用户偏好UP

Output: 任务与满足任务约束的所有可能的可见时间窗口的二元组集合DS〈Taski,Tracej〉

Begin

For每个测控任务Taskido

根据任务所属卫星TaSat获取卫星的频段SF，以及卫星的设备偏好SDS；

该任务的有效设备VaEqi=SDS∩UID∩Equipment；

过滤掉VaEqi中与SF频段不匹配的设备；

过滤掉与服务能力与任务类型TaTy不匹配的设备，获取有效设备集合EQ；

获取EQ中在[Tas,Tae]中的可见时间窗口Tracei；

ForTracei中的每个可见时间窗口TCj

任务所属卫星TaSat与可见时间窗口的卫星满足：TraSat: TaSat∩TraSat≠Ø；

比较任务时长与弧段有效时长满足:TaD≤[Tas,Tae]∩[Ts,Te]；

将满足上述比较条件的弧段与Taski组成二元组存入DS；

EndFor

EndFor

Return (DS)

End

DNNFDRA算法将不符合条件的可见时间窗口过滤掉，包括与任务所属卫星不匹配、不满足任务时长、不在有效设备集合中、任务类型与设备不匹配及任务所属卫星频段不满足的时间窗口。将过滤后符合条件的可见时间窗口与测控任务组成二元组集合。

根据DNN的输入特性，对获取的二元组集合进行处理，抽取优先级标记位、冲突标记位、测控设备资源利用率这3个特征值作为DNN模型的输入，降低了输入神经元的纬度，缩小求解空间，同时降低了DNN模型的训练难度。

3.3 DNN建模及训练过程

本文采用DNN经典的5层结构模型解决多星测控资源调度问题，包括输入层，3层隐含层以及输出层。输入层神经元即为抽取的特征值，输出层神经元为DNN计算结果。

DNN的本质是多元线性回归，可预测新输入数据的输出，可以将其看做是一个复杂函数，输入集为求解空间，输出即为预测结果，函数的系数等参数便是DNN网络结构。为获取预测效果较好的网络结构，需通过大量、高质量、多特征的训练数据有针对性的训练。训练数据由历史测控调度数据处理后得到：手动去掉调度失败的任务，使得测控任务的调度率为100%。其DNN训练流程如图2所示。为达到训练目标，DNN使用损失函数度量训练数据的输出损失，然后对损失函数优化求极小值，最终获得的线性系数矩阵W和偏移向量b即为DNN模型，求解过程一般使用梯度下降法迭代完成，当达到最大迭代次数或者停止迭代的阈值时停止。

图2 DNN训练流程Fig.2 DNN training flowchart

4 试验及结果分析

本文结合目前空间卫星分布情况和中国陆基测控站布局情况对算法进行验证。通过对比传统调度方法(TA)与DNN调度方法的性能，验证DNN的效能。其中，这里的传统调度方法是目前应用较广的基于资源综合加权优先级的调度方法[17]。通过比较DNN调度方法与传统方法(TA)的任务满足度与资源利用率，验证DNN算法的可行性及有效性；通过比较基于DNN的多星资源测控调度方法(MSTCS)和基于降维预处理的DNN调度方法(MSTCS_DF)的调度时间验证MSTCS_DF的效能。

4.1 试验场景

利用STK软件模拟100颗真实运行中的高中低轨卫星，其中中低轨卫星由全球星系统和铱星系统中的卫星组成，高轨卫星由北斗卫星组成；模拟中国陆基测控站中喀什站、渭南站、基律纳站等15套地面站测控设备，每颗卫星的测控任务为每天升圈测2圈次，降圈测2圈次，模拟未来测控网管理系统面临的“星多站少”的供求关系。

试验过程中准备了5组7天的任务数据，分别针对MSTCS、MSTCS_DF和TA方法进行测试。

4.2 试验结果及分析

使用上述试验数据，根据图2对DNN模型进行训练。使用DNN经典结构，即1个输入层，3个隐含层，1个输出层，每层具体的神经元个数以及激活函数如表1所示。

表1 DNN模型的层数、神经元数以及激活函数

对训练好的DNN，用5组7天的测控数据对多星测控任务分配资源，通过计算测控任务的加权满足度、资源加权平均利用率、算法运行时间3个方面对提出的算法进行结果分析，测试结果的平均值如表2和图3所示。

从表2与图3中可以看出，在任务满足度与资源利用率方面，DNN算法与传统算法TA性能都很好，且MSTCS_DF更为优越，说明使用DNN解决多星测控资源调度是可行且有效的。在调度时间方面，降维后的MSTCS_DF算法用时约缩减为MSTCS算法用时的17%，是传统算法用时的70%，说明MSTCS_DF算法具有高效性。

表2 测控数据的测试结果

图3 DNN测控数据的测试结果Fig.3 Test result of TT&C data

下面从优先级与资源分配的关系方面分析DNN算法(包括MSTCS算法和MSTCS_DF算法)的调度结果。图4(a)为可见时间窗口的优先级值与资源分配的关系，可以看出，可见窗口的优先级值越高，资源被分配的几率也越高；图4(b)为测控任务的优先级值与资源分配的概率，可以看出，任务优先级值越高，其被分配资源的概率也越高。综上可得，该调度结果符合一般调度的分配规律，DNN学习效果较好。

图4 优先级与资源分配的关系Fig.4 The relationship between priority and resource allocation

综上可以看出，DNN方法适用于解决大规模多星测控调度任务，且在性能上更优越，说明DNN方法在处理多星测控资源调度方面适应和扩展性良好。

5 结论

多星测控调度问题是复杂多约束、高冲突的NP组合优化问题，计算复杂度高，强度大，已有算法对多星测控调度适应性较差。本文分析了航天测控资源调度问题的特点和工程需求，针对问题求解中涉及的资源、测控任务以及约束，建立了DNN模型，并通过对测控任务初步资源分配，减少了算法的输入规模和输入特征的维度。然后通过大量历史数据的迭代训练获得DNN模型参数。最后用STK模拟真实应用场景，并通过大量试验验证了算法的高效性。此算法提高了测控任务的资源分配速率、效率以及满足度，且具有良好的适应性，能充分适应不同类型、规模的卫星测控任务资源分配问题。

为进一步提高多星测控调度的精度，下一步将深入分析影响多星测控调度的影响因子以及影响因子的优先级值，同时优化DNN的训练过程，考虑使用遗传算法或者模拟退火算法训练神经网络。