极低频超大型航天器姿态机动与物理试验验证

袁泉，林瀚峥，张军,*，魏春岭

1. 北京控制工程研究所, 北京 100190 2. 空间智能控制技术国家级重点实验室，北京 100190

1 引言

航天器姿态机动是指从某个飞行姿态向目标飞行姿态的调整过程，如轨道升高或降低之前的姿态调整、对观测目标的切换等，均需要进行姿态机动。

姿态机动控制需要在期望的时间范围内到达期望的姿态角和角速度，保证固定的时间点之后平台载荷能正常工作。姿态机动需要重点解决的是机动过程中的挠性振动抑制问题，这一点对于大型或超大型航天器来讲尤其突出[1-2]。普通航天器的挠性附件频率一般在0.2～1 Hz量级，对于极低频的超大型航天器，如中国空间站采用大型机械臂进行舱段的转位控制，机械臂两端连接的舱体质量超过20 t，整个系统呈“扁担”状态，系统频率极低，达到0.01 Hz量级，在此背景下如何实现系统的大角度姿态机动对控制系统的设计带来了巨大挑战。

目前国内外学者研究了各种方案试图解决航天器姿态机动过程中的挠性振动问题，在部分文献中通过多目标控制同时进行姿态控制与挠性振动抑制控制[3-4]，比较实用可行的方法是进行机动的路径规划，国内外的学者也提出了各种机动路径规划方法，主要包括：Bang-Bang规划法、多项式规划法、正弦规划法等[5-7]；文献[8]提出采用粒子种群方法进行轨迹规划，但计算量较大；本文作者提出了滤波轨迹规划方法[9]。到目前为止，挠性航天器姿态机动过程中的振动抑制问题仍然是航天控制领域中的一项研究热点。

但上述各种方法用于实际对象时控制性能上的差别没有明确结论，特别是应用于具有极低频主模态的超大型航天器时控制效果还没有正式评价。

本文针对0.01 Hz量级极低频超大型航天器的姿态机动控制问题进行研究，分别采用Bang-Bang轨迹规划、滤波轨迹规划、传统的相平面控制，以及不同的执行机构，包括喷气发动机和控制力矩陀螺(control momentum gyro, CMG)，构建了5种控制方案：姿态跟踪控制+Bang-Bang轨迹规划+喷气发动机、姿态跟踪控制+滤波轨迹规划+喷气发动机、姿态跟踪控制+Bang-Bang轨迹规划+控制力矩陀螺、姿态跟踪控制+滤波轨迹规划+控制力矩陀螺、相平面控制+偏置角速度规划+喷气发动机。最后构建0.01 Hz主振动频率的极低频超大型航天器机动试验系统，对上述5种控制方案的效果进行了比较，得出了有益的结论，为极低频超大型航天器在轨姿态机动提供参考。

2 系统动力学模型

考虑一个中心刚体带n个挠性附件的航天器，对挠性附件进行有限元模态分析，第j个挠性附件的模态坐标可表示为ηj=(ηj1ηj2…ηjl)T。

星体的姿态动力学方程可表示为[11]：

(1)

式中：Js为整星相对于质心的转动惯量；ωb为星体的姿态角速度，上标“×”代表相应三维列阵的反对称斜方阵；Abaj为从附件坐标系到本体坐标系的转换矩阵；Hj为星体中心体与挠性附件j的耦合矩阵；Il为l×l的单位阵；Cj为附件j的阻尼阵；Kj为附件j的刚度阵；Torq为作用于星体的控制力矩。

3 姿态控制算法

3.1 姿态跟踪控制算法

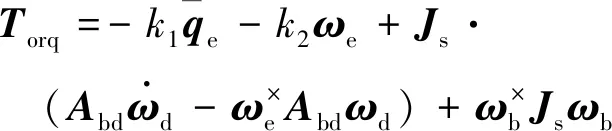
(2)

式中：k1，k2为正的常值。

ωb=ωe+Abdωd

本文重点在于对姿态机动问题的研究，在此不对控制器的设计展开分析，该控制器的稳定性证明可见文献[11]。

3.2 轨迹规划方法

(1)Bang-Bang轨迹规划方法

Bang-Bang轨迹规划方法常用于中小型航天器姿态机动时的轨迹规划，不关注机动过程中的挠性振动问题，其原理框图如图 1所示。

图1 Bang-Bang轨迹规划方法控制框图Fig.1 Illustration of Bang-Bang control method

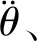
图2 Bang-Bang机动过程规划方案Fig.2 Illustration of Bang-Bang maneuver scheme

(2)滤波轨迹规划方法

指令滤波设计方法的框图如图 3所示。

图3 指令滤波设计方法控制框图Fig.3 Illustration of command filter method

其基本思路是在Bang-Bang轨迹规划的基础上，将Bang-Bang轨迹规划出来的角加速度、角速度、姿态均进行再滤波，以实现对挠性附件的振动抑制。本文中，对G(s)设计为如下形式的滤波器：

式中：ωz为滤波器零点的频率；ωp为滤波器极点的频率；ξz为滤波器零点的阻尼；ξp为滤波器极点的阻尼。上述滤波器的参数设计方法可完全参考惯用的结构滤波器设计方法，文献[12]专门给出了结构滤波器的设计方法，在这里不详细介绍，一般设计成低通滤波器、陷阱滤波器。

采用上述滤波器后，对机动目标姿态的可达性证明见文献[9]。

3.3 相平面控制算法

相平面控制算法一般采用姿态为横轴、姿态角速度为纵轴，将姿态-姿态角速度平面划分为多个子区域，在子区域内规划喷气发动机的喷气时间，实现姿态-姿态角速度相曲线向原点的收敛，本文中采用的相平面算法见文献[13]。传统的相平面控制方法主要用于姿态稳定，其输入为星体的姿态与姿态角速度，输出为喷气脉宽，本文针对大角度姿态机动，进行如下改进，用相对目标角速度的姿态角速度误差代替传统的姿态角速度作为相平面控制的输入，即：

(3)

3.4 执行机构的选取

第3.1小节、3.3小节给出了姿态机动的控制指令，只要利用执行机构输出式(2)中的控制力矩，就能够实现对第3.2小节中期望轨迹的跟踪。执行机构可以选用喷气发动机或CMG，前者只能输出固定大小力的脉宽，输出不同的控制力矩时，需要利用脉宽调制技术，实现控制性能上的等价；如果采用CMG作为执行机构，由于CMG能输出变幅值的控制力矩，因此需要设计CMG的操纵律，给出单只CMG的框架角速度指令。脉宽调制技术、CMG的操纵律设计均具有丰富的内容，不是本文的重点，本文采用喷气发动机作为执行机构时，采用文献[14]中的脉宽调制方法进行脉宽调制，采用CMG作为执行机构时，采用文献[15]中的CMG操纵律。

4 试验验证

4.1试验系统

针对采用机械臂进行空间站组装的极低频超大型航天器机动控制，构建系统试验，系统原理如图 4所示。本次试验中，采用一个单自由度气浮台模拟超大型航天器的单轴机动，采用两个三自由度台模拟超大型航天器的在轨组装舱段，其中一个三自由度与单自由度气浮台通过桁架连接，形成组合体，另一个三自由度台通过一个10 m的钢质细杆连接，两个三自由度台的质量均为1 t，10 m钢质杆连接后形成的组合体，经测试其第一阶主振动频率为0.01 Hz，用于模拟超大型航天器的极低频振动模态，整个系统惯量约200 000 kg·m2。

图4 极低频超大型航天器机动试验系统原理Fig.4 Illustration of physical testbed of ultra large spacecraft with low frequency

该系统也是目前为止国内构建的最大惯量的航天器物理试验系统，可以实现极低频条件下超大型航天器的姿态机动控制试验。

对于指定的控制力矩，采用两种执行机构实现，一种为输出力矩为150 N·m的冷气推进系统，一种为采用2只1 500 N·m·s的CMG，采用平行构型安装。

为了检测机动过程中，极低频挠性附件的变形量，在其中一个三自由度台安装激光测振仪，对10 m长度机械臂连接的三自由度台的变形量进行实时测量。

在本试验中，考虑到大理石平台与气浮台的相对安装关系，所有的机动角度均设为45°，整个机动过程持续100 s，分解为：30 s(加速)+40 s(匀速)+30 s(减速)，如图 5所示。

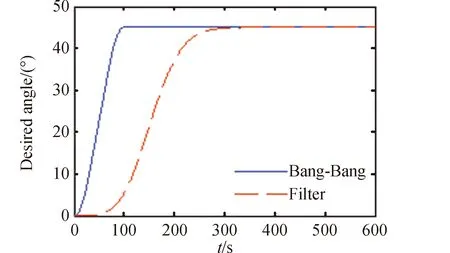
图5 机动期望姿态角Fig.5 Desired maneuver angle

各个控制方案的姿态机动角、角速度分别如图6、图7所示，挠性形变如图8所示。控制方案1、2、5机动过程中喷气脉宽如图9所示，控制方案3、4机动过程中控制力矩如图10所示。

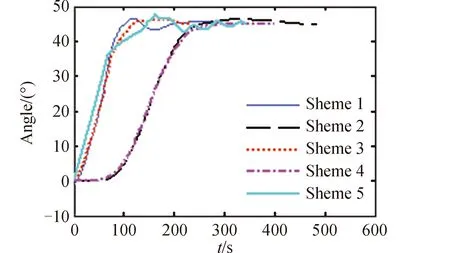
图6 机动姿态角Fig.6 Actual maneuver angle

图7 机动姿态角速度Fig.7 Actual maneuver angle velocity

图8 机动过程中挠性形变Fig.8 Flexible deformation during attitude maneuver

图9 控制方案1、2、5的机动过程中喷气脉宽Fig.9 Jet command during attitude maneuver of control scheme 1, 2 and 5

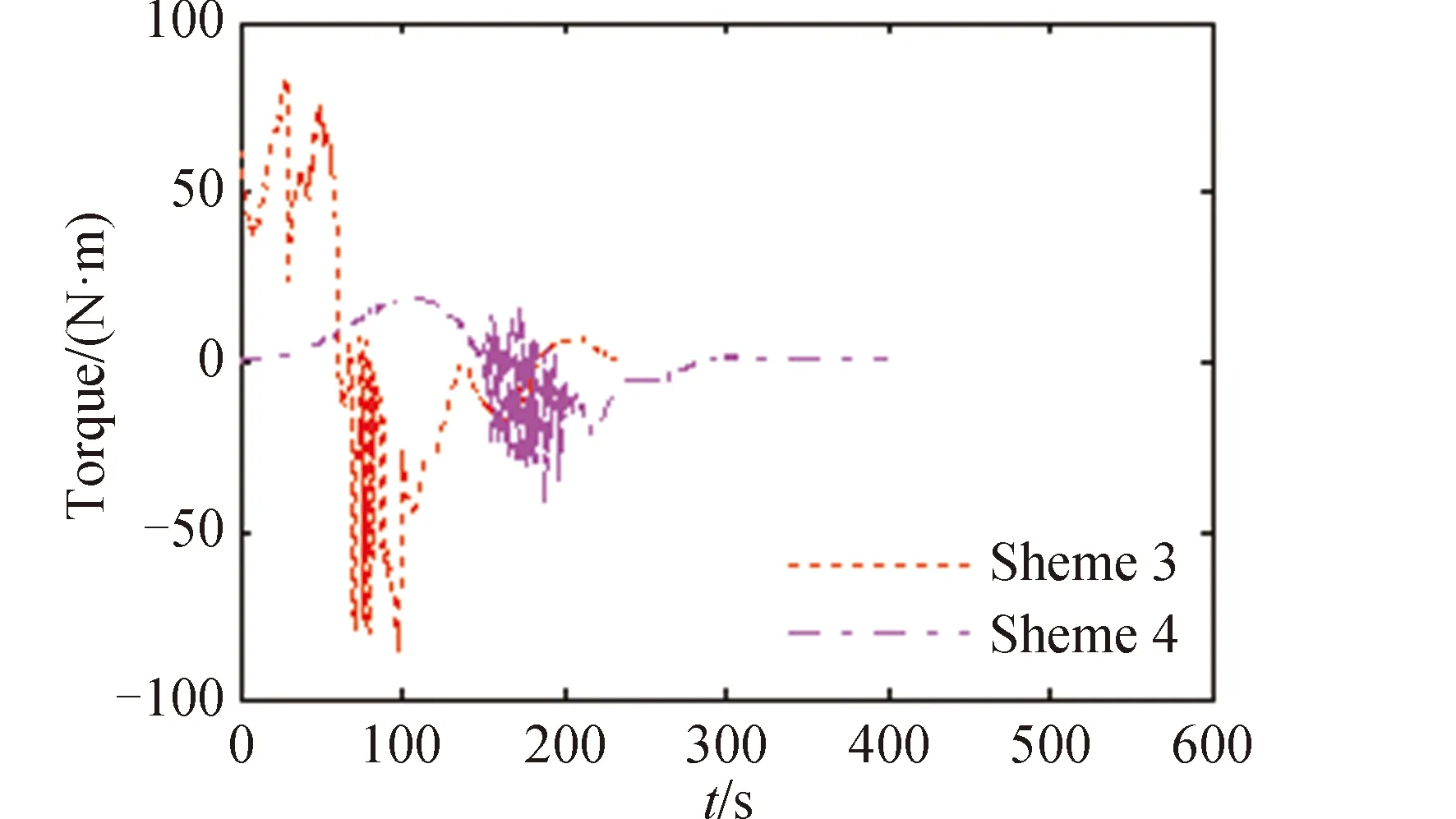
图10 控制方案3、4的机动过程中的控制力矩Fig.10 Control torque during attitude maneuver of control scheme 3 and 4

4.2 控制方案1：姿态跟踪+Bang-Bang轨迹+喷气

控制方案1采用姿态跟踪控制器，采用喷气发动机对控制力矩进行脉宽调制，采用Bang-Bang轨迹规划，可以看到，约230 s左右，姿态机动到位并停止振动。机动过程中最大挠性变形约0.9 m。

4.3 控制方案2：姿态跟踪+滤波轨迹+喷气

控制方案2与控制方案1的区别是轨迹规划方法采用滤波方法，即利用滤波器对机动的路径进行滤波，以期对挠性附件的振动进行抑制。

可以看到，机动过程持续时间约250 s后到位，整个机动过程中挠性变形最大为0.25 m。

4.4 控制方案3：姿态跟踪+Bang-Bang轨迹+CMG控制

控制方案3与控制方案1的区别是将执行机构换成CMG，但仍然采用Bang-Bang轨迹规划方法，这样其输出力矩为连续控制力矩。机动过程中挠变形量达到了0.85 m。可以看到，执行机构采用CMGs后，虽然能够输出连续力矩，但挠性变形量并没有明显减小。

4.5 控制方案4：姿态跟踪+滤波轨迹+CMG控制

控制方案4是在控制方案3的基础上，采用滤波轨迹规划方法，同时还采用CMG作为执行机构进行姿态跟踪控制，通过试验可以看到，约250 s完成了姿态机动，而机动过程中最大挠性变形量只有约0.2 m。将机动路径采用滤波轨迹规划后，挠形变形得到了明显抑制。

4.6 控制方案5：相平面+偏置角速度+喷气

4.7 各控制方案试验总结与机理分析

通过上面试验可以看到，各种控制方案下，机动到位的时间均在200～250 s，但将上述各控制方案的最大机动角速度、0.01 Hz挠性结构的振动变形量进行统计，如表 1所示，各种控制方案下相差较大。其中相平面控制方法，挠性变形量达到了1.1 m，而采用Bang-Bang轨迹规划方法，挠性变形量为0.9 m(执行机构为喷气发动机时)、0.85 m(执行机构为CMG时)，均超过采用滤波方法进行轨迹规划时的变量，变形量分别对应0.25 m(执行机构为喷气发动机时)、0.2 m(执行机构为CMG时)。

表1 5种试验控制方案机动角速度与变形比较Table 1 Comparison of different maneuver tests

从上述比较可以看到，对挠性变形影响最大的是机动时的轨迹，其影响超过了采用喷气发动机或者CMG作为执行机构。挠性变形量最小的情况为控制方案4，即采用姿态跟踪控制器+滤波轨迹规划+CMG，其变形量为最大的控制方案5的变形量的18.2%，减小了约81.8%。

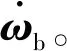
因此第二类控制方案优于第一类控制方案。

而相同的轨迹规划方法下，采用CMG方法，相对喷气控制方法，挠性振动更小，则可以理解为CMG是连续力矩输出机构，喷气是脉冲性执行机构，脉冲式执行机构的输出中包含的信号频率范围更高，不能严格输出控制器要求的指令，会对挠性振动带来大的冲击，因此控制方案4略优于控制方案2。

而相平面控制，相对其他两类方案，类似于切换控制，存在正反两个方向不断喷气控制的现象，因此挠性振动最明显，相平面控制一般主要应用于刚性航天器的控制，或挠性振动影响不大的航天器的控制，因此对挠性振动影响比较大的航天器一般不采用该控制方案，本文的试验结果也验证了这一结论。

5 结论

针对具有0.01 Hz极低频主振动模态的超大型航天器的姿态机动控制，基于Bang-Bang轨迹规划、滤波轨迹规划，以及传统的相平面控制方法，本文给出了5种姿态机动控制方案，并构建了20×105kg·m2量级惯量的超大型地面物理试验系统，对不同控制方法进行了试验。试验结果表明，对挠性变形影响最大的是机动轨迹，其影响超过了采用的执行机构是喷气发动机或控制力矩陀螺，同样的控制算法和执行机构下，采用滤波轨迹规划方法，其挠性变形比Bang-Bang轨迹规划方法能减少40%～50%；但采用不同的执行机构，在相同的轨迹规划方法下，挠性变形量相差约6.25%～12.5%，采用姿态跟踪控制+滤波轨迹规划方法+控制力矩陀螺的方案变形量最小，其挠性变形量比传统的相平面控制方法能减少81.8%。