异形光斑的高精度光束偏转角度测量
2022-02-22邹炎升张乃元袁辉刘陈刘德明
邹炎升,张乃元,袁辉,刘陈,刘德明
华中科技大学 光学与电子信息学院,武汉 430074
1 引言
空间光通信的通信容量大、通信速率高、传输距离远、保密性好,极大地弥补了卫星微波通信的不足,是微波通信的潜在补充手段[1]。由于激光通信具有信号光束窄,发散角小的特点,因此在进行和保持通信链路信息的传输时必须保持两终端接收机之间在一定允许误差范围内的光轴对准[2]。对入射光束相对目标飞行器光轴的角度进行精确测量是实现激光链路捕获跟踪的前提与关键,直接决定了通信终端之间的对准精度,进而影响天线的光接收效率[3-4]。在近地空间,激光光束的波前受大气湍流的影响而变化,造成接收端探测器收到的光斑多为能量分布不规则的异形光斑[5],而且,光斑形状由于大气扰动随时间变化而发生改变。为保障空间激光通信的可靠性和通信能力,对光斑异形情况下的光束偏转进行高精度测量必不可少。
目前,空间光通信多采用响应速度快、角度分辨率高的四象限探测器(QD)作为精跟踪探测器[6-7],采用电荷耦合元件(CCD)、作为粗跟踪探测器。QD不能获得光斑的形状信息,适合于规则光斑情形下的光束偏转角度测量,实际应用时通常将光斑形状视作均匀光斑和高斯光斑进行处理[8-10]。QD测角精度受光斑形状及光强分布的影响较大,当光斑为异形光斑时测量误差较大,而CCD则几乎不受光斑形状及光强分布的影响[11]。
本文基于空间激光通信终端中的粗跟踪探测器CCD和精跟踪探测器QD,提出一种多源信息融合算法,通过对QD及CCD的数据信息融合,使得低分辨率CCD获取的光斑形状信息能够与QD高精度角度测量能力互为补充,在保持QD高分辨率和高响应速度的同时,提高QD对不规则光斑偏转角的测量精度。
2 多源信息融合算法
对于均匀光斑或高斯光斑,当光斑质心位于四象限探测器中心附近时,QD常常使用中心近似法进行光斑位置测量,此时,光斑实际位置和QD测量值之间近似呈现线性关系[12-13],可以表示为:

(1)
式中:σx=[(IA+ID)-(IB+IC)]/(IA+IB+IC+ID),σy=[(IA+IB)-(IC+ID)]/(IA+IB+IC+ID);x0、y0为光斑的实际位置坐标;IA、IB、IC、ID为QD四个象限所测得的阻抗电流;k为比例系数,由光斑能量分布、光斑半径及QD的半径共同决定。
对于空间激光通信,激光束在传输过程中受大气湍流的影响,畸变为不规则的异形光斑,不能使用传统的中心近似法进行计算,否则将产生较大的测量误差。针对此问题,对式(1)进行修正:

(2)
式中:kx、ky分别为X、Y方向的比例系数,由光斑形状决定;ΔGx和ΔGy为中心测量误差。上述参数通过CCD图像和QD共同作用获得。
2.1 比例系数k的修正
对于不同形状不同能量分布的光斑,其k参数的计算公式是不同的;即使对于同一种规则光斑,也需要得到具体的光斑半径参数,但半径参数仅通过QD是无法确定的,这些因素无疑限制了传统计算公式的应用。
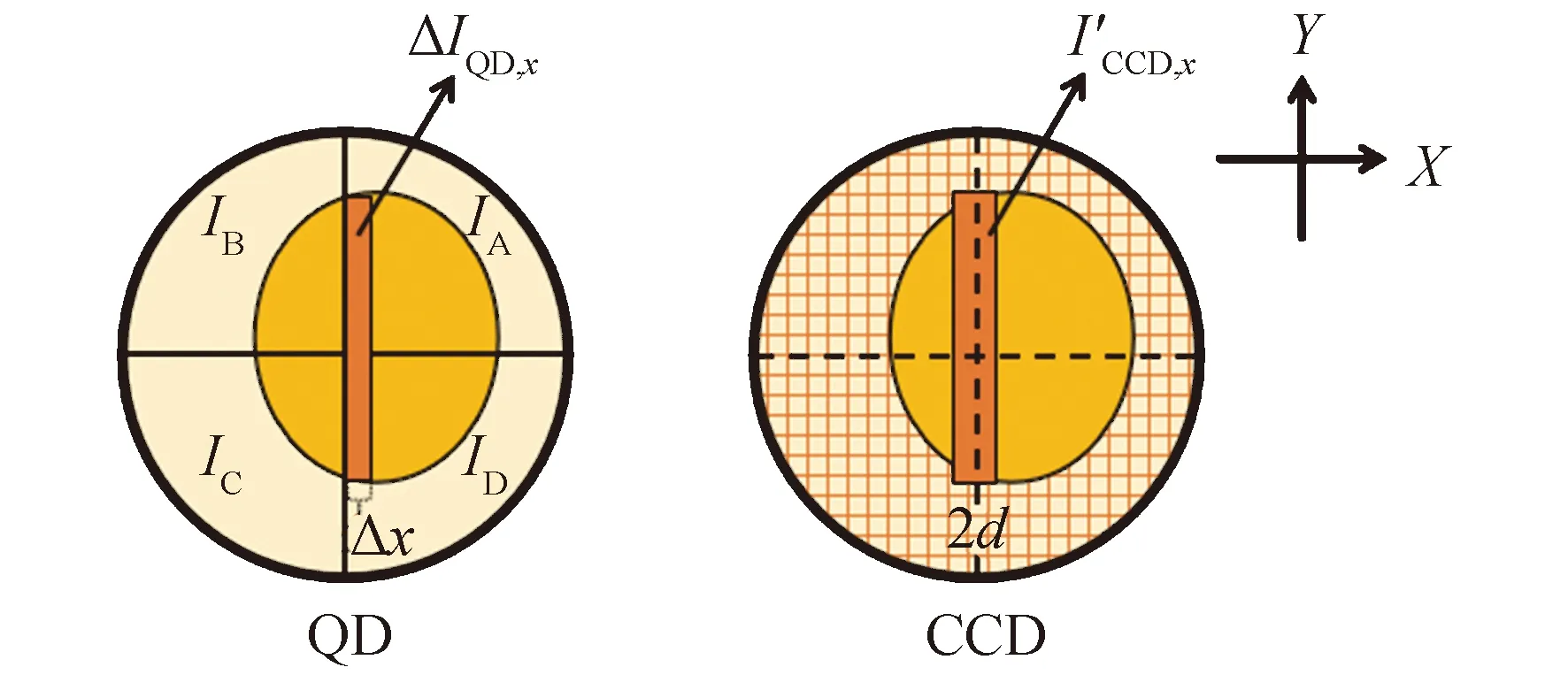
图1 QD数据与CCD图像融合测角原理图Fig.1 Schematic diagram of angle measurement with both QD data and CCD image
当光斑中心在QD上的位置改变时,光敏面各象限上的光斑面积也会改变,从而引起四象限探测器各象限输出电流强度的变化[14]。以X轴方向位置偏移为例,光斑沿X轴方向移动一段位移Δx,一、四(或二、三)象限电流之和IA+ID(或IB+IC)对应改变量为ΔIQD,x。对于空间光通信应用,对光束偏转进行实时检测,光斑位置的改变量Δx很小,则ΔIQD,x可以表示为:
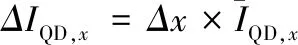
(3)
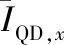
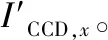
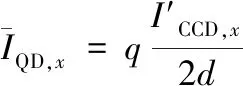
(4)
式中:d为CCD单个像素的宽度。考虑到CCD与QD的光电响应度不同,引入QD探测面总电流与CCD探测面总电流的比值系数q=IQD/ICCD,IQD和ICCD分别为QD探测面总电流与CCD探测面总电流,且IQD=IA+IB+IC+ID。
同时,光斑移动导致IQD×Δσx=2ΔIQD,x,Δσx为光斑移动时σx的变化量。结合式(3)、(4)可得到:
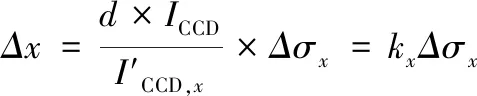
(5)

2.2 中心测量误差ΔG的引入
由式(1)可以看出,对于QD常用的中心近似法,当光斑所在位置使得QD输出的X,Y方向的解算值为零(σx=σy=0)时,QD的中心便是光斑中心,即x0=y0=0。然而对于异形光斑,这种光斑中心测量方法并不合适,需要重新设计光斑中心测量方法并引入中心测量误差。
通常认为,当光斑的质心(光强分布的加权平均位置)与探测器中心对准时,可以获得最大的接收功率[16],所以可以选定质心作为光斑的中心。预先设定QD与CCD的中心G0重合,如图2所示,以G0为原点建立坐标系,定义QD采用传统算法得到的光斑中心坐标GQD(xG-QD,yG-QD),CCD计算得到的光斑质心坐标GCCD(xG-CCD,yG-CCD)。当光斑为均匀光斑或者高斯光斑时,QD测得的光斑中心GQD与CCD测得的质心GCCD重合。而当光斑为异形光斑时,GQD与GCCD不再重合,此时需引入中心测量误差对上述中心偏离进行修正:

图2 异形光斑的三个中心位置示意Fig.2 Schematic diagram of three central positions of irregular light spots
2.3 修正公式对一般光斑的适用性论证
(1)对均匀圆形光斑的适用性论证
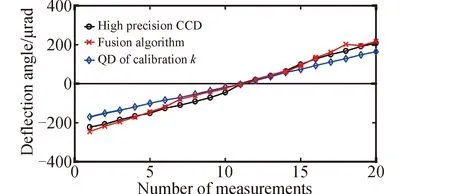
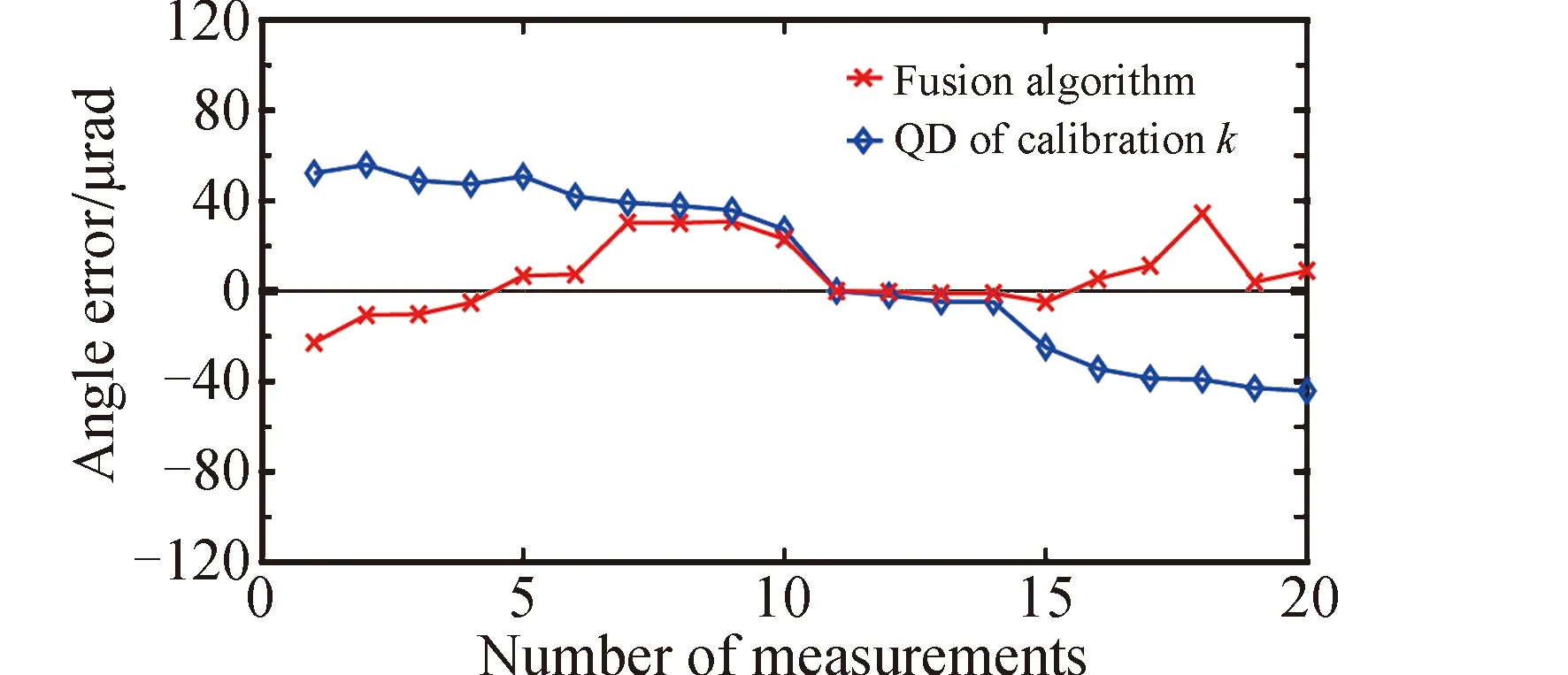
对于均匀圆形光斑,即各处光强相等的圆形光斑,当d< 式中:w为QD在总光斑面积上的电流均值。 代入式(4)、(5)可得: (6) 式(6)与中心近似法得到的结果相同[13],从而验证了修正公式对均匀圆形光斑的适用性。 (2)对高斯圆形光斑的适用性论证 对高斯圆形光斑,即光强分布为二维高斯分布的圆形光斑,当d<<ω,ω< 式中:I0为高斯光斑中心处的光强。 则有: 又ω< 最终得到: (7) 式(7)与中心近似法得到的结果相同[13],从而验证了修正公式对高斯圆形光斑的适用性。 图3 QD分段线性近似的响应曲线图Fig.3 Piecewise linear approximation response curve of QD 可根据响应曲线图反推出此时光斑沿X轴方向的绝对偏移量x0,进而算出X轴方向的绝对偏转角度,Y轴方向的绝对偏转角度同理可得。 由式(5)可以看出Δx等于Δσx与kx的乘积,系数kx在短时间内可认为保持不变,而Δσx是QD解算值的变化量,只与QD相关,所以融合算法的测角分辨率与响应速度仅由所使用的QD决定,融合算法可以保持QD的高分辨率与高响应速度。 对于异形光斑,常用的检测方法是高精度CCD质心法,即利用高精度CCD求得光斑质心的偏移量。下面对算法的计算复杂度进行比较分析。 图4 传统方法及融合算法对异形光斑进行模拟仿真的结果Fig.4 Simulation results with the conventional method and the multi-source information fusion method for the irregular light spot 由图4可以看出,相对于仅基于QD的传统中心近似算法,通过对QD数据与CCD图像进行数据融合,融合算法能够根据光斑形状调整比例系数k,从而显著提高非规则光斑的偏转角度测量准确性。 为了验证融合算法有效性和仿真分析结果的正确性,设计了如图5所示的实验验证系统。实验中,激光器出射波长为1 550 nm,出射功率约为1 mW。为保证高精度CCD测得的光斑位置数据更能代表准确值,透镜1采用焦距为500 mm的双胶合透镜,而高精度CCD(Ophir,SP928-1550)的分辨率为1 448 (行)×1 928 (列),单个像素的尺寸为3.69 μm×3.69 μm,可实现7.38 μrad角度分辨的测量。透镜2与透镜3均是焦距为100 mm的双胶合透镜,低精度CCD(滨松,C14041-10U)的分辨率320 (行)×256 (列),像素尺寸为20 μm×20 μm。QD则采用的是Thorlabs公司的PDQ30C,感光面直径3 mm,其波长测量范围为1 000 ~1 700 nm的红外(IR)范围,峰值响应度为1 A/W@1 630 nm。 图5 融合算法验证实验系统及低精度CCD测得的异形光斑示意Fig.5 Experimental setup for fusion algorithm verification and irregular light spot measured by low-precision CCD 在偏转镜前放置一个不规则玻璃器皿,使得光束经过此器皿后形成异形光斑。驱动偏转镜每次偏转10 μrad,偏转镜偏转20次,分别记录下高精度CCD与低精度CCD的图像以及QD的输出电流值。对获得的数据和图像采用仅QD传统算法、QD与CCD融合算法进行处理,采用高精度CCD质心算法得到结果作为准确值进行对比,结果如图6所示。 图6 三种不同方法所测得的光束偏转角曲线Fig.6 Curves of beam deflection angle measured by three different methods 其中,“高精度CCD”曲线是通过高精度CCD质心算法算得的光斑偏转角移动曲线,“融合算法”曲线是QD数据与低精度CCD图像通过融合算法得到的光斑偏转角移动曲线,“标定k的QD”曲线是取光斑为高斯光斑时标定得到的比例系数k所绘制的光斑偏转角移动曲线。实验过程中的数据处理方式与仿真过程一致。 以高精度CCD所测得的偏转角为准确值,得到其它两种方法的测量误差曲线,如图7所示。从图6、图7可以看出“融合算法”曲线法得到的光斑偏转角误差最小。由数据计算可得,对于标定k的QD算法均方根误差为37.74 μrad,而融合算法的均方根误差为16.77 μrad,相对于前者减少了55.56%。标定k的QD算法误差角度峰峰值为100.17 μrad,而融合算法的误差角度峰峰值为57.12 μrad,相对于前者减少了42.98%。这样也说明了,相对于传统的QD算法,QD与低精度CCD的融合算法所算得的光斑偏转角更接近准确值,从而验证了融合算法对异形光斑偏转角测量精度的有效提高。 图7 以高精度CCD为准确值时其余两种方法的测量误差曲线Fig.7 Error curve of the other two methods compared with that of high-precision CCD 本文提出了一种基于多源信息融合的高精度光束偏转角度测量方法。通过理论推导和实验验证可以得出以下结论: 1)该方法能够提高QD对异形光斑的角度偏转测量精度。相对于传统中心近似法,该方法对异形光斑偏转角的测量均方根误差改善了55.56%,测量误差峰峰值减少了42.98%。 2)该方法在提高测角精度的同时能够保持QD的高分辨率与高响应速度,且相比于高精度CCD质心法具有硬件要求低、运算复杂度低等优点。 3)该方法能够适应各种异形光斑以及规则光斑,对由于大气湍流导致光斑畸变的星-地/地-地激光通信具有应用优势。 本文实验验证了融合算法对形状不规则光斑在mrad范围的高精度偏转角度测量,后续将探讨如何降低CCD噪声及QD噪声,以进一步提高测量精度。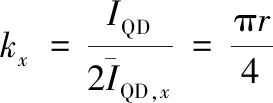

3 测量范围、分辨率与复杂度分析
3.1 融合算法测量范围适用性
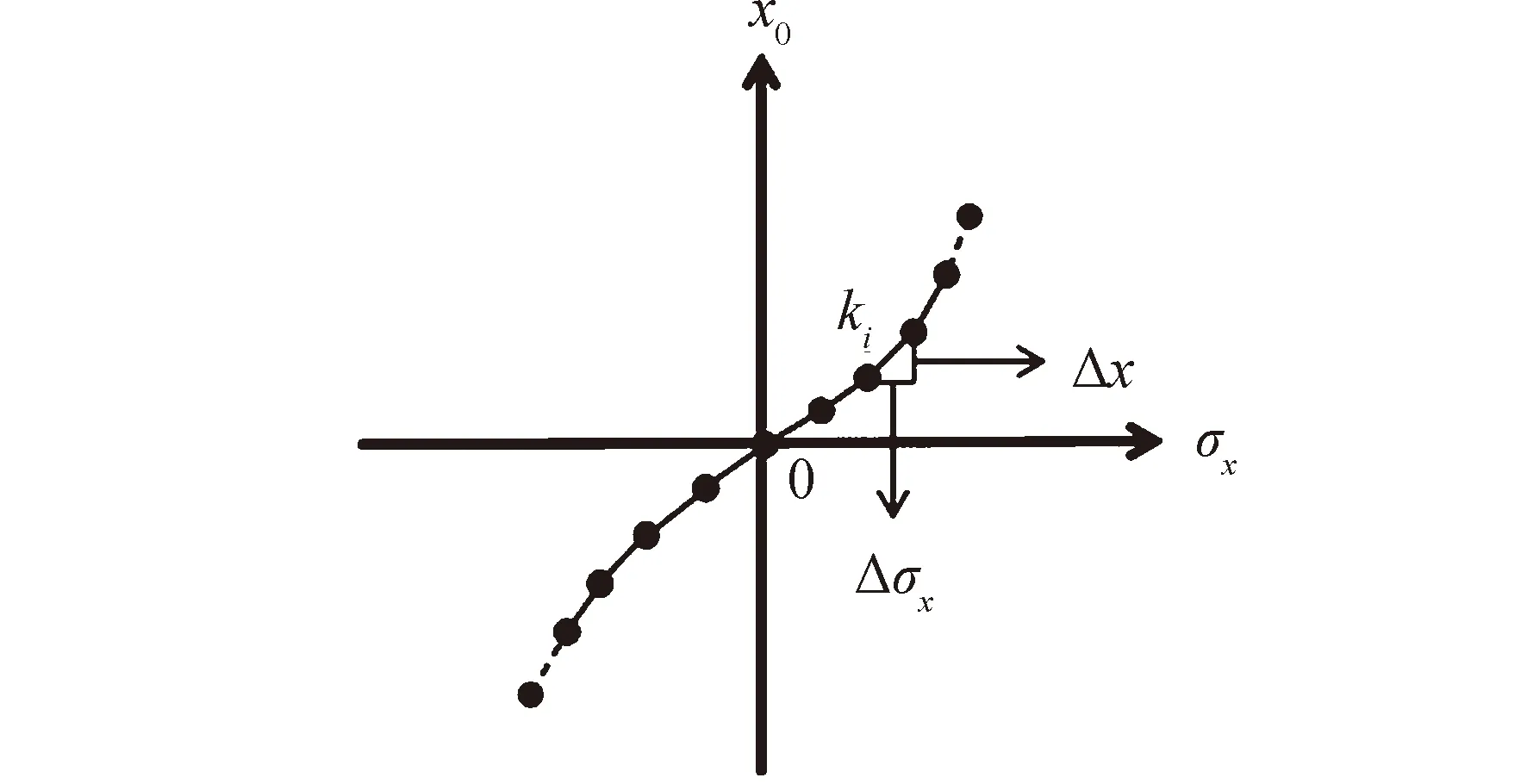

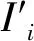
3.2 融合算法分辨率分析
3.3 融合算法运算复杂度分析

4 仿真校检与实验验证
4.1 异形光斑模拟仿真
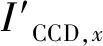

4.2 实验验证

5 结论
