基于覆盖圆的太阳同步回归轨道卫星目标轨迹调整方法
2022-02-22林竹翀王剑锋张蔚柳丽朱子亨魏银杉
林竹翀,王剑锋,张蔚,柳丽,朱子亨,魏银杉
北京市遥感信息研究所,北京 100192
1 引言
遥感卫星在环境监测、地理测绘等领域发挥着重要作用。遥感卫星通常采用太阳同步回归轨道,以保证稳定的光照条件、电量状态和地面重访性能。太阳同步回归轨道主要采用基于星下点轨迹漂移的维持方法,即通过调整轨道高度控制星下点轨迹相对标称轨迹的漂移范围,从而使卫星轨道按照设计的标称太阳同步回归轨道运行[1-5]。
为提高地面重访和全球覆盖效率,需要运行多颗卫星构成星座来实现。在卫星星座构型保持中,星座整体对地面目标的重访能力是星座构型维持的主要目标。此外,在有限的地面接收资源情况下如何避免接收站冲突,也是卫星轨道长期维持中需要考虑的问题。
当前主要通过维持星下点轨迹间隔均布的方法来维持星座构型,如高分一号、吉林一号、北京二号卫星等。该方法能有效提高星座整体的地面重访性能。但是对于成像分辨率或测绘精度要求较高的情况而言,卫星可侧视范围较小,此时星下点轨迹均布并不一定是星座整体对地重访性能最优解。
此外,对于不同降交点地方时卫星构成的星座,由于各星降交点地方时漂移速度存在差异[6-8],只对星间星下点轨迹分布进行保持可能导致星间相位(纬度幅角)过于接近,造成地面站数据接收冲突。为保持降交点地方时频繁进行轨道倾角调整,则会产生额外的燃料消耗[9]。
目前尚未有关于综合考虑卫星星座重访性能和星间相位的星座构型维持方法的相关文献。
太阳同步回归轨道卫星对地面重访能力与轨道回归特性密切相关。文献[10]首次将一个平太阳日内卫星绕地球圈数定义为Q值,并利用Q值研究了太阳同步回归轨道卫星在回归周期内的访问顺序。文献[11]论述了Q值的优化方法,认为基于Q值选取的轨道设计算法是从理论上设计太阳同步轨道的关键。文献[12]采用基本交点距的描述方法,将回归周期内轨道的访问顺序加以量化,将重访周期的确定问题转换为求解丢番图代数方程。以上研究为太阳同步回归轨道重访能力的分析优化提供了很好的方法基础,但是主要关注单颗卫星重访性能的分析优化。
本文利用基本交点距构建“覆盖圆”的概念,提出了基于覆盖圆的星座重访性能分析和目标轨迹调整方法,利用该方法进行星座构型维持可在同一个框架下同时考虑卫星相位保持和重访性能优化问题,可用于卫星星座设计和在轨卫星星座的性能调优。
2 基本概念与模型
本节阐述本文中用到的一些概念的定义。
定义1:标称轨迹。指太阳同步回归轨道卫星轨道维持的参考星下点轨迹。采用J2模型生成,由回归圈数、回归天数和初始降轨穿越赤道经度唯一确定。
定义2:目标轨迹。指轨道维持中,卫星某圈次(从升交点起至下一次经过升交点为一个圈次)计算降交点经度漂移量时参考的一圈标称轨迹。
定义3:摄影条带。回归圈数为R的卫星在一个回归周期中标称轨迹(降轨部分)将地球表面南北纬80°以内的区域分为R份。定义以标称轨迹为中心线、以相邻轨迹在东西方向的距离为东西宽度的R个条带为卫星摄影条带。以穿越赤道经度为L0的标称轨迹所处的摄影条带为1号条带,向西依次将所有条带进行编号。称目标轨迹所处的摄影条带编号为当前的条带号。
2.1 星间相位差表述方式
本文中卫星相位采用纬度幅角表示。纬度幅角通过计算卫星近地点幅角和真近点角之和得到。星间相位差为:
Δuab=ωa-ωb+fa-fb
(1)
式中:u,ω和f分别为纬度幅角、近地点幅角和真近点角,下标表示卫星代号。
由于卫星近地点幅角和真近点角不是轨道维持所关注的参数,式(1)不能体现轨道维持过程中卫星相位变化的规律。以下推导出用地面轨迹偏离、目标条带号和降交点地方时表示的卫星相位差公式,更有利于问题分析。
根据降交点地方时的定义,卫星a和卫星b相邻两次经过降交点的时间差为:
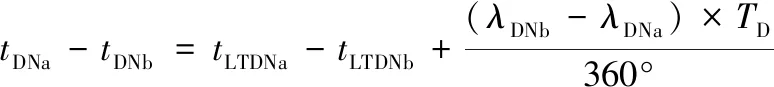
(2)
式中:tDN为卫星经过降交点的时间;tLTDN为降交点地方时;TD为一个平太阳日的时间长度;λDN为降交点经度。
降交点经度差可以用地面轨迹偏离和条带号来表示:
λDNb-λDNa=dλDNb-dλDNa+λb-λa=

(3)
式中:λa和λb为目标轨迹降交点经度;dλDN为实际轨迹降交点经度相对于目标轨迹的偏离量;R为回归圈数;A为该圈目标轨迹所处的条带号。
式(3)代入式(2),可得到以地面轨迹偏离、目标轨迹条带号、降交点地方时表示的卫星相位差:
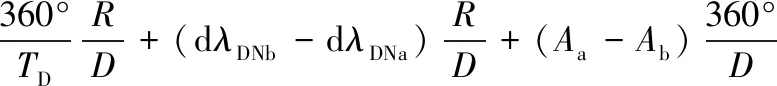
(4)
2.2 覆盖圆的构造
太阳同步回归轨道卫星标称轨迹由回归天数和回归圈数决定,其每天的分布具有如下规律(见图1):
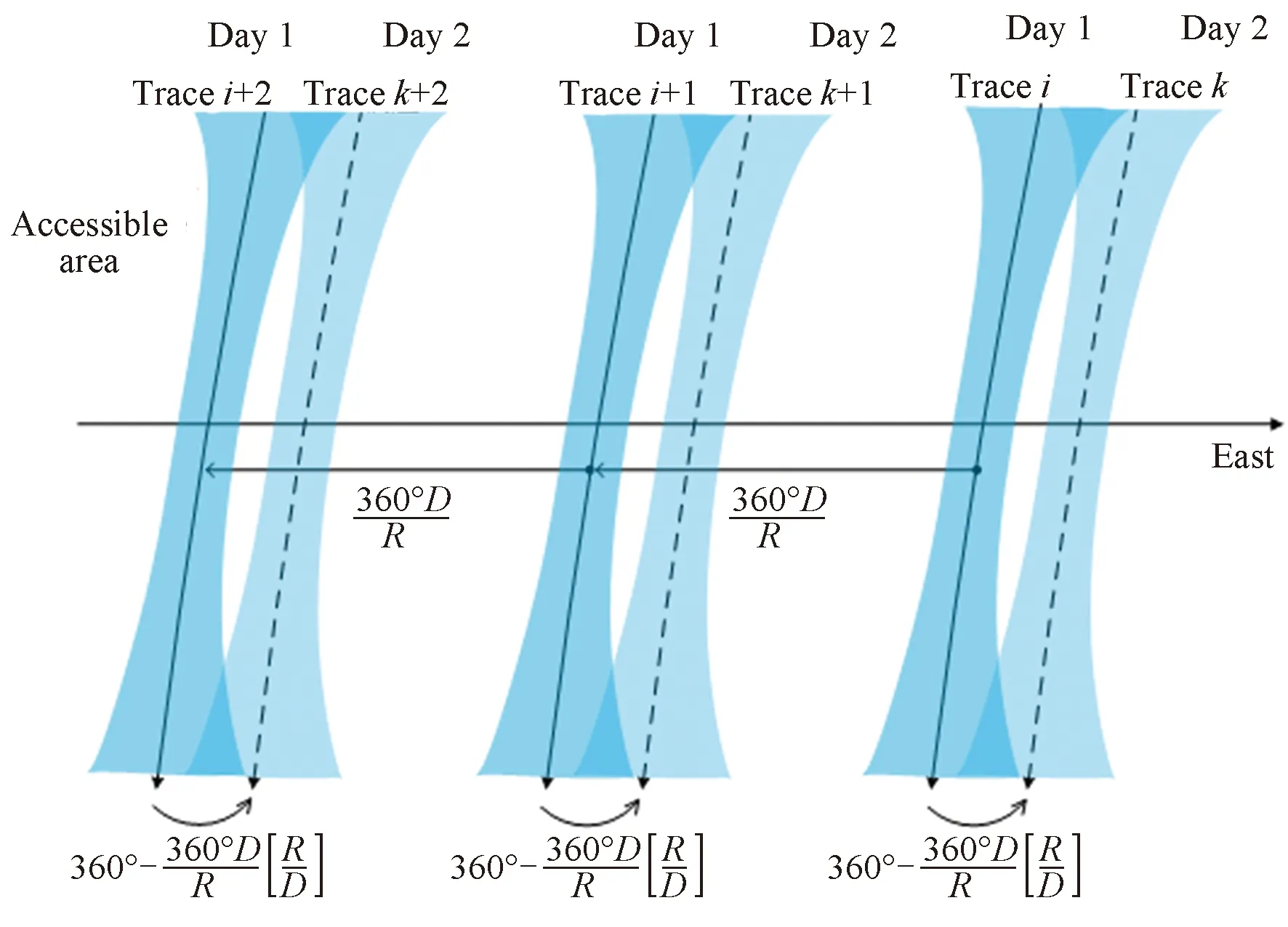
图1 卫星星下点轨迹分布及其变化规律示意Fig.1 The distribution and changing of satellite ground traces
3)相同回归特性的多颗太阳同步卫星遵循相同的跳变规律,并且星下点轨迹相对位置保持固定。
由于圆轨道卫星在相同纬度上每一轨覆盖区域的经度跨度是相同的[11-15],因此重访性能在东西方向上会以基本交点距为周期进行重复。通过研究目标所在纬度线上一段基本交点距的重访情况,可分析和优化星座整体对该目标的重访性能。为此,通过如下方法构造覆盖圆。
以目标纬度上地面某点为起点,向西将地面上各点以基本交点距为周期依次顺时针投影到一个抽象的圆上,称该圆为“覆盖圆”,如图2所示。

图2 目标纬度圈投影至覆盖圆示意Fig.2 Projection of target latitude circle to revisit-circle
目标点到覆盖圆上的投影公式为:

(5)
式中:θ为覆盖圆中对应点所处的角度,逆时针为正;λ与λ0分别为目标点经度和覆盖圆起点经度。k为正整数,代表第k天,由于R与D互质,易知当且仅当每经过天数D,目标点在覆盖圆中的投影位置重合。通过式(5)还可将卫星标称轨迹、实际轨迹和覆盖区域投影到覆盖圆中来。
覆盖圆的构造是基于太阳同步回归轨道标称轨迹跳变规律,实际轨迹在大气阻力和轨道维持下有微小漂移。但是由于轨道维持是以标称轨迹为目标,且约束了漂移范围,因此实际轨迹保持相同的回归特性,仍可投影到覆盖圆中进行分析。
3 目标轨迹优化调整方法
太阳同步回归轨道轨道维持通常采用维持实际轨迹和目标轨迹的经度差的方法。在不改变轨道维持方法的情况下,对星座中各个卫星的目标轨迹进行调整即可调整各个卫星的星下点轨迹分布。星下点轨迹的分布直接影响星座的重访性能和星间相位。本节以重访性能和星间相位为优化目标,介绍利用覆盖圆进行目标轨迹优化调整的方法。
3.1 重访性能的分析和优化
考虑不同日的覆盖圆投影图,由于卫星覆盖区域由星下点轨迹决定,在每一天的覆盖圆中,覆盖区域保持稳定不变;由于隔天的轨迹分布网会向东跳变,因此目标点投影到覆盖圆上的位置每天会发生跳变,如图3所示。
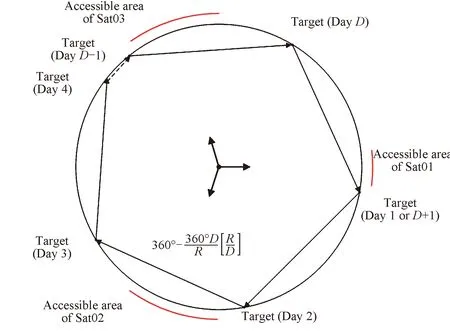
图3 覆盖圆上的覆盖区域和目标点位置Fig.3 Satellite-accessible area and the target on the revisit-circle
可见,在覆盖圆中,目标点和可见覆盖区域的相对位置是随日期变化的,当目标点落于覆盖区域中,则表示当天该目标点被该星可见。
通过覆盖圆投影将每天跳变的卫星覆盖区域相对固定下来,而令目标点在覆盖圆中根据回归规律跳变,有利于根据回归规律优化星下点轨迹的分布。
3.2 星间相位差的分析和调整

综上,构建覆盖圆的方法,可为同时分析和优化星座重访能力和相位间隔提供一个共同的框架。
4 应用实例
本节以某型号测绘卫星为例说明基于覆盖圆的目标轨迹优化调整方法。该型卫星回归周期58 d,回归圈数883圈,由3颗卫星组成,其中01星可侧视1个条带,02、03星可左右侧视2个条带。
4.1 重访性能优化
利用覆盖圆进行分析,首先观察目标在覆盖圆中变化规律,图4为覆盖圆上目标跳变规律示意。
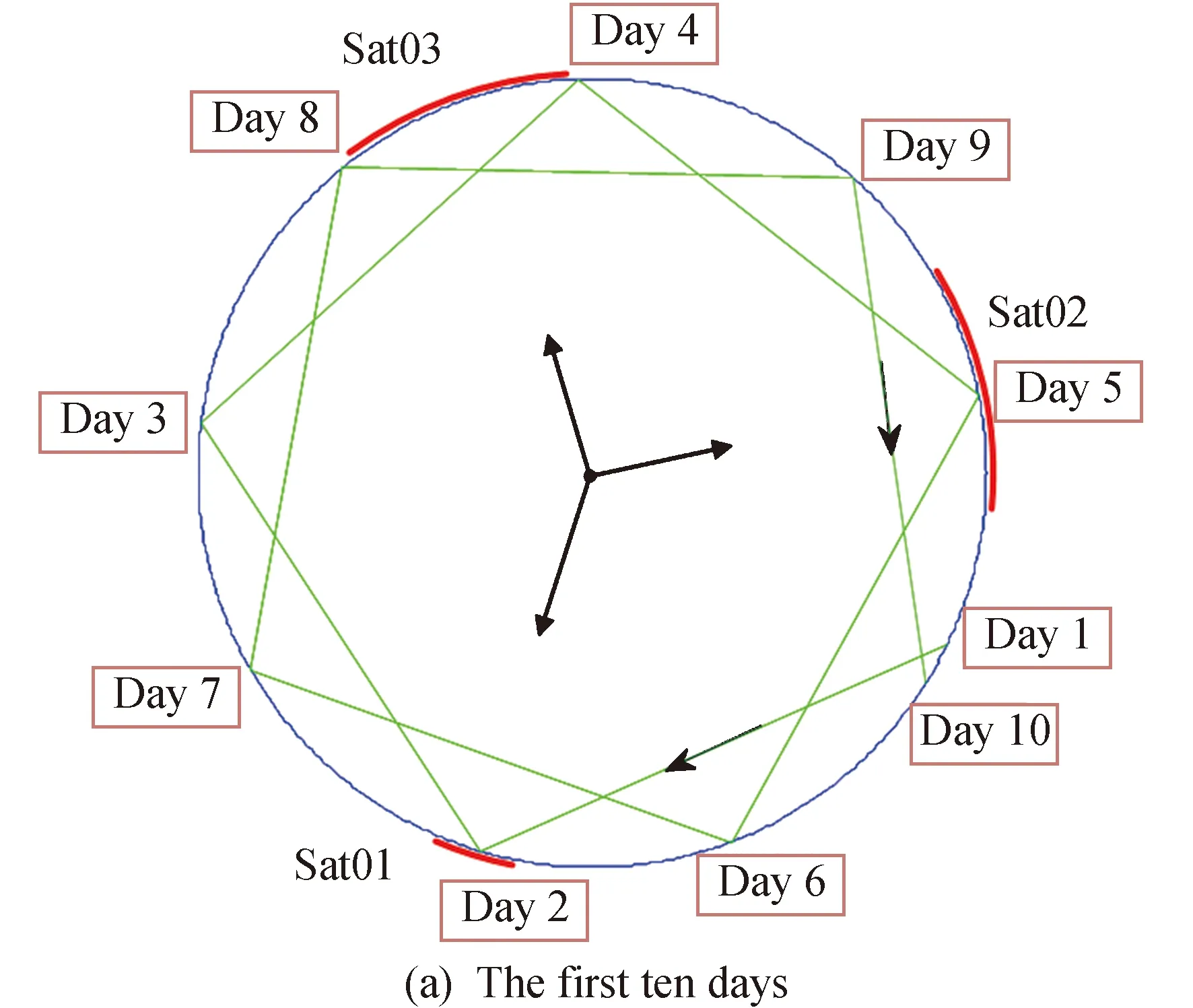
图4 覆盖圆中目标跳变规律示意Fig.4 Pattern of target location changing on the revisit-circle
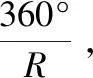
根据目标点在覆盖圆中的位置跳变规律,可以得出覆盖区域分布的以下结论。
1)为了避免短时间内对目标的多次覆盖,使覆盖时间分布均匀,3颗卫星覆盖区域大致应相隔0个或2个星角,不可间隔1个或3个星角。
2)由于九角星形向顺时针方向作微小转动,卫星覆盖区域与星角的位置会逐渐发生变化。对于单星而言,若覆盖区域宽度比星角间的间隙小,则可能陷入星角间隙而导致该9 d内无覆盖,而造成重访间隔变长达13 d;若覆盖区域宽度更小,则可能导致该覆盖区域连续两个9 d陷入星间间隙,造成重访间隔可长达22 d。因此,单星覆盖区的位置选择应尽量避免陷入星角间隙。而对于多星覆盖问题,各星覆盖区应能起到互补作用避免同时陷入星角间隙。
以北纬25°为例,该纬度上各卫星覆盖区域的宽度小于星角间隙。为了使覆盖达到最优效果,覆盖区域分布选择如图5(a)所示布局。该布局中,尽量将01、02、03星的覆盖区域连成片,从而使其起到互补作用,避免出现同时陷入星角间隙而增大重访间隔。或者选择图5(b)所示布局,该布局中在01星覆盖区域因其他原因无法选择图5(a)位置时,选择与该位置间隔一个星角的位置,从而也可对02和03星起到补充作用。

图5 卫星覆盖区域优化布局Fig.5 Optimized layout of satellite coverage area
4.2 星间相位调整
选择该型卫星2016年某时间段作为研究算例,该时间段内各星轨道倾角和轨道维持的目标轨迹未作调整,由于降交点地方时漂移速度不同,降交点地方时之差发生了较大的变化,导致了相位差发生了较大变化。如图6所示,01与03星的相位差后期已达50°,为避免出现接收站冲突需作调整。

图6 三星相位变化Fig.6 Phase change of three satellites
根据式(4)(5),欲使01星和03星的相位差增加60°以上,则在覆盖圆上03星覆盖区域相对01星覆盖区域需向顺时针方向转动60°以上。
在BIM模型上对施工计划和施工方案进行分析模拟,消除冲突,得到最优施工计划和方案。如塔吊定位及运行,工具式模板选型及设计等均可充分利用BIM的参数化和可视化特性对节点进行施工流程的分析模拟,可以改进施工方案实现可施工性。
综合考虑重访性能,可得出覆盖区域分布调整的方案,如图7所示。

图7 卫星覆盖区域调整示意Fig.7 Satellite coverage area adjustment diagram
最终得到相应的目标轨迹调整方案为:01星向东调整4个条带;02星向东调整5.5个条带;03星向西调整5.5个条带。
5 仿真分析
采用上述方案进行仿真,分析相位保持效果,重访性能优化结果以及燃料消耗情况,仿真条件如表1所示,其中Cd为大气阻力系数,Cr为太阳光压系数。
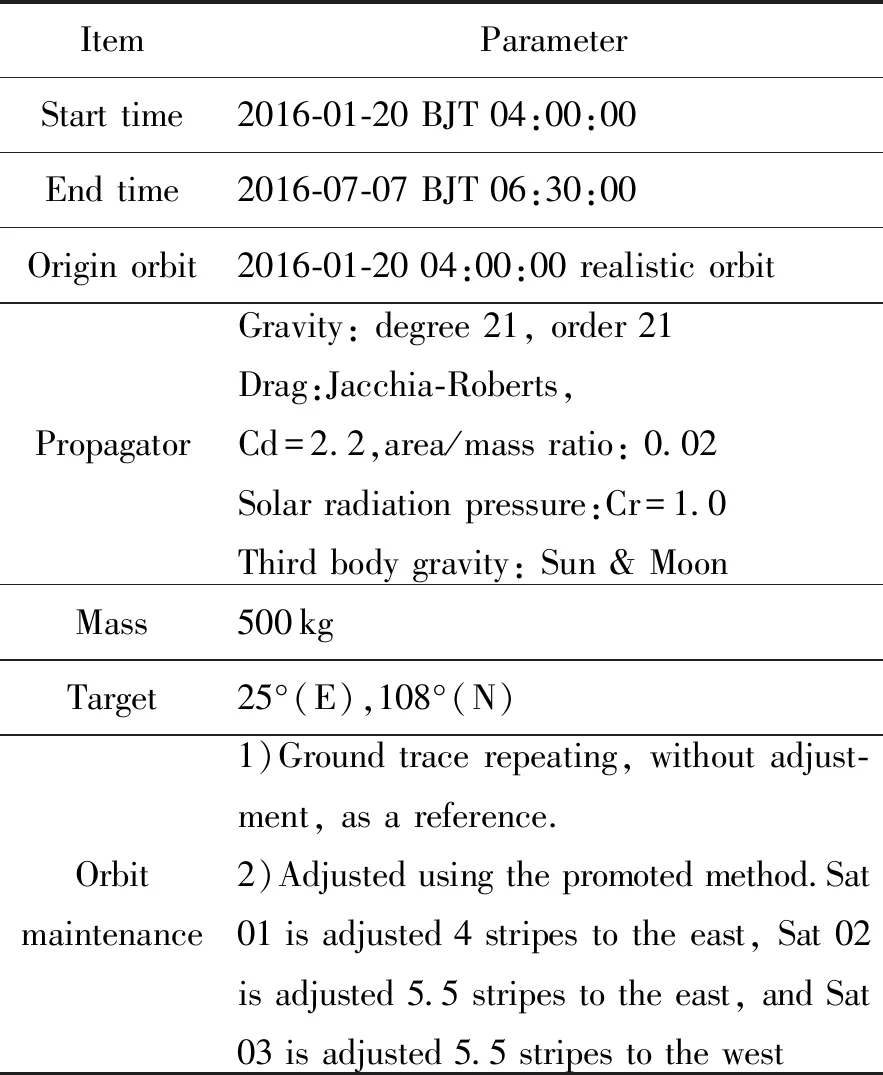
表1 仿真条件Table 1 The simulation conditions
仿真中设置了两组试验,第一组无目标轨迹调整,用于模拟实际运行中的卫星轨道状态,作为第二组的参照,比较采用了本文所述方法的目标轨迹调整后各方面性能的变化。
仿真结果如下所示。
轨迹漂移情况如图8所示。由于目标轨迹调整,01星向东漂移了4个条带后进行轨道维持;02星向东漂移了5.5个条带后进行了轨道维持;03星向西漂移了5.5个条带后进行轨道维持。目标轨迹调整后,轨迹漂移范围一致。

图8 轨道维持下各星轨迹漂移情况Fig.8 The drift of each satellite trajectory under orbit maintenance
(2)重访性能
三颗卫星整体对目标的重访间隔如图9所示。目标轨迹进行调整前,第二组与第一组的覆盖重访间隔无差别;第二组对目标轨迹开始进行调整期间,其对目标重访间隔未出现明显变化;当第二组对目标轨迹调整完成后,其对目标重访间隔稳定在了5 d以下,比第一组最大重访间隔减小了4 d。

图9 三颗卫星整体对目标的重访间隔变化Fig.9 Variation of the revisit time
(3)星间相位
第一组无目标轨迹调整的情况下,星间相位变化如图10(a)所示,01星与03星的相位差逐渐接近并突破50°,极可能出现接收站冲突,与实际运行情况(图7)相同;第二组进行目标轨迹调整后,星间相位变化如图10(b)所示,01星与03星的相位差余量得到了有效增加,使得仿真时段内各星相位差保持在60°以上。

图10 轨道维持下星间相位变化情况Fig.10 Phase changes among satellites under orbital maintenance
(4)半长轴变化情况
仿真时段内卫星半长轴变化如图11所示。
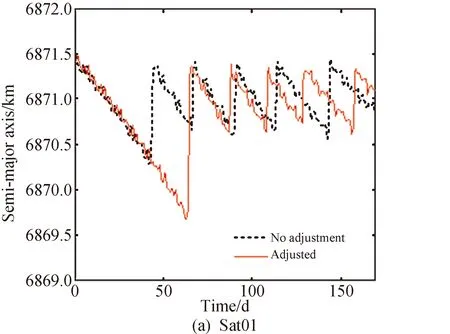
图11 卫星半长轴变化情况Fig.11 Variation of the satellite's semi major axis
从轨道调整过程中半长轴变化情况分析可知,进行目标轨迹调整和不进行调整的轨道高度总调整量很接近,相应的总燃料消耗也差别不大,因而进行目标轨迹调整对整体燃料消耗的影响很小。
6 结论
本文面向遥感卫星运控中重访性能优化和相位保持的应用需求,提出了一种目标轨迹调整方法。该方法有以下主要优点:
1)基于基本交点距提出了“覆盖圆”的概念,将卫星轨道的回归规律转化为目标点在覆盖圆中的跳变规律,将星下点轨迹分布转化为覆盖圆中覆盖区域的分布,从而有利于直观地分析目标点重访规律和对星下点轨迹分布的优化。
2)该方法将星间相位调整问题转化为覆盖圆中覆盖区域相对位置调整问题,从而可实现与重访性能优化问题同时考虑,为解决以上两个问题构建了一个统一的框架。通过应用于某型卫星星座的仿真分析,验证了该方法的有效性。
