基于视惯融合的大型空间碎片质心位置辨识

姚金铭，李广平，张慧博,*，田浩，游斌弟，戴士杰

1. 河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300401 2. 天津市微低重力环境模拟技术重点实验室，天津 300301 3. 哈尔滨工业大学 航天学院，哈尔滨 150001 4. 哈尔滨工业大学(威海) 船舶与海洋工程学院，威海 264209

1 引言

随着人类空间活动的发展，空间碎片的数量日益增多，与在轨航天器的碰撞概率逐渐增大[1-4]。其中，失效卫星和火箭末级等大型空间碎片在碰撞、解体后会产生碎片云，严重威胁在轨航天器安全，因此急需开展大型空间碎片移除任务[5-8]。大型空间碎片尺寸大都超过2 m，受地球引力、太阳光压和残余角动量的影响[9]，往往呈现出40 r/min的三轴翻滚运动[10]。若直接对空间碎片进行消旋、捕获等接触操作，会引起服务星失稳甚至失效，因此需要在接触碎片前获取其动力学参数。在碎片的动力学参数中，质心位置是最为重要的，它是建立服务星与目标星间坐标转换关系、实现后续消旋和捕获操作的关键。

双目视觉是识别空间碎片质心位置的主流方法[5]。文献[11-12]针对空间接近操作的第一阶段[13]，利用双目视觉获取空间碎片特征点坐标，采用增量式平滑和建图方法解决空间非合作目标的参数估计问题，并通过空间站试验[14]证明该方法识别的质心位置三轴误差小于5 mm。但是该方法将识别的特征点几何中心视为目标质心，不符合实际。文献[15-16]提出利用双目视觉识别空间非合作目标的特征点位置和运动速度，进而利用刚体运动理论解算出空间碎片质心位置，并通过数值仿真证明该方法在不同旋转矢量夹角下解算的质心位置三轴方差均小于0.061。但是该方法由于未考虑空间碎片章动，导致解算精度未能符合消旋捕获要求。所以现有双目视觉方法仍无法满足空间碎片清除任务的需求。

文献[17]提出基于惯性单元(IMU)的质心位置辨识方法，该方法利用微型卫星将惯性单元附着到空间碎片上，并基于惯性单元采样频率高、采样精度高、不受空间杂光影响的特性，快速获取碎片运动数据，并实时解算出空间碎片的归一化惯性参数。但是该方法未能识别质心位置，没有建立服务星与目标星间的坐标转换关系，因此无法直接用于针对空间碎片的在轨服务任务。本文深入研究文献[17]的方法，提出基于惯性单元与双目视觉的空间碎片质心识别方法，将多个表面携带发光标记点的惯性单元通过太空鱼叉附着到大型空间碎片表面[18]，通过开展惯性单元冗余测量数据优化，同时辅以双目视觉对标记点的定位数据，实现对碎片质心位置的解算。

本方法基于无力矩欧拉方程建立空间碎片动力学模型，采用并矢坐标变换获取惯性单元坐标系间的转换关系。利用该转换关系开展惯性单元冗余测量数据优化，再利用优化后的数据优化求解惯性单元到质心的距离。基于三角测量原理，获取各时刻发光标记点的三维坐标。利用求得的标记点坐标与惯性单元到质心距离，基于三点定位原理求解各时刻带噪声的质心位置，形成质心点集。最后基于最小二乘原理解算质心坐标，实现对空间碎片质心位置的精确辨识，为后续消旋、捕获操作提供准确、可靠的数据基准。

2 基于视惯融合的质心位置辨识原理

2.1 坐标系系统

本文参考文献[19]，将空间碎片质心识别任务简化为：针对在轨操作第3阶段的追踪卫星对目标碎片T的同轨检测任务，则目标碎片质心在追踪卫星坐标系下可视为常值。其中空间碎片T的中心主轴坐标系M位于碎片质心OT，其各轴均平行于与主惯量矩方向，且z轴指向空间碎片惯量最大方向，所以该坐标系与刚体的质量分布有关，为空间碎片的连体坐标系。

文中考虑了惯性单元k的体坐标系Sk(k=1，2，3)，Sk各轴由传感器出场设置决定，且在发射后未知其空间指向。但是由于惯性单元与空间碎片固连，所以Sk为碎片的连体坐标系。Lk为发光标记点坐标系，其原点位于发光标记点，各轴平行于Sk。在发射前已知其与Sk的方向余弦矩阵及Sk与Lk原点间的向量，该坐标系同样是空间碎片的连体坐标系。

本文将追踪卫星上视觉坐标系C定义在双目视觉的右相机光心OC，其z轴指向空间碎片，x轴与太阳翼平行，y轴与其他两轴垂直且符合右手定则。同时定义其像素坐标系Op-ur-vr，其原点Op位于成像平面左上角，u和v分别表示横纵像素坐标，下标r代表其为右相机的像素坐标。(cu,r,cv,r)为右相机光学中心的像素坐标。各坐标系的示意图如1所示。

2.2 冗余惯性测量数据优化

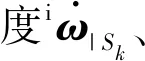
首先需要建立惯性单元间的转换关系。空间碎片位于微重力环境中，可以将其视为无力矩状态下绕质心的刚体定点运动，即欧拉-潘索运动[20-21]。本文利用无力矩欧拉方程进行空间碎片动力学建模，

Jω+ω×(J·ω)=03×1

(1)

惯性张量的基本形式中包含6个独立参数，包括相对三轴的惯量矩及坐标平面的惯量积，表示该坐标系下物体的质量分布。当坐标系中各轴指向惯量主轴时，即在M坐标系下，惯性张量矩阵则变为只包含3个主惯量矩的对角阵(也可归一化为参数Ja和Jb)，此变换可由并矢坐标变换法求得：

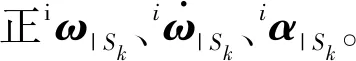
建立数据矩阵：

其中l=1，2，3。利用R|SltoM与R|MtoSk建立目标函数：

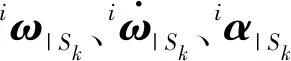
(2)

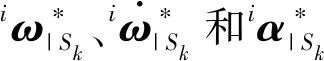
利用刚体定点运动公式，导出第k个惯性单元到质心距离向量rk的计算公式：

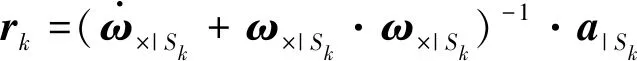
(3)

2.3 质心位置辨识

为进行质心定位，本小节基于视觉三角测量进行标记点定位，再辅以第2.2小节求得的标记点到质心距离，基于三点定位原理求得各时刻的带噪声质心，形成质心点集，最后基于最小二乘原理求解质心位置。本节将基于对极约束，辅以不同颜色的发光标记点进行左右相机图像匹配。坐标系及原理示意如图2所示。

图2 质心识别原理Fig.2 Reference frames and coordinate systems

i时刻视觉坐标系C上第k个惯性单元上发光标记点位置可以通过三角测量法求得，

式中：fr为右相机的焦距；b为基底；(iur,k,ivr,k)为i时刻右相机测得的第k个惯性单元上发光标记点的像素坐标。双目相机在测量前已经进行了相应的标定和图像校正，保证了两个相机的焦距和光学中心像素坐标相等，即fr=fl=f，cu,r=cu,l，cv,r=cu,l。相机相关的坐标系如图1所示。

图1 坐标系系统Fig.1 Reference frames and coordinate systems

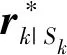
利用i时刻视觉测量的标记点的位置和rk|Lk，在每个采样时刻建立3个球面，可知在视觉数据准确的情况下，质心应该位于3个球面的交点处。但由于视觉存在测量误差，球面大概率不能在一点相交，所以质心应定位在空间中与球面距离最短的点上，进而转化为一个无约束优化问题。所以可以建立目标函数：

iRk=(iOx|C-iXk|C)2+(iOy|C-iYk|C)2+

(iOz|C-iZk|C)2

其中，

iOT|C=[iOx|CiOy|CiOz|C]T

进行多个时刻的质心求解可以得到质心点集，利用最小二乘法，求得空间中到点集中坐标点的距离最小的一点，则该点为较为准确的质心位置：

ΔO=(iOTx|C-Ox|C)2+(iOTy|C-Oy|C)2+

(iOTz|C-Oz|C)2

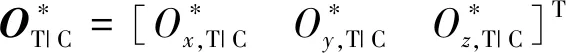
图3 算法流程Fig.3 Algorithm flow chart

3 质心位置辨识仿真

为了证明L-M算法对本文问题的有效性和可靠性，本节运用蒙特卡洛分析法对比L-M算法和扩展卡尔曼滤波算法对惯性单元1坐标系下J|S1的计算效果。为简化计算，设置空间碎片为2 m×2 m×2 m的大型空间碎片，采用张贴质量块的方式改变其主惯量矩(归一化主惯量矩分别为2.6、2、1)，碎片质心位于视觉坐标系下的(-1 m,1 m,4 m)处；设定仿真次数为100次，每次的仿真初始值设置为从(0 m,0 m,0 m)到(-0.9 m,0.9 m,2.9 m)的随机点；在该仿真中有3个惯性单元附着到了空间碎片上，各惯性单元连体基与碎片主轴间的夹角已知，且其与质心的距离分别为1.5 m、1.6 m、1.6 m，惯性单元上设置发光标记点，以提高较差光照条件下的视觉定位精度；参考文献[9]，将所有噪声设置为零均值高斯分布，考虑极端的光照环境，将视觉数据设为标准差为2.2像素的高斯分布，其数值大于文献[16]的1像素，视觉采样频率设为20 Hz；参考传感器实际的出厂设置，将惯性单元的采样频率设置为200 Hz，同时考虑实际测量值和空间环境影响，将其出厂标定的标准差放大3倍，其中角速度误差分布的方差为0.008 7 rad/s，角加速度误差分布的方差为0.017 44 rad /s2，线加速度的误差方差为0.980 1 m/s2，碎片的初始角速度设置为[1 10 2]r/min；设置每采样5个点进行迭代计算，最大迭代次数设置为10。对J|S1的仿真如表1所示。

表1 L-M算法与扩展卡尔曼滤波算法对比Table 1 Comparison of L-M algorithm and extended Kalman filter algorithm

由表1可知，在100次不同初始条件的仿真中， L-M算法实现了全部收敛，而扩展卡尔曼滤波只有87次收敛。经分析是由于有13次的迭代初始值与真实值相差较远，使得观测方程误差较大，导致扩展卡尔曼滤波不收敛，而L-M算法受初始条件影响较小，因此实现了全收敛。在收敛的仿真中，两种算法的最终误差均能收敛到0.025左右，但L-M算法由于更好的局部收敛性，所以比扩展卡尔曼滤波更快收敛。因此针对文中无约束优化问题，选用稳定性更好、收敛速度更快的L-M算法。针对碎片质心位置辨识的仿真结果如图4～7及表2所示。

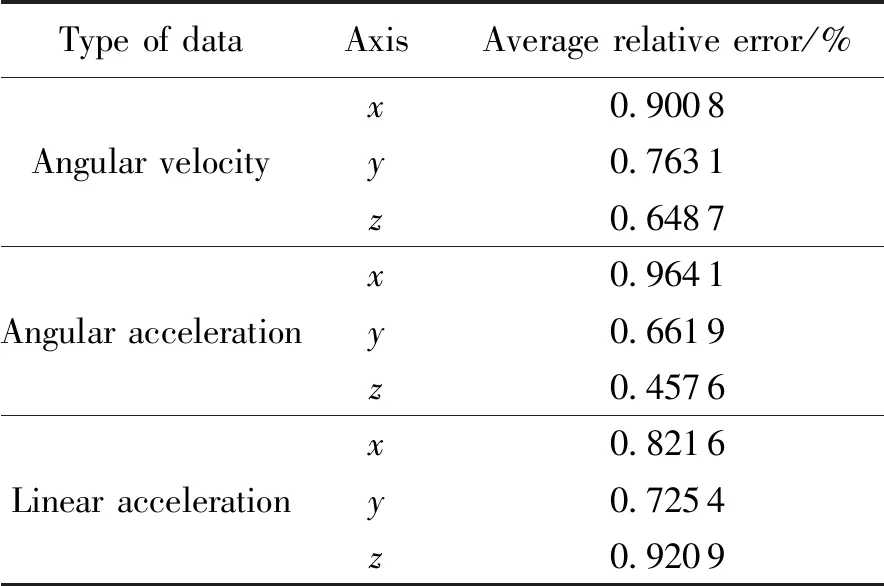
表2 仿真结果：惯性单元冗余测量数据优化后误差Table 2 Results of simulations: error of redundant inertial measurement unit’s data after optimization

针对惯量矩测量，6参数惯性张量与3参数主惯量矩矩阵的转换是通过并矢坐标变换求得，同时惯性张量与惯性矩的误差与惯性单元坐标系间方向余弦误差是正相关的。因此为了使图像表达更为清晰，本节采用三参数主惯量矩矩阵衡量惯性张量和方向余弦矩阵的辨识效果，并采用文献[11-12]对观测性的归一化方法，将3参数主惯量矩矩阵进一步简化为两个归一化主惯量矩(分别为Ja和Jb)。如图4所示，可以看到当计算到2.09 s后，归一化主惯量矩误差收敛到0.03(无量纲)以下，该辨识精度符合后续计算要求，证明本文模型计算效果较好；同时由于本算法需要的数据量较小，计算时间较短，所以能够降低随机干扰的影响。

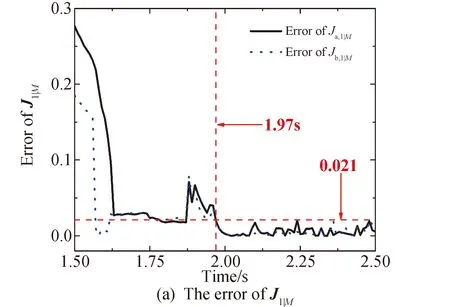
图4 仿真结果：归一化主惯量矩误差Fig.4 Results of simulations: error of normalized principal moment of inertia

惯性单元冗余测量数据的实时优化结果如表2所示，可以看到，角速度的三轴平均相对误差均小于或等于0.900 8%，角加速度的三轴平均相对误差均小于或等于0.964 1%，而线加速度的三轴平均相对误差均小于或等于0.920 9%。惯性单元测量数据优化后的相对误差均降低到1%以下，实现了较好的实时优化效果，为后续的质心解算提供了良好的数据支持。

图5显示了惯性单元到质心距离的仿真误差，可以看到在计算到2.55 s后，3个惯性单元到质心的距离均收敛到0.98 mm以下，符合质心求解的精度及实时性要求。

图5 仿真结果：惯性单元到空间碎片质心的距离误差Fig.5 Results of simulations: the error of the distance from the inertia sensors to the mass center of the space debris

图6显示了质心识别的过程。3种不同颜色小点代表不同传感器上标记点的视觉定位坐标，而较大的红色圆点表示质心点集，左上角的放大图为质心点集的优化过程；图7为质心识别的误差曲线，可以看到当计算时间达到6.83 s时，质心的三轴误差均收敛到0.47 mm以下，解算的数据精度符合消旋、捕获的任务要求。

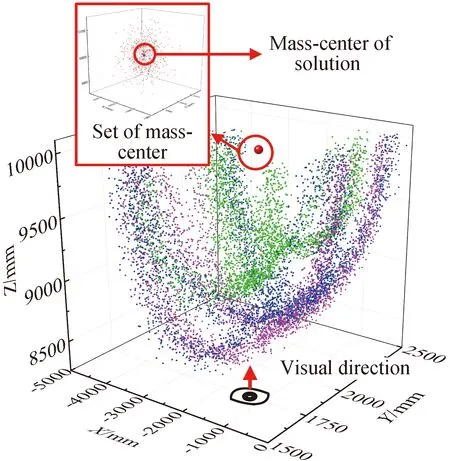
图6 仿真结果：质心识别结果三维图Fig.6 Results of simulations: three-dimensional diagram of the mass-center recognition result

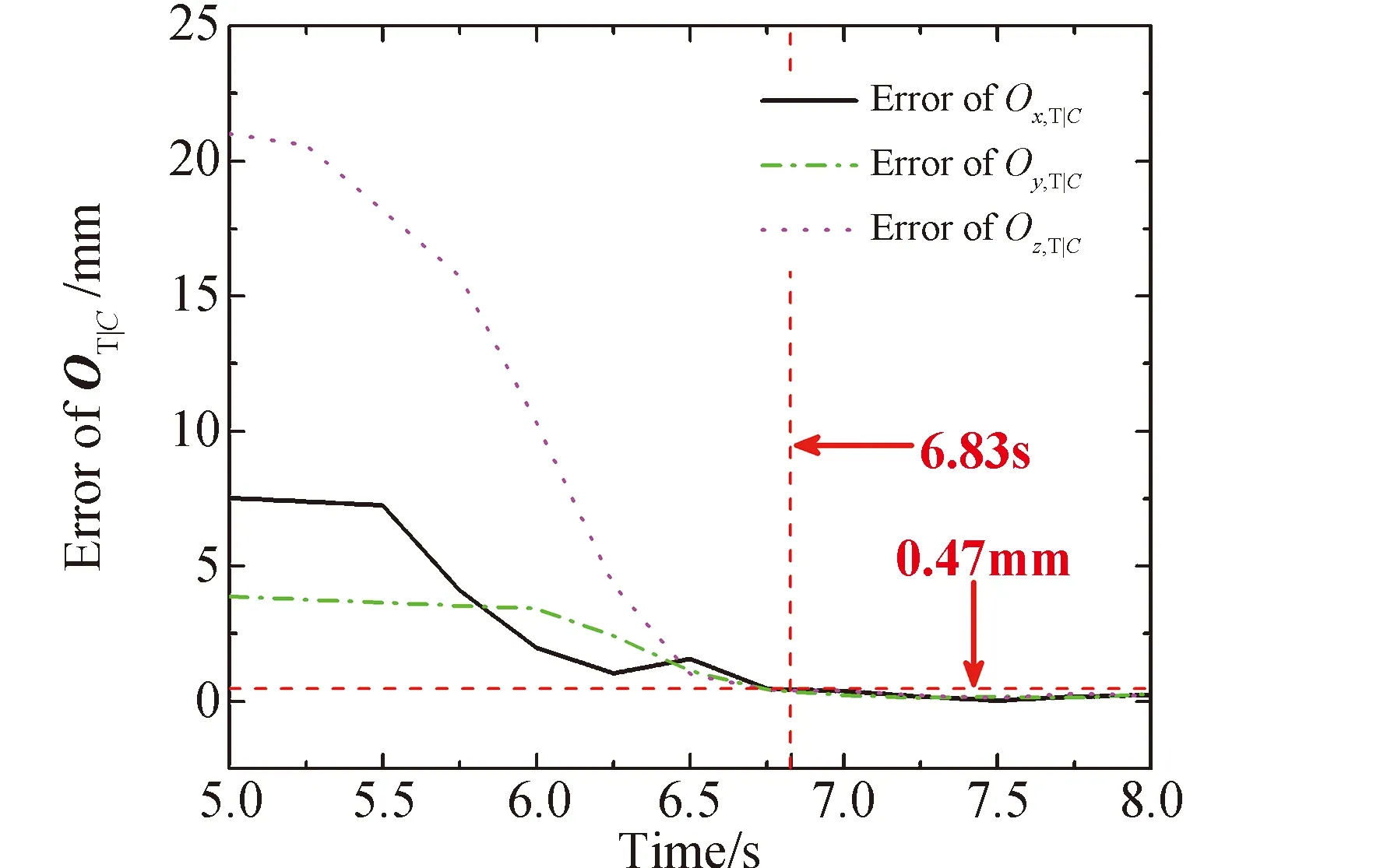
图7 仿真结果：质心位置识别误差Fig.7 Results of simulations: error of mass-center location identification

4 质心位置辨识地面试验

为了验证本方法的有效性和可靠性，本节开展了地面模拟试验。设计的地面模拟试验系统如图8所示，其中所用的3个惯性单元为WT-901，其采样频率为200 Hz，通过Wifi与上位机通信，各惯性单元与质心的距离分别为0.3 m、0.32 m、0.32 m，惯性单元参数如表3所示；惯性单元表面粘贴了不同颜色的标记点，以模拟太空环境中的发光标记点；所用双目相机为MYNTAI-S2110，其采样频率为20 Hz，分辨率为720×480，双目参数如表4所示；碎片模拟装置为等比例缩小的仿真模型，尺寸为0.4 m×0.4 m×0.4 m，质心位于视觉坐标系(-0.2 m,0.2 m,0.8 m)处；选用球铰作为回转构件，以实现碎片的三轴旋转；参考现有航天器质量特性调整机构，设计了一套十字滑台与质量块的组合装置作为调心机构，质量块为对称设置的铝合金块和不锈钢块，以实现数值为2.6、2和1的归一化主惯量矩；设置试验装置的初始角速度与仿真对应，均为[1，10，2]r/min，试验数据如图9所示。

图8 试验装置Fig.8 Experimental device

表3 惯性单元性能指标Table 3 Performance index of IMU

表4 双目相机性能指标Table 4 Performance index of binocular camera

图9 试验数据Fig.9 Experimental data

由于试验中惯性单元冗余测量数据的优化效果较难恒定，但其辨识结果与惯性单元到空间碎片质心距离的计算结果正相关，因此只进行归一化主惯量矩、惯性单元到空间碎片质心的距离误差及碎片质心位置的求解，试验结果如图10～12所示。

图10 试验结果：归一化主惯量矩误差Fig.10 Results of experiments: normalized principal inertia moment's error of experiments

可以看到，当计算到5.42 s时，3个惯性单元的归一化主惯量矩(无量纲)均收敛到0.027以下；当计算到6.79 s时，惯性单元到质心向量的三轴误差均下降到0.86 mm以下，以该误差衡量惯性单元冗余测量数据优化结果，可知优化后惯性单元测量数据平均相对误差小于1.1%，证明了该方法可以实现较好的优化效果；在9.21 s时，解算的质心位置三轴误差收敛到0.49 mm以下。相比于仿真，试验中算法的收敛时间变长，其主要是受球较处摩擦力、空气阻力以及调心误差等系统误差的影响，导致参数优化需要更多的数据点，从而使收敛时间增加。

表5为本方法的仿真、试验结果与文献[19]的双目视觉方法仿真结果、文献[11]的双目视觉方法试验结果的对比。可以看到，由于双目视觉受空间复杂光照条件的影响，其测量精度低于惯性单元，因此本方法的收敛时间和误差小于纯视觉方法；Tweddle的双目视觉方法识别对象为惯性对称物体，因此其将碎片特征点的几何中心辨识为碎片质心，但是其在用于非惯性对称对象时存在一定的质心偏移，而本方法采用碎片的动力学特性识别空间碎片质心，所以本文方法更符合实际，同时本文方法的质心识别误差小于文献[11]的双目视觉方法。上述对比证明本方法更符合工程实际需求。

图11 试验结果：惯性单元到空间碎片质心的距离误差Fig.11 Results of experiments: the error of the distance from the inertia sensors to the mass center of the space debris

图12 试验结果：质心位置识别误差Fig.12 Results of experiments: error of mass-center location identification

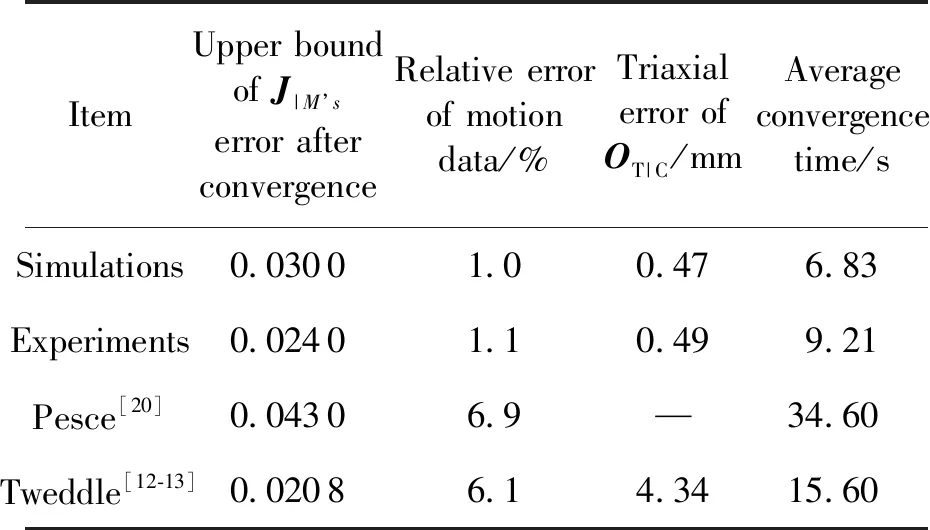
表5 本文算法与现有双目视觉方法对比Table 5 Comparison of the algorithm with existing binocular vision methods

5 结论

本方法针对火箭末级、失效卫星等大型空间碎片的质心位置辨识问题，提出了基于惯性单元和双目视觉数据的空间碎片质心位置识别方法，基于惯性单元的实时性和双目视觉的定位优势，提高质心辨识精度。基于无力矩欧拉方程，通过并矢坐标变换求得主轴坐标系对应的归一化主惯量矩，同时获取惯性单元间的方向余弦矩阵，建立惯性单元间的转换关系，以加入高斯白噪声的惯性单元与视觉测量数据进行数值仿真，仿真表明当计算到2.09 s时3个惯性单元的归一化主惯量矩误差(无量纲)均收敛到0.03以下。搭建了地面模拟试验系统，试验表明在计算到5.42 s时，3个惯性单元的归一化主惯量矩误差(无量纲)均收敛到0.024以下；基于惯性单元间转换关系，进行惯性单元冗余测量数据的实时优化，优化后的角速度、角加速度、线加速度瞬时三轴误差均小于1%；利用优化后的惯性单元测量数据，解算出惯性单元到质心点的向量，仿真结果表明在计算到2.55 s后的该向量的三轴误差收敛到0.98 mm以下，试验中在5.89 s后该向量的三轴误差小于0.86 mm，以试验中该三轴误差衡量优化结果，可知优化后惯性单元测量数据平均相对误差小于1.1%；基于三点定位原理，求解各时刻带噪声的质心位置，形成质心点集，再基于最小二乘原理进行了质心位置的优化求解，当仿真时间大于6.83 s、质心位置三轴误差小于0.47 m、试验时间大于9.21 s时，质心位置三轴误差均小于0.49 m。仿真和试验数据证明该方法精度高，实时性好，满足空间碎片清除任务的需求，能够大幅提高消旋、捕获动力学参数的检测精度，为针对空间碎片的在轨服务任务提供准确的数据基础。