激光复混沌系统构建及其点乘函数投影同步
2021-12-26姜明浩安小宇
方 洁,姜明浩,安小宇,邓 玮
(1.郑州轻工业大学电气信息工程学院,郑州 450002;2.河南省信息化电器重点实验室,郑州 450002)
0 引言
混沌是非线性动力系统的固有特性,是非线性系统普遍存在的现象。牛顿确定性理论能够充分处理的多为线性系统,而线性系统大多是由非线性系统简化来的。因此,在现实生活和实际工程技术问题中,混沌是无处不在的。目前,混沌理论已经在数学、生物学、信息技术、经济学、工程学、物理学、等众多科学学科中得到广泛应用[1-5]。
在现代通信技术特别是全光网络高速发展的趋势下,光学混沌及其保密通信技术以其独特的优势受到了国内外的广泛关注。半导体激光器是光纤通信中最常用的光源之一,通过引入附加自由度可以产生丰富的非线性动力学行为,如果选择合适的控制参数,可输出高维混沌光信号[6-9]。混沌光信号具有不可长期预测性和类噪声特性,特别适用于混沌保密通信中。随着各种激光混沌系统的提出与验证,混沌光通信己经成为一种能够克服数值计算加密安全性低的实用通信技术[10-12]。
相对于实混沌系统,复混沌系统将混沌系统的状态变量从实数域扩展到复数域上,增加了系统状态变量的数目,使得混沌系统具有更加复杂的动力学行为。复混沌系统深厚的物理背景及更加不可预测和随机的状态变量的特性使得其在保密通信领域有着巨大的应用潜力,吸引了很多学者对复混沌动力学系统进行研究,并取得了一系列进展。文献[13]研究了一个三维混沌复系统的基本性质,实现了系统的自适应混沌同步和参数识别。文献[14]针对含未知参数的异结构超混沌复系统,基于自适应控制及Lyapunov稳定性理论,提出一种新的自适应广义组合复同步方法。文献[15]研究了时滞复Lorenz系统的动态特性及时滞因数的影响,并基于非线性反馈控制方法实现了复Lorenz系统的自时滞混沌同步。文献[16]基于自适应控制方法研究了具有已知或未知参数的复混沌系统的修正函数投影同步。文献[17]基于滑模控制方法研究了具有未知参数和外界干扰的分数阶复混沌系统的完全同步。文献[18]基于非线性控制策略研究了具有参数扰动的分数阶复混沌系统的双重相同步和反相同步。文献[19]以超混沌复系统为载体,研究了该系统的动力学行为,通过将脉冲注入控制参数中来增强该混沌系统的随机性,并将其应用于彩色图像加密中。文献[20]构建了一个新的复混沌系统,分析了其动力学行为,实现了3个复混沌系统的组合函数投影同步。已有复混沌系统及其同步研究大都是基于复混沌电路,目前还鲜有关于激光复混沌系统的有关报道。
本文在上述研究的基础上,基于四维激光实混沌系统模型,构建出一个新的具有蝴蝶型混沌吸引子的激光复混沌系统,基于非线性动力学理论对其耗散性、平衡点、Lyapunov指数谱、相图、分叉图等动力学特性进行了分析,验证了系统的混沌行为。然后,在向量点积运算的基础上,提出了一种点乘函数投影同步方式,基于Lyapunov稳定性定理,设计具有积分环节的滑模面和自适应滑模控制器,实现了蝴蝶型激光复混沌系统的点乘函数投影同步。研究成果为激光复混沌系统应用于光保密通信等领域奠定了基础。
1 多翼蝴蝶型激光复混沌系统模型
四维激光实超混沌系统的模型为[4]:
(1)
式中f0,f1,f2,Ω为实常数。当f1=0.01,f1=0.01,f2=0.01,0.45<Ω<0.98或Ω>0.22时,系统有两个正的Lyapunov函数,为超混沌状态。
(2)
当f0=1,f1=0.01,f2=0.01,Ω=0.6时,该系统相图具有蝴蝶型混沌吸引子,如图1所示。采用雅阁比方法计算系统的Lyapunov指数,得到LE1=0.119 665,LE2=0.074 812,LE3=0,LE4=-0.100 009,LE5=-0.059 122,LE6=-0.162 011,LE7=-0.147 536,其Lyapunov指数仿真结果如图2所示。混沌系统的一个典型特征就是其Lyapunov维数为分数维。计算该系统的Lyapunov维数为DL=3.456 266 35,进一步说明在此参数下系统是混沌的。
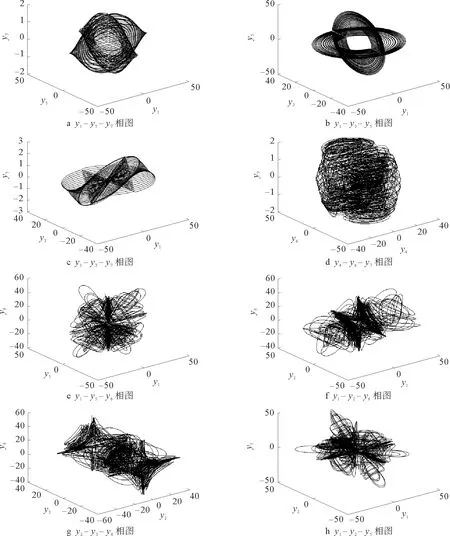
图1 混沌吸引子相图
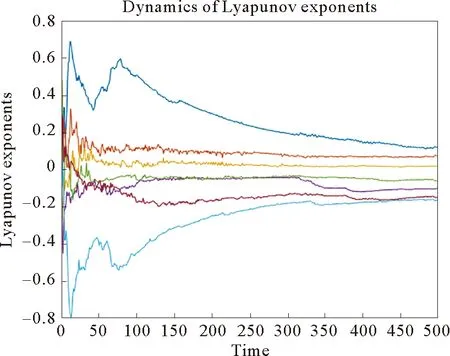
图2 Lyapunov指数谱
2 激光复混沌系统动力学特性
2.1 耗散性分析
该激光复混沌系统的向量场散度
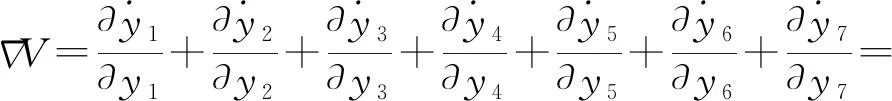
(3)
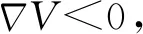
2.2 平衡点及稳定性分析
记:
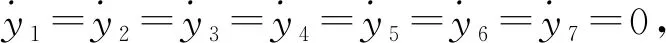
E0=[2Af2(A-f1)/B,0.5B/f1,A,-f1,0,-D,0]
E1=[2Af2(A-f1)/B,0.5B/f1,A,-f1,0,D,0]
为了分析系统在平衡点E0处的稳定性,对系统(2)进行线性化得其Jacobian矩阵:
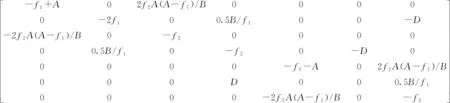
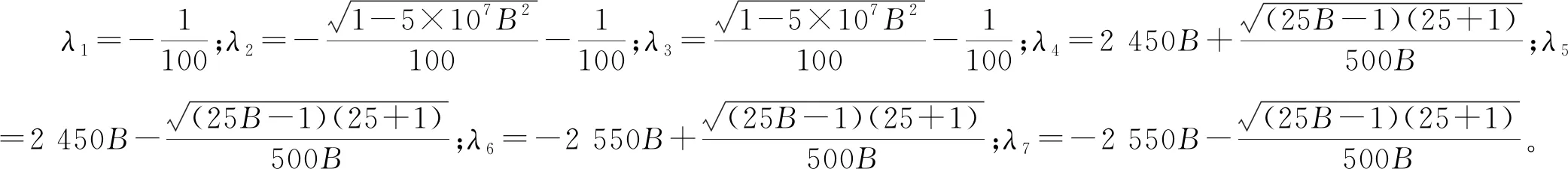
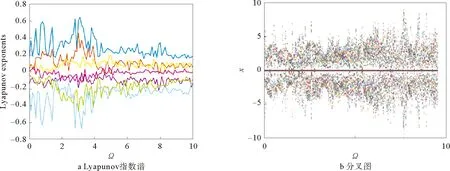
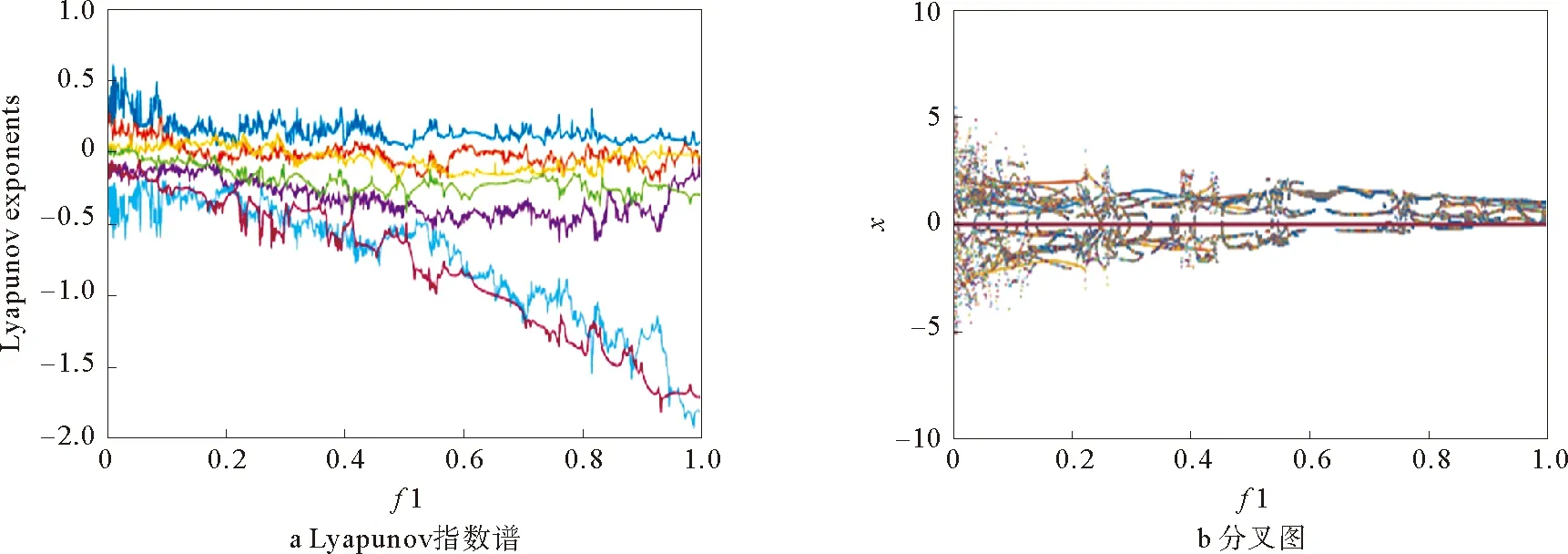
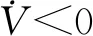
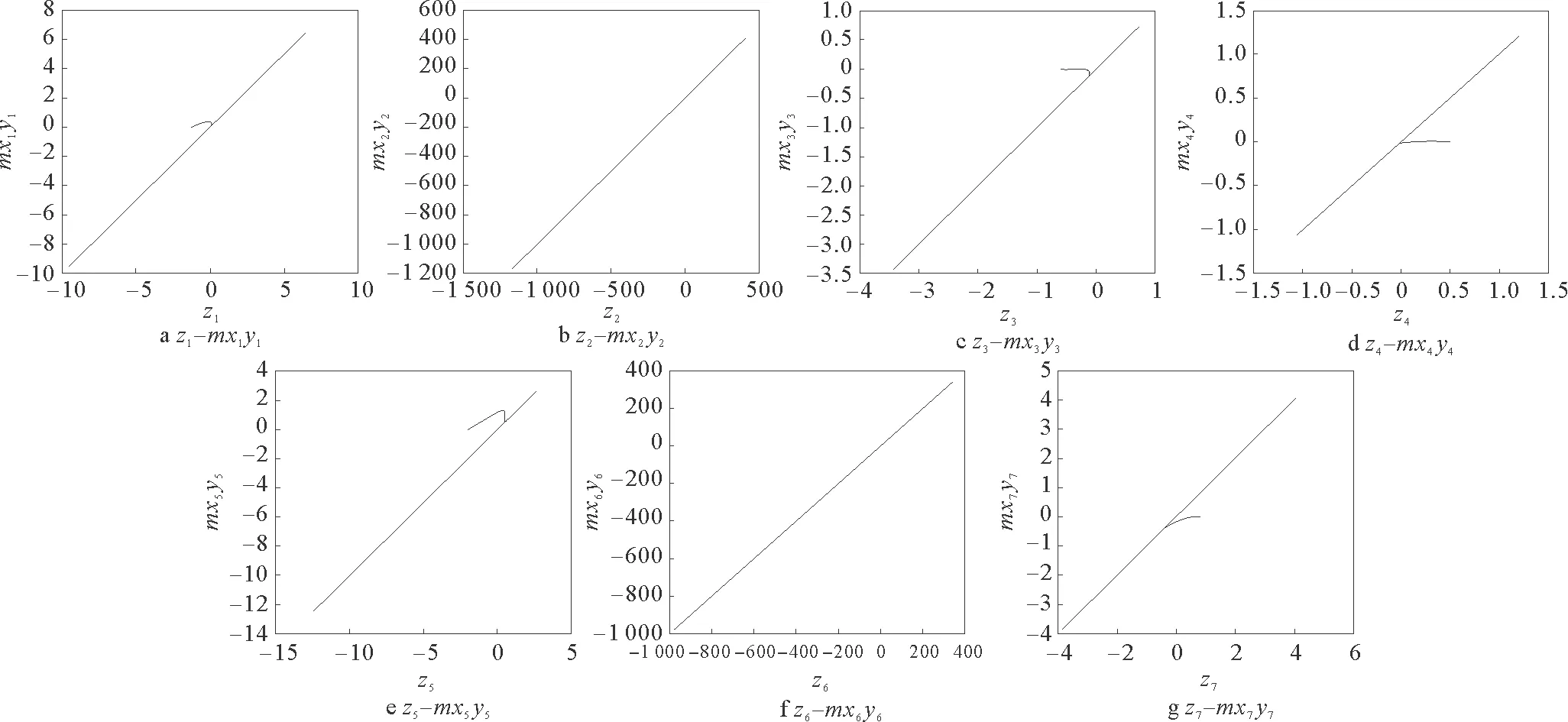
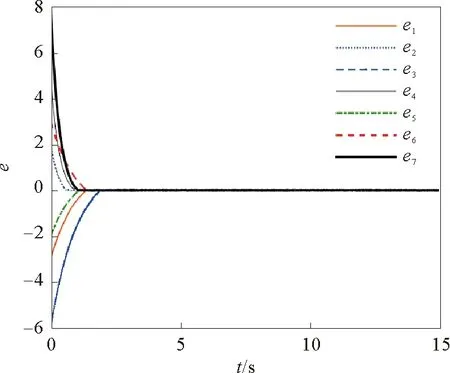
显然有λ1<0。当0 在平衡点E1处的Jacobian矩阵为: 选取参数f0=1,f1=0.01,f2=0.01,计算出J1的特征值和J0完全相同,因此随着B在0≤B=1+sin(Ωt)≤2范围内取值变化,平衡点E1也是不稳定的焦点或不稳定的鞍点。 随着参数的改变,系统平衡点的稳定性将会发生变化,从而使系统处于不同的状态。用Lyapunov指数谱及分岔图可以对照分析系统参数改变对系统动力学行为的影响。下面分别分析参数Ω和f1在一定范围内改变时,系统动力学行为的变化。 1)固定参数f0=1,f1=0.01,f2=0.01,改变Ω,Ω∈(0,10)。激光复混沌系统的Lyapunov指数谱及分岔图如图3所示。由图3可知,当Ω∈(0,0.3)时,系统的Lyapunov指数有4个正值,3个负值,系统是超混沌的;当Ω∈(0.3,4.4)时,系统的Lyapunov指数有3个正值,4个负值,系统超混沌的;Ω∈(4.4,10)时,系统的Lyapunov指数有3个正值,1个零值,3个负值,是超混沌的。 图3 Ω∈(0,10),随参数Ω变化的系统图 2)固定参数f0=1,f2=0.01,Ω=0.6,改变f1,f1∈(0.003,1)。激光复混沌系统的Lyapunov指数谱及分岔图如图4所示。由图4可知,当f1∈(0.003,0.17)时,系统的Lyapunov指数有2个正值,1个零值,4个负值,系统是超混沌的;当f1∈(0.17,0.3)时,系统的Lyapunov指数有2个正值,5个负值,系统是超混沌的;当f1∈(0.3,1)时,系统的Lyapunov指数有1个正值,6个负值,系统是混沌的。 图4 f1∈(0.003,1),随参数f1变化的系统图 同步系统由两个混沌驱动系统和一个混沌响应系统组成,第一个混沌驱动系统定义为 (4) 另一个混沌驱动系统定义为 (5) 混沌响应系统定义为 (6) (7) 则称驱动—响应系统实现了点乘函数投影同步。 设计滑模面如式(8): (8) 其中,si(t)∈R为滑模面函数;滑模面参数λi(t)>0,i=1,2,…,n为合适的正常量。 设计如式(9)的滑模到达律: (9) 由式(7)可得同步系统的动态误差为 (10) 为了确保误差系统轨迹到达已设定的滑模面,并保持在滑模面上,可设计如式(11)的滑模同步控制器。 (11) 定理1对于同步误差动态系统(10),在滑模同步控制器(11)的作用下,可以使得同步误差轨迹快速进入设定的滑模面内,并始终保持在滑模面上。 证明:选择正定的Lyapunov泛函为 (12) 对其求导可得: (13) 根据式(8)和式(10)可得: (14) 将式(11)代入式(14)可得: (15) 为了验证上述方案的正确性,将激光复混沌系统(2)分别作为驱动系统和响应系统进行仿真实验。第一个驱动系统的初始值取为(x1(0),x2(0),x3(0),x4(0),x5(0),x6(0),x7(0))=(-3,2,-0.6,0.5,-2,3,0.8);第二个驱动系统的初始值取为(y1(0),y2(0),y3(0),y4(0),y5(0),y6(0),y7(0))=(-0.3,2,0.6,5,-0.9,3,1);响应系统的初始值取为(z1(0),z2(0),z3(0),z4(0),z5(0),z6(0),z7(0))=(0.3,2,1.5,1,-0.8,1,2);函数比例因子为m(t)=2+sin(t);取λi=ρi=5,i=1,2,…,n。驱动系统与响应系统的同步状态曲线如图5所示,同步误差e1,e2,e3,e4,e5,e6,e7随时间t的变化曲线如图6所示。由仿真结果可知,在控制器的作用下,驱动系统与响应系统的状态曲线趋于一致,同步误差e逐渐趋近于零,即驱动系统和响应系统通过滑模控制实现了点乘函数投影同步。 图5 驱动系统与响应系统的同步状态曲线 图6 同步误差随时间t的变化曲线 本文在激光实混沌系统的基础上构建了一个蝴蝶结型激光复混沌系统,利用耗散性、平衡点、Lyapunov指数谱、相图及分叉图等对其基本动力学特性进行了分析。随着参数变化,该系统呈现复杂的混沌、超混沌现象,非常适用于混沌加密领域。进一步,以向量点积运算为基础,定义了一种新的点乘函数投影同步方式,基于滑模控制思想,实现了两个驱动系统和一个响应系统的点乘函数投影同步。以新构造的激光复混沌系统为例的仿真实验验证了理论方法的有效性。研究成果为激光复混沌系统的光保密通信应用提供了理论基础。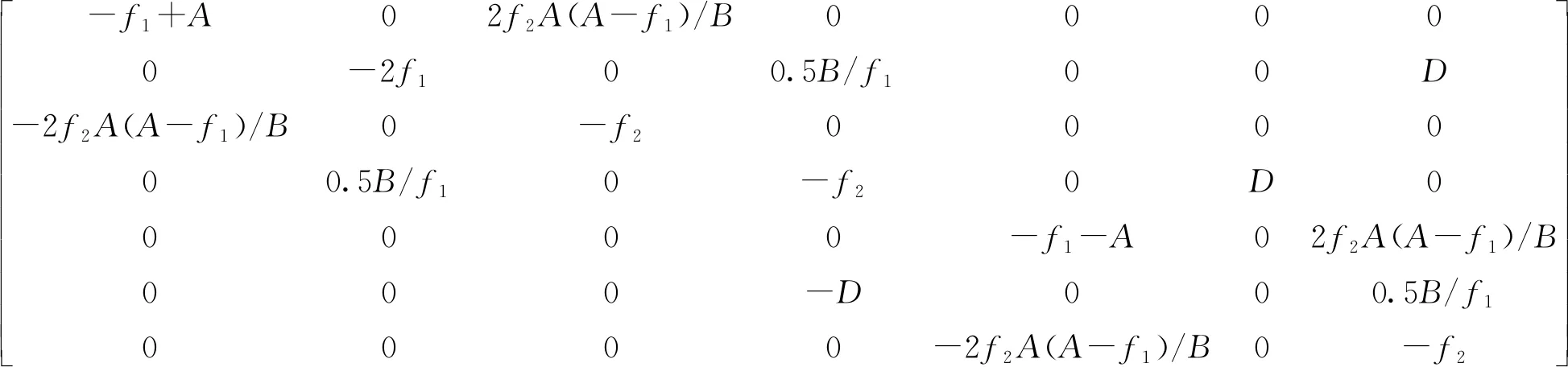
2.3 Lyapunov指数谱及分岔图
3 激光复混沌系统的点乘函数投影同步
3.1 问题描述
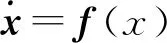
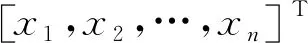
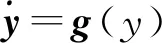
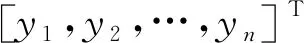
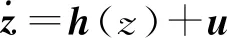
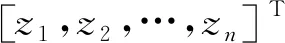
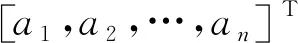
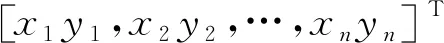
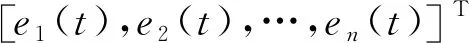
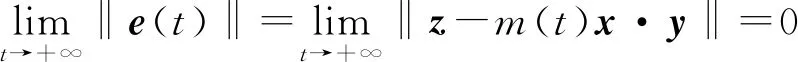
3.2 滑模控制器设计
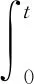
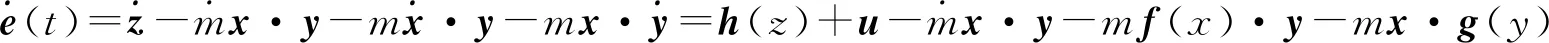
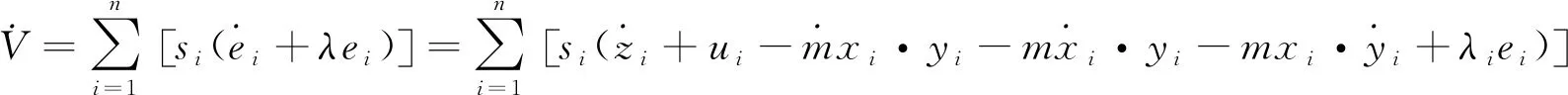
3.3 数值仿真
4 结论
