具有数据包丢失的网络控制系统的估计问题

韩 笑，亓庆源，纪志坚

(青岛大学自动化学院，山东 青岛 266071)

0 引言

网络控制系统(NCSs)是空间分布式系统，其中传感器、控制器和执行器通过共享的网络实现通信[1-2]。因为NCSs具有成本低、重量轻、结构简单和提高系统可靠性的优点，所以被广泛应用于远程手术，无人机，人工智能等领域[3-5]。然而，在网络控制系统信息传递过程中，网络通信带宽有限、网络拥塞和网络连接中断等现象都会导致系统产生数据包丢失的问题[6]。由于丢包的存在，系统的状态信息不能精确得到，只能依赖接收到的量测信息来对系统进行分析，使得系统的估计状态有效的跟踪实际状态，具有重要的实际意义[7]。对于具有数据包丢失的NCSs，经典的卡尔曼滤波失去了有效性，不能直接用来设计估计器[8-9]。因此，估计器可以通过量测过程zk推导出来。

近几十年来，对具有数据包丢失的网络控制系统进行研究已经成为一个热门的话题。Nahi考虑了具有数据包丢失的网络控制系统的估计器，并得到了线性最小均方差估计器(LMMSE)[10]。然而，在文献[11]中LMMSE是次优的。文献[12]利用时间戳技术，在随机过程γk的条件下推导出了间歇卡尔曼滤波器。Imer提出了具有不可靠通信信道的线性时不变系统的最优控制[13]。对于UDP网络的最优控制，虽然控制具有双重效应，但它们给出了一个最优估计器。然而，估计器是否是最优的并没有得到证明。Qi考虑了具有数据包丢失的网络控制系统的最优测量反馈控制和镇定性[14]。Zhang等提出了一种次优估计量[15]，它可以看作是LMMSE与间歇卡尔曼估计器的折中。

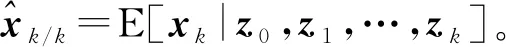
本文在之前工作的基础上扩展了有关的内容，给出了UDP情况下的最优估计器，得到的结果可以在将来解决相关的最优输出反馈控制问题。本文通过严格的计算，运用递推的方法得到两种不同情形下系统的最优估计(基于条件期望)和协方差矩阵。但是，在大的有限域下，这种方法变得困难。所以为了简单的使用，本文开发了一个次优估计器，这对研究在大的有限域下含有丢包的网络控制系统有所帮助。

主要符号说明：Rn表示n维Euclidean空间；AT意味着矩阵A的转置；E[·]是数学期望；E[·|Zk]是对Zk的条件期望；δkl表示Kronecker Delta函数，当k=l时，δkl=1；否则δkl=0；P(A)是事件A发生的概率，P(A|B)描述条件概率；I{A}是指示函数，表示当元素ω∈A时，I{A}=1,否则I{A}=0；N(μ,Σ)表示具有均值为μ，协方差为Σ的正态分布。

1 经典卡尔曼滤波

卡尔曼滤波(Kalman filtering)是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

1.1 系统模型

考虑以下经典的动态系统：

(1)

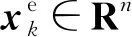
假设1在整个论文中，做出如下假设：

1)假设ek和vk是独立的，均值为0的高斯白过程。

(2)

2)进一步假设初始状态x0是一个具有均值为μ和协方差为E[(x0-μ)(x0-μ)T]=P0的高斯随机变量，它与{ek}和{vk}相互独立。

确定估计器和相关的误差协方差矩阵：

(3)

(4)

(5)

1.2 主要结果

引理1[23]考虑经典的动态系统：

(6)

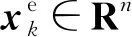
(7)

(8)

(9)

(10)

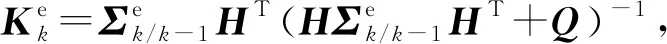
2 具有丢包的网络控制系统

网络控制系统的通信通道通常使用以下两种协议之一：传输控制协议(TCP)或用户数据报协议(UDP)。两者的区别之一是数据在网络控制系统中传输时，是否发生丢包的行为是可知还是未知的。若是可知的，称之为TCP情形下的网络控制系统，反之，则称之为UDP情形下的网络控制系统。

为了基于量测过程{z0,z1,…,zk}来估计系统状态xk，在给出最优估计器之前，首先介绍如下的引理。

引理2[24]假设X,Y为任意联合分布的随机变量，则当随机变量Y取值为y时，对随机变量X的最小均方差估计可以如式(11)计算:

(11)

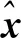
2.1 系统丢包过程γk可知

假设γk在每一个k时刻都能够直接观测到，随机过程γk与量测数据zk在估计器设计中都是可知的。考虑动态系统：

(12)

其中，xk∈Rn是状态过程，zk∈Rn是量测信息，A∈Rn×n，H∈Rn×n是给定的确定性矩阵，γk∈{0,1}描述了数据从执行器传输到控制器的丢包过程。

假设2γk是独立同分布(i.i.d)的Bernoulli随机变量，其中P(γk=1)=p,P(γk=0)=q=1-p。

确定估计器和相关的误差协方差矩阵：

(13)

(14)

(15)

其中，Zk表示集合{z0,z1,…,zk}。

定理1在假设1与假设2的条件下，对于给定的动态系统(12)，最优估计可计算为：

(16)

(17)

Σk/k=I{zk=0}Σk/k-1+I{zk≠0}[Σk/k-1-KkHΣk/k-1]

(18)

Σk+1/k=AΣk/kAT+R

(19)

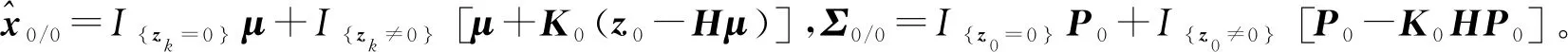
最优估计器与文献[12]中所得的结果一致。

其中,γk是独立同分布的伯努利随机变量，概率为P(γk=1)=p。

证明：

(20)

fx0|z0(x|z)是条件概率密度函数。

(21)

其中,fx0,z0是(x0,z0)的联合密度函数，fz0(z)是z0的概率密度函数。

1)当z0=0时，x0,z0相互独立，f(x0,z0)=f(x0)f(z0)。

(22)

(23)

2)当z0≠0时，

x0/0=E[x0|z0=Hx0+υ0]

(24)

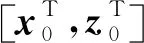
(25)

因此，在这种情况下，x0是条件为z0的高斯随机向量，可以得到以下式子

(26)

Σ0/0=P0-P0HT(HP0HT+Q)-1HP0

(27)

定义K0=P0HT(HP0HT+Q)-1，因此，

(28)

(29)

由于系统噪声{ek}和{γk}是相互独立的，由公式(12)可得

(30)

(31)

由于z1是以z0为条件的，所以

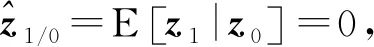
(32)

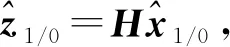
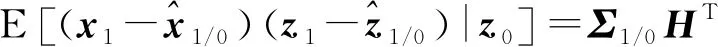
(33)

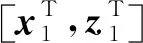
应用于基本的结果，可以得到在z0和z1条件下x1的均值为

(34)

协方差为

Σ1/1=Σ1/0-Σ1/0HT(HΣ1/0HT+Q)-1HΣ1/0

(35)

因此，

(36)

(37)

(38)

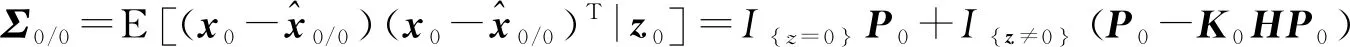
(39)

(40)

Σk/k=I{zk=0}Σk/k-1+I{zk≠0}[Σk/k-1-KkHΣk/k-1]

(41)

(42)

证毕。

2.2 系统丢包过程γk未知

本节中考虑随机过程γk不能直接被观测到的情形，其中仅知道γk的概率分布。

系统的动态方程为

(43)

其中，xk∈Rn是状态过程，zk∈Rn是量测信息，A∈Rn×n，H∈Rn×n是给定的确定性矩阵。

假设3{γk}是独立同分布(i.i.d)的Bernoulli随机变量，其中，P(γk=1)=p,P(γk=0)=q=1-p。另外，γk不能在系统中观测到。

定理2在假设1和假设3的情况下，系统(43)的最优滤波可以通过迭代的方法推得

(44)

(45)

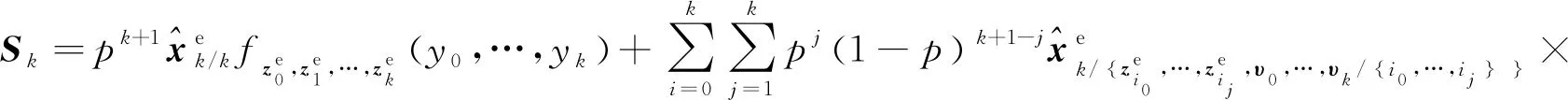
(46)

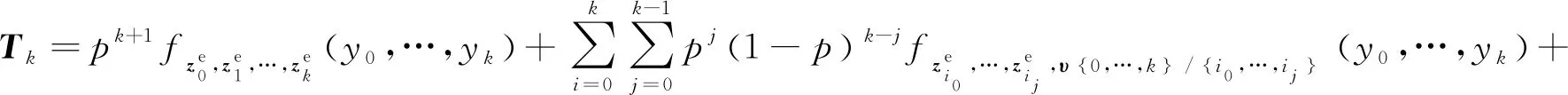
(47)

(48)

Σk+1/k=AΣk/kAT+R

(49)

证明：

(50)

其中,fx0|z0(x|z)是条件概率密度函数，

(51)

fx0,z0是(x0,z0)的联合密度函数，fz0(z)是z0的概率密度函数。

1)当γ0=0时，

fz0(y)=fυ0(y)，fx0,z0(x,y)=fx0(x)fυ0(y)

2)当γ0≠0时，

其中，

(52)

(53)

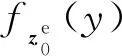
Fx0,Hx0+υ0(x,y)=P(x0≤x,Hx0+υ0≤y)

Fx0,υ0(x,y)=P(x0≤x,υ0≤y)

(54)

(55)

进而得到，

(56)

(57)

由于x1=Ax0+e0，所以

(58)

(59)

则最优估计

(60)

定义fx1,z0,z1(x,y,z)=Δ1,fz0,z1(y,z)=Δ2，

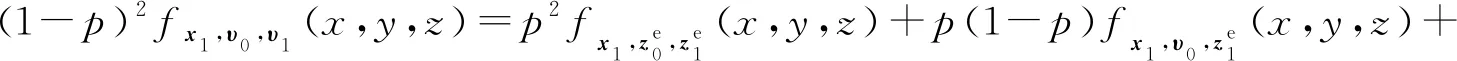
(61)

Δ2=p2fHx0+υ0,Hx1+υ1(y,z)+p(1-p)fυ0,Hx1+υ1(y,z)+p(1-p)fHx0+υ0,υ1(y,z)+(1-p)2fυ0,υ1(y,z)

(62)

(63)

(64)

(65)

以此类推，可以得到：

(66)

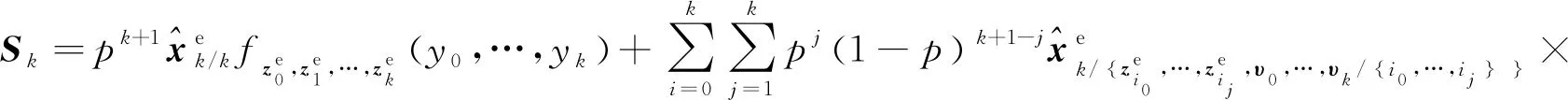
(67)

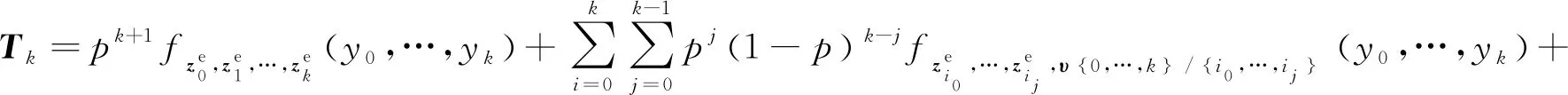
(68)

(69)

Σk+1/k=AΣk/kAT+R

(70)

证毕。

由于求得的最优滤波太复杂，难以实际应用，因此，为了更简单的使用，需要给出一个次优近似估计器。这种情况考虑的基本模型中没有量测噪声，不包括任何量测噪声的理由是假设传感器和控制器之间的通信发生在网络层，其中发送的数据包是接收或丢失的。或者，也可以认为传感器和控制器通过具有无限容量的二进制擦除信道连接，即没有状态的量化或编码。

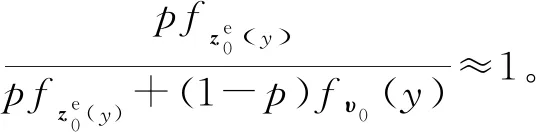
(71)

定理3对于系统(70)，基于量测过程{z0,…,zk}的次优估计器可以表示为

(72)

(73)

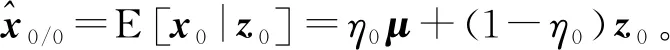
证明：具体证明过程参考文献[14]。

3 数值算例

在本节中，将进行数值仿真模拟来进一步说明理论结果。一方面，通过图1展示在网络控制系统中经典卡尔曼滤波的最优性。另一方面，对于具有数据包丢失的网络控制系统，本文给出定理1最优估计与定理3次优估计的仿真实例，并且分别与线性最小均方差误差估计(LMMSE)进行比较。

3.1 卡尔曼滤波

假设经典动态系统(1)的参数：A=1，H=0.2，ek～N(0,1)，vk～N(0,1)，时域N=200。由图1可以看出，对于经典的动态系统，系统观测值与真实值的误差比较大，而卡尔曼滤波的结果与系统真实值的误差较小，能有效跟踪系统的状态。

3.2 最优估计

由于在具有数据包丢失的NCSs当中，经典的卡尔曼滤波失去有效性，因此，本文通过量测过程推导出系统的最优估计器。首先对于随机过程γk能直接被观测到的情形，针对定理1，假设线性离散随机系统(12)的参数：A=1.01，H=1，ek～N(0,1)，vk～N(0,1)，μ=0，P0=1，p=0.4，时域N=100。

从图2可以明显看出本文得出的最优估计器与系统真实值之间误差较小，而LMMSE与系统的真实状态误差较大，因此验证了本文定理1的有效性。

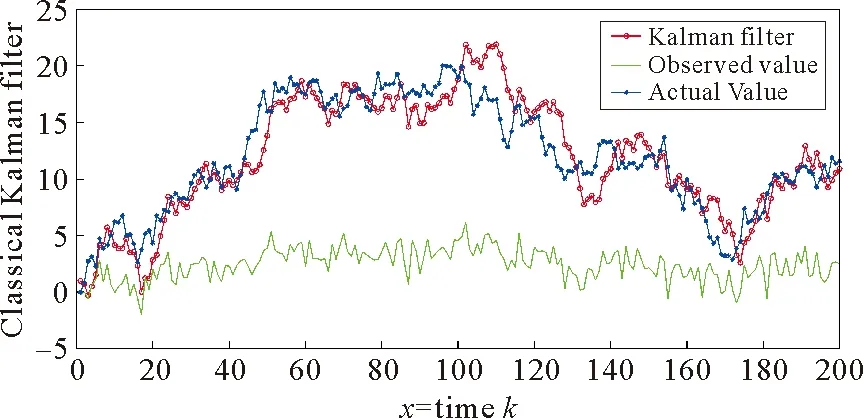
图1 系统的真实状态，观测值与卡尔曼滤波之间的比较

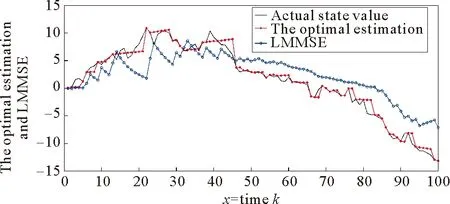
图2 系统的真实状态，最优估计与LMMSE之间的比较

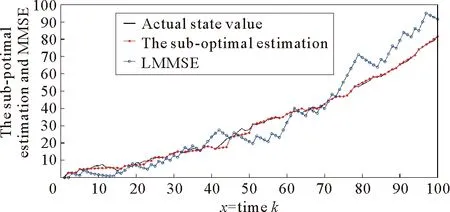
图3 系统的真实状态，次优估计与LMMSE之间的比较

3.3 次优估计

对于随机过程γk不能直接被观测到的情形，由于求得的最优滤波太复杂，不能实际应用，所以本文只考虑次优估计器的数值算例。因此，针对定理3，假设系统(71)的参数为：A=1.02，H=0.8，ek～N(0,1)，μ=0，P0=1，p=0.4，时域N=100。

从图3中可以明显看出本文给出的次优估计器与系统的真实值的误差比较小，而LMMSE与系统的真实值误差比较大，由此证明本文提出的方法是可靠的。

4 结论

本文对具有丢包的网络控制系统的估计问题进行了研究，当量测方程带有噪声时，由于经典的卡尔曼滤波失效，针对不同的情形采用递推的方法求出了系统的最优估计(条件期望)和协方差矩阵。同时，为进一步研究大的有限域下的网络控系统的问题，开发了一个次优估计器，具有实际应用价值。最后，通过数值模拟验证了文中提出的估计器能有效跟踪系统的状态，并且比LMMSE的性能更好，本文提出的方法是可行的。因此，研究具有数据包丢失的网络控制系统的估计问题具有重要的理论和现实意义。