动态围堵嫌犯模型
2021-12-26冯倩倩周伟刚陈仕军
冯倩倩,周伟刚,陈仕军
(湖北文理学院数学与统计学院, 湖北 襄阳 441053)
0 引言
调度分布在城区的交巡警平台的警力围堵嫌犯的问题,称为围堵嫌犯问题[1]。该问题为2011年全国大学生数学建模竞赛的赛题之一,已被广泛地研究[2-13]。已有的研究都假设只知道嫌犯开始逃跑的位置和时间,在围堵嫌犯的过程中,不能实时获取嫌犯的位置信息。然而,借助设置在大街小巷的大量摄像头组成的监控网络“天网监控系”,交巡警指挥中心可以不断更新嫌犯所在位置。充分利用这些实时获取的信息,能更好地围堵嫌犯。在警力不足时,甚至有可能没有实时信息时不能将嫌犯围堵住,有实时信息则可以将嫌犯围堵住。本文拟研究可以实时获取嫌犯的位置信息假设下的围堵嫌犯问题,称之为动态围堵嫌犯问题。
虽然文献[2]早在2012年就指出动态围堵嫌犯问题是值得研究的课题,但是到目前还找不到相关的研究文献。文献[14]利用基于“状态机”思想的协同控制方法,研究了网格图形上多警察协作围堵系统。文献[14]中的网络不是一般的路网,也不是用数学建模的方法。所以该成果也不能算是这里要研究的动态围堵嫌犯问题的成果。
文献[2]~[11]通过不同的方法建立了围堵嫌犯数学模型,并设计了问题的求解算法。文献[12]~[13]建立的模型可以直接用Lingo等运筹学软件求解,这两篇文献的模型是基于文献[12]给出的点截集判断优化模型。我们将修改文献[12]的点截集判断优化模型,以建立动态围堵嫌犯模型。
1 问题分析
1.1 基本假设
在围堵嫌犯的过程中,嫌犯在交叉路口选择新的逃跑方向,在一条边中间遇到前方有交巡警时选择掉头。先假设嫌犯在逃跑路口节点不会选择有交巡警先到而将其堵住的路口节点作为逃跑方向,并假设嫌犯和交巡警都是匀速,且速度相等。因此,可以假设只有在嫌犯到达路口节点时更新嫌犯的位置信息。对速度不相等的情况,只需对模型稍作修改。
1.2 问题的难点
动态围堵嫌犯问题较非动态的围堵嫌犯问题有两个难点:1)在路口节点处嫌犯选择下一步逃跑方向时,交巡警一般都不在路口节点处,而可能在路网的任意位置,调度交巡警问题为连续变量决策问题。2)嫌犯从一个路口节点逃到另一路口节点的这段时间内,因为时间较短,交巡警可能不能形成包围圈,文献[12]给出的点截集方法将交巡警包围住嫌犯作为约束条件加入调度决策模型中,如果在嫌犯从一个路口节点逃到另一路口节点的这段时间内的调度决策模型中加入交巡警包围住嫌犯约束,会导致模型无可行解,所以不能直接利用文献[12]给出的点截集方法。因此,动态围堵嫌犯问题为具有较大难度的问题。
对于前一难点,若用连续优化的方法,需要考虑两个方面,每次重新调度都不是节点到节点的调度;重新调度时,需将交巡警的当前位置作为新的节点,构造新的网络。这种考虑方法留作进一步的研究。本文对网络的边进行分割,将新网络看成等边长网络。新网络下,先假设嫌犯和交巡警的速度相等,嫌犯和交巡警在单位时间内移动一个边长的距离,所以可以采用节点到节点的离散优化方法建模。当边的分割细度变小,点到点的指派可以逼近连续的指派。对于后一难点,考虑带有缺口的包围圈。每次重新调度时,以最小化缺口的大小和交巡警尽量靠近嫌犯为目标。文献[12]的点截集模型是不含缺口的包围圈,建立以缺口点和有交巡警的围堵点一起构成包围圈的模型。
1.3 关于动态的说明
嫌犯在路口节点选择新的逃跑方向时,重新调度交巡警,因此假设当前时刻为嫌犯在路口节点i的时刻,当前状态为嫌犯和所有交巡警在此时的位置和嫌犯选择的下一个路口节点j。当前时刻到下一时刻要经历的时间为嫌犯从路口i逃到路口j所需时间,决策为将所有的交巡警从当前位置调度到新的位置。每一个时刻的重调度问题除了参数不同,问题都相同,因此只需建立一个重调度问题的模型。然后根据实时获取的嫌犯逃跑路径信息重新调度,或者判断在下一时刻前是否能将嫌犯包围住。
接下来,首先考虑重新调度交巡警的模型;然后考虑:设定嫌犯选择下一逃跑目标点的规则,并给出动态围堵嫌犯的模拟流程。在现实的围堵嫌犯问题中,嫌犯的选择由嫌犯自己决定,不属于决策范围。
现实的动态围堵嫌犯问题,除了考虑信息更新下的重新调度,还会考虑研判,即根据经验、网络特点、嫌犯逃跑的特点,预测嫌犯更长距离的逃跑目标。本文将研判问题留作进一步的工作。
2 重新调度模型
无向网络G=(V,E),点集V={1,2,…,n},E为边集。对任意边(i,j),其边长记为dij,将其等分成[dij/L]段(中括号表示取整),分割后的边长大约为L,L的取值可根据实际问题的精度要求确定。L越小,对于求解来说问题的规模越大。G分割边后视为等边长网络,新网络记为G′=(V′,E′)。对任意边(i,j)∈E′,更改其边长为dij=1。单位时间内交巡警和嫌犯移动的距离都为1。交巡警初始位置集合J⊂V′,记交巡警平台总数为|J|。假设一个平台的警力只能负责一个节点的封堵任务,一个节点也只需一个平台的警力就可以堵截嫌犯。嫌犯每到达一个节点并开始朝另一节点逃跑的时刻,需根据新的嫌犯移动信息,重新调度交巡警。用0表示当前状态,1表示指派方案执行后的下一个状态。已知嫌犯当前位置节点s0和逃跑方向为从s0到s1,边(s0,s1)∈E。
假设在边(s0,s1)上没有交巡警,也没有交巡警可以先于嫌犯到达s1。对于边(s0,s1)上有交巡警或交巡警可以先于嫌犯到达s1的情况,只需对模型稍作修改。
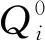
从点i派出去的警力小于等于点i处的警力资源数,即
并有pji和pij中至少有一个为0,即
pjipij=0,i,j∈V′,i≤j
(1)
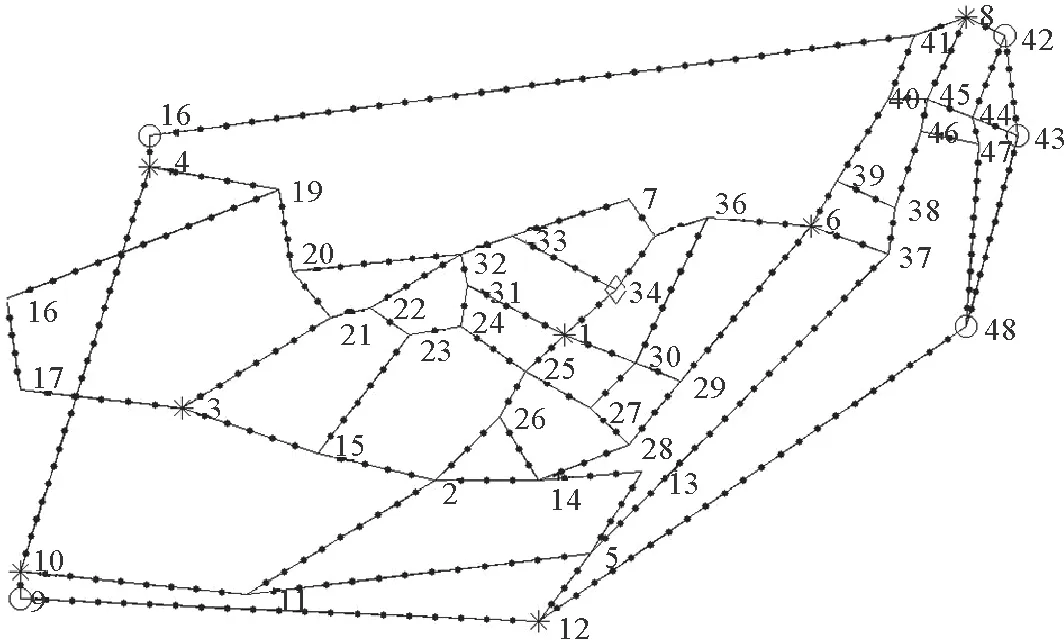
特别地,piipii=0使得pii=0。为了将(1)线性化,定义变量Pij,i Pij≥pij 同时成立与(1)等价,即(1)可线性化。 在嫌犯从s0到s1这段时间,交巡警移动的距离不超过ds0s1,若点i到点j的距离超过ds0s1,不能指派点i处的交巡警到点j,即 (dij-ds0s1)·pij≤0,i,j∈V′ (2) 警力分布Q0、Q1和指派方案p在点i处的平衡关系表示为 (3) 即“节点i当前的警力资源数+派往节点i的警力-派出节点i的警力=节点i下一阶段的警力资源数”。 为了让警力朝嫌犯靠近,以嫌犯到达下一个路口节点时所有的交巡警尽量靠近嫌犯为目标,即 其中,dis1表示点i到嫌犯下一阶段的位置s1的最短路长,dis1为已知量。 若只以交巡警尽量靠近嫌犯为目标,可能会导致有的路口没被封堵,而形成缺口,嫌犯从缺口逃脱。为了考虑包围圈的缺口问题,定义0-1变量γi和ψi,对i∈V′, xs1=1 (1-ψi)(1-ψj)xi=(1-ψi)(1-ψj)xj,(i,j)∈E′ (4) xT=0 xi∈{0,1},i∈V′ 其中,T为连接所有城区出入口的虚拟点。文献[12]给出了约束(4)的线性化方法。以包围圈缺口点尽量少为目标,即 当目标值π2=0时,无缺口,警力形成有效围堵。在之后的模拟中,以此作为模拟结束条件之一。 以π1和π2为目标,得到重新调度交巡警的多目标优化模型1。 模型1 π1(p),π2(p) 因约束集的所有非线性约束均可线性化,模型1可化为线性整数规划模型。在此模型基础上,读者还可以参考文献[12-13],考虑其它目标函数。在后面的模拟计算中,通过加权求和将模型1的多目标化为单目标。 假设边(s0,s1)上无交巡警,即 (5) 假设嫌犯能先于所有交巡警到达节点s1,即 (6) 因为假设交巡警和嫌犯的速度相等,当(6)成立时,(5)一定成立。 当满足(6)的点s1不存在时,假设嫌犯被包围,模拟结束。当由模型1计算得π2=0时,嫌犯被包围,模拟结束。 嫌犯到达当前位置s0前,在图G上经过的点记为s-1∈V。记 假设嫌犯选择下一个点s1遵循规则1。 记城区出入口集合为C。动态围堵嫌犯的模拟流程为流程1。 流程1 1)输入初始值s0,Q0。初始时刻不存在s-1点。 2)由规则1,若嫌犯被包围,模拟结束;否则确定出逃点s1,若s1∈C,嫌犯逃脱,模拟结束;否则转下一步。 4)更新s-1:=s0,s0:=s1,Q0:=Q1,返回1)。 对文献[13]的算例作如下修改,将边长为dij的边(i,j)等分成[dij/L]段,取L=2,得到图1所示网络,平均边长为1.961 7分钟的路程(60km/h),其边长集合的方差为0.033 8,计算中将分割边得到的网络当作等边长网络。图1中,标有数字的点为图G的点,所有的点都是图G′的点。菱形标记的节点为嫌犯的出逃点,星号标记的节点为交巡警平台分布节点,圆圈标记的节点为城区出入口。 图1 算例网路 文献[13]的计算表明该算例不考虑实时获取嫌犯位置信息时可以围堵住嫌犯。但是如果撤掉交巡警平台6,利用文献[13]的模型和程序,通过计算发现不能将嫌犯围堵住。 将交巡警平台6撤掉,由模拟流程1模拟动态围堵嫌犯,用MATLAB、YALMIP、Gurobi求解模型1。对于两个目标,分3种情况进行模拟: 1)不考虑目标1,出现了嫌犯成功逃脱的情形,也出现了嫌犯逃跑经过了40条边才被围堵住的情形。 2)不考虑目标2,也出现了嫌犯成功逃脱的情形。 3)多目标化为π1+π2,进行多次模拟,都能较快地将嫌犯围堵住。 若不同的交巡警速度相等,但嫌犯的速度与交巡警的速度不相等。记交巡警的速度为v,嫌犯的速度为vs,交巡警的指派仍采用网络G′上点到点的指派,此时的模型只需将模型1的约束(2)修改为 若不同的交巡警的速度也不相等,问题变得更为复杂,需要区分不同的交巡警,记住交巡警所处的位置,在模型1的基础上不难建立模型。 监控网络被广泛应用、影像识别和智能科技不断发展的时代,动态围堵嫌犯问题的研究具有较大的应用价值。本文的研究只是通过数学建模对动态围堵嫌犯问题的初步探索,可以进一步研究根据经验、网络特点、嫌犯逃跑的特点预测嫌犯的逃跑目标,并用于动态围堵决策中。
Pij≥pji
Pij=pij+pji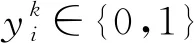
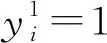
3 模拟
3.1 流程
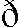
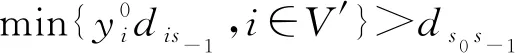
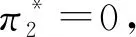
3.2 算例
4 速度不相等时的模型
5 小结
