具有logistic增长的SIS传染病模型动力学分析

聂勇冰，侯 强

(中北大学 理学院，山西 太原 030051)

0 引 言

文献[1]利用函数h(I)=cI/(b+I)反映疾病治疗的情况，提出以下传染病模型：

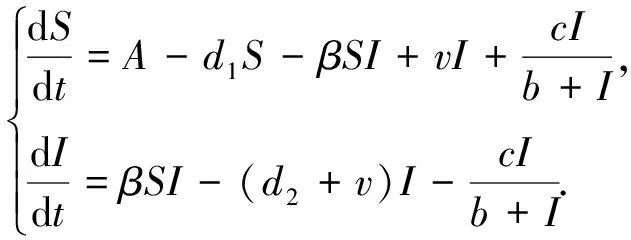
(1)

作者利用稳定性和分支理论，研究了平衡点的存在性、 稳定性、 后向分支和Hopf分支等[1]. 文献[2-12]深入研究了具有饱和治疗函数的传染病模型. 这些模型的人口输入均是常数输入，这与实际情况不是很吻合. 因此，本文基于Logistic出生和饱和治疗项提出以下模型：

(2)

式中：S(t)，I(t)分别为t时刻的易感者和染病者数量；r为内禀增长率；k为环境容纳量；β为有效接触率；μ为自然恢复率；c为单位时间内的最大治疗量；b用来衡量饱和发生的时间，满足h(b)=c/2；d为染病者的死亡率； 所有参数都是正的.

本文主要研究模型(2)的可行域和平衡点的存在性、 稳定性，以及模型的Hopf分支和B-T分支，并通过数值模拟来验证理论结果.

1 模型的基本结果

根据模型(2)的第1个方程，可以得到

对上述不等式积分，并代入初始条件，得

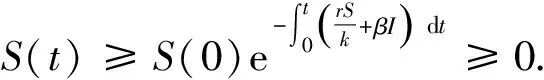
类似地，根据模型(2)的第2个方程，可以得到

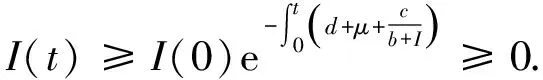
因此，模型的解都是正的. 接下来考虑模型解的有界性，首先把模型(2)的两个方程相加得到

对于任意的实数λ，有

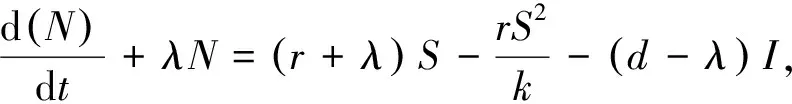
其中，N=S+I.选择一个正数λ，使得d-λ>0. 然后有

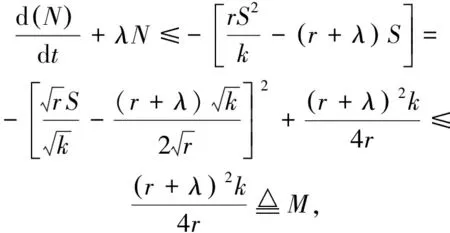
(3)

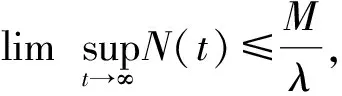
定理1模型(2)的正不变集为

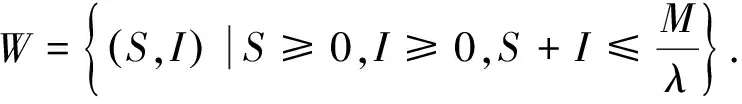
模型(2)有一个无病平衡点E0=(S0,0)=(k,0). 根据下一代生成矩阵[13]，模型的基本再生数为

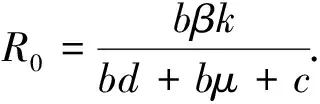
(4)

正平衡点满足下列方程

(5)

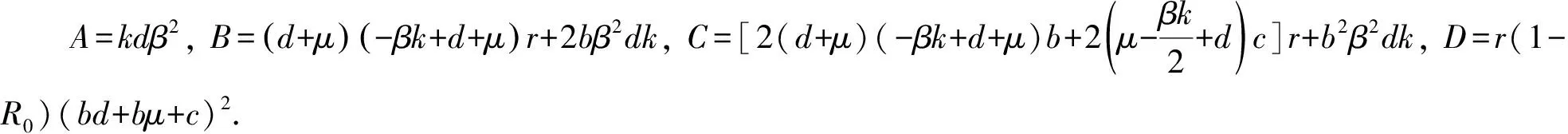
令A1=B2-3AC，B1=BC-9AD，C1=C2-3BD，定义Δ是g(I)关于I的判别式.

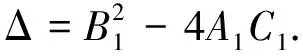
引理1当R0≥1时，如果C>0那么B>0.

d+μ)cr+4(μ+d)(-βk+d+μ)r≥

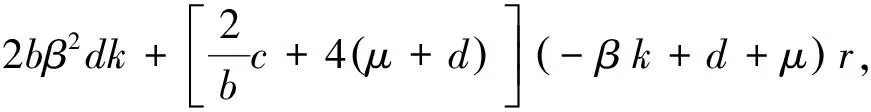
B=2bβ2dk+(μ+d)(-βk+d+μ)r≥mC.

根据引理1可以得到：

1) 当R0>1，C>0，B>0；C<0，B>0或C<0，B<0时，模型存在一个正平衡点.

2) 当R0=1，C>0，B>0时，模型不存在正平衡点；C<0时，模型存在一个正平衡点.

3) 当R0<1，C>0，B>0时，模型不存在正平衡点；C<0时，有下列几种情况：

a) 当Δ>0时，模型不存在正平衡点.

b) 当Δ<0时，模型存在两个正平衡点.

c) 当Δ=0时，模型存在一个正平衡点.

根据以上分析，有以下定理：

定理2对于模型(2)而言，无病平衡点E0始终存在.当R0>1时，模型存在唯一的正平衡点E1(S1,I1)； 当R0=1，C<0时，模型存在唯一的正平衡点E2(S2,I2)； 当R0<1，C<0，Δ<0时，模型存在两个正平衡点E3(S3,I3)，E4(S4,I4)，且当Δ=0时，两个正平衡点重合为一个正平衡点E*.

2 平衡点的稳定性

2.1 无病平衡点的稳定性

在无病平衡点E0(k,0)处，模型(2)的Jacobian矩阵为

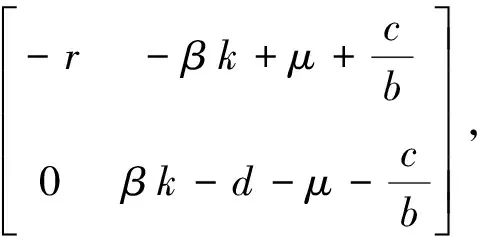
特征方程为

(6)

通过分析，可以得到以下定理：

定理3当R0<1时，无病平衡点是局部渐近稳定的； 当R0>1时，无病平衡点是不稳定的.

2.2 正平衡点的稳定性

模型(2)在正平衡点E(S,I)的Jacobian矩阵为

特征方程为

λ2-tr(JE)λ+det(JE)=0.

(7)

根据模型(2)的第2个方程，得

((βb2-2rb-c)k+4rbS)I-b2r(k-2S))，

Idkβ(b+I)2+(-2βS+2d+2μ)Ib)+

I2(-βS+d+μ)(k-2S)r)=βIg′(I),

其中,g′(I)=3AI2+2BI+C，A>0.因此，有以下几种情况：

1) 当R0>1时，存在一个正平衡点E1，当R0=1时，存在一个正平衡点E2.在Ei(i=1,2)处，g′(Ii)>0，det(JEi)>0，当tr(JEi)<0时，Ei是局部渐近稳定的； tr(JEi)>0时，Ei是不稳定的.

2) 当R0<1时，在E3处，g′(I3)<0，det(JE3)<0，则E3是一个鞍点.在E4处，g′(I4)>0，det(JE4)>0，当tr(JE4)<0时，E4是局部渐近稳定的； 当tr(JE4)>0时，E4是不稳定的.于是，可得下面的定理：

定理4当R0>1时，存在一个正平衡点E1； 当R0=1时，存在一个正平衡点E2； 当tr(JEi)<0(i=1,2)时，Ei是稳定的结点或焦点； 当tr(JEi)>0时，Ei是不稳定的.当R0<1时，存在两个正平衡点E3和E4；E3是一个鞍点； 当tr(JE4)<0时，E4是稳定的结点或焦点； 当tr(JE4)>0时，E4是不稳定的.

3 分支分析

根据Sotomayor’s定理[14]，当R0=1时，如果cr≠βb2d，模型会发生跨临界分支； 如果cr=βb2d，模型会发生叉形分支.根据文献[15]的方法，当R0=1时，如果cr>βb2d，模型会发生后向分支. 接下来研究Hopf分支以及尖点分支.

3.1 Hopf分支

在正平衡点Ei(i=1,2,4)处，当tr(JEi)=0时，模型可能会发生Hopf分支，令x=S-S*，y=I-I*，将模型(2)在原点泰勒展开可得

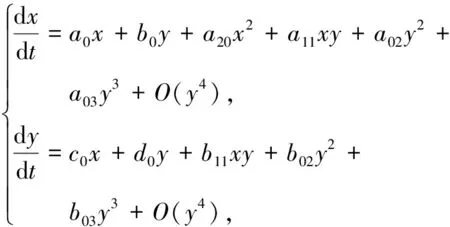
(8)

其中

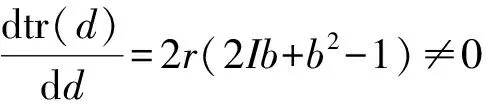
其中，Δ=a0d0-b0c0=det(JE2)>0，可以得到下面的定理：

定理5对于模型(2)，当σ<0时，模型发生超临界Hopf分支； 当σ>0时，模型发生亚临界Hopf分支； 当σ=0时，模型发生Bautin分支.

3.2 尖点分支

由定理2的分析可知，当Δ=0时，两个正平衡点E3和E4合并为一个正平衡点E*，此时det(E*)=0.如果tr(E*)=0，正平衡点的特征方程有两个零特征值，模型(2)会发生B-T分支.

定理6正平衡点E*是一个余维2的尖点，也是一个B-T分支点.

证明令x=S-S*，y=I-I*，然后将模型(2) 在原点泰勒展开成式(8)，同时作变换X=x，Y=a0x+b0y，可以得到

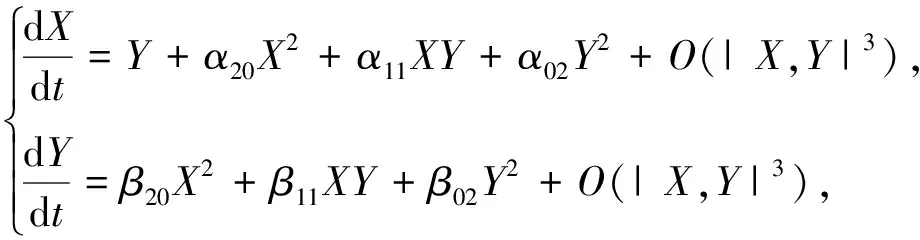
(9)

其中

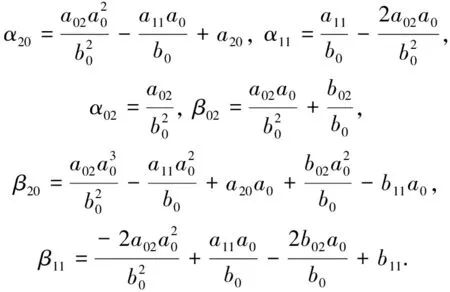
作近似恒等变换

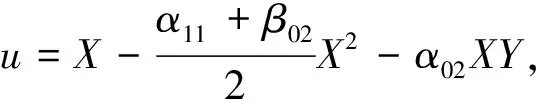
v=Y+α20X2-β02XY.

可以得到

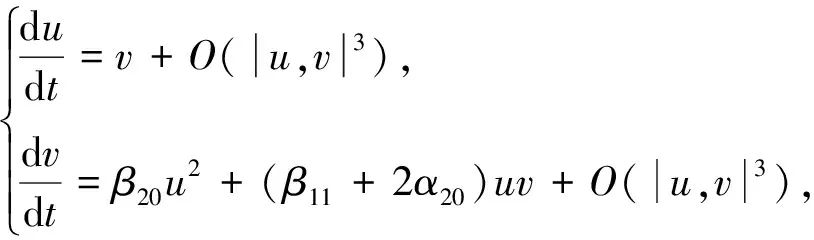
(10)

因此，当β11+2α20≠0时，E*是一个余维2尖点，当β11+2α20=0时，至少是余维3的.

4 数值模拟

为了验证正平衡点的存在性，取r=0.05，k=20，β=0.033，μ=0.001，c=0.027，b=0.1，绘制I随R0变化的曲线.由图 1 可以看出，正平衡点的个数随着R0的变化而变化.当R0较小时，模型不存在正平衡点； 当R0=0.858时，模型存在一个正平衡点； 当R0取值在0.858～1之间时，模型存在两个正平衡点； 当R0≥1时，模型存在一个正平衡点.

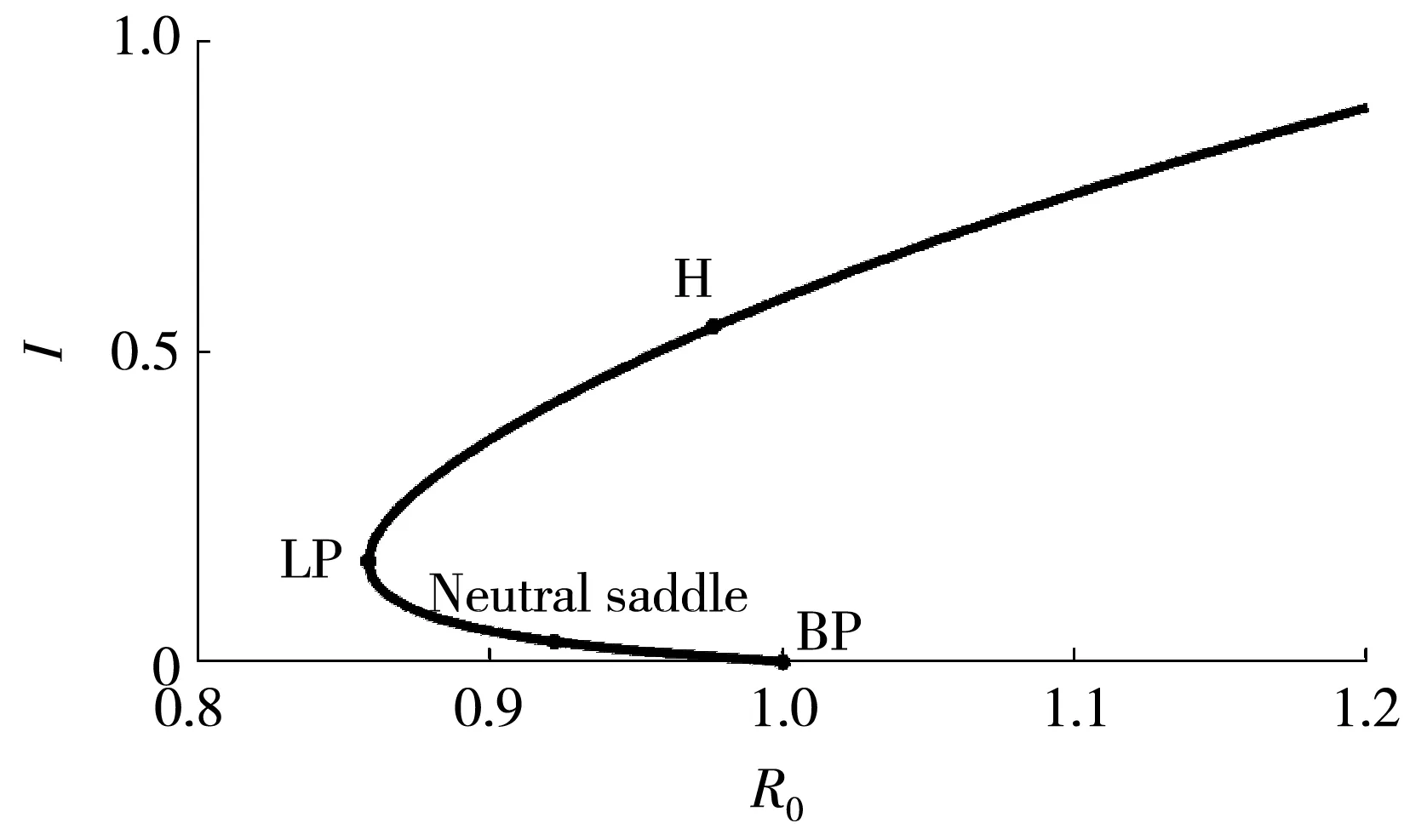
图 1 模型(2)平衡点个数随R0变化的分支图

下面验证Hopf分支以及极限环的存在性，选择第1个Hopf分支点作为初始点，以R0为分支参数，绘制极限环曲线，如图 2 所示.

图 2 以第1个Hopf分支点为初始点的分支图

由图 2 可以看出，在第1个Hopf分支点附近形成一个不稳定的极限环且在第2个Hopf分支点附近消失.

然后，以第3个Hopf分支点为初始点，以R0作为分支参数，绘制极限环曲线，如图 3 所示. 由图 3 可以看出，在第3个Hopf分支点附近形成一个不稳定极限环后趋于稳定，最后消失.

图 3 以第3个Hopf分支点为初始点的分支图

固定参数r=0.027 412 217，k=20，μ=0.001，c=0.5，b=0.2，d=0.027，随着参数β的变化模型会发生倍周期分支，如图 4 所示.

图 4 模型(2)的倍周期分支曲线图

选择r，c作为分支参数，固定参数k=20，μ=0.001，b=2，d=0.027，模型会随着分支参数的变化出现Bautin分支GH点、 B-T分支点以及尖分支CP点，如图 5 和图 6 所示.

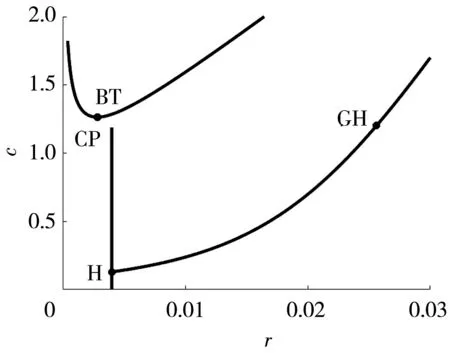
图 5 模型(2)的Bautin分支及B-T分支曲线图

图 6 图5中BT点以及CP点的局部放大图

以上数值模拟验证了理论结果，变化的人口模型具有更加复杂的分支现象.

5 结 论

基于文献[1]中的传染病动力学模型，本文考虑logistic增长率和饱和治疗项，建立了一个新的SIS传染病模型. 首先确定了模型的可行域和基本再生数，分析发现模型正平衡点的个数会随着R0的变化发生改变； 其次，分析了平衡点的稳定性，利用规范型理论，研究模型出现的分支现象，发现模型不仅出现余维1的跨临界、 叉形、 后向和Hopf分支，还会出现Bautin分支和至少余维2的尖点. 通过数值模拟发现，模型经历了倍周期分支和B-T分支. 分析结果拓展了人们对疾病控制影响因素的认识，在控制长期传播的传染病时，不仅要考虑到医疗资源的限制，而且要充分考虑人口增长的影响.