基于MAS的合作—竞争编队研究
2021-12-26纪志坚
王 潇,纪志坚
(青岛大学自动化学院,山东 青岛 266071)
0 引言
近年来,多智能体系统(MAS)的编队运动问题引起了国内外学者的广泛关注[1-2],与传统控制系统相比,多智能体系统具有巨大的优越性、可靠性、灵活性和对不确定环境的适应性。多智能体编队运动在自然界、工程实践和军事应用中都是重要的,从天体运动到电子运动,从动物的群集或训练行为到生物细胞运动,编队运动广泛存在于宏观和微观之中。
在自然界中,动物集体聚集通过避免捕食者和有效觅食而使同类动物受益。在自然现象的启发下,研究人员开发了一些重要的方法来实现一组智能体的编队运动。在开创性的工作中,Craig Reynolds建立了一个模拟的“Boids”模型,并提出3个行为规则:凝聚、分离、调整规则[3]。在过去的几年里,人们对编队控制问题进行了很多改进,目前编队控制方法主要可分为3类:基于行为法[4]、虚拟结构法[5-6]、领导者—跟随者法[7-13]。基于行为法通过调节权重以实现多智能体系统的最优编队控制,是从动物的群体行为中抽象出来的一种方法,此方法适用于分散控制,但在控制设计和稳定性分析方面存在困难。虚拟结构法由M.Anthony Lewis提出,将所有智能体视为单个实体,编队控制精度较高,此方法下编队队形可任意设定,但是很难确定虚拟参考点并传输其状态信息,很难实现编队中各智能体的信息同步。在这3类多智能体系统编队控制方法中,领导者—跟随者法最为流行,由于其方便、易分析、易实现而在多智能体编队控制问题中得到了广泛的研究[14]。在领导者—跟随者方法中,领导者是明确的和突出的[15],指定一些智能体作为领导者,其余智能体为跟随者,通过控制协议引导跟随者与相应的领导者保持所需的相对位置和方向,在本文中主要研究了基于领导者—跟随者方法的多智能体编队控制问题。
在上述参考文献中,智能体通常与一些简单的控制协议互连,通过合作关系交换信息来实现和保持期望的编队。也就是说,多智能体系统的通信权值是非负的,事实上,合作与竞争在自然界与社会制度中广泛存在,有些智能体可能会合作,而另一些智能体则会反对[16-17]。然而,对于具有合作—竞争关系的智能体,在编队控制方面几乎没有结果,这可能是未来战场的潜在应用。本文首先利用有向符号图提出了具有合作—竞争关系的多智能体系统的编队控制问题,然后为每一个智能体设计编队控制算法,以实现期望的编队队形。
本文符号:Rn和Rn×n分别表示n维欧氏空间和n×n实矩阵的集合。In是n×n维单位矩阵,⊗表示克罗内克积。给定两个集合X和Y,XY表示其元素属于X但不属于Y的集合,C>0和C<0分别表示复平面的右半开平面和左半开平面。
1 预备知识
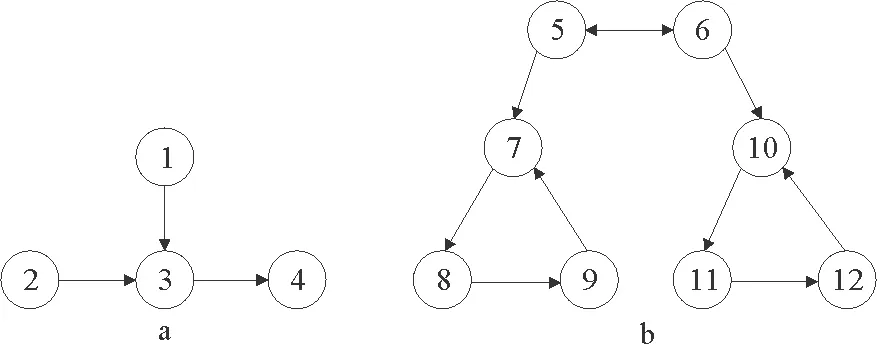
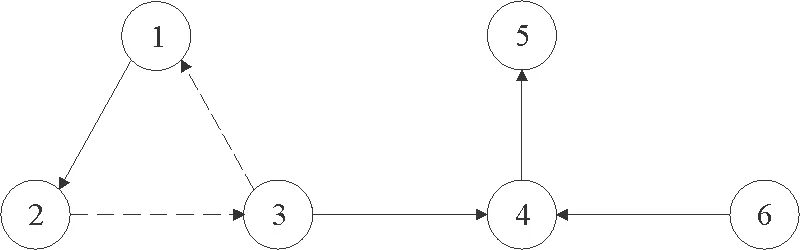
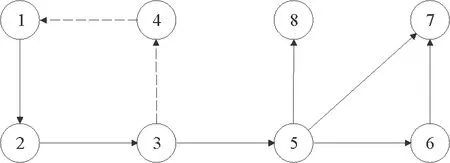
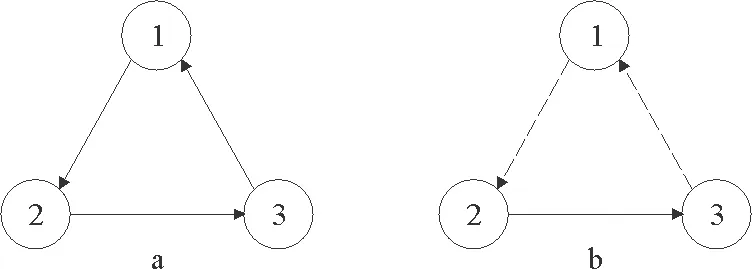
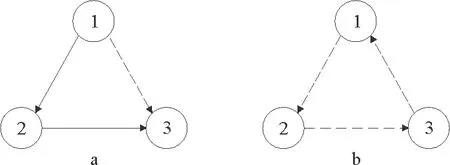
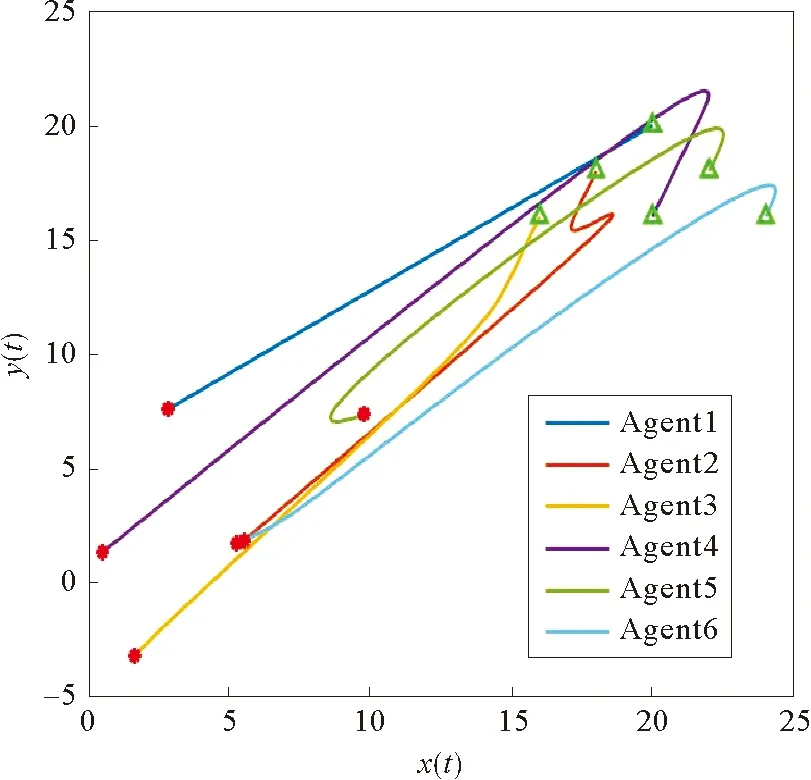
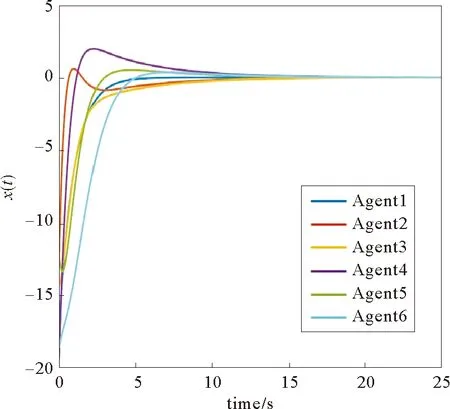
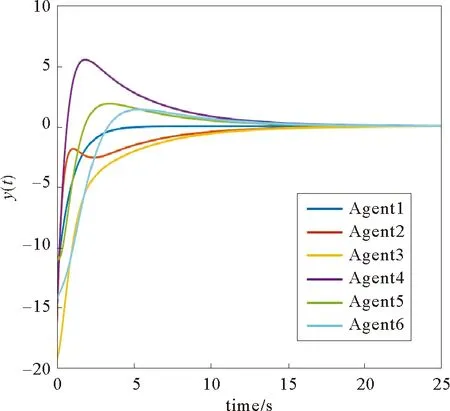
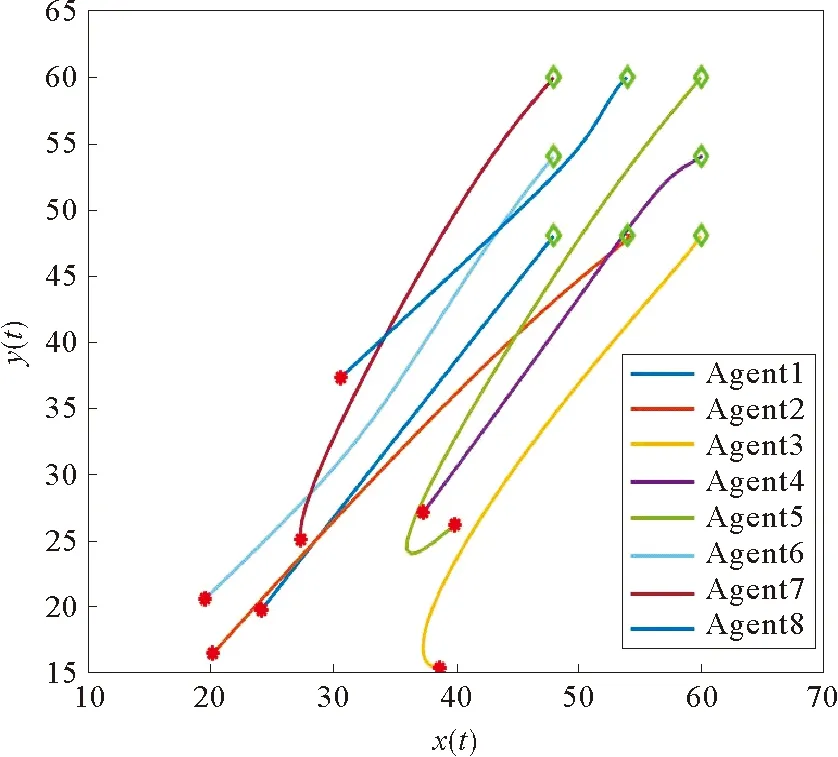
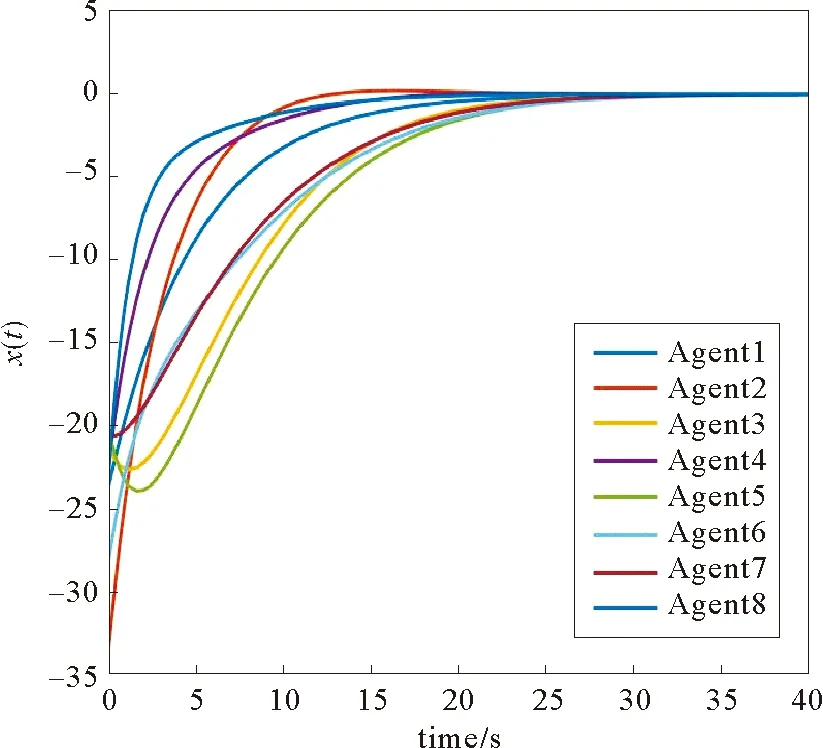
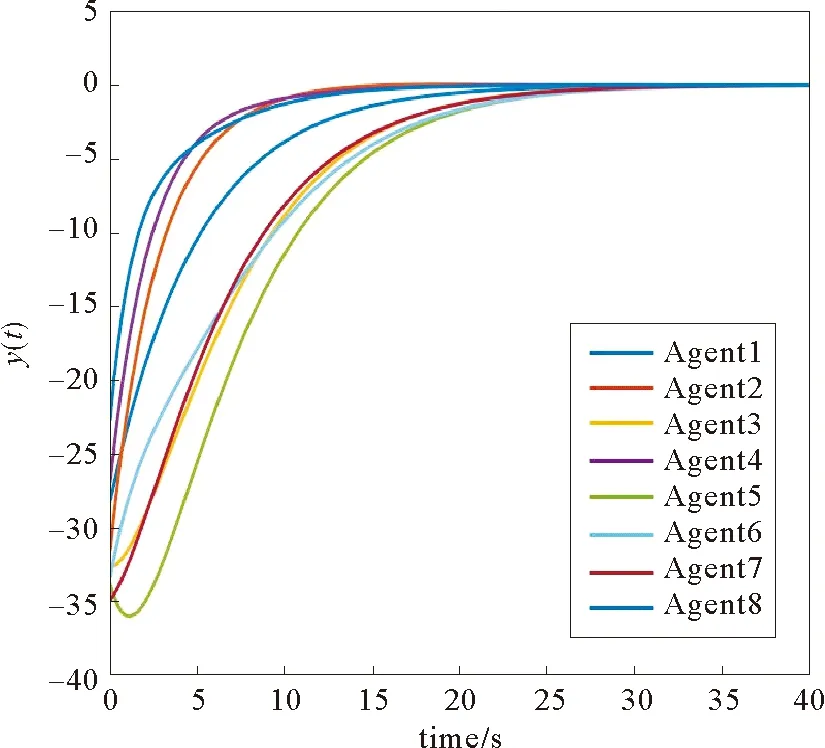
考虑一个由有向符号图G=(V,E,A)表示的多智能体网络,其中V={v1,…,vn}表示图的顶点集,边集E∈V×V表示智能体与智能体之间的交互。在有向图中,边是由两个顶点组成的有序对,(vi,vj)表示一条有向边,vi表示边的起点,vj表示边的终点,即(vi,vj)和(vj,vi)是两条不同的有向边。在有向图中,有向边也称为弧,始点称为弧尾,终点称为弧头。有向图G中eij=(vj,vi)∈E,则称顶点vj为vi的邻居,vi的邻居集合可以表示为Ni={vj∈N:eij=(vj,vi)∈E,j≠i}。如果(vi,vi)∈E,则称有向图G带有自环。没有多重边结构以及环结构的图称为简单图,本文研究的都为简单图。在有向图G中,如果对于每一对vi、vj,vi≠vj,从vi到vj和从vj到vi都存在路径,则称图G是强连通图。对于有向图,将所有的有向边替换为无向边,所得到的图称为原图的基础图,如果一个有向图的基础图是连通图,则有向图被称为弱连通图。将多智能体个体按照是否接受外部控制输入分为领导者与跟随者,领导者集合表示为Vl={v1,v2,…,vm},并且满足v1 图G的邻接矩阵A=[aij]∈Rn×n描述一个图节点之间的信息交流,定义为 (1) 其中,wij表示边的权重,本文中wij:E→{±1}用正或者负权重来捕获智能体之间的合作和竞争关系。具体地说,如果wij=1,vj称为vi的正邻居;如果wij=-1,则称vj是vi的负邻居,其中正邻居表示合作交互,而负邻居表示vj和vi的竞争交互。 有向图G的拉普拉斯矩阵L=(lij)定义为 (2) 有向图G中的度矩阵定义为Δ=[Δij],其中当i=j时,Δ=ID(vi);否则,Δij=0。由此可见,图G的拉普拉斯矩阵可以表示为 L=Δ-A (3) 如图1所示,每个圆圈中的数字表示节点集N={1,2,…,12}中的节点。为了简洁起见,省略了拓扑图的权重。图中有3个独立强连通分量,由节点集{1}、{2}和{5,6}诱导组成。有向图中的极大强连通子图称作为有向图的强连通分量(SCC),一个图的极大强连通子图加入任何一个不在它点集中的点都会导致它不再强连通,值得 图1 12节点拓扑图 注意的是,由节点集{7,8,9}、{10,11,12}诱导的并不是iSCC而是SCC。由于有向图的一个顶点构成一个强连通分量,所以任何有向图都包含最多m(1≤m≤n)个独立强连通分量。 引理1[18]假设方阵A是不可约矩阵,D是对角矩阵。那么A+D也是不可约矩阵。 引理2[18]A=[aij]∈Rn×n是图G的邻接矩阵,假设λ是A的特征值,满足不等式: 如果图G是强连通的,则: 1)每个盖尔圆通过λ, 引理3[19]假设有向图G=(N,E,A)是弱连通的,L是G的拉普拉斯矩阵。当且仅当G=(N,E,A)包含m个独立强连通分量时,则Rank(L)=n-m。 如何实现多智能体系统的合作—竞争编队运动,具有重要的理论和现实意义,但同时也是当前我们面临的一大挑战。本文试图对这一复杂问题进行研究。为了便于描述,我们在这里研究了6个和8个多智能体系统的合作—竞争编队运动。 考虑由n个智能体组成的多智能体系统,每个智能体都被看作是有向图G中的一个节点。每条边(vi,vj)∈E对应于智能体之间的信息传递通道,假设第i个智能体具有式(4)的动力学方程: (4) 其中xi∈Rn代表多智能体的状态,ui称为控制协议。设Vl={i1,…,im}是有外部控制输入的领导者集合,Vf代表剩余的多智能体集合,即跟随者集合。每个智能体i的动力学为 (5) 其中ri是多智能体系统的外部控制输入。 图2 6智能体合作—竞争交互网络 图3 8智能体合作—竞争交互网络 该6个和8个智能体构成合作—竞争交互网络,用有符号图G=(V,E,A)来描述。在图2和图3中,实线边和虚线边分别表示智能体的合作关系和竞争关系。为了方便起见,我们使用正、负权值来描述有符号图理论中的这种关系。 在编队控制问题中,一个编队目标向量di∈Rn从一开始就被分配给每个智能体i∈V。变量di-dj可以表示智能体i和智能体j的相对编队向量,它与参考坐标无关。所有的智能体都必须通过收集邻居的信息来转移到想要的位置。当多智能体系统中所有智能体的状态满足: (6) 我们认为合作—竞争编队形成。 在农场中,牧羊犬必须让羊群远离庄稼,牧羊犬观察羊群的行为在绵羊看来可能是一种对立竞争的行为。在这种对抗行为下,牧羊犬和羊群可以形成牧羊人所期望的形态。根据此局部交互规则,智能体i的编队控制ui(t)设计如式(7): (7) 其中,Ni是智能体i的邻居集,aij≠0是有限集合中的加权因子。B=diag(b1,b2,…,bN)为外部控制输入矩阵,这里: (8) bi=1表示外部控制输入ri作用于智能体i,否则bi=0。外部控制输入ri设计如式(9): ri=-Ki(xi-di) (9) 因此,多智能体i的动力学可修改为 (10) (11) (12) 定义2[20]如果一个有符号图G的节点集可以划分为两个不相交的子集,其中一个子集可以是空集。使得同一子集中的两个节点aij≥0,而不同子集中的两个节点的aij≤0,则称图G为结构平衡;否则就是结构不平衡。 虚线代表负加权边。图4 两个结构平衡的有向图 虚线代表负加权边。图5 两个结构不平衡的有向图 一个有向图G中的极大强连通子图称为有向图的独立强连通分量(iSCC)。如果iSCC是结构平衡的,则有符号图G的独立强连通分量被称为结构平衡的独立强连通分量(SBiSCC)。否则,iSCC被称为结构不平衡的独立强连通分量(SUiSCC)。 定理1假设有向符号图G是弱连通的,图G包含c个不同的结构平衡的独立强连通分量,则结构平衡的独立强连通分量的拓扑图Gs=(Vs,Es),s∈Nc。当且仅当Vl∩Vs≠φ,由动力学(5)和控制协议(7)控制的多智能体系统是稳定的,即多智能体系统中的所有智能体的状态满足式(6),可以形成期望的合作—竞争编队运动。此外,接收外部控制输入的最小节点数等于结构平衡的独立强连通分量的数目。 证明:注意有符号图的稳定性问题不同于无符号图的稳定性问题。由于有符号图G包含c个不同的结构平衡的独立强连通分量,在不丧失一般性的情况下,假设(11)的L和D是 例1考虑一个具有xi:=(xi1,xi2)∈R2的多智能体系统,由6个节点的有符号有向图表示,如图2所示。我们已经知道这个图中有2个结构平衡的独立强连通分量,将节点1和节点6被选择为领导者,其余节点为跟随者。图2的拉普拉斯矩阵为 假设所有智能体的初始位置都是随机选择的,分散的外部控制输入可以作为r1=-(x1-d1)和r6=-(x6-d6)。多智能体系统的目标是获得一个三角形的编队队形,其中位置矢量被假定为 虽然多智能体的初始位置是随机选择的,但多智能体可以实现三角形的编队队形,如图6所示。 注:星号和三角形分别表示t=0 s和t=20 s时多智能体系统的位置。图6 6智能体三角形编队队形图 图7 6个智能体x轴方向位置差 例2考虑一个具有xi=(xi1,xi2)∈R2的多智能体系统,由8个节点的有向符号图表示,如图3所示。我们已知这个图中有1个SBiSCC,选择节点4作为领导者,其余节点作为跟随者。图3的拉普拉斯矩阵为 假设所有智能体的初始位置都是随机选择的,分散的外部控制输入可以为r4=-(x4-d4)。多智能体的目标是获得一个具有矩形形状的编队队形,其中期望位置矢量被定义为 图8 6个智能体y轴方向位置差 注:星号和菱形分别表示t=0 s和t=40 s时多智能体系统的位置。图9 8智能体矩形编队队形图 图10 8个智能体x轴方向位置差Fig.10 Position difference in x-axis direction of eight agents 图11 8个智能体y轴方向位置差 本文基于牧羊犬与羊群的自然现象研究了多智能体系统新的编队控制问题。基于有向符号图,针对每个智能体提出了一种分布式编队控制算法,实现了多智能体系统的合作—竞争编队运动。利用结构平衡的独立强连通分量推导出了一个充分条件,以确保所有智能体以分布方式进行合作—竞争编队运动,达到期望的编队队形。最后,通过数值仿真验证了理论结果的有效性。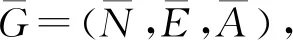
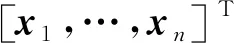
2 MAS编队控制协议
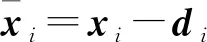
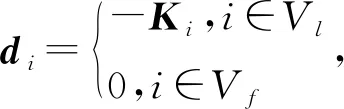
3 MAS编队稳定性
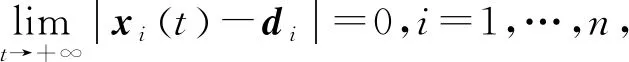
4 数值仿真

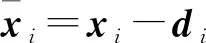

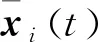
5 结论
