疫情事件下多灾点应急资源最优化配置研究
2021-12-26王付宇涛a艳a王小牛
王付宇,汤 涛a,李 艳a,王小牛
(1.安徽工业大学 a.管理科学与工程学院 b.复杂系统多学科管理与控制安徽普通高校重点实验室,安徽 马鞍山 243002; 2.马鞍山市人民医院普外科,安徽 马鞍山 243000)
0 引言
灾难的发生,给国家和人民生命健康造成了严重的威胁。如:2003年爆发的SARS疫情,造成了包括医务人员在内的多名患者死亡。2008年5月12日的汶川地震,造成了69 227人死亡,374 643人受伤,17 923人失踪[1]。此次新冠肺炎疫情的爆发对国家经济和人民安全造成了极大损失与威胁[2]。在灾难发生后,应急救援物资是疫情防控的重要基础,这对物资稀缺且急需援助的灾区来说非常重要。新冠疫情具有大规模传染性、潜伏性等特点,对物资的需求更为迫切。目前许多研究力求在尽可能短时间内将物资运达灾区,减轻灾害带来的损失。因此,如何在疫情发生初期快速支援灾区,救援病患,防止情况恶化,显得尤为重要。
应急物资调度一直是众多学者关注的研究热点[3-4],Jincheng等[5]把时间、路径可行性加入模型中,提出一种带有车辆调度的应急物资模型来解决物资调度问题;葛洪磊等[6]提出基于区域灾害系统理论来构建复杂灾害情景,建立了一个两阶段随机规划模型,针对不同灾害情景下对应急物资分配预案的制定。杜雪灵等[7]提出了考虑公平性的应急物资分配模型,设计了带有多个救援目标的应急调度模型。王付宇等[8]将灾难发生后的伤员进行分类,确定伤员需求综合权重值,建立以总救援时间最短和相对综合救援权重值最大为目标的应急救援模型。王旭坪等[9]在借鉴前景理论的基础上,建立应急响应时间的感知满意度函数,构建了一个多目标整数规划模型,以此来解决灾区应急物资分配问题。灾区信息是变化莫测的,詹沙磊等[10]提出灾区信息更新的应急物资规划模型,为解决灾点应急物资配送问题提供了精确的科学方法。为了提高应急救援效率与减少消耗成本,沈晓冰等[11]提出应急物资需求不确定情况下多目标规划模型。戴君等[12]考虑到配送中心定位与配送路径之间是相互影响的,建立了灾后应急物资配送的LRP模型。这些文献的研究大多是针对地震及其他自然灾害所进行的物资分配,以上文献研究中只是考虑物资如何经济地分配,没有考虑到灾区的紧急情况。传染病爆发后,每个灾点的受灾程度不同,并且灾区物资需求量很大程度上与现有的确诊感染人数有关,如何去衡量传染病灾区实际的紧急情况去分配物资是本文研究的主要问题。
人工蜂群算法(Artificial Bee Colony Algorithm,ABC)是新型仿生智能优化算法,具有参数设置简单、易操作等优点,但易陷入局部最优且易早熟收敛[13]。许多学者针对蜂群算法的缺点提出了一系列改进措施[14-16]。单娴等[17]为了提高蜂群初始解的质量,提出了一种基于复数编码的多策略人工蜂群算法。曹知奥等[18]为了使蜂群算法适用于非线性特征模型,提出了交叉-变异的人工蜂群算法。张架鹏等[19]为了解决同类机调度问题,设计了一种改进离散人工蜂群算法。赵明等[20]将反向学习策略和广泛学习策略融合到蜜蜂的搜索过程,提出了一种改进的蜂群算法。
根据新冠疫情传播的特殊性,可以将疫情事件下应急物资的精准配置归纳为两个重要特点:1)疫情初期,需要量化灾区的实际紧急情况,灾区具有异质性,不同的灾区受灾情况不同;2)物资的需求量在很大程度上与已确诊的感染人数息息相关,需要事先根据灾区感染人数预测灾区需求量。
针对上述特点,本文基于各个灾区的感染人数数据,选择历史数据的某一个时刻作为基点,根据基点数据利用SEIR模型预测出决策时刻各个灾区的感染人数,以此求出各个灾区的紧急程度权重、预测出其物资需求量;构建时间满意度最大化、应急物资供给公平化与总成本最小化的多目标应急调度模型;为求解该多目标应急调度问题,将非支配排序思想引入蜂群算法,设计了多目标优化蜂群算法。
1 应急物资配置多目标优化模型构建
1.1 问题描述
新冠疫情发生后,由于具有传染性,需要及时配送物资以防灾区情况继续恶化。确诊感染人数几乎决定了物资的需求量,为了更好地衡量各个灾区的紧急情况,本文以各个灾区感染人数占总感染人数的比例作为灾区紧急程度权重,根据实际紧急情况来分配救灾物资。构建了满意度最大化函数与分配公平化、总成本最小化函数,并且以该三个目标函数来对问题进行求解分析。
模型假设:
1)假设灾区对应急物资的需求量与灾区感染人数成正比关系;
2)假设灾区物资需求量以及救援中心的储备物资是可以预测的;
3)假设救援中心的物资储备量短时间内保持不变;
4)默认每个物资中心的物资储备相同且充足,相应灾点所需物资与物资中心一致,且物资中心储备具有可补充性。
假设传染病发生后,有n个严重的待救援灾区,每个灾区的物资需求量通过专门的机构预测确定。假设已确定m个应急救援中心来对这些灾区进行支援,由于各个灾区的感染人数不同,因此,基于感染人数构建了紧急程度权重,通过SEIR模型和历史数据确定当前决策时刻各个灾区的紧急权重,模型参数说明如下:
I:表示灾区集合,i=1,2,…,n;
J:表示应急救援中心集合,j=1,2,…,m;
Ri:表示灾区i的物资需求量;
ri:表示灾区i的单位感染人数物资需求量;
Gj:表示应急中心的物资供应量;
cij:表示应急中心j运送一个单位物资给灾区i的成本;
nij:表示应急中心j运送物资给灾区i的运送量;
xij:为0~1变量,应急中心j对灾区i进行支援,则xij=1,应急中心j不对灾区i进行支援,则xij=0;
tij:表示应急中心j与灾区i的广义时间距离;
St:表示t时刻易感人数;
Et:表示t时刻暴露人数;
It:表示t时刻感染人数;
Rt:表示t时刻恢复人数;
β:表示有效接触率;
k:表示暴露到感染发生率;
γ:表示康复率;
ωi:表示灾区i紧急权重。
1.2 确定紧急权重
考虑到每个灾区的紧急情况有所不同,提出紧急权重概念,根据感染人数来确定各个灾区的紧急权重ωi,选择过去某一时刻作为0时刻,利用SEIR模型在0时刻感染人数等数据基础上预测当前决策时刻感染人数,计算出各个灾区的紧急权重。
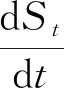
(1)
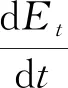
(2)
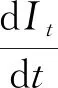
(3)
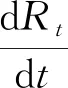
(4)
假设当前决策时刻为t,由于各个灾区感染人数的不同,为了求解该类物资分配问题,使物资尽可能公平地分配到各个灾区,为各灾区赋予一个紧急权重系数,紧急权重系数计算公式为
(5)
式中,ωi表示灾点i的紧急权重,Iti表示灾点i在t时刻感染人数。
灾区的物资需求量为
Ri=ri×Iti
(6)
1.3 时间满意度
在现有文献研究基础上,我们建立了基于紧急程度的时间满意度函数,在应急调度中,时间满意度是抽象的,本文利用救援时间偏离程度所表示的价值函数值衡量公众对救援时间的满意度。
(7)
定义灾区i的救援时间偏离度为
Ti=Tia-maxj∈J{xijtij}
(8)
时间满意度函数为
(9)
V(Ti)=-φ(Ti)b,Ti<0
(10)
式中,由于价值函数的斜率变化可知,在收益区间为凹函数,a小于等于1,在损失区间为凸函数,b小于等于1。根据风险厌恶原则,损失区间相对于收益区间的函数更为陡峭,φ>1。
(11)
1.4 分配公平性
本文为了使分配公平化,以所有灾点的物资满足程度的方差来衡量救援的公平性,所谓公平,就是使灾区人民受到同等的救援,在这里如果以物资量无差异,不足以衡量公平性,因为有些灾区受灾严重,物资需求量大,有些灾区则需求量小,因此,以物资满足程度指标来衡量公平。
(12)
(13)
(14)
式(12)表示灾点i物资满足程度,式(13)为所有灾点的平均物资满足程度,式(14)表示所有灾点物资满足程度方差最小化,方差值越小,表示差异越小,即分配越公平。
1.5 成本
在应急物资调度中,必须要考虑方案的成本,本文将成本函数定义为
(15)
1.6 最优化配置模型
(16)
(17)
(18)
(19)
(20)
ifxij=0→nij=0
(21)
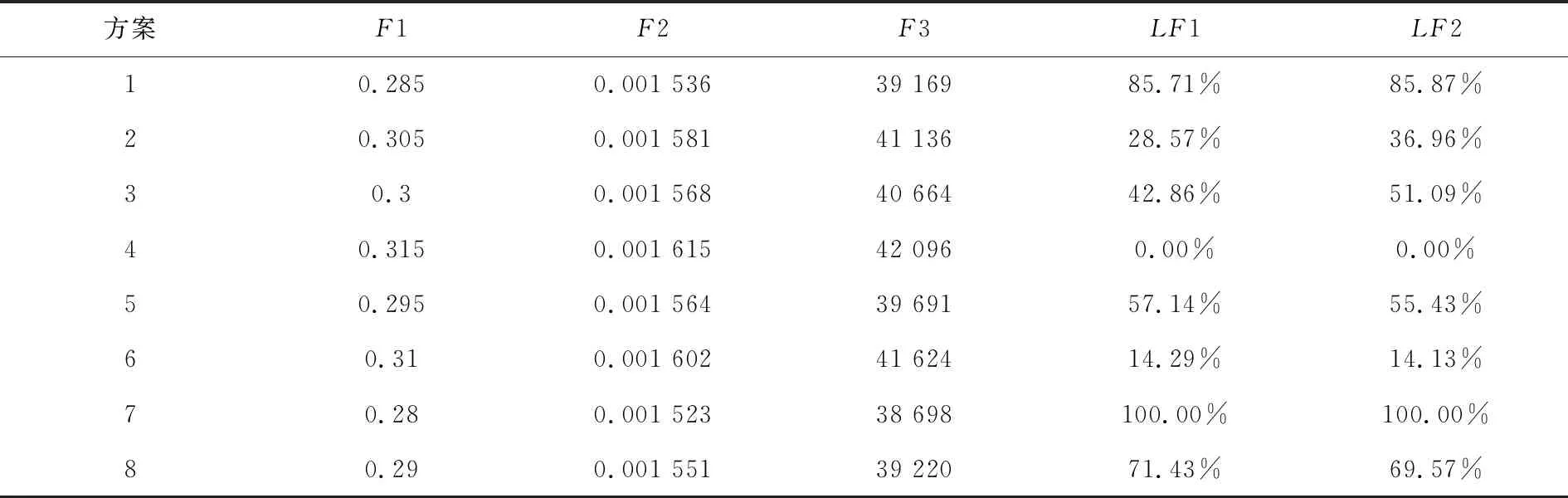
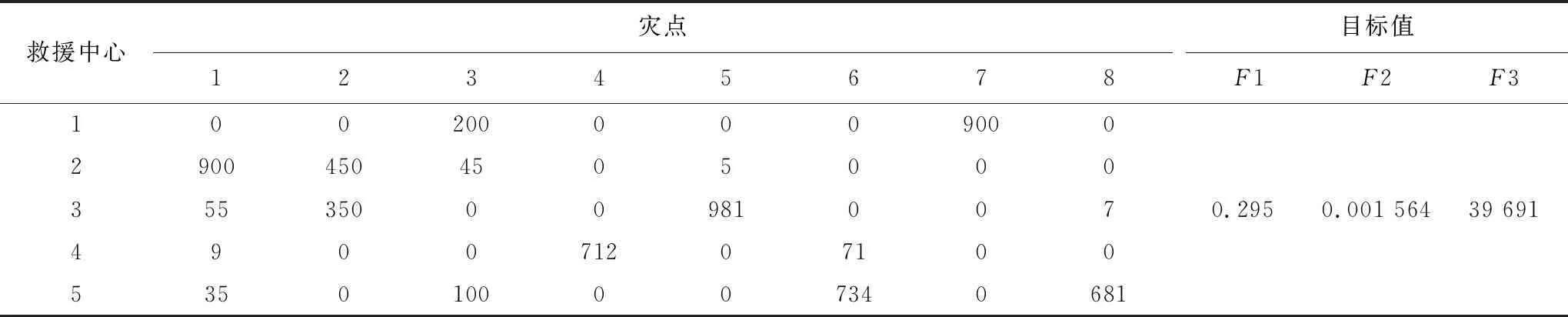
ifxij=1→0 (22) xij=0or1 (23) 式(16)、(17)、(18)表示三个目标函数,式(19)表示各个应急中心分配给灾点的物资量不超过其需求量;式(20)表示每个应急中心支援给各个灾点的物资量不超过其供应量;式(21)、(22)表示应急中心j支援灾点i,则xij=1,对应的nij取0到min(Ri,Gj)之间的数,否则xij=0,nij=0。 改进方式:引领蜂在初始解的领域内搜索新解时,φ系数是一个0到1之间的随机数,算法前期,使φ值较大,增加算法的全局搜索能力,在算法后期,逐渐逼近最优解时,此时使φ较小,φ的取值为 (24) 式中,t为当前迭代次数,maxgen为最大迭代次数,φmax为设置好的φ最大值,φmin为φ最小值。 由于是多目标问题,设计多目标蜂群算法,原始蜂群算法位置更新规则不再适用[21-22],因此,利用Pareto解来重新定义位置更新公式[23-24],在每次迭代时从Pareto解随机选择一个解,Xpareto表示随机选择解位置,此时蜂群位置更新公式为 Xi(t+1)=Xi(t)+φ×(Xpareto(t)-Xi(t)) (25) 教学思想变异扰动:由于搜索机制的单一,为了避免算法后期陷入局部最优,以一定概率去进行扰动: differentmeanf1=rand×(bestfitf1-TF×fitmeanf1) (26) differentmeanf2=rand×(bestfitf2-TF×fitmeanf2) (27) TF=round(1+rand) (28) Xi(t+1)=Xi(t)+differentmeanf1 (29) Xi(t+1)=Xi(t)+differentmeanf2 (30) 式中,differentmeanf1为目标函数1教学平均值,bestfitf1为解集里最好的f1值,TF为教学因子,round为四舍五入函数,rand为0~1之间随机数,fitmeanf1为种群平均f1值;differentmeanf2为目标函数2的教学平均值,bestfitf2为解集里最好的f2值,fitmeanf2为种群平均f2值。 步骤1:设置算法参数,最大迭代次数maxgen、种群大小SN、limit、φmax和φmin等,初始化种群; 步骤2:计算种群适应度值,初始筛选非劣解; 步骤3:计算参数φ,找出种群最优解,按照式(25)更新蜂群位置; 步骤4:跟随蜂阶段,计算适应度值,计算选择概率,选择较优个体,未被选择的个体按照式(25)重新更新位置; 步骤5:当有经过limit次循环,仍有未被更新的解,则放弃,重新生成; 步骤6:判断是否变异,若pm>rand,则随机选择式(29)或(30)更新位置; 步骤7:计算适应度值,更新Pareto解集,去掉重复个体; 步骤8:判断是否终止算法,若终止,则输出结果,否则,转步骤3。 Pareto得出的关于F1与F2、F3的一组解,如何确定其中一个合理的方案是一个问题,本文构建了F1得益指标LF1与F2损失指标LF2[25],借鉴参考文献[25],通过这两个指标以辅助决策者进行选择,在成本预算范围内去选择F1与F2满足条件的方案,决策者可根据自身对F1得益与F2损失的可接受程度选择满意的方案。 (31) (32) 式中,maxF1和maxF2为所有方案中F1和F2最大的值,minF1和minF2为所有方案中F1和F2最小的值,F1i为方案i的F1值,F2i为方案i的F2值。 假设由于疫情的爆发,造成了八个急需支援的灾点,现有五个可以支援灾点的应急救援中心,物资储存量分别为G1=1 200,G2=1 400,G3=2 000,G4=800,G5=1 600。考虑到疫情传播具有潜伏期,因此无法清楚了解灾难起始日,所以选取过去某一时刻作为起始时刻,灾点起始信息如表1所示,灾难发生后各救援中心开始快速响应,开展救援前的准备工作,在这里假设准备工作耗时两天,则令决策时刻t=2。 表1 灾点起始时刻信息表 在时间满意度函数里,根据参考文献[9],a取0.88,b取0.88,φ取2.25。各个应急中心到各个灾点的时间距离参数和成本参数如表2所示。 表2 时间距离与运输成本(tij/cij) 通过SEIR模型计算出两天后各个灾区的感染人数、紧急权重以及物资需求量,数据如表3所示。 表3 灾区当前信息 模型运行硬件环境为Intel(R)Core(TM) i7-1065G7@ 2.52 GHz双核处理器,RAM为8GB,软件环境为Window8操作系统64位,编程软件为Matlab R2014b软件。设置算法参数,种群大小为100,最大迭代次数maxgen为200,limit为100,φmax和φmin分别为2和0,为了客观比较算法之间的性能,几种算法相同参数取值相同,原始蜂群、NSGA-II、多目标粒子群种群大小均设为100,最大迭代次数均为200,对比结果如表4所示。 表4 改进蜂群与其他智能算法计算结果 四种算法的多目标Pareto分布如图1所示。 图1 四种算法Pareto分布 本文使用的算法性能评价指标分别是收敛性指标γ和分布性指标Δ,同文献[22]一样,由于真实最优Pareto未知,因此,本文将四种算法的全部运行结果的并集中的非支配解集近似为最优Pareto解集。 收敛性指标:用来评价所得解与真实最优解的逼近程度,如式(33)所示,N为所得Pareto集合中解的数量,di表示所得解集里第i个解与最优解集里最近解的距离,当γ值越小,代表算法收敛性越好。 (33) (34) 利用前面所得数据计算各种算法的收敛性指标与分布性指标,为了简化计算,只以F1与F2两个目标来计算指标,结果如表5所示。 表5 算法评价指标 由表5可得,从收敛性指标γ来看,改进蜂群算法要优于原始蜂群及其他对比算法,从分布性指标Δ来看,改进蜂群算法与对比算法无显著差异,略优于原始蜂群算法。 由于是多目标,设计了一种选择策略来辅助决策者在多目标蜂群结果中进行选择,假设成本预算为43 000,在预算范围内,F1得益指标与F2损失指标如表6所示。 表6 F1得益指标与F2损失指标 由表6可得,当决策者希望F1得益指标超过40%,F2损失指标低于55%,则可以选择方案4;如果决策者希望F1得益指标超过70%,F2损失指标低于70%,则可以选择方案8;在这里计算了F1得益率与F2损失率,具体如何选择,根据决策者对两个指标的可接受程度来决定。如决策者希望F1得益指标超过50%,F2损失指标低于60%时,选择方案5最为合适,方案5具体分配情况如表7所示。 由表7可得最佳分配方案为:应急中心1分配给灾点3物资量200个单位,灾点7物资量900个单位;应急中心2分配给灾点1物资量900个单位,灾点2物资量450个单位,灾点3物资量45个单位,灾点5物资量5个单位;应急中心3分配给灾点1物资量55个单位,灾点2物资量350个单位,灾点5物资量981个单位,灾点8物资量7个单位;应急中心4分配给灾点1物资量9个单位,灾点4物资量712个单位,灾点6物资量71个单位;应急中心5分配给灾点1物资量35个单位,灾点3物资量100个单位,灾点6物资量734个单位,灾点8物资量681个单位。 表7 方案5结果 使用SEIR模型对灾区感染人数进行预测后,可以快速根据灾区受灾情况进行物资的调度分配。从表4及表5的对比结果中可以看出,改进的多目标人工蜂群算法求解效果优于原始蜂群算法以及其他智能优化算法,表明改进算法在求解该类多目标优化问题时的可行性和优越性。 在新冠疫情爆发后,为了将应急医疗物资科学合理地从应急中心分配给各个受灾点,本文在SEIR模型预测各个灾区感染人数的基础上计算出了各灾点紧急权重,并预测出各灾点物资需求量;构建了时间满意度最大化、应急物资供给精准化与总成本最小化的多目标应急调度模型;为求解该多目标应急调度问题,将非支配排序思想引入蜂群算法,设计了多目标优化蜂群算法,并进行了算例验证。研究结果表明,本文提出的多目标优化模型适用于疫情事件下多灾点应急资源最优化配置问题,改进的人工蜂群算法较原始蜂群算法以及NSGA-II算法等具有更好的寻优效果。 然而,本文仅研究了如何根据感染人数预测各灾点物资需求量和如何分配物资,尚未与后续的运输车辆调度、车辆路径优化等问题相结合,因此,如何在紧急情况下进行应急医疗物资的精准配置与高效运输将是下一步的研究方向。2 改进多目标蜂群算法设计
2.1 改进蜂群算法
2.2 多目标蜂群算法步骤设计
2.3 选择策略
3 算例验证
3.1 参数设计
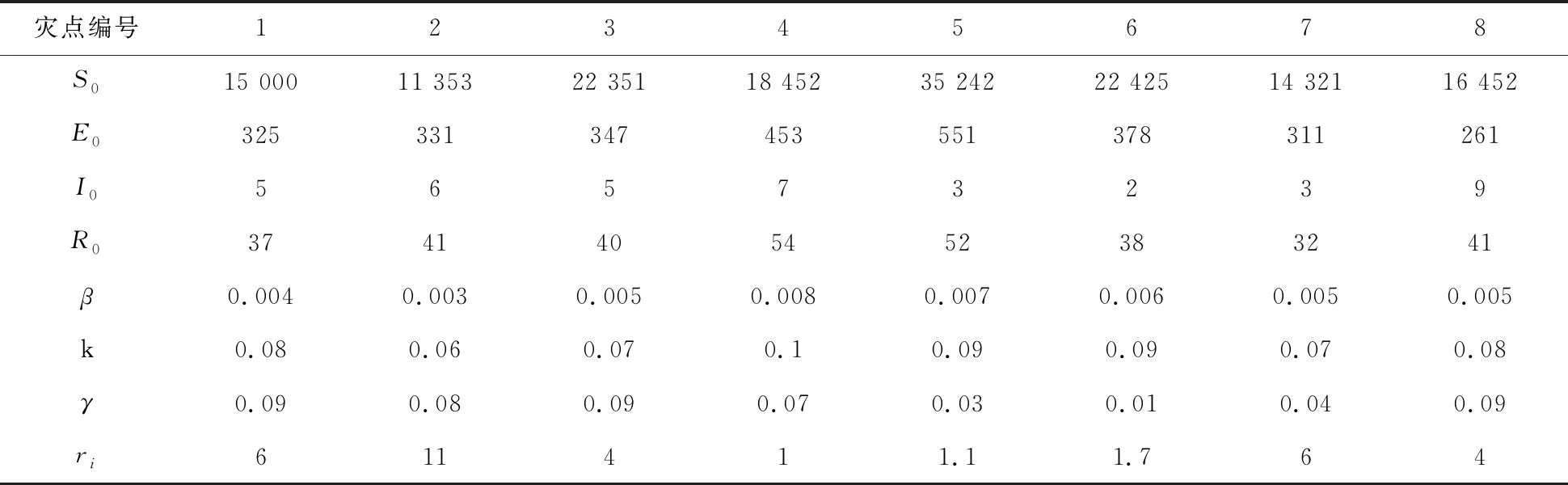
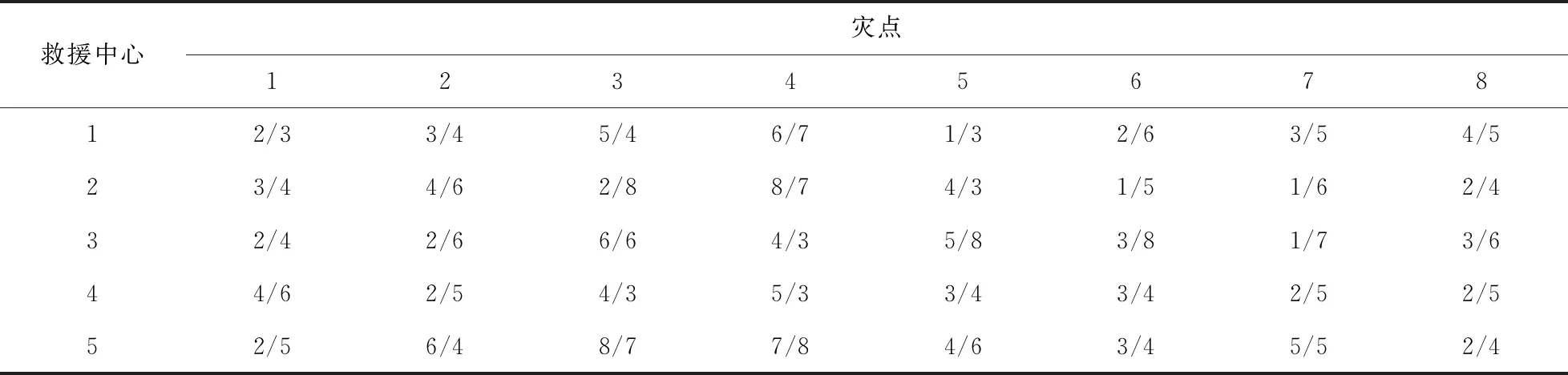
3.2 计算结果

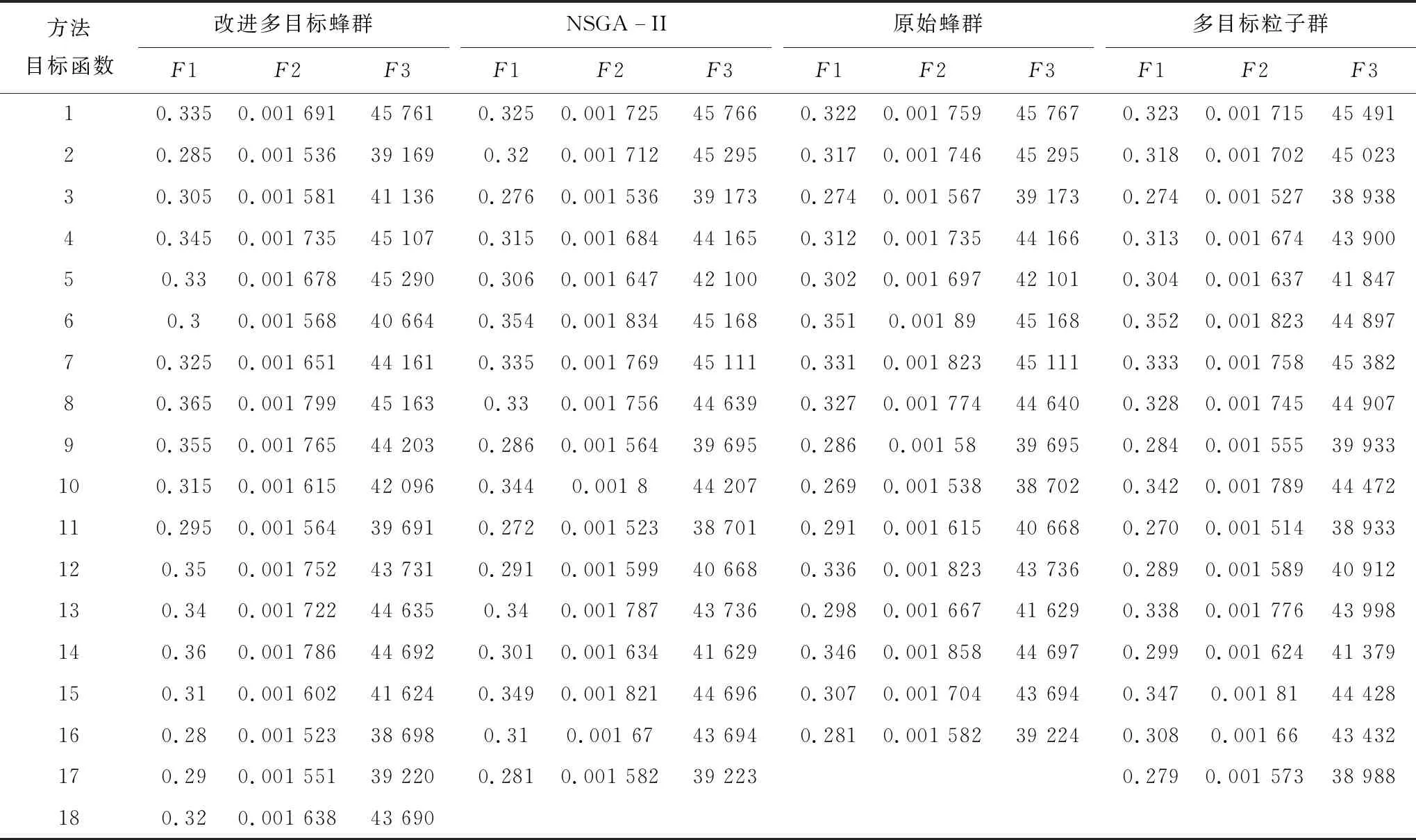
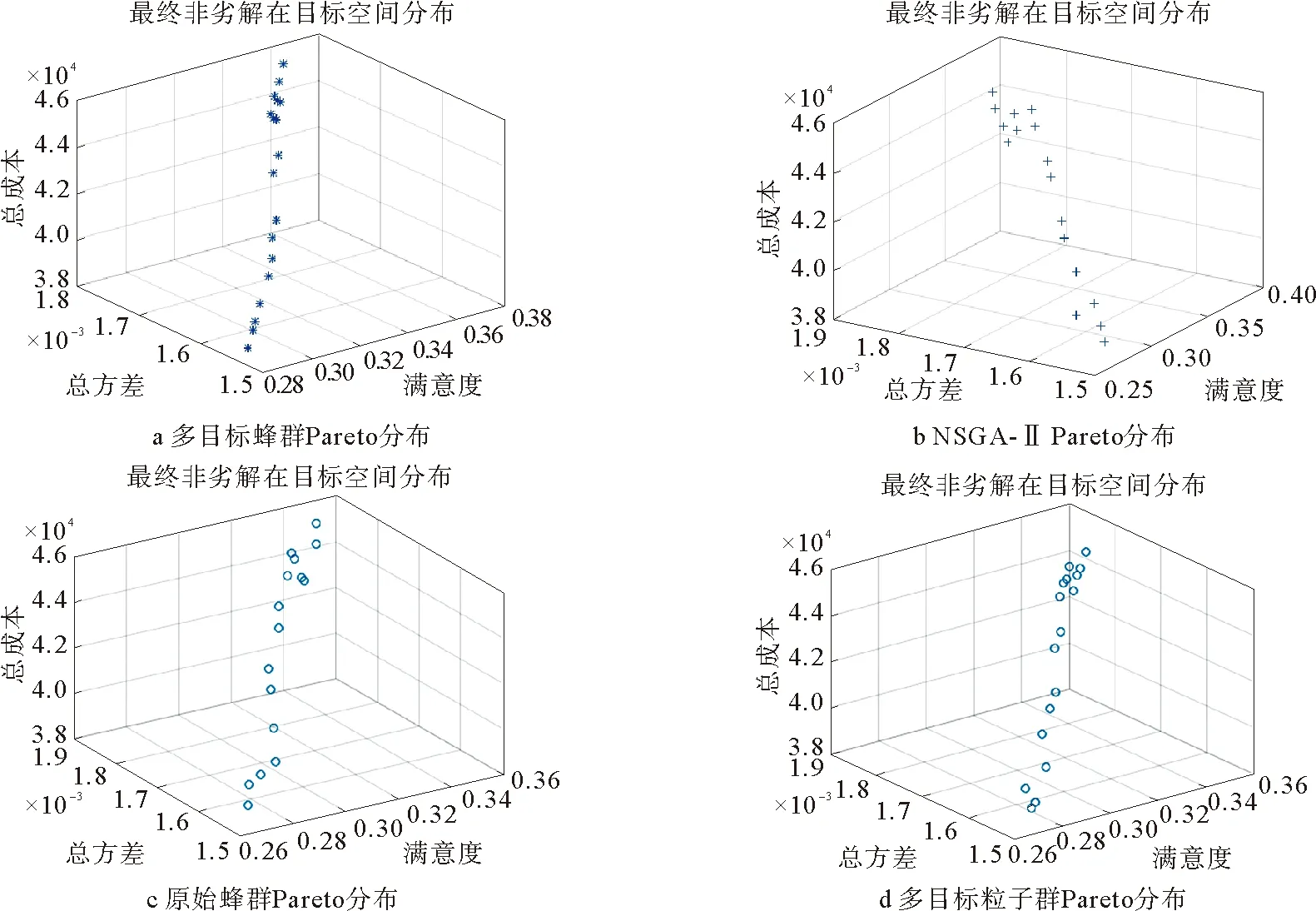
3.3 算法性能比较

3.4 选择方案
4 结论与展望
