基于改进Lagrange乘子法的交通信号配时优化研究

牟 亮，赵 红，崔翔宇，袁焕涛，李 燕，仇俊政

(青岛大学机电工程学院，山东 青岛 266071)

0 引言

交叉口的信号控制在交叉口通行效率、交通秩序以及污染物排放等方面有着重要的影响。近年来，全国机动车保有量不断增加，驾驶汽车已经成为人们日常的出行方式，我们也面临着交通堵塞和环境污染等严重问题。合理的交通信号配时方案可以有效地减少这方面的问题。交通排放会对环境甚至是人们的身体造成危害，人们也越来越关心出行时间。因此低排放和低延误成为交通信号控制的主要问题。现有文献表明，交通信号配时问题是复杂的、分布式的、混合的[1-5];交叉口的交通规律是难以预测的、复杂的、无规律的[6-9]，但VISSIM中可以较真实地反映出现实的交通运行情况。现实中在制定交通信号配时策略时不能仅考虑一方面，而是需要综合考虑多个方面，因此为提高交叉口的通行效率及降低环境污染，本文将采用多目标优化控制策略。多目标优化相较于单目标优化可以提高交叉口的综合性能，同时可以反映所研究的目标之间的关系，在实际工程问题中具有一定的优势。

目前国内外在Lagrange乘子法的研究上已经取得了一些成果。张克等[10]针对Lagrange乘子法将约束问题转化为无约束问题，与粒子群优化算法结合提出的一种新型算法；黄灿远[10]对Lagrange乘子法的乘子更新进行了改进，重新定义不等式约束的乘子为原乘子的正定函数，构造出一种直接对不等式约束进行处理的改进Lagrange乘子法。本文介绍的改进方法是对乘子法中另一个重要参数的更新方式进行改变，来研究另一个重要参数对算法迭代及收敛性的影响。

在交通信号控制方面，Meszaros等[12]基于延误和排放对交叉口的优化控制提出了建议；彭敏等[13]运用博弈论对交叉口的平均延误和停车延误进行优化；卫星等[14]推导出平均延误时间目标与绿灯配时之间的关系，在此模型的基础上采用自适应遗传算法进行优化。Lin等[15]利用综合宏观交通模型预测在不同操作条件下的交通流状态和排放，并应用于城市交通网络控制。胡亮等[16]将蜂群抑制算法应用到交通信号灯的控制中。

当前流行的智能算法，代码的编写较为复杂，例如遗传算法，需要对问题进行编码，找到最优解后有需要进行解码算法的搜索速度比较慢，要得要较精确的解需要较多的训练时间。Lagrange乘子法具有程序简单、迭代次数少、搜索范围大和收敛快等优点，并且该方法的耗时很少。根据动态车流实时配置信号灯状态是现在较为常用的方法，Lagrange乘子法具有较低的延误，可以对交通信号灯的状态进行实时配置。本文提出一种改进Lagrange乘子法，并应用到实际工程中去验证该种方法真实有效性。

本文综合考虑交叉口的机动车通行效率和环境效益两方面的优化，建立数学模型，通过权重系数的方式将这两个优化目标整合成单目标优化模型，权重系数设置为变量一同进行优化，从而可以达到交叉口性能的综合最优的目的。

1 改进Lagrange乘子法

Lagrange乘子法[17]是一种求解非线性约束问题的常用方法，该方法是通过构造拉格朗日函数和添加惩罚项来将有约束的问题转化为无约束问题进行求解，求解无约束问题的最小值。然而传统的Lagrange乘子法的罚参数的更新是固定的，更新方式为罚参数与一固定系数相乘。现将罚参数的固定系数改为与求得值偏离约束条件的大小有关的函数。新的算法有以下优点，惩罚参数的更新为一种自适应更新，当求得值偏离可行域越大时，增加罚参数的增加速度，该方法的全局搜索能力优与传统算法，罚参数的更新范围变大扩大了最小值的搜索范围，以及趋向最优值的速度。

1.1 一般约束问题

在交叉口的优化模型中，必然会存在各种等式及不等式约束，这样就构成了一般约束问题，一般约束问题的数学模型为

(1)

其中，hi(x)为等式约束，gi(x)为不等式约束。接下来需要运用改进的乘子法对一般问题的数学模型进行研究。

1.2 一般约束问题的乘子法

在构造增广拉格朗日函数时，添加辅助变量将不等式约束转化为等式约束，等式约束则通过与罚参数相乘来构造惩罚项，经过上述操作构造的增广拉格朗日函数为

(2)

更新乘子向量的迭代公式为

(μk+1)i=(μk)i-σhi(xk)
(λk+1)i=max{0,(λk)i-gi(xk)}

(3)

Lagrange乘子法中罚参数的更新方式为若βk/βk-1≥ϑ，更新罚参数，σk+1=ησk；否则，不更新罚参数，σk+1=σk。

1.3 Lagrange乘子法的改进

传统的方法罚参数的更新方式较为固定，并不能根据当前解偏离可行域的大小进行纠偏，可以加速算法的收敛速度，改进方法如下。

将罚参数更新公式改为

(4)

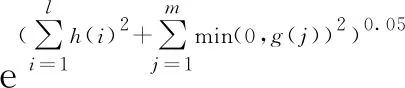
1.4 改进Lagrange乘子法的算法流程

Lagrange乘子法是Rockfellar在Powell和Hestenes提出的PH算法的基础上得到的，所以可以简称为PHR算法。将改进的罚参数修改后得到算法的流程如下：

步骤1 选取初值：

x0∈Rn,μ1∈Rl,λ1∈Rm,σ1>0,0<ε≪1,

ϑ∈(0,1),η>1,k=1。

步骤2 求解无约束子问题：

minψ(x,μk,λk,σk)

(5)

设初始点为xk-1,即可求得点xk。

步骤3 检验终止条件：

(6)

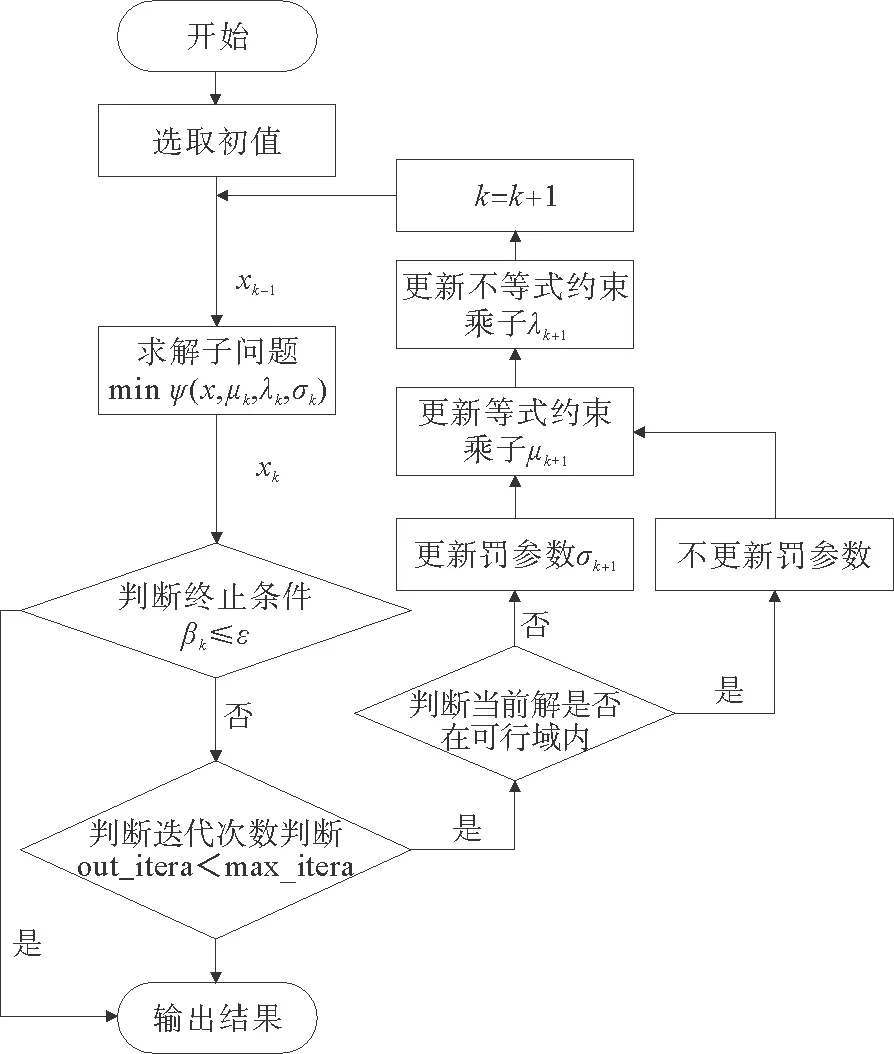
图1 改进罚参数的Lagrange乘子法算法流程

若βk≤ε，则停止迭代，输出xk为原问题的解；否则，转到下一步。

步骤4 更新罚参数σ：

(7)

步骤5 更新乘子向量：

(μk+1)i=(μk)i-σhi(xk)

(λk+1)i=max{0,(λk)i-gi(xk)}

(8)

步骤6 令k=k+1,转到步骤2。

流程图如图1所示。

2 信号控制优化模型

2.1 选取交通信号控制目标

评价交叉口的好坏有3个方面，即机动车效益、环境效益和行人效益。机动车效益包含了车辆通行能力、停车率、延误、排队长度等，环境效益包括了车辆通行时的燃油消耗及尾气排放，行人效益一般为行人等待时间。在此，我们综合考虑机动车效益和环境效益，既提高交叉口车辆通行效率又降低汽车尾气排放，从中选取最能代表每种效益的关键性能指标，本文选取了机动车延误和尾气排放来建立目标函数。

2.2 车辆延误与尾气排放模型

车辆延误是指机动车在信号控制的交叉口运行与在无信号控制及无其他车辆干扰下的行程时间的差值。可以选用Webster延误模型和美国道路通行能力手册(Highway Capacity Manual，HCM)延误模型，由于Webster延误模型经人们广泛地使用和验证，该模型适用于进口道饱和度较小时，饱和度范围一般在0～0.67内。而HCM延误模型适用于适应度较高的干道协调控制的延误计算。本文是在这两种模型的基础上来建立模型进行计算的，如式(9)[18]：

(9)

其中，dij为第i相位第j车道的车辆平均延误;c为交叉口周期长度;λi为第i相位绿信比;qij为第i相位第j车道的车流量;si为第i相位的饱和流量;yij为qij与si之比。

交叉口总延误为

(10)

车辆驶过交叉口时存在匀速、减速、怠速和加速行驶4种工况，每种工况的排放量不同，所以我们在分析交叉口的尾气排放量时将要分情况考虑。在计算交叉路口的排放量时，可分解为交叉口和路段的行车排放和因车辆延误造成的怠速排放，通过该种方法得到的排放模型[19]为

(11)

其中，eij为第i相位第j车道的排放量;e1为标准小汽车单位排放因子;Lij为第i相位第j车道路段长度;e2为标准小汽车单位怠速排放因子;dij为第i相位第j车道的车均延误。

交叉口一小时内车辆的总排放量为

(12)

2.3 建立优化目标模型

在建立优化模型时综合考虑交叉口的机动车效益和环境效益，其中车辆延误和尾气排放量是最能代表两个效益的指标，故选取车辆延误和尾气排放量作为优化目标。为达到一个综合的最优值，利用加权的形式放入到一个目标函数中，并考虑变量的范围，最终构建交叉口的优化模型为

(13)

其中，D、E分别为优化后的交叉口信号配时方案下的延误及排放量;D0、E0分别为原始配时方案下的交叉口延误及排放量;α与β为权重系数;cmin、cmax分别为交叉口最小、最大周期长度;gimin、gimax分别为交叉口第i相位最小、最大有效绿灯时间;L为一周期的总损失时间；n为交叉口内的相位数。

3 实例仿真

为验证该种方法的真实有效性，利用MATLAB R2015b将乘子法进行编程，并在CPU型号为Core i7-8565U，内存为8G的电脑上运行。选取青岛市黑龙江中路与九水东路交叉路口，该交叉口为双向三车道，道路状况良好无障碍物，根据道路实况以及Webster方法计算车道饱和度为1 500 pcu/h，对该路口在16:00-17:00的高峰期进行采集可知该路口处于非饱和状态，利用案例对本文提出的方法进行分析。

3.1 交叉口数据信息

该交叉口为四相位信号控制，信号相序以及原始配时的情况如图2所示，各路口车流量如表1所示。

模型中权重函数α、β也是两个变量，我们需要将交叉口通行能力和尾气排放量综合考虑。结果中，权重函数大的一方，优化的相对比例也大，实验证明交叉口通行能力和尾气排放量以如此的比值进行优化，就是最优结果。

一个周期交叉口的损失时间设置为10 s，选取CO(一氧化碳)作为尾气排放的目标，标准小汽车CO的排放因子为45 g/(pcu*km)，标准小汽车怠速排放因子为5 g/(pcu*h),最大、最小信号周期，最大最小有效绿灯时间的设置如表2所示。

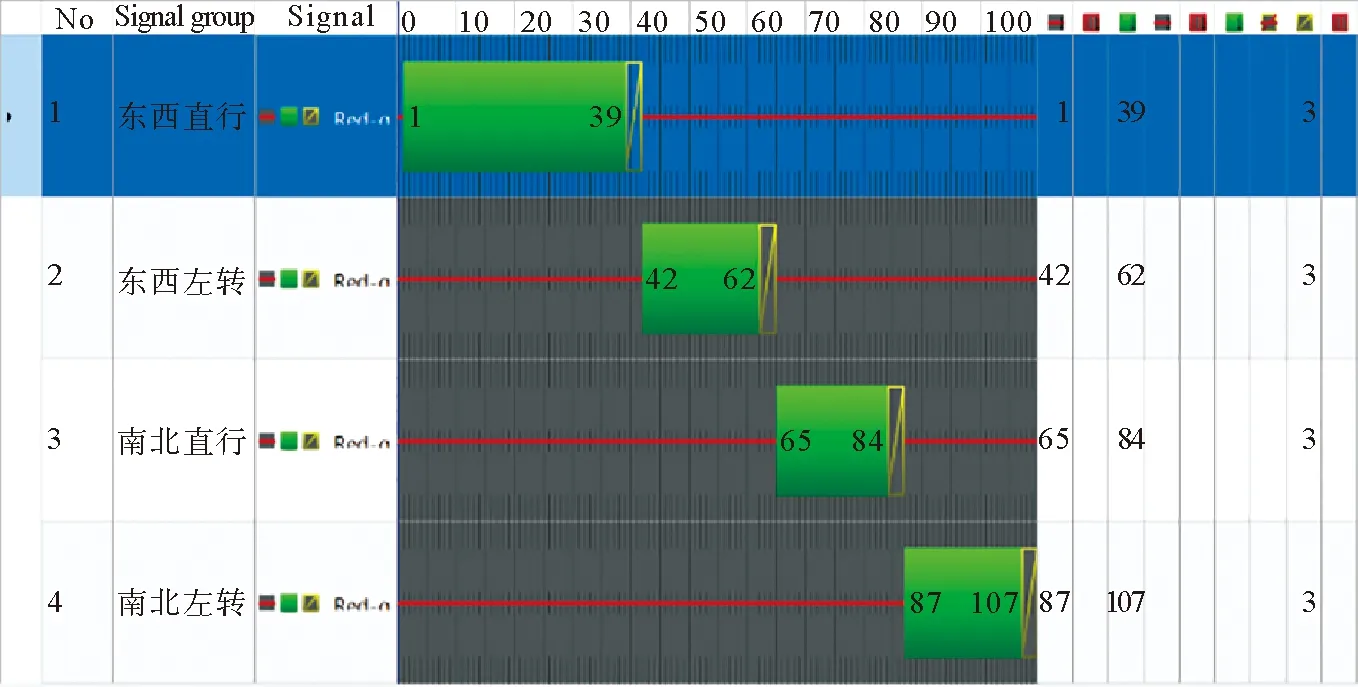
图2 信号相序及原始配时方案

表1 该交叉口16：00-17：00的小时车流量(pcu/h)

3.2 优化结果对比

为验证本文提出的改进Lagrange乘子法的优点，将本案例分别放到改进前后的Lagrange乘子法中分别进行优化，并记录每一代寻找到的最小值，运行得到两个方法的对比结果，如图3所示。

表2 交叉口信号配时参数

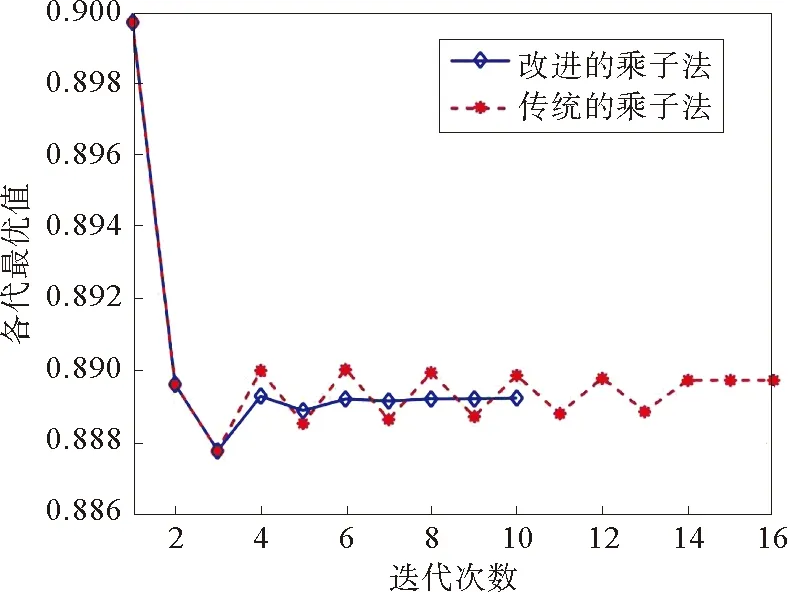
图3 改进前后乘子法求解配时问题的迭代过程

由图3可以看出，传统的Lagrange乘子法由于劣质的罚参数，导致数值的震荡剧烈无法迅速收敛，求得的解也无法快速趋向于可行域。而通过罚参数自适应更新的Lagrange乘子法，可以根据当前解偏离可行域的距离来适当加大罚参数，在7代左右就达到稳定值(传统乘子法14代以后才渐渐达到稳定)，并且求得的最小值也更优。可见该方法的收敛性和快速性优于传统的Lagrange乘子法。这里具体只研究改进Lagrange乘子法的优化配时等问题。

为更加直观地看出本文方法与智能算法在交通信号控制应用中的区别，将上述案例分别利用标准遗传算法和差分进化算法进行优化，得到的进化曲线如图4所示。

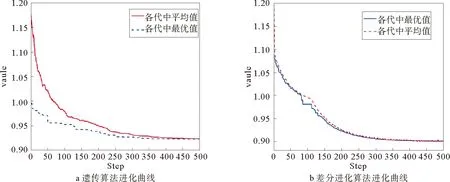
图4 两种智能算法的进化曲线

表3 算法耗时对比

Lagrange乘子法首先是找到最优值的大致范围，随后对当前解进行调整，使其位于可行域范围内；而智能算法是一个逐渐寻优的过程，算法迭代过程相对复杂。

从图3中可以看出，Lagrange乘子法在迭代10代左右就可以准确地找到最优值，而本文介绍的遗传算法和差分进化算法需要200～300次左右才能逐渐找到最优值。

在编写代码时记录算法的耗时，将几种算法的耗时进行对比，如表3所示。

由图3和表3可知，经本文方法改进后Lagrange乘子法的耗时更少，收敛更快，精度更高；由于智能算法的计算量巨大，迭代复杂，算法耗时相对较高。遗传算法和差分进化的最优值分别为0.910 8和0.899 6，差分进化算法的优化结果优于遗传算法。接下来将改进Lagrange乘子法与差分进化算法进行对比分析，结果如表4所示。

表4 信号配时优化结果对比

经过结果的对比可知，乘子法优化的配时使延误降低了19.89%，排放降低了2.379%；差分进化算法优化的配时使延误降低了18.9%，排放降低了1.723%。上述优化结果使延误大幅度降低，但排放却优化很少，主要原因是在权重系数的分配过程中，将优化的比例大部分分给了延误，该种配时适用于拥堵严重的路口以及继续降低延误的情况。而当排放污染严重，此时就需要大比例优化排放。为解决这种问题，不再将权重系数看作变量，而是根据需要将β值设置得更高。权重系数的方法可以适用于各种不同的情况，适用范围广泛，不再局限于单个交叉口性能优化。

3.3 VISSIM仿真

根据青岛市黑龙江中路与九水东路交叉路口的实际情况搭建VISSIM仿真模型，如图5所示。

为验证本文方法的真实有效性，将优化前后的配时利用微观交通仿真软件VISSIM进行进一步的验证，在仿真软件中选择输出交叉口的车辆延误及CO的尾气排放量。仿真周期设置为1 h，每60 s对该交叉口的数据进行采集，将输出结果绘制成折线图，如图6所示。

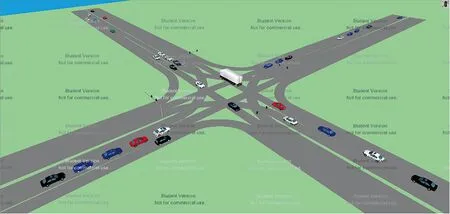
图5 青岛市黑龙江中路与九水东路VISSIM仿真模型

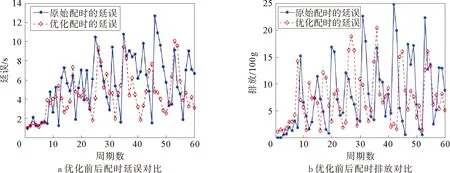
图6 优化前后配时于VISSIM仿真结果

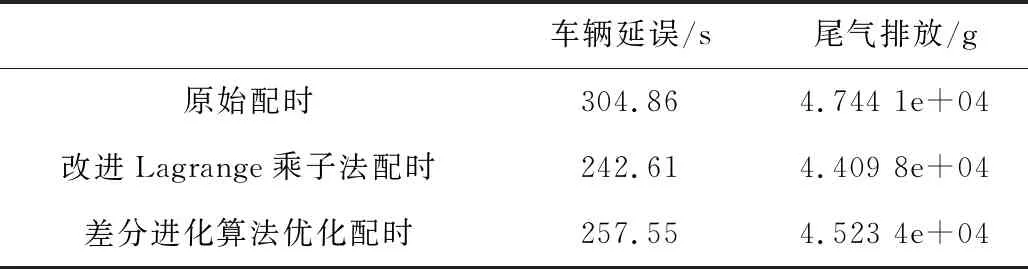
表5 在VISSIM中各种配时的仿真结果

将各种配时分别输入到VISSIM中进行仿真对比，得到的车辆延误及CO尾气排放量的对比如表5所示。

综合VISSIM仿真的延误与排放的优化结果，本文的方法对于优化交叉口延误以及排放是十分有效的，具有较强的全局搜索能力，相对于智能算法也具有一定的优势。整体来看，本文提出的信号优化配时的方法以及建立的多目标优化模型都是有效的。

4 结论

为提高城市交叉口的通行效率，减少机动车尾气排放，本文从综合考虑机动车通行效率与环境效益的角度出发，建立以交叉口处的机动车延误及尾气排放量为综合优化指标的目标优化模型，改进传统Lagrange乘子法收敛慢、精度不高等问题，并将该方法应用到交通信号控制中。从VISSIM仿真结果得出，改进Lagrange乘子法优化配时令车辆延误降低20.42%，一氧化碳尾气排放量降低7.046%。与差分进化算法得到的配时，在延误方面降低了15.52%，排放方面降低了4.65%，本文方法在延误方面比差分进化算法减少了6.16%，排放方面降低了2.58%。本文方法寻找的最优值略优于智能算法的最优值。

在面临多种情况时，可对优化目标添加不同的权重，将优化的重点放到我们需要优化的目标中。本文的方法针对于单交叉路口，将两个目标函数合并成一个，从而达到了整体上的优化，克服了单目标优化不能综合考虑交叉口性能的弊端。本文仅研究单交叉路口，后续可以应用到路口存在相关联的区域交通信号优化控制中。