Wasserstein距离驱动的低维流形图像修复
2021-12-25何瑞强王立志王彩云
何瑞强,王立志,王彩云
(忻州师范学院 数学系,山西 忻州 034000)
0 引言
图像修复是图像处理和计算机视觉领域研究活跃的课题。图像修复的目的是从退化图像f中恢复潜在的干净图像u。一个广泛使用的观测模型是f=Au+ε[1-5],其中,A是退化算子,ε是高斯白噪声。现有的图像修复方法可以分为基于学习的方法[4-5]和基于模型的方法[6-12]。通过将图像近似为分片光滑函数,DongBin等人给出一种用于图像修复的边缘驱动小波框架模型(Edge Driven Wavelet Frame,EDWF)[13]。利用自然图像块流形的低维结构[14-15],一种用于图像修复的低维流形模型(Low Dimensional Manifold Mode,LDMM)[16]被提出。在LDMM里,点积分方法所产生的线性系统并不对称,导致迭代次数很多。为了克服LDMM的局限性,Shi等人利用加权非局部Laplace代替点积分方法,提出了低维流形的推广模型(Generalization of the LDMM,G-LDMM)[17]。通过图像块DCT系数似然的最大化,同时兼顾重叠块的一致性,一种图像修复方法PACO-DCT[18]被呈现。这些方法在修复图像时要付出较大的计算代价,且修复结果含有细节损失或划痕残余。
作为高斯分布的一种离散逼近,高斯噪声直方图[19-20]具有构建容易且稳定的特性;同时Wasserstein距离可以度量两个概率分布的统计差异。基于此,本文利用Wasserstein距离[21]将被估计噪声直方图和参照噪声直方图的统计差异最小化,进而提出一种Wasserstein距离驱动的低维流形模型。不同于以往Wasserstein距离在彩色迁移、图像分割中的作用,本文模型将Wasserstein距离噪声估计与低维流形图像约束相统一,用于含噪图像修复。本文创新点在于:通过Wasserstein距离将噪声直方图约束嵌入图像修复整体优化模型,且直方图匹配和加权非局部Laplace交替迭代算法具有修复效果好、实现效率高的特点。
1 Wasserstein距离和低维流形
本节简单介绍Wasserstein距离和低维流形相关知识。
1.1 Wasserstein距离
源于最优传输理论的Wasserstein距离是两个概率分布或者直方图差异性的一种统计度量。对于定义在实数域上的两个分布p和q,它们之间的Wasserstein距离为以下Monge问题[21]的变分解:
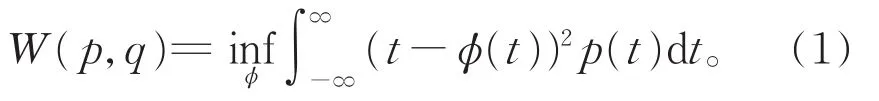
上述问题的下确界指对所有确定的实函数φ:R→R而言,变量t和φ(t)分别服从分布p和q。
事实上,(1)式是一个期望值,于是分布p和q的Wasserstein距离也可以表示为:

若将t=(t1,t2,…,tn)T视为源自概率分布p的n个独立样本,直方图hq看作另一个分布q的离散逼近。这时,Wasserstein距离的离散定义为:

其 中,φ将ti映射为ξi=φ(ti),采样ξ=(ξ1,ξ2,…,ξn)T符合直方图hq。(3)的闭式解为
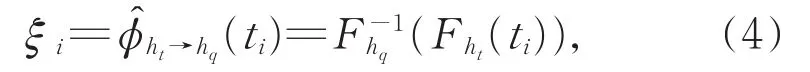
其中,Fht和分别是累积分布函数和百分位函数,且分别源于直方图ht和hq。若t是一幅图像,则表示直方图匹配运算[22]。对于给定输入图像t=(t1,t2,…,tn)T,可使输出图像ξ=(ξ1,ξ2,…,ξn)T匹配已知直方图hq。
1.2 低维流形
考虑一个m×n大小的图像u∈Rm×n。对于任意像素x∈={1,2,…,m}×{1,2,…,n},定义(pu)(x)为图像u的以x为左上角像素的矩形像素块,其大小为s1×s2。P(u)是图像u的所有这些块构成的集合,
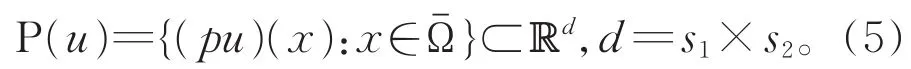
图像u的块集合P(u)给出Rd中的一个点云。这个点云往往能够逼近嵌套在Rd中的一个光滑流形。这种潜在的光滑流形称为块流形,记作M(u)。基于许多自然图像块流形常常有低维结构这一事实[15-16],osher等人设计了下面的低维流形模型[16]:

其中,dim(M)是图像块流形的维数,f为退化图像。利用以上模型,osher等人给出了较好的图像恢复效果。
2 提出的图像修复模型
Wasserstein距离被认为是度量两个概率分布或直方图统计距离的强大工具[21]。可以充分利用Wasserstein距离这一优势,来使被估计噪声直方图尽可能逼近参照噪声直方图,进而提升噪声估计的准确性。另一方面,许多自然图像具有较低的块流形维数,这一结论在近年来的许多研究中已得到验证[16-17]。因此,一个自然的理念就是将图像块流形维数作为数据项来修复图像。用于噪声估计的Wasserstein距离和用于图像约束的低维流形是相互补充的。
基于以上分析,我们提出下列Wasserstein距离驱动的低维流形图像修复模型:
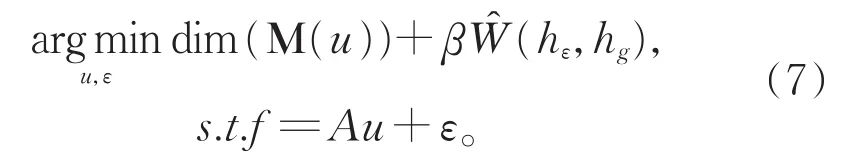
在上述优化模型中,dim(M(u))表示被恢复的干净图像u的块流形维数,(hε,hg)是估计噪声ε的直方图hε和真正的高斯噪声直方图hg之间的Wasserstein距离。可以看出,提出的模型(7)是Wasserstein距离噪声估计和低维流形图像正则的统一体。接下来,针对该模型做一些具体分析。
2.1 流形维数和Wasserstein距离互补性分析
在提出的图像修复模型中,原始图像块流形维数 dim(M(u))和噪声 Wasserstein正则项(hε,hg)是相互补充的,而不是孤立的、无关的。接下来,从两方面具体分析。首先,我们取1×3大小的图像块在R3中直观地展示原始图像“house”和σ=100的高斯噪声块流形维数,结果如图1所示。显然,原始干净图像块流形是一维的,而高斯噪声块流形是三维的,也就是说,原始图像块流形维数dim(M(u))是小于噪声块流形维数dim(M(ε))的。
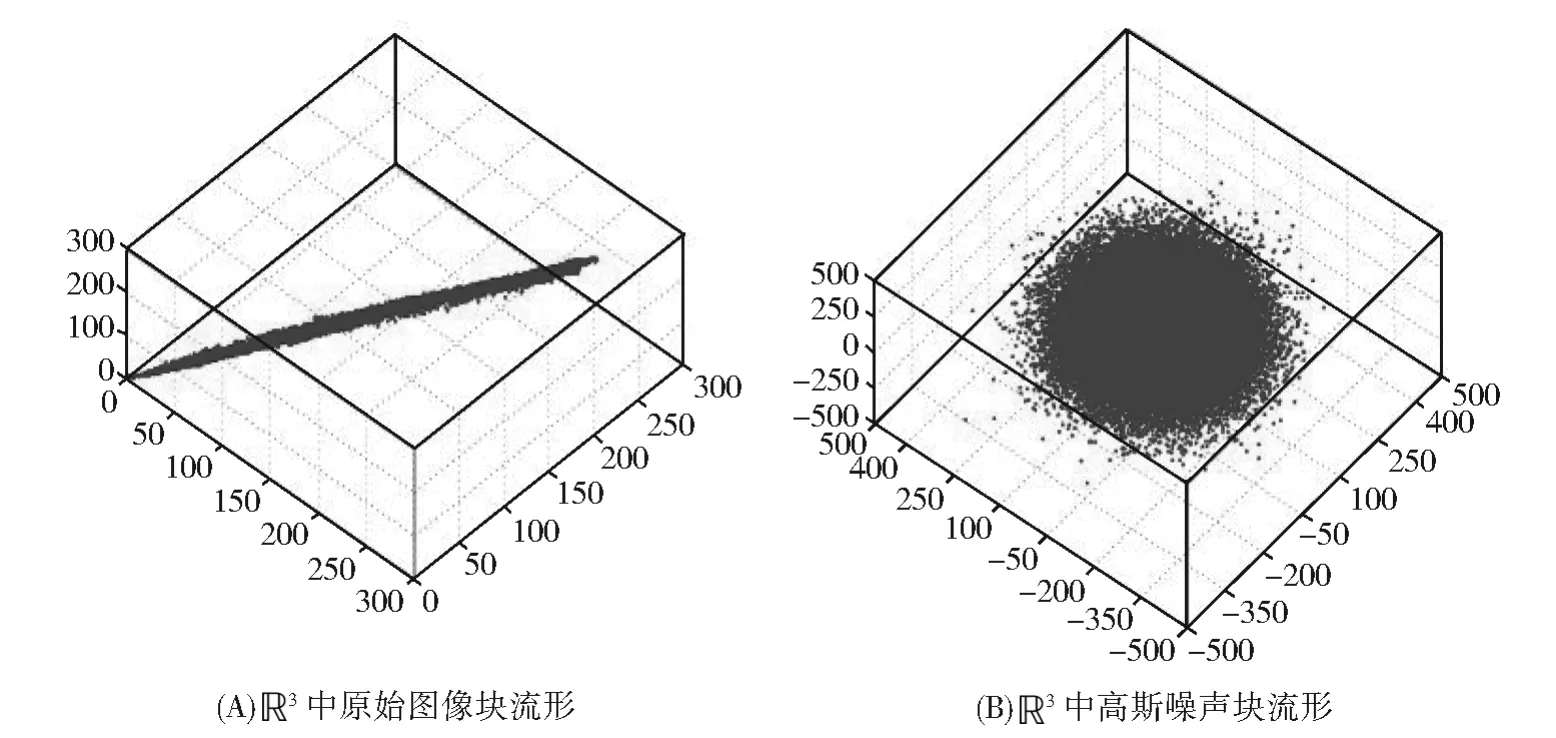
图1 原始图像和高斯噪声块流形维数示意图Fig.1 Dimensional schematic diagrams of original image and Gaussian noise block manifold
另一方面,对于给定的参照高斯噪声直方图hg(见2.2节分析),分别计算原始图像直方图hu和hg的Wasserstein距离(hu,hg)、估计的噪声直方图hε和hg之间的Wasserstein 距离(hε,hg),结果如表1所示。可以发现,(hu,hg)大约是(hε,hg)的 32倍,也就是,(hε,hg)是远小于(hu,hg)的。结合dim(M(u))是小于 dim(M(ε))的,可以说明,提出模型中的dim(M(u))和(hε,hg)是相互补充的。可以利用二者的最小化来得出期待的修复结果图像。

表1 流形维数和Wasserstein距离互补性数据表Table 1 Complementarity data for manifold dimension and Wasserstein distance
2.2 参照高斯噪声直方图稳定性分析
在提出的图像修复模型(7)里,参照高斯噪声直方图hg很重要,因为它决定着噪声估计的准确性。为了分析hg的稳定性,随机生成十幅高斯噪声直方图,如图2所示。这里的高斯噪声都是均值为0,方差为25的随机噪声。实验数据显示,上述十幅直方图均值和方差的平均值分别为-0.003 5和25.002 0。同时,对应上述十幅噪声直方图标准差的方差为2.6966×10-4。由此可见,提出模型(7)里的参照高斯噪声直方图hg是稳定的。
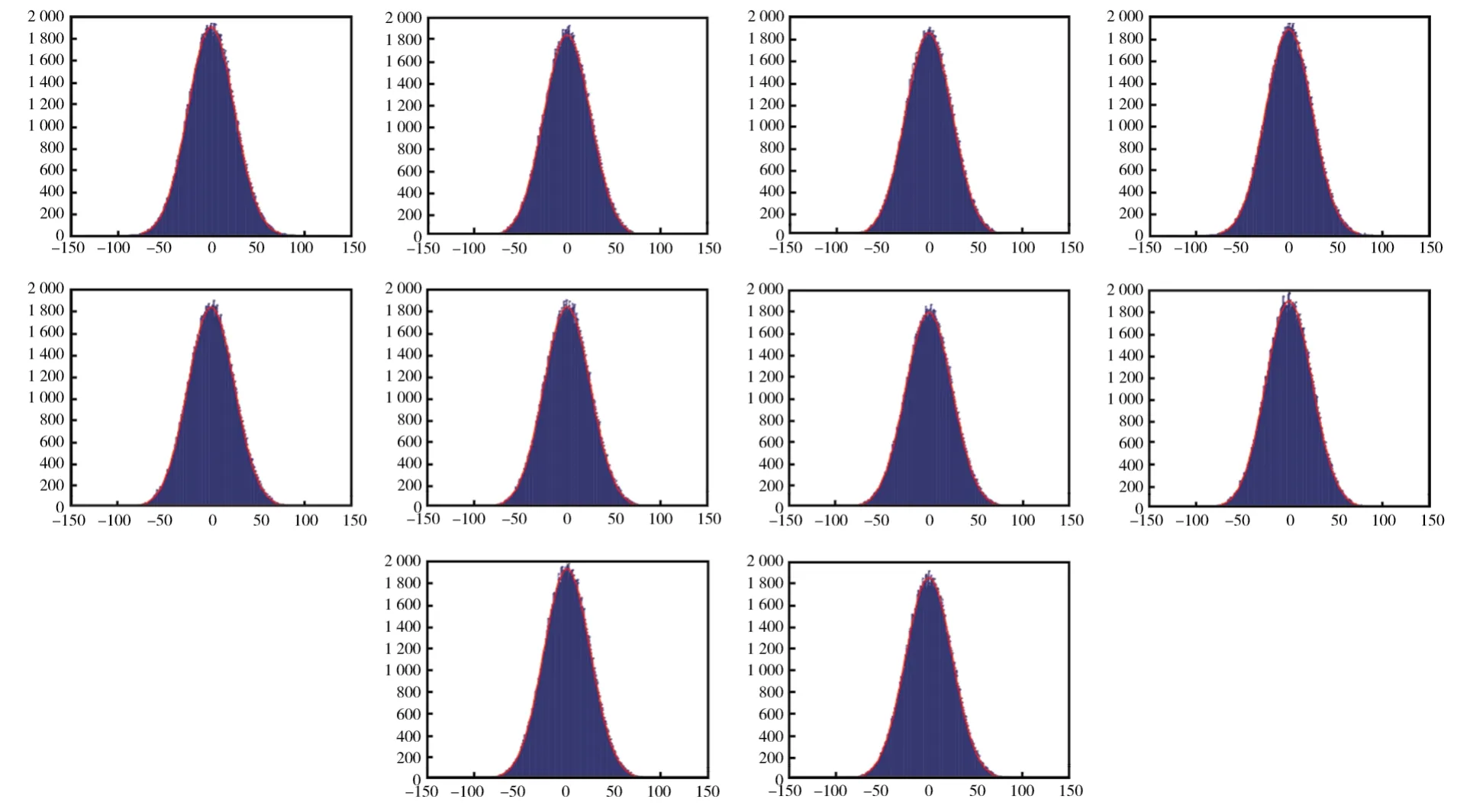
图2 10个随机生成的高斯噪声直方图Fig.2 Ten randomly generated Gaussian noise histograms
2.3 Wasserstein距离的作用分析
为了验证提出模型(7)中Wasserstein距离的作用,利用所提方法,取β=0(不含Wasserstein距离项)和β≠0(含有Wasserstein距离项)进行噪声估计实验,结果如图3所示。蓝色表示真正的高斯噪声概率密度曲线,绿色和红色分别表示本文方法在β=0和β≠0时所估计噪声的概率密度曲线。显然,β≠0时的概率密度曲线更接近真正的高斯噪声密度曲线,这就暗示,Wasserstein距离的使用可以提升噪声估计的准确性。
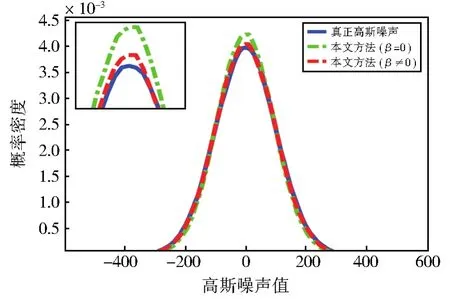
图3 概率密度曲线比较图Fig.3 Comparison of probability density curves
3 图像修复模型的求解
在本节中,先呈现提出优化模型的求解过程,然后设计对应的图像修复算法。
3.1 求解过程
为了求解提出的图像修复模型(7),首先引入一个辅助变量ξ,于是问题(7)可分裂为

上述约束优化问题(8)可以通过分别固定ε、u(ε、u被同时固定)和ξ来求解。
当固定ε、u时,最小化问题(8)可以转化为

基于Wasserstein距离理论[21],上述问题中最优的ξ可以通过下列直方图匹配运算[22]来获得,
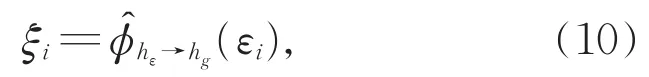
其中,i代表第i个元素。
另一方面,当ξ被固定时,最优化问题(8)可以降为
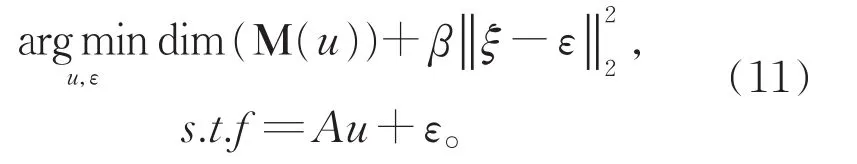
显然,(11)可以转化为下面的无约束优化问题,

为了符号简化,设z=f-ξ,(12)即为以下表达式
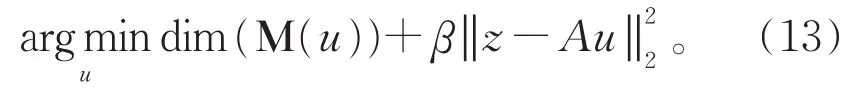
在图像修复的优化问题(7)里,对应的算子A可以表示为
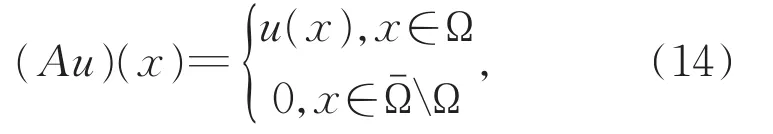
只要(13)式中的最小点u得到求解,噪声估计的进一步更新可获得

综上所述,求解图像修复模型(8)的主要步骤为交替地求解直方图匹配运算(10)和优化问题(13)。接下来,重点求解优化问题(13)。首先做一些分析,注意到(13)是下面问题,
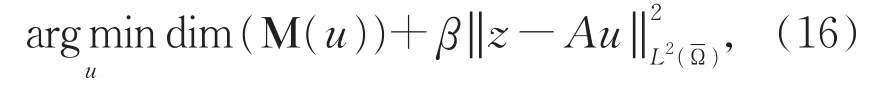
可以发现,上式(16)可以转化为

事实上,下面的理由可以解释(16)和(17)是同一个问题。具体地,(16)可以分为两项

考虑到(14)式中,当x∈Ω时,(Au)(x)=0,上述(18)式即为

这就是前面的(17)式。
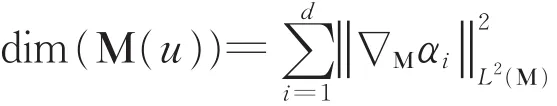

利用加权非局部Laplace思想,我们可以获得下面的离散优化问题:

其中,Ωi={x∈:(piu)(x)被采样 }是坐标函数αi的采样集。
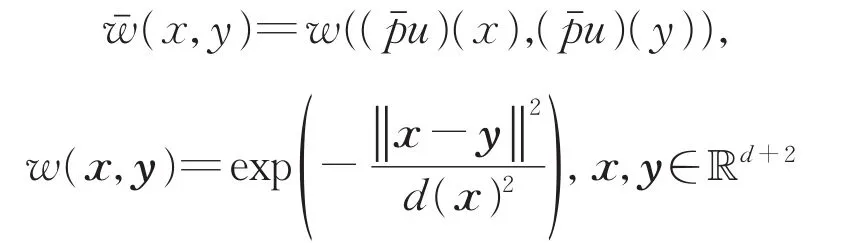
是两个半局部块,d(x)是半局部块x和它的第20个最近邻的距离。
使用标准的变分方法,可以得到对应(21)式的Euler-Lagrange方程,见式(22)。式(22)中的是pi的伴随算子,参数η取。
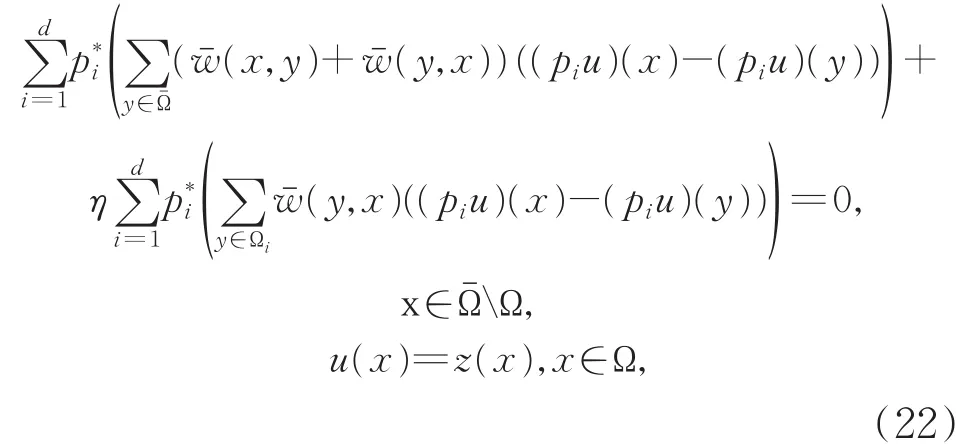
3.2 算法设计
基于模型的求解过程,Wasserstein距离驱动的低维流形图像修复方法可以总结为算法1。


4 数值实验
为了验证图像修复算法的效果,本节展示对应的数值实验,包括参数设置和实验结果。
4.1 参数设置
数值实验中,使用灰度级为0到255的512×512大小的图像作为测试图。图像修复算法中的半局部块设置为
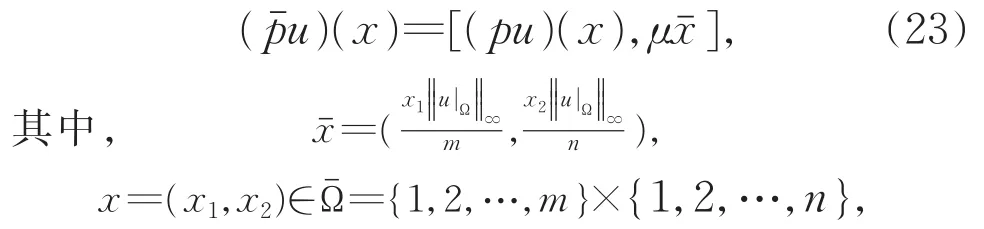
m,n是原图像尺寸,块大小为8×8。半局部权μ随迭代次数k变化如下:
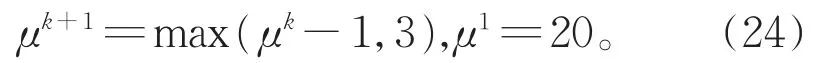
基于实践经验,在直方图匹配运算中,初始噪声值设为Magic矩阵,即每行每列每个对角线元素和值一样的矩阵,该矩阵大小m×n。在算法1的实施过程中,半局部块集合和图像交替更新18次,即M=18。直方图匹配运算和图像交替更新两次,即J=2。关于对比实验,我们采用了相关参考文献中建议的参数设置。
实验中,采用峰值信噪比(PSNR)进行模型的客观评价。PSNR定义可表述为

其中,均方误差MSE定义为
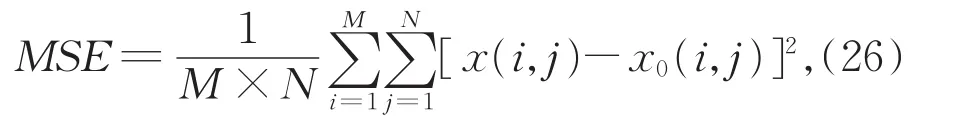
这里,M×N是图像的大小,x0和x分别表示原始图像和去噪图像。PSNR能够很好地对去噪图像和原始图像差异性进行比较。PSNR越大,说明所恢复图像失真程度越低,去噪效果越好。
实验硬件平台为双核CPU(2.10 GHz和2.10 GHz),64.0 GB RAM,软件环境为 Windows 10.0操作系统,编程环境为Matlab R2017b。
4.2 实验结果
为了测试图像修复算法的有效性,将本文提出的方法和近年来流行的图像修复方法EDWF[13]、LDMM[16]、G-LDMM[17]、PACO-DCT[18]进行比较。我们将所提方法应用到两类图像上:一类图像含有文本和噪声,另一类图像含有划痕、文本和噪声。
4.2.1 退化图像含有文本和噪声
在表2和图4中,分别显示了四种图像修复方法的数值和视觉实验结果。实验中退化图像包含文本和σ=3的高斯噪声。从表2可以发现,提出方法的平均 PSNR 要比 EDWF[13],LDMM[16],GLDMM[17],PACO-DCT[18]分别高出 1.85 dB,1.59 dB、0.99 dB和0.60 dB。在平均PSNR方面,本文方法比现有表现极好的PACO-DCT[18]提高了1.97%。图4显示了部分修复结果图。可以看出,提出的方法能够恢复令人满意的修复结果。另外,在图5中,呈现了图像“Plane”的局部放大效果图。显然,EDWF[13],LDMM[16],G-LDMM[17]、PACODCT[18]的结果图在机尾黑色区域左上角或右上角有损失,而本文方法却能恢复较完整的区域。可见,与比较方法相比,本文的修复效果有明显优势。

图4 含有文本和噪声图像的修复结果比较Fig.4 Inpainting result comparison of images containing text and noise

图5 修复图像的局部放大图比较Fig.5 Local magnification comparison of inpainted images
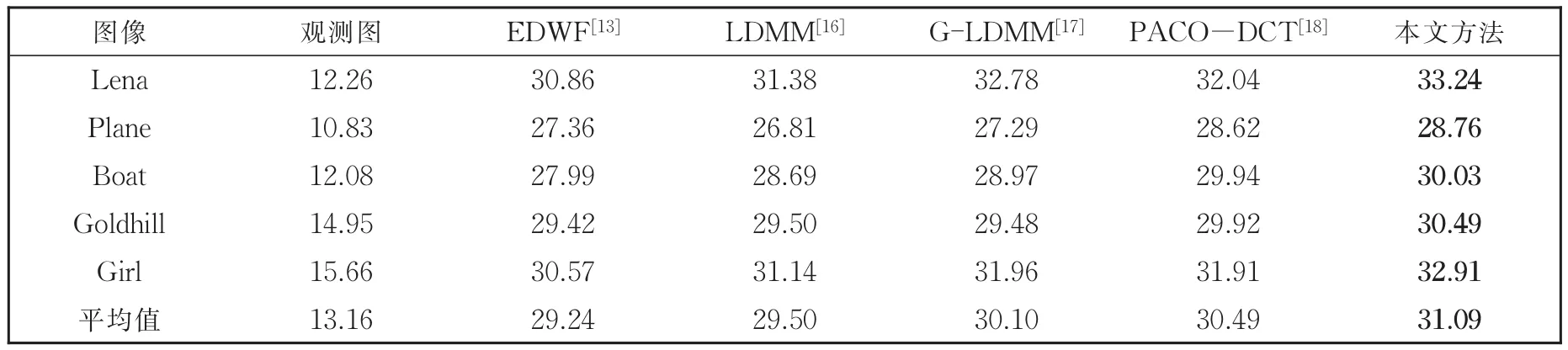
表2 含有文本和噪声的图像修复PSNR结果Table 2 Inpainting PSNR results of images containing text and noise
4.2.2 退化图像含有划痕、文本和噪声
表3和图6分别展示了四种方法的图像修复数值和视觉结果。该部分退化图像含有划痕、文本和σ=3的高斯噪声。由表3可以发现,提出的修复方法平均PSNR明显优于近年来一些方法EDWF[13]、LDMM[16]、G-LDMM[17]和 PACO-DCT[18]。本 文方法比现有表现极好的PACO-DCT在平均PSNR方面提高了0.94%。图6展示了含有划痕、文本和噪声的图像修复视觉比较。我们以图像“Plane”修复结果为例分析。EDWF修复图像在机尾“F-16”处存在划痕残余,LDMM机头上方黑色横线划痕未被修复,G-LDMM和PACO-DCT机身字母“U”变模糊了,而提出的方法在上述几处修复效果比较好。由此可见,本文方法能较好地去除划痕残余,同时保留比较清晰的原图细节信息。提出方法在图像修复方面能够取得较好效果,这要归功于Was-serstein距离噪声直方图逼近和低维流形图像约束的组合作用。

图6 含有划痕、文本和噪声的图像修复结果比较Fig.6 Inpainting result comparison of images containing scratches,text and noise
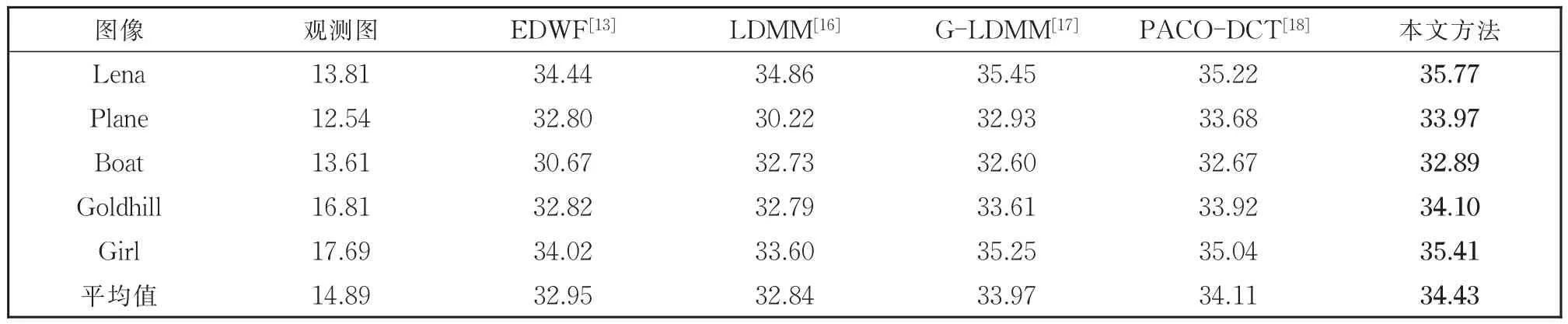
表3 含有划痕、文本和噪声的图像修复PSNR结果Table 3 Inpainting PSNR results of images containing scratch,text and noise
最后,通过表4呈现了四种修复方法的运行时间。由表可见,在实现效率方面,本文方法比现有表现极好的PACO-DCT用时缩短了10.6%。这就说明,所提方法在提高图像修复效果的同时,也提高了代码执行的效率。具体地分析,EDWF通过将图像近似为分片光滑函数,引入一种边缘驱动的小波框架模型,该方法对平滑和奇异的图像区域、边缘施加不同强度的正则化要耗费较长的运算时间;LDMM和G-LDMM在利用点积分方法和加权非局部Laplace处理优化约束方面,具有较高的计算代价,且算法迭代次数多,这些导致了运行时间较长。相比较而言,本文提出的Wasserstein距离驱动的低维流形图像修复算法(算法1)在内循环中半局部块和图像交替更新18次,而在外循环中直方图匹配和图像更新只交替实施2次,即可实现较好的图像修复效果。因此,提出的方法利用较少的迭代次数实现了图像修复效果的提升。该方法在实现效率上具有明显优势。

表4 四种图像修复方法运行时间比较Table 4 Running time of four image inpainting methods
5 结论
本文提出一种新的Wasserstein距离驱动的低维流形模型,用于处理含噪图像修复问题。不同于大多数图像修复模型,该模型将噪声估计和图像先验约束相结合。用于噪声估计的Wasserstein距离和用于图像约束的低维流形,在功能上是相互补充,而非孤立的。在Wasserstein距离的驱动下,被估计噪声的直方图尽可能地靠近真正的高斯噪声直方图,从而提升噪声估计的精准度。同时,充分利用图像块流形的低维结构来修复图像。模型求解过程中,加权非局部Laplace和半局部块扮演着重要角色。所提方法不仅可以获得主、客观方面较好的评价效果,而且具有较高的实现效率。
本文所提出的Wasserstein距离驱动的低维流形模型为图像恢复问题提供了框架,即图像约束和余量正则可以共同作用来恢复期待的图像。基于图像修复的研究思路,未来研究工作的一个方向是将该框架用于图像去模糊、超分辨任务,以进一步提升图像恢复效果。
