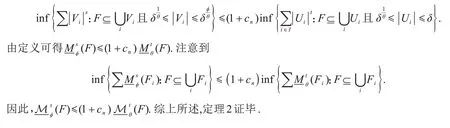修正的中间测度和维数
2022-12-06赖健强宋子婷
赖健强 ,宋子婷
(1.广州大学数学与信息科学学院,广东广州 510000;2.闽南师范大学数学与统计学院,福建漳州 363000)
Hausdorff[1]维数在分形几何及其他学科,如物理、地理学科中扮演着越来越重要的角色.盒维数是另外一种更容易计算的维数.这些维数可用来刻画物体占据空间的能力,具有广泛的应用.2019年,Falconer等[2]引入了上、下中间维数的概念,它是在Hausdorff 维数和盒维数之间通过限制Hausdorff 维数定义中允许的覆盖来实现的.中间维数介于Hausdorff 维数和盒维数之间,近来取得许多有意思的结果,见文献[3-10].但上、下中间维数没有可数稳定性,大大限制了其应用范围.使用修正的上,下中间(s维)测度来分别诱导修正的上、下中间维数,并讨论了这些测度和维数的一些性质.
1 预备知识
设0≤θ≤1,δ>0,F⊆Rn.若F⊆,对任意i,都有,则称为F的一个(θ,δ)-覆盖.Falconer等[2]引入的上、下中间维数的定义如下:

设F是Rn的有界子集,0≤θ≤1,s为一非负数,对任意δ>0定义:
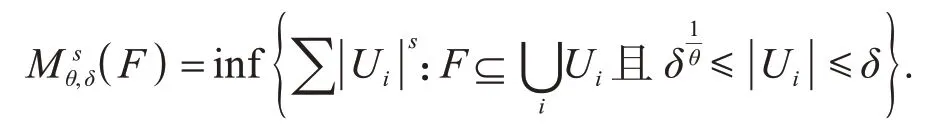
集合F的修正的上、下中间测度分别定义为
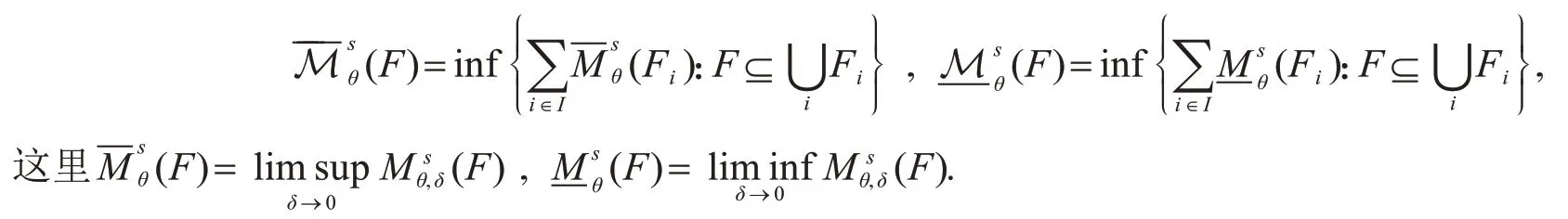
可以用通常的方法定义修正的上、下中间维数:

2 主要结果
定理1是度量外测度.不是度量外测度.
集合在HÖlder映射下像集的修正的上、下中间测度有如下的估计.
命题1令F⊆Rn,f:F→Rm是满足α阶HÖlder条件的映射,则对每一个s有

以下关于修正的上、下中间维数的变换性质,可以从命题2中立即得到.
推论1令F⊆Rn,f:F→Rm是满足α阶HÖlder条件的映射,则对每一个s有

定理2设F是Rn的有界集,0<θ<ϕ≤1和t<,令cn=,则

同样修正的上、下中间维数关于θ∈(0,1]的连续性质,可以从定理2中立即得到.
推论2设F是Rn的有界集,并且令 0<θ<ϕ≤1和t<,则有
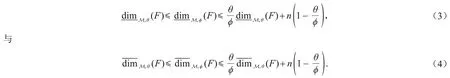
3 主要结果的证明
定理1的证明 因为是由方法I[3]得到,故为外测度.下证为度量外测度.

对F的所有(θ,δ)-覆盖取下确界,得到
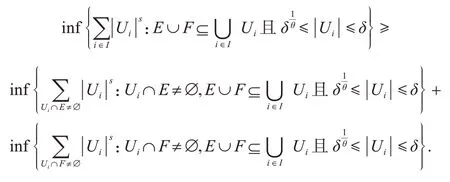
因此
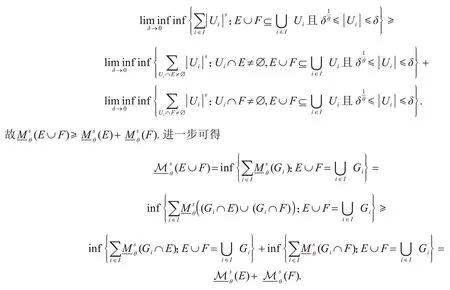
综上所述,定理1证毕.