多重卷积流形上的梯度近Ricci孤立子
2022-05-30沈东
沈 东
(西北师范大学 数学与统计学院, 兰州 730070)
1 引言及主要结果
若Riemann流形(Mn,g)上存在两个实值光滑函数ψ和ρ, 满足方程
Ric+Hess(ψ)=ρg,
(1)
则称(Mn,g)为梯度近Ricci孤立子[1], 记为(Mn,g,ψ,ρ), 并称ψ为势函数, 其中Hess(ψ)=2ψ表示势函数ψ的Hesse算子,Ric为Mn的Ricci曲率张量.
梯度近Ricci孤立子是Ricci-Bourguignon流的自相似解[2], 也是Einstein流形的推广形式(包括梯度Ricci孤立子, 梯度近Ricci孤立子, 梯度Yamabe孤立子), 它与卷积流形[3]有紧密联系. Kim等[4]给出了卷积形式的Einstein流形. 而多重卷积流形是卷积流形的自然推广.
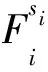

(2)
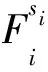
多重卷积流形在微分几何和理论物理的广义相对论中均有重要意义.例如当m=2时, 若在M=××S2上赋予如下度量g:
则(M,g)即为Reissner-Nordström时空(Schwarzschild黑洞的特殊情形), 其中m表示质量,q表示电荷; 若在M=×Sk×F上赋予如下度量:
g=-dt2+cosh2tgSk+gF,
则(M,g)即为de Sitter时空, 其中(F,gF)为Riemann流形; 当m=1时, 若在M=×Sk上赋予度量g=-dt2+cosh2tgSk, 则得到的Riemann流形(M,g)即为广义Robertson-Walker时空[6]. 此外, 通过求解卷积函数的显式解, 可得相应多重卷积时空是Einstein时空. 例如, 文献[7]给出了卷积函数的一些特殊形式, 使得对应的广义Robertson-Walker时空是常数量曲率空间; 文献[8]得到了卷积函数的特解, 使得广义Robertson-Walker时空是Einstein流形, 且其纤维也是Einstein流形.
在微分几何中, 研究多重卷积流形上的Einstein度量及其推广形式对于构造具有某种曲率性质的Riemann度量具有重要意义, 目前已取得了许多成果. 例如: 文献[4]得到了卷积流形是Einstein流形的充要条件; 文献[9-10]将Einstein流形推广到梯度Ricci孤立子. 其中文献[9]构造了一个稳定Ricci孤立子, 其形式是卷积流形(0,+∞)×fSm,m>1, 卷积函数f是一条射线; 文献[10]证明了卷积流形上的梯度收缩Ricci孤立子是紧致Riemann流形的必要条件是其基流形是紧致的, 且纤维流形的维数至少为2, 并得到了卷积流形是梯度Ricci孤立子的充要条件; 文献[11]将卷积流形推广到多重卷积流形, 得到了多重卷积流形是梯度Ricci孤立子的充要条件.
基于此, 本文讨论多重卷积流形上的梯度近Ricci孤立子, 得到如下结果.




2)λ≤0, 且λ(p)≤λ(q), 其中p,q分别是函数b的最大值点和最小值点.
则Mn是多重Riemann积梯度Ricci孤立子.
2 预备知识
设(Mn=Br×b1F1×b2F2×…×bmFm,g)是n维多重卷积流形.若Mn上具有梯度近Ricci孤立子(Mn,g,ψ,ρ)的结构(即满足式(1)), 则称(Mn,g,ψ,ρ)为多重卷积梯度近Ricci孤立子.特别地, 若bi(1≤i≤m)为常数, 则称(Mn,g,ψ,ρ)为多重Riemann积梯度近Ricci孤立子.

设(Mn,g)是n维多重卷积流形,T是Mn上的(0,2)型张量,ψ是Mn上的光滑函数, 则由散度和梯度的定义可得:
1) div(ψT)=ψdiv(T)+T(ψ,·);
3) div(Hess(ψ))=Ric(ψ,·)+d(Δψ);
5) div(ψg)=div(ψ)=dψ.
二阶椭圆算子强最大值原理的定义可参见文献[13-14].设B是r维Riemann流形,u,φ,c是B上的3个光滑函数, 且c≥0.在B上定义一个二阶椭圆算子
ε(·)∶=Δ(·)-φ(·)+c(b(·)).

为方便, 本文约定D,,Ric,Δ分别表示Mn上的Levi-Civita联络、 梯度、 Ricci张量、 Laplace算子;BD,FiD,B,Fi,ΔB,ΔFi,RicB,RicFi分别表示Br,上的Levi-Civita联络、 梯度、 Laplace算子、 Ricci张量;分别表示Ricci张量和Hesse算子的Br,上提升;Hess(ψ),Hess(φ)分别表示Mn和Br上光滑函数ψ∈C∞(M),φ∈C∞(B)的Hesse算子, 1≤i≤m.
引理1[15]设(Mn,g)是多重卷积流形, 若X,Y∈L(B)且V∈L(Fi),W∈L(Fj), 则:
1)DXY是BDXY的B上提升;
引理2[15]设(Mn,g)是多重卷积流形, 且φ:B→(0,+∞)是B上的光滑函数, 则:
引理3[15]设(Mn,g)是多重卷积流形.若X,Y∈L(B)且V∈L(Fi),W∈L(Fj), 则:
2)Ric(X,V)=0;
3) 当i≠j时,Ric(V,W)=0;
4) 当i=j时,

3 多重卷积流形上梯度近Ricci孤立子的性质

其中c为常数.


(3)
由引理4, 式(3)可转化为
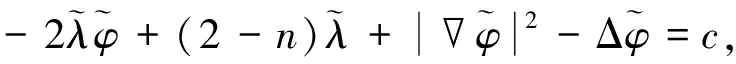
(4)
其中c为常数.再由引理2, 式(4)可转化为
证毕.
性质1中若bi=b(1≤i≤m), 其中bi是B上的光滑函数, 则可得下列推论.

其中c为常数.
性质2设(Br,gB)是r维Riemann流形,b>0,φ,λ是B上的光滑函数, 且满足
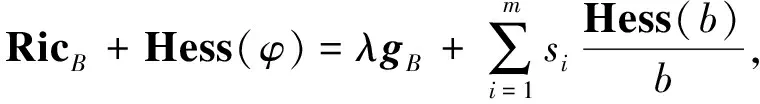
(5)

(6)
其中si≠0为实数.则

(7)
其中μ∈为常数.
证明: 对式(5)求迹, 有
这里R是B上的数量曲率.因此

(8)
另一方面, 对式(5)求散度, 并利用div(Hess(ψ))=Ric(ψ,·)+d(Δψ), 得
又因为
所以式(9)可转化为
利用第二Bianich恒等式的缩并, 即

(11)
将式(8)和式(10)代入式(11), 得
对式(6)求微分, 得

(13)
即
证毕.


(14)

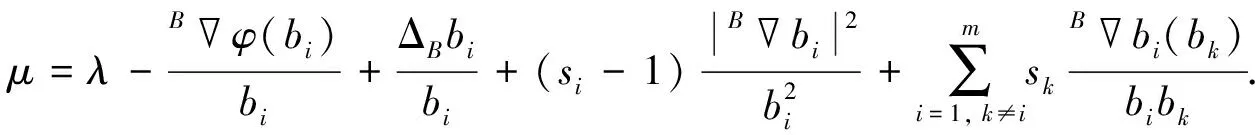
(15)

所以在基流形B上可得
从而式(14)得证.下面用类似的方法证明式(15).
由引理3中结论4)和式(1), 对任意的V,W∈L(Fi), 1≤i≤m, 有

将式(17)代入式(16)得
由性质2, 并令式(7)中b=bi(1≤i≤m), 可得
其中μ为常数, 满足
证毕.
性质3中若bi=b(1≤i≤m), 其中bi是B上的光滑函数, 则可得下列推论.


4 主要结果的证明
4.1 定理1的证明
由推论2, 必要性得证.故只需证明充分性.
首先, 设(Mn=Br×bF1×bF2×…×bFm,g)是多重卷积流形.由引理3中结论1)和式(5)知, 对任意的X,Y∈L(B),Mn满足式(1).
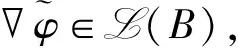

(18)
由引理3中结论2)和式(18)知,Mn满足式(1).此外, 对于任意的V∈L(Fi),W∈L(Fj)且i≠j, 有

(19)
所以由引理3中结论3)和式(19)知,Mn满足式(1).

由式(17)知,


4.2 定理2的证明
在基流形B上定义一个二阶椭圆算子:
则式(7)等价于
对于条件2), 因为p,q分别是B上函数b的最大值点和最小值点,λ≤0且λ(p)≤λ(q), 所以Bb(p)=0=Bb(q)且ΔBb(p)≤0≤ΔBb(q).又因为b>0且λ(p)≤λ(q), 所以-λ(p)b2(p)≥-λ(q)b2(q), 再结合式(7)得
0≥b(p)ΔBb(p)=μ-λ(p)b2(p)≥μ-λ(q)b2(q)=b(q)ΔBb(q)≥0.
因此
μ-λ(p)b2(p)=μ-λ(q)b2(q)=0.
下面对λ(p)分两种情形讨论.当λ(p)≠0时, 由λ(p)≤λ(q)<0得
因此b(p)=b(q), 即b是常数; 当λ(p)=0时, 由λ(p)=0得μ=0, 又由式(7)可得
最后由强最大值原理知b是常数, 且由式(7)得λ=0.
因此,Mn是一般的多重Riemann积流形上的梯度Ricci孤立子.定理2证毕.
