关于Hermitian矩阵序关系的一些注记

翟成波，金志香

（山西大学 数学科学学院，山西 太原 030006）

0 引言

众所周知，非线性矩阵方程在动态规划、阶梯网络、控制理论、随机滤波、统计学、工程等领域有着重要的应用，而非线性矩阵方程的正定解起着决定性的作用，引起了许多学者的研究兴趣。关于正定解的讨论，我们主要围绕正定解的存在性和唯一性的充分和必要条件、求解正定解的迭代算法、正定解的扰动分析三个方面展开。在前两个方面中，我们发现在一些文献中关于半序Banach空间Hermitian矩阵序关系的某些不等式是错误的。因此，在这些文献中，也得不到相应的结论。

本文主要研究在一些文献中关于半序Banach空间Hermitian矩阵序关系的不等式。第1节给出准备工作和主要结论；第2节给出主要结论的证明；第3节给出数值例子来说明我们的结论；第4节给出本文的结论。

1 准备工作

回忆锥的基本知识［1］。设 (E，||·||)是一个实Banach空间，通过E上的一个锥P定义半序关系。也就是说，对x，y∈E，我们有x≤y当且仅当yx∈P。我们记x≪y如果y-x∈，这里表P的内点集。如果非空，我们称P是体锥。

记Mn为n×n复矩阵构成的集合，Hn为n×nHermitian矩阵构成的集合，Kn为n×nHermitian半正定矩阵构成的集合，Pn为n×nHermitian正定矩阵构成的集合。在文献［2］中，Hn中定义谱范数 ||·||，则Hn是实 Banach 空间，以及Hn通过锥Kn定义半序关系并且Pn=n。A≥0(A＞0)说明A∈Kn(A∈Pn)。A≥B(A＞B) 说 明 对A，B∈Hn，有A-B∈Kn(A-B∈Pn)。在文献［3-8］，也可以得到上述表示。在文献［9］中，作者给出以下结论。

引理1正定矩阵A∈Mn与Hermitian矩阵B∈Mn的乘积是可对角化矩阵，它的所有特征值都是实数。矩阵AB和B有相同数目的正，负特征值和零特征值。

本文研究半序Banach空间中Hermitian矩阵序关系的一些不等式，得到以下定理。

定理若A，C∈Hn，B∈Pn，A≥C，很难得到BA≥BC，除非B与A-C可交换。

2 主要结论

在这一节中，给出在一些文章中关于半序Banach空间Hermitian矩阵序关系的不等式，指出问题所在并进行分析。下文公式中*表示转秩运算。

在文献［3］中，Erfanifar等人提出一个新的免逆不动点迭代策略去获得非线性矩阵方程

的最大正定解。即

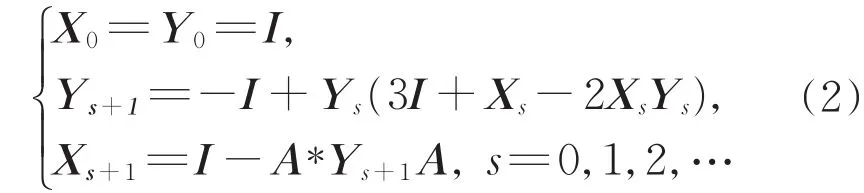
得到了方程（1）可解性的充分必要条件，见以下引理。

引理2若Xs和Ys是由算法（2）产生的，则

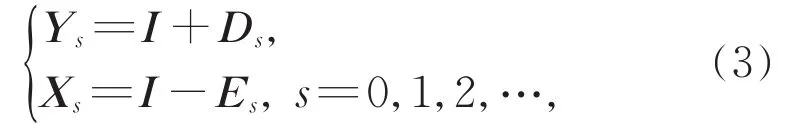
其中Ds和Es是半正定矩阵，并且有Es≥(I+Ds)-1Ds。

用归纳法证明上述引理的过程中，假设（3）对s=k成立，即Dk和Ek是半正定矩阵，并且有Ek≥(I+Dk)-1Dk，需要证明s=k+1成立。在Erfanifar等人证明过程中，对于一些句子的表述中，有一些不妥之处。第一句是“Using to theEk≥(I+Dk)-1Dk，(I+Dk)Ek-Dkis a semipositive definite matrix”，第二句是“we haveDk≤Dk+1andEk≤Ek+1… and thenDk+1Ek≤Dk+1Ek+1。”

注1在第一句中，从Ek≥(I+Dk)-1Dk得Ek-(I+Dk)-1Dk是半正定矩阵。即要证明

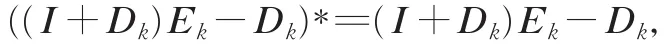
且(I+Dk)Ek-Dk有非负特征值。通过计算得

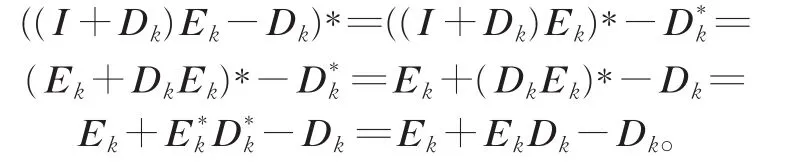
若Dk和Ek可交换，则有

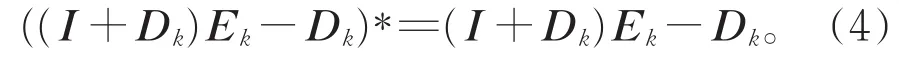
但是Dk和Ek可交换性不明确，所以很难得到（4）式。即(I+Dk)Ek-Dk不是Hermitian矩阵，更不是Hermitian正定矩阵。

从以上的讨论中，得到了定理，现给出证明。

定理的证明从上述分析中，得知定理的条件满足时得不到BA≥BC。若B与A-C可交换时，(BA-BC)*=(BA)*-(BC)*=A*B*-C*B*=(A-C)B=B(A-C)=BA-BC。

通过引理1及A≥C得BA-BC与A-C有相同数目的非负特征值。即BA≥BC。定理得证。

注 2第二句考虑“we haveDk≤Dk+1andEk≤Ek+1…and thenDk+1Ek≤Dk+1Ek+1”这个结论不是很容易得到。根据引理 2 中的Dk≤Dk+1，Ek≤Ek+1，Dk，Ek，Dk+1，Ek+1是半正定矩阵得Dk+1Ek+1-Dk+1Ek是半正定矩阵。首先，

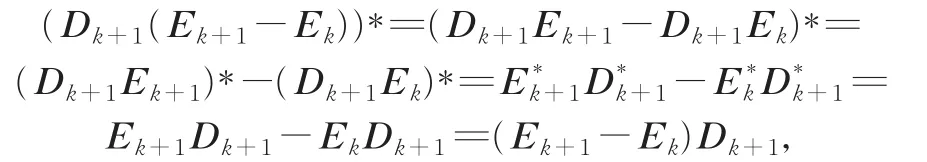
除非Ek+1-Ek与Dk+1可交换，则Dk+1Ek+1-Dk+1Ek不是Hermitian矩阵，更不是Hermitian正定矩阵。

在一些文献中也出现类似于定理结论，见文献［10-11］。接下来给出详细的解释说明这些结论的不正确性。

是Hermitian半正定矩阵。由于Xk与Yk是否可交换不明确，从而(I-Xk)Yk-(I-Xk-1)Yk-1不一定是Hermitian矩阵。从而很难得到Yk+1=(I-Xk)Yk+I≥(IXk-1)Yk-1+I。

注 4在文献［11］的定理2中，Ali等人通过Q1，Q2≥I得到Q1≤Q1Q2。这里需要说明Q1Q2-Q1是Hermitian矩阵。现在

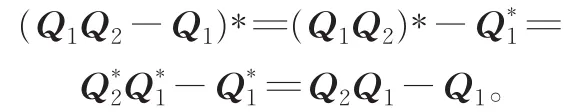
只有当Q1和Q2可交换时，才有(Q1Q2-Q1)*=Q1Q2-Q1。然而Ali等人没有假设这一条件，故得到Q1≤Q1Q2是不合理的。

注5在文献（［12］）的引理2中，张等人得到有关定理结论，见下述引理。

引理3对于对称半正定矩阵A和D，对称矩阵B和C，若满足AC=CA，BD=DB，AD=DA，A≥B，C≥D，则有AC≥BD。

从上述引理中，可以说明在一些文献中半序Banach空间关于Hermitian矩阵序关系的不等式不是很简单就得到的。此外，文献中的B≥A说明B-A是Hermitian矩阵且B-A的特征值是非负的。然而在一些文献中，并没有这样考虑。例如文献（［3］），见下述引理。

引理 4若Xs和Ys是由算法（2）产生的，则YsXs≤I，s=0，1，…，和Ys≤X-1s。

在引理4的证明过程中，必须说明I-YsXs是Hermitian矩阵且I-YsXs的特征值是非负的。然而，不能保证I-YsXs是Hermitian矩阵因为Xs与Ys是否具有交换性不明确。

3 数值例子

这一节将给出一个例子说明定理的结论。

4 结论

本文主要针对半序Banach空间中关于Hermitian矩阵序关系的一些不等式的错误，给出了注记。为了说明半序Banach空间中关于Hermitian矩阵序关系的一些不等式，矩阵的交换性是必须要考虑的条件。