《加法交换律和乘法交换律》教学设计
2021-11-02利燕妮
文|利燕妮
【教学内容】
北师大版四年级上册第四单元。
【教学过程】
一、情境引入
师:同学们,今天让我们来一次数学探秘之旅。
师:(课件出示问题)请用两种方法进行列式计算。
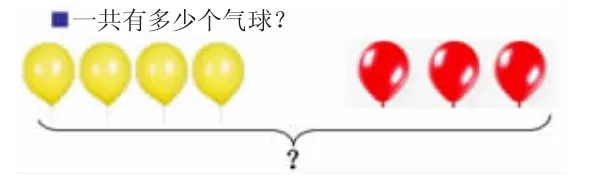
生:4+3=7,3+4=7。
板书:

师:仔细观察这组算式,你发现了什么?
生:左右两边的算式都等于7,得数一样。
生:两边的数字交换了位置,符号不变,数字不变。
师:同学们善于观察,真了不起。其实,我们还可以从加法的意义上去理解它,你想到了吗?
师:比如4+3 表示的是先数4个黄气球再数3 个红气球,一共是7 个气球。
师:3+4 表示什么?
生:表示先数3 个红气球再数4 个黄气球,一共是7 个气球。
(板书:先数……再数……)
师:不管怎么数,左右两边的算式结果是一样的。
【设计意图:关注“数数”活动,关键让学生理解加法的意义,初步感悟加法交换律的道理。学生在“数数”的过程中,明白4+3=3+4 虽然是两个不同的过程,但结果是相同的。】
二、结合下面的例子,你能说说等式为什么成立吗?
35+42=42+35

(学生独立思考再合作交流)
生:35+42=77,42+35=77,所以等式是成立的。
师:谁有补充?
生:35+42 表示从学校出发,学校到电影院之间的距离;42+35表示从电影院出发,电影院到学校之间的距离。
生:我发现不管从学校到电影院,还是从电影院到学校,它们都是两点之间的距离。
师:刚才同学们不仅从算式的结果上进行了验证,还会结合这个图去解释算式成立的理由,真了不起!
【设计意图:从学生的生活经验入手,关注“数形结合”,渗透数学基本思想。例子中,主要让学生在观察路线图中,感悟从电影院到学校的距离和从学校到电影院的距离是一样的。让学生在观察路线图和表达中经历“数数”过程,感悟加法交换律的探索过程,让学生从现实背景出发认识加法交换律。】
三、你能利用生活中的事例解释你的发现吗?
(学生独立思考、把发现写下来后再和同桌合作交流)
(展示学生作品,让学生上台说一说自己的发现)
生:我们班有31 个男生、25个女生,那我们班一共有多少人?我们可以先数男生31 人,再数女生25 人,即31+25=56(人);也可以先数女生25 人,再数男生31人,即25+31=56(人),不管怎么数,我们班的总人数都是56 人,所以25+31=31+25。
生:一件上衣35 元,一条裤子30 元,我要买一套衣服多少元?我们可以先算一件上衣35元,再算一条裤子30 元,即35+30=65(元);也可以先算一条裤子30 元,再算一件上衣35 元,即30+35=65(元);不管怎么去计算,一套衣服的总金额不变,即35+30=30+35。
【设计意图:应用意识是由意识利用数学的概念、原理和方法解释现实世界中的现象,解决现实世界中的问题。设计的这个问题,主要是为了激发学生已有的生活经验,让学生在现实世界中感悟加法交换律,启发学生展开联想,举出更多的实例,培养学生的应用意识。】
四、用a、b 代表两个数,你能写出上面发现的规律吗?
生:a+b=b+a。(板书)
【设计意图:用字母表示加法交换律,这是数学的符号世界提出问题的重要形式。《数学课程标准(2011年版)》指出:符号意识主要是指理解并运用符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理,得到的结论具有一般性。建立符号意识有助于学生理解符号的使用是数学表达和进行数学思考的重要形式。因此,用字母表示加法交换律,可以让规律更容易、更准确、更简明、更有效。】
五、猜想:乘法、除法、减法也满足交换律吗?
(学生独立思考再合作交流)
师:我们先从乘法开始,谁来说一说?
生:3×2=2×3,左边算式等于6,右边算式也等于6,所以乘法成立。
(教师顺势画出点子图)

师:你可以从乘法的意义上说吗?
生:一排有3 个,有2 排,有2个3,所以3×2=6。
师:嗯,你是横着数的,对吗?还有不同的数法吗?
生:我们还可以竖着数,一列有2 个,有3 列,表示有3 个2,所以2×3=6。
师:同学们真是善于观察和表达,是不是所有的乘法算式都满足交换律呢?谁还能举例验证一下?
生:5×6=6×5,左右两边算式都等于30。
生:8×9=9×8,左右两边算式都等于72。
……
师:同学们,刚才在举例验证中发现:在乘法中是满足交换律的。我们可以把这样的规律取个名字,谁能试一试?
生:乘法交换律。
(板书:乘法交换律)
师:是的,同样用a、b 代表两个数,你能写出上面发现的规律吗?
生:a×b=b×a。
师:同学们太棒了,不仅可以举例验证发现规律,还能用字母表示规律。那在除法算式中满足交换律吗?谁来说一说?
生:3÷1 不等于1÷3,3 个苹果平均分给1 个人吃,每人3 个苹果;1 个苹果分给3 个人吃,每个人分不到一个苹果。
师:你说得很有道理,还有吗?
生:10÷5=2,可是5÷10=0.5,结果很明确,除法交换律不成立。
生:9÷3=3,3÷9≠3?除法交换律不成立。
生:老师,我发现5÷5=5÷5,就是被除数和除数一样的时候,除法交换律成立。
师:嗯,真会思考,你还举了一个特殊的例子。大家来看看这些例子,你觉得在除法中交换律成立吗?
生:不成立的,5÷5=5÷5 仅仅是一个特例,不能说明所有的除法都成立的。
师:是的,我们在举例证明中只要能找到一个不成立的例子,就能证明结论不成立。
师:那在减法算式中满足交换律吗?谁来说一说?
生:10-3=7,3-10=-7,所以减法不满足交换律。
师:你还知道负数,真了不起。还有吗?
生:3-1=2,1-3 不等于2,所以减法不满足交换律。
师:现在我们来回顾一下,在加减乘除算式里,只有加法和乘法满足交换律,除法和减法是不满足交换律的。
【设计意图:基于学习加法交换律的基础上,打开学生思维,让学生利用迁移的方法,大胆尝试在写算式举例子的验证中去发现结论。这个过程留给学生足够的时间和空间自主地去探索发现,教师要引导学生学习用反例来推翻猜想的方法:针对一个猜想,如果举不出一个反例,不能证明结论一定成立;而反过来,如果能举出一个反例,就能推翻这个猜想。这也是一种证明的方法,由此培养学生的推理能力。】
六、思考:在生活中,是不是所有事情都可以交换呢?
(学生独立思考再合作交流)
师:谁能给大家分享一下你的思考呢?
生:我们都是先穿袜子,再穿鞋,如果先穿鞋再穿袜子的话,那不就闹笑话了吗?
生:我们在煮饭的时候,都是先洗米再煲饭,而不能先煲饭再洗米。
师:是的,在生活中,并不是所有的事情都可以交换的,在数学中也是一样的,只有乘法和加法才满足交换律。
【设计意图:在现实世界里,大多数的动作是不能交换的。让学生感悟“交换”不是容易做到的,满足交换律是需要证明的一种特殊情况。】
七、下表是笑笑三次跳绳的成绩,你能帮她统计总分吗?
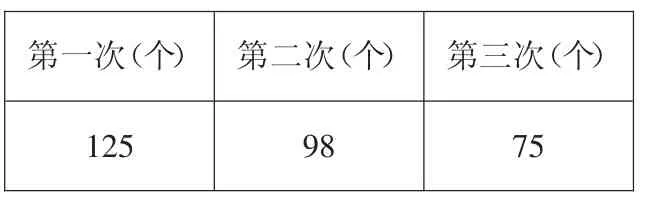
第一次(个) 第二次(个) 第三次(个)125 9875
(学生独立思考再合作交流)
师:谁来说说你的方法?
生:我觉得是先算第一次和第三次的次数,再算第二次的次数。
师:你能说说理由吗?
生:因为第一次和第三次合起来是200 个,刚好是整数,这样方便计算。再算200+98=298(个)。
板书:
125+98+75
=(125+75)+98
=200+98
=298(个)
师:嗯,你真会思考!同学们,我们的计算会不会改变总分呢?
生:不会,不管先算第一次和第二次,再算第三次,还是先算第一次和第三次,再算第二次,我们计算的都是第一次、第二次和第三次的总分。
师:你真善于总结,这也是我们为什么要学习运算律的奥秘,这样有利于我们进行简便运算。
【设计意图:本题目的设计主要让学生在学完加法交换律后,让学生感悟加法交换律的运用,感悟可以运用运算律进行简便运算。在练习、交流、探讨中拓展学生思维、培养学生运用知识的能力。】
八、今天你学到了什么?
【设计意图:让学生自己去梳理和总结新知,让新知得到升华和内化。】
(“第十三届小学教学特色设计大赛”获奖作品选登)
