顺逻辑而教 依心理而学
——以《平行与垂直》教学为例
2021-11-02冯舒莹
文|冯舒莹
《平行与垂直》是小学数学的经典课例,研究的教师比比皆是。在《小学教学设计》2020年11月刊“典型课例”栏目中就刊登了张森、居晓红老师关于这节课同课异构的两篇课例,著名特级教师刘松对这两节课进行了深度点评,阅读下来感悟很深。张老师借助智慧课堂技术,致力于发展学生的空间观念;居老师从学生知识起点出发,引导学生经历数学抽象的学习历程。仔细分析两位老师的课堂,除了都是精彩纷呈、各有巧思之外,还有一个最大的区别:张老师先教平行后教垂直,居老师则先教垂直后教平行。对此,刘松老师在点评中这样说:“基于儿童视角,平行与垂直这两个抽象概念中垂直更直观可检验,学生会更容易掌握,但人教版等教材均是先学平行(不相交)后学相交和特例(垂直),这不是教学设计的绝对顺序,也不是课堂教学的唯一选择。”
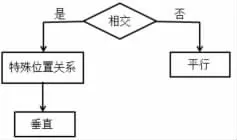
平行与垂直是并列的两个概念,不同的教学顺序具体有怎样的区别呢?为了弄清楚这个问题,根据张老师和居老师的课例,我整理出两种教学流程:

同一平面内两直线的位置关系可分为相交、不相交与重合。相交研究两直线的角度,不相交(平行)研究两直线间的距离,重合既没有角度也没有距离,因此一般不研究。
两种教学顺序都抓住了同一种重要但学生易混淆的模型,即看似不相交但延长后会相交的两直线,以凸显平行与垂直的最大区别——相交,以“相交”为概念起点,之后教学顺序走向分流。下面分别摘录了张老师和居老师课例的教学片断,试图分析两种不同顺序的教学逻辑。
【教学片断1】
师:③号图形看似不相交,实际则相交。那④号图形延长后,会不会相交?
(学生猜想后,在平板电脑上验证)
师:无限延长都不会相交吗?
生:都不会。
师:除了延长,是否会相交还可以怎么看?
生:还可以看它们之间的距离。
通用多学科资源服务平台国外主要在图书、期刊,大型出版集团或期刊社起家,历史悠久,基本在百年以上,兼顾数字出版与传统出版;国内知网主要在期刊、工具书、年鉴等,万方主要在学位、期刊、方志等,维普主要在期刊、超星主要在图书、期刊。国内主要以数字出版集成服务商起家,历史在30年内,发展后进行了部分纸质期刊的布局。
师:通过刚才的分类辨析,我们知道同一个平面内,两条直线的位置关系分为相交和不相交两种。不相交的这两条线叫做平行线。
在学生已经猜想验证两条直线是否相交后,张老师直接验证平行,前后任务衔接非常自然,学生能马上猜想操作,思维没有停滞,这是因为这一过程符合逻辑。判断平行与垂直的钥匙在于“相交”。由“相交”到“垂直”的过程需经历寻找特殊位置关系的一步,不能直接跳跃到“垂直”。而到“平行”却只要否定就能直接指向目标。以“相交”为判定标准,按照教材从否定方向推出“平行”的概念,思维可以一步到位,遵循的是一种更加简洁明晰的逻辑顺序。
【教学片断2】
教师讲解“相交”和“交点”的概念。
师:仔细观察这五组相交的直线,你发现了什么相同点和不同点?
生1:每一组直线都相交,都有一个交点。
生2:两条相交的直线会形成一个角,每一组角的大小都不同。
学生验证直角,教师小结垂直的概念。
居老师是为数不多先教垂直的。找相交直线的不同时,学生马上分析角度不同,抓住了垂直的本质,这是因为角与角度是学生已有的认知,学生在本册第三单元刚学过角的度量,对再次出现的角度比较敏感,能马上调动起相关经验,对平行则较为陌生;从操作简易程度来说,相较于验证平行要测量距离,验证垂直仅需一把三角尺或量角器,操作时学生更为轻松、迅速,表达时更加自如、规范,能将抽象的概念层层内化。同时,按照皮亚杰同化与顺应的理论,新知识的学习可以被旧知识包容,也可以顺着已有知识延伸生长,由熟悉的“相交”“直角”到新知识“垂直”,符合学生的认知规律。
结合上述分析可以发现,两种教学顺序分别从教学内容的内在逻辑和学生心理特点、认识能力两方面考量,安排教学顺序,看似过程相左,实则殊途同归。
教学顺序是教学逻辑的体现,数学是一门逻辑性很强的学科,知识体系具有严谨的系统性,故而数学教学的逻辑非常重要。因此,依据以上分析与思考,结合数学知识逻辑和学生心理发展的特点,笔者认为在数学教学时应该处理好以下三种关系:
1.各个教学内容之间的逻辑关系。
在教学图形与几何时,不能割裂地看待各个教学内容,不仅要注重对每一个教学内容的准确理解,还要关注该教学内容在整个知识系统中的位置以及它们之间的关系。这种关系一方面体现在一节课的教学内容在其所处的学科知识中的结构关联性;另一方面体现在前后教学内容之间的联系上。以点、线、面、体的逻辑关系为例,点动成线,线动成面,面动成体,四者关系密切。但因为课时、学段、教学内容的划分等多种原因,无法一次性连贯地把相关知识教授完毕,那么在教学相关内容时,应有意识地互相渗透、互相沟通。
2.教学内容自身的逻辑关系。
教学内容不管是陈述性知识还是程序性知识,都需关注其自身的逻辑关系,学生以这种逻辑将新知识融合匹配到原有的认知结构中。以《平行与垂直》为例,“相交”就是知识点之间的逻辑连接,不能跳过“相交”孤立地来看“平行”“垂直”,故本课所有课例都先抛出相交的概念,借由这一逻辑连接,后续知识才能一一衔接,学生的知识体系才能环环相扣、越来越完善。
计算教学同样也有自身的逻辑关系,以乘法为例,乘法以同数连加为现实模型,各个版本教材都是以加法作为逻辑连接,浙教版教材更是在一年级连续教学加法与乘法。这告诉我们对数学内容的理解要环环相扣、层层递进,切不可跳跃式教学。
3.学生心理特点和认知能力与教学顺序的关系。
学生是教与学互动中的主体,教学顺序要依据学生的心理特点和认知发展规律,遵循由简单到复杂、由具体到抽象、由低级到高级螺旋上升的过程。教学中要处理好学生心理特点和认知能力与教学顺序的关系。第一,要考虑同一学生在不同阶段呈现的心理特点和认知能力。第二,要照顾学生群体间认知水平的差异,制定个性化难度适宜的教学活动,因材施教。
以上对《平行与垂直》教学顺序的思考,提醒我们:课堂教学不仅要理清教学的逻辑,也需要关注学生的心理特点,顺逻辑而教,依心理而学,才能事半功倍。
