三～六年级学生分数概念的错误理解及其发展

巩子坤，杨 婷，张 都，周心怡

三～六年级学生分数概念的错误理解及其发展

巩子坤1，杨 婷2，张 都3，周心怡4

（1．杭州师范大学 经亨颐教育学院，浙江 杭州 310012；2．浙江工业大学附属实验学校，浙江 杭州 310014；3．余杭区闲林中学，浙江 杭州 310000；4．杭州市新华实验小学，浙江 杭州 310015）

基于分数的7个子概念，采用4套包含式问卷，选取306名三～六年级学生，考察其分数概念的错误理解类型及发展趋势．结果发现，三～六年级学生出现的主要错误是：错误理解“等分”概念，错误理解“单位量”概念（包含3个子类型），不会用数线表示分数与错误理解“等值分数”概念（包含3个子类型）等8类错误；其中6类错误的错误率峰值出现在四年级，两类出现在五年级．重要的顽固型错误是：四年级学生错误理解“等分”概念；五年级学生错误理解“单位量”“分数在数线上的表示”概念．建议：在四年级适当加入分数内容；提高三年级“等分”“单位量”概念、五年级“分数在数线上的表示”概念的教学比重；教师应当对8类主要错误有针对性地进行教学．

三～六年级学生；分数概念；错误理解类型

1 问题提出

“分数”是小学数学核心概念之一，也是小学教学中重要且困难的知识．说其重要，是因为分数将小学阶段的整数、小数、比例、四则运算等知识融会贯通了．说其困难，是因为分数包含许多子概念，如单位量概念、平均分概念、等值概念等；是因为可以从不同的角度来理解分数，如部分与整体、算子、商等[1–2]；是因为学习分数时涉及两种情境量，连续量情境和离散量情境．诸多因素组合交织在一起，导致学生难以正确理解分数概念．因此深入分析学生构建分数概念过程中出现的错误及其原因，对于帮助学生正确地、系统地建构分数知识乃至关于数的知识体系至关重要．

国内外诸多学者对此进行了研究．吕玉琴[3]对等分概念的错误类型进行研究，发现学生在离散量和连续量中都会出现错误．李仙苹[4]、刘爱东[5]发现学生误认为“平均分”后的各部分大小、形状等都要相等，并且对于已经给出的“平均分”图形，不能进行整合．刘丹丹[6]也指出学生不仅在等分概念中存在错误，对于单位量概念也模糊不清．Figueras[7]指出学生在确定单位量时出现的错误有：忽略条件中给定的单位量、只受分子（母）影响．刘春晖、辛自强[8]采用Stafylidou和Vosniadou编制的分数任务，考察了五～八年级学生在分数表征的3个层次出现的错误类型：整数偏向现象（将分数表征为两个互相独立的自然数）、对单位“1”理解有误以及过分重视“部分—整体”概念中的整体[9]．国外众多学者如Behr[10]、Mark[11]、Hunting[12]等人指出：由于缺乏等值分数概念，学生在解决分数问题时会把分子和分母看作是两个不相关的整数，而不是把分数看作一个数，所以在比较大小时会出现多类错误．汤锦云[13]研究了学生在数线上表示分数时出现的错误．虽然，国内外有关于分数相关概念错误类型的研究，但是，这些研究比较零散，缺少对分数众多概念错误类型的整体研究，并且目前较少有学者对学生的错误类型进行发展研究．

基于《义务教育数学课程标准（2011年版）》（简称《数学课程标准》）[14]，人教版小学《数学》教材中分数的学习安排如下．三年级初步认识分数，主要学习等分、单位量、分数表征、分数的比较和分数运算（同分母分数加减）这5类分数概念；五年级增加了等值分数、分数在数线上的表示、分数与除法的联结这3类分数概念；六年级安排了分数作为比值的意义这一概念．由于分数运算与分数概念学习关联性不强，分数作为比值的意义仅在六年级学习，因此，对分数的7个子概念进行整体研究（依次为等分、单位量、分数表征、分数比较【三年级学习】、等值分数、分数在数线上的表示、分数与除法的联结【五年级学习】），研究问题是：（1）学生在学习分数概念时会产生哪些类型的错误？（2）这些错误是怎样发展变化的？

2 研究设计

2.1 研究对象

在杭州市某小学三～六年级中，从每一个年级随机选取两个平行班级共306名学生（三年级84人，四年级84人，五年级69人，六年级69人）作为被试；分别对各年级平行班的期末成绩进行方差分析与多重比较，结果显示，同一年级的各个平行班之间均不存在显著性差异（所有的>0.05）．问卷调查和访谈均在这些班级进行．

2.2 研究方法

根据研究目的、研究问题以及现实条件，以文献分析法、问卷调查法为主，以访谈法为辅来探查学生关于分数概念的错误理解．

2.3 研究工具

2.3.1 问卷结构

基于文献综述，将分数概念分成7个子概念[2-6，8，11-12]，依据《数学课程标准》以及人教版小学数学教材，编制了4套问卷，分别对应三～六年级．4套问卷为包含关系（较高年级的问卷包含了较低年级的问卷），比如，四年级的问卷包含了三年级问卷的所有题目，并增加了几道题目，题号以低年级为准，如“三–4”表示的就是三年级的第4题，四、五、六年级也都是同一道题目．

2.3.2 问卷信度

以Cronbach’s系数为指标，考察4套问卷的信度，系数均大于0.8，说明问卷信度较好．

2.4 错误分类与编号

首先，通过问卷分析，根据错误原因总结出学生关于分数的7个子概念的错误类型．第一个子概念的第一类错误记为11，第二类错误记为12；第二个子概念的第一类错误记为21，依次类推．

其次，对不同年级同一子概念的同一类错误的错误率进行卡方检验．发现一些错误在不同年级间存在显著性差异，为便于讨论，将这类错误界定为非顽固型错误，其中，部分错误的错误率会随年级升高显著降低，属于非顽固型可消除错误；部分错误的错误率不会随年级升高显著降低，属于非顽固型不可消除错误．一些错误类型在不同年级间不存在显著性差异，将之界定为顽固型错误．

主要错误是指平均错误率高于15%的错误，或者是顽固型错误．如果一类错误既是平均错误率比较高的错误，又是顽固型错误，将之界定为重要错误．

3 结果与分析

3.1 “等分”概念的错误类型及发展

“等分”就是把一个整体平均分成几份．

三–1：下列选项中，虚线是分割线，哪几个图形是大小等分的等分图形，请选出来（）．

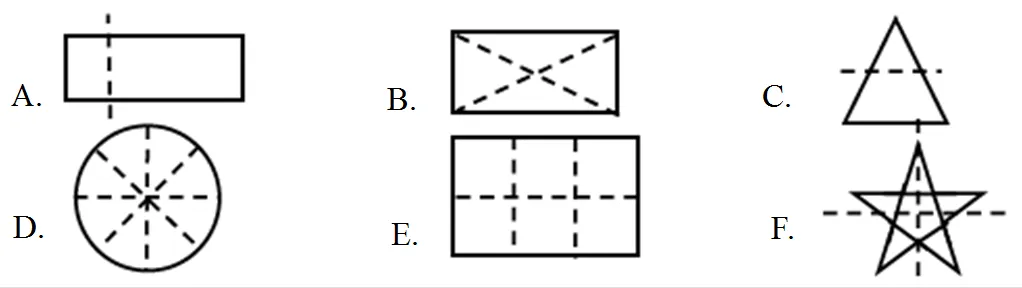
类型11：认为等分必须面积相等、形状相同．例如，因为B项中4个三角形不全等而漏选B．

类型12：未能理解等分概念的内涵．例如，选择A或C，而A、C项显然未等分．

类型13：凭感觉盲目判断．例如，选择F，F选项看似等分，实则未等分．

类型14：离散量情境下等分概念的认知缺失．例如，G、H选项为离散量情境，由于数量、大小不相等而未等分．

综上所述，对于等分概念学生出现4类错误，按其错误率进行综合分析，如图1所示．

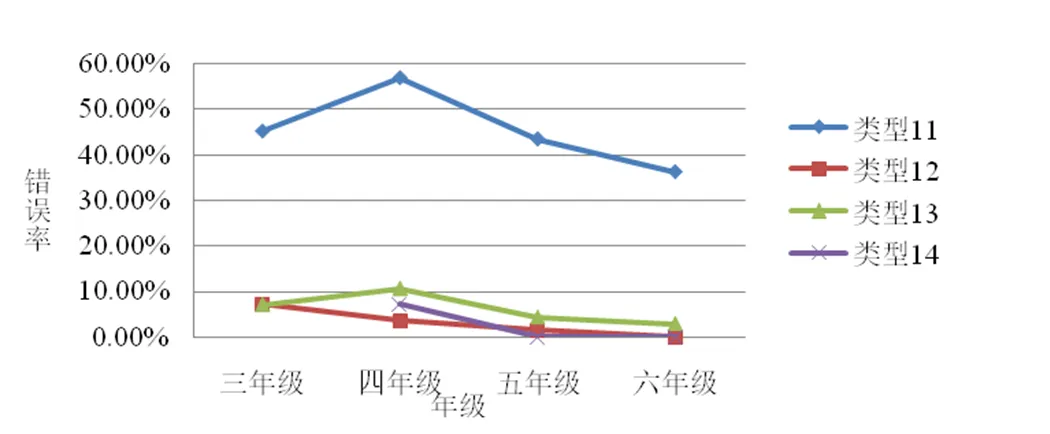
图1 “等分”概念不同错误类型的错误率

分析可以得出以下结论．

（1）无论是哪个年级，类型11平均错误率最高，并且远高于其它3种类型．

3.2 “单位量”概念的错误类型及发展

在小学数学中，“单位量”通常是指分数中的整体“1”，可以表示一个物体，也可以表示一些物体．“整体”可以表示物体的全部，也可以表示物体的一部分，根据所观察的对象发生变化，具有相对性．

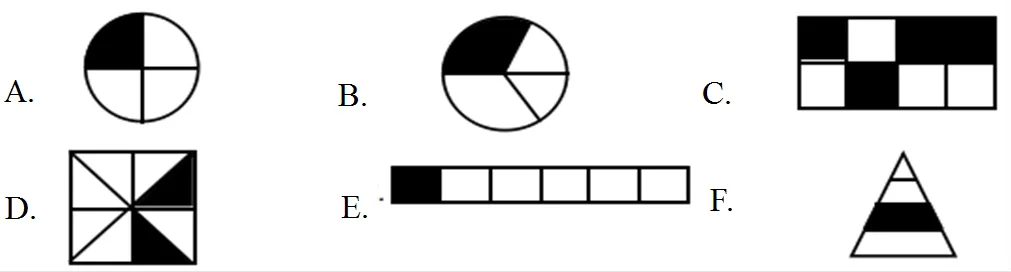
类型21：不能将图形进行整合．例如，漏选D．

类型23：受分母的影响，认为分母是几，图中就有几个黑色的部分．例如，选择C，C选项中有4个黑色小正方形，对应分母中的“4”．

类型24：受分子的影响[13]，认为分子是几，图中就有几个黑色的部分．例如，选择E，E选项中有1个黑色小正方形，对应分子中的“1”．

通过分析，还发现了另外两类错误．

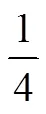
A. 正确 B. 不正确 C. 无法确定

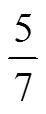
类型28：缺少对单位量的认知．例如，选择C．

综上所述，对于单位量概念学生出现8类错误，按其错误率进行综合分析，如图2所示．

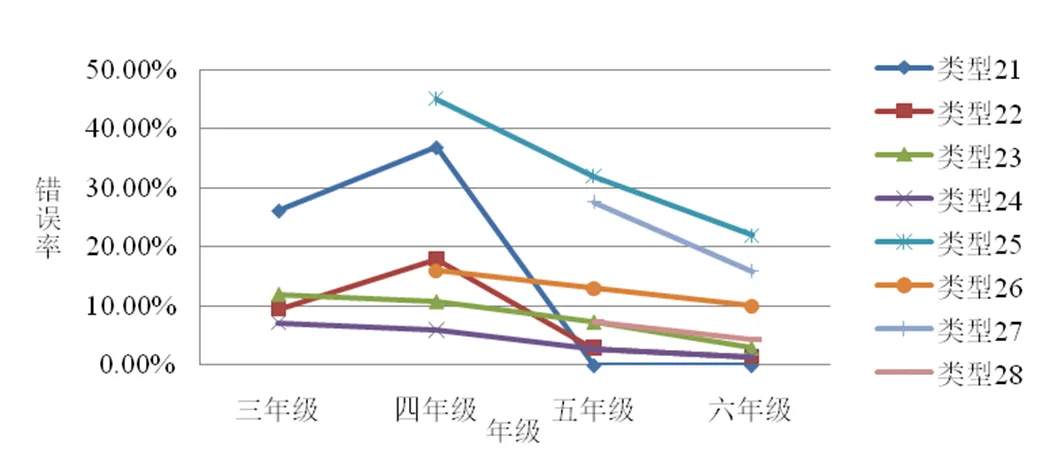
图2 “单位量”概念不同错误类型的错误率

分析可以得出以下结论．

（1）在这8类错误中，类型21、类型25、类型26、类型27错误率较高，其余4类错误率较低．

3.3 “分数表征”概念的错误类型及发展

分数表征主要包括符号表征和图象表征[15–16]．

3.3.1 符号表征

符号表征，即给出图形，要求学生根据图形中的涂色部分写出相应的分数[15]．

三–3：用分数表示下列图形中的黑色部分．

首先分析三～六年级A、B、C项的答题情况，统计发现只有B项出现错误．

类型31：将相连图形看作一个整体，不能拆分．例如，将B项中两个相连的黑色小三角形看作一个三角形．

再分析四～六年级的D项的答题情况．

类型32：不能将图形进行整合．例如，未能将D选项中黑色部分旋转整合成一个半圆．

三–5：用分数表示图中黑色部分，并比较两个分数的大小，在□里填写“＞”、“＜”或“＝”．

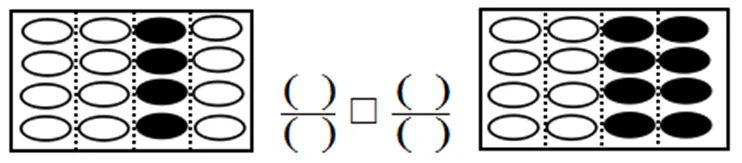
学生的错误类型有两种．

类型33：将分子和分母看作两个数，分子为涂色部分，分母为未涂色部分，如图3．

图3 类型33

类型34：分子与分母位置颠倒，如图4．

图4 类型34

三–6：看图写分数．

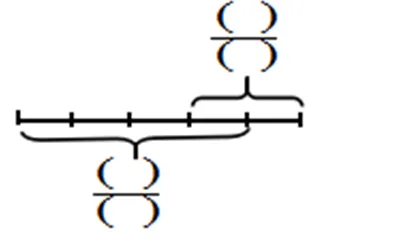
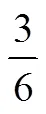
综上所述，学生出现5类错误，按其错误率进行综合分析，如图5所示．

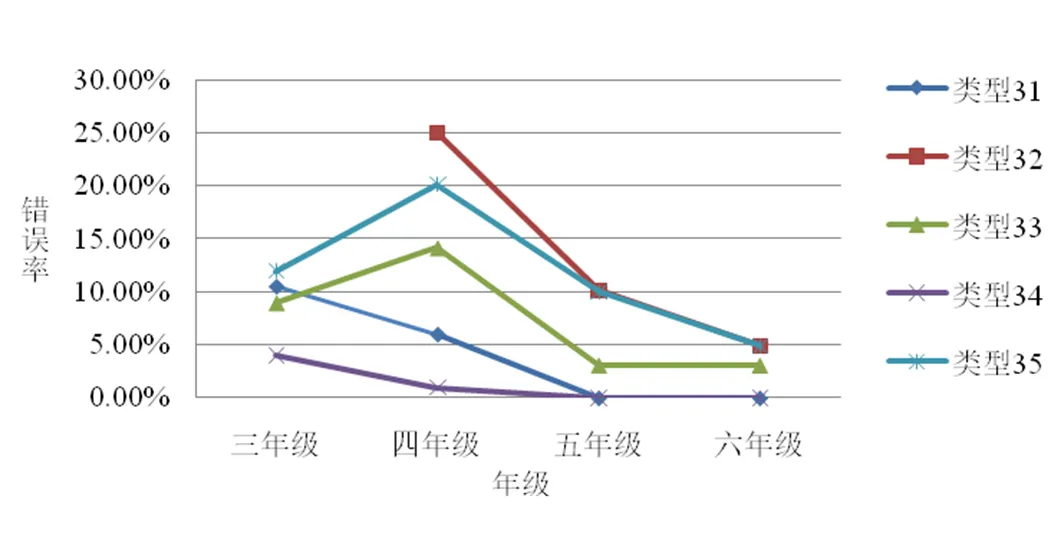
图5 “分数符号表征”概念不同错误类型的错误率

分析可以得出以下结论．

（1）在这5类错误中，平均错误率最高的为类型32，其次为类型35，其余类型的错误率较低．

3.3.2 图象表征

图象表征，给出分数，要求学生根据所给的分数对图形涂色[16–17]．

三–8：看分数，涂颜色．

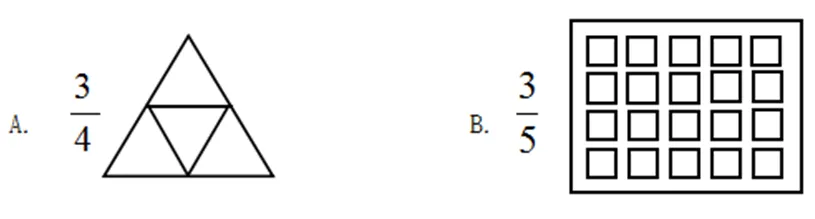
学生关于B项所表现出来的错误类型有两种．

类型36：认为分数中的分子所表示的是“物体的个数”．例如，只涂3个小正方形．

类型37：认为分子是几就涂几行．例如，只涂了3行．

再分析五、六年级的C、D两项．C、D两项是在离散量情境下，每个部分又分成几个小部分，将其定义为“离散连续混合情境”．

类型38：离散连续混合情境下概念认知缺失．例如，认为分子是多少就涂几个小方块．

综上所述，对于图象表征学生表现出3类错误，按其错误率进行综合分析，如图6．

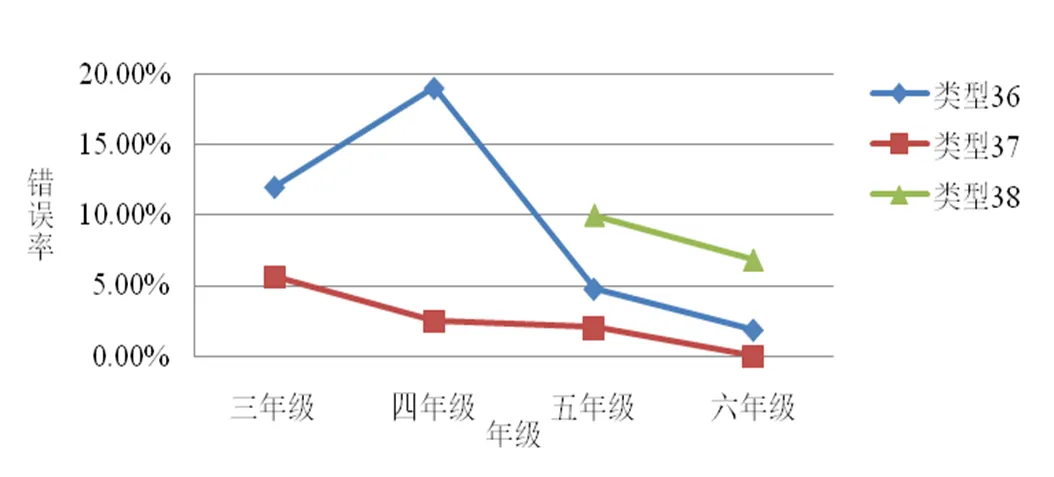
图6 “分数图象表征”概念不同错误类型错误率

分析可以得出以下结论．

（1）在这3类错误中，平均错误率由高到低依次为：类型36、类型38、类型37．

3.4 “分数比较”概念的错误类型及发展

分数比较，即分数大小比较．研究中不仅考查学生对分数大小的判断，还考查学生是否完全掌握分数大小比较的理论．由于分数的意义是“分数单位累加的结果”，对于从分数意义上来比较分数的大小，就是比较该分数包含的分数单位（当然，这里指相同的分数单位）的多少[15–16]．

类型41：概念不明确．例如，答案正确，理由不完全正确．

类型42：概念混淆．认为分子大的分数反而小，混淆了同分母分数比较大小和同分子分数比较大小．

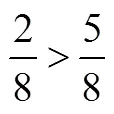
四–6：比较下列两个分数的大小，并在□里填写“>”、“<”或“=”．

四年级学生的错误率非常高，通过访谈了解到他们出现错误的原因是没有考虑单位转化．这些错误可以分为两种．

综上所述，对于分数比较概念学生会出现5类错误，按其错误率进行综合分析，如图7所示．

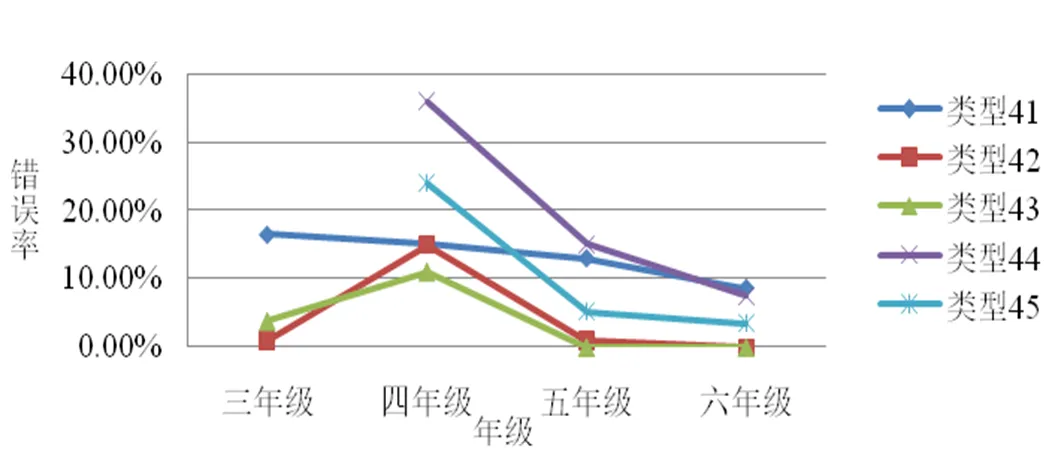
图7 “分数比较”概念不同错误类型的错误率

分析可以得出以下结论．

（1）在这5类错误中，类型41、类型44、类型45的平均错误率较高，其余类型错误率较低．

3.5 “等值分数”概念的错误类型及发展

等值分数是指在“整体1”相同的情况下，虽然两个分数所表示的份数不一样，但是所表示的大小是一样的．

四年级学生还没有学习“等值”这一概念，会出现以下3种错误：整数偏向错误、差值比较错误和加法错误．

整数偏向错误是指在进行分数比较时，将分子和分母看成两个整数，再进行整数间的比较．整数偏向错误分3种类型．

差值比较错误分两种类型．

加法错误是指学生将两个分数的分子与分子相加，分母与分母相加，得到两个分数的和．

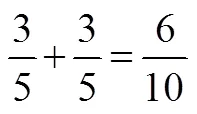
由于只有四年级学生才会表现出有关等值分数概念的错误，所以根据四年级学生的答题情况分析出6类错误的排序，如图8所示．

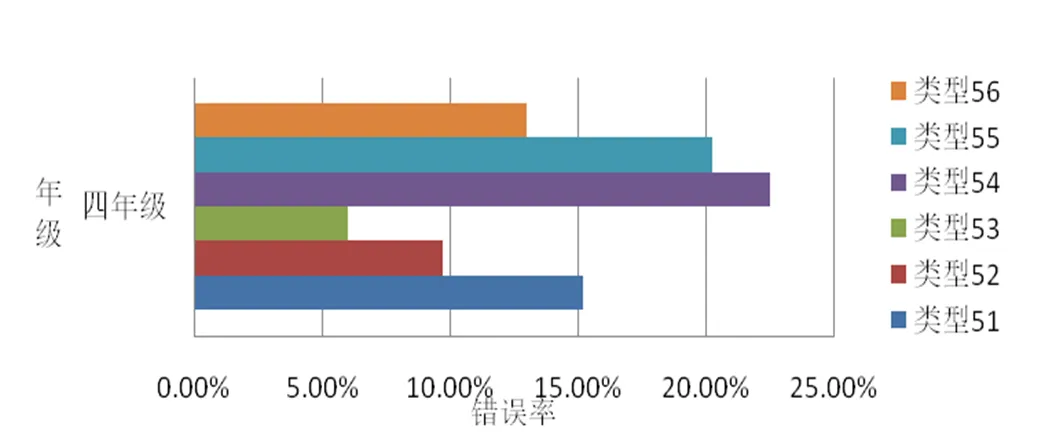
图8 “等值分数”概念不同错误类型的错误率

由图8可知，对于等值分数概念的6类错误来说，错误率由高到低分别为类型54、类型55、类型51、类型56、类型52和类型53．

3.6 “分数在数线上的表示”概念的错误类型及发展

分数在数线上的表示，即在数轴上标出分数．

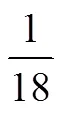
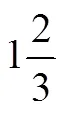
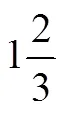
将上述3类错误进行综合分析，结果如图9所示．

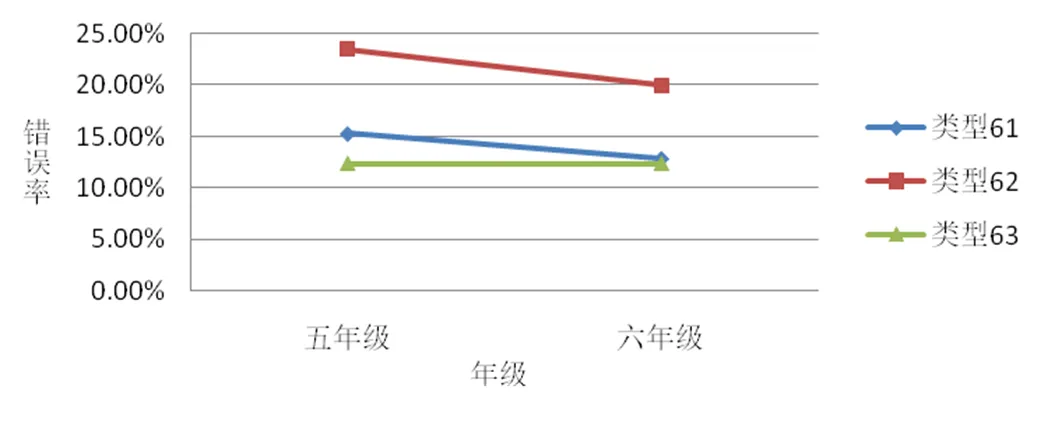
图9 “分数在数线上的表示”概念不同错误类型的错误率

分析可以得出以下结论．

（1）在这3类错误中，错误率由高到低依次为：类型62、类型61、类型63．

3.7 “分数与除法的联结”概念的错误类型及发展

分数与除法的联结是指将分数看作两个量相除的结果．

五–19：动物园里有7只大象，3只熊猫，熊猫的数量是大象的几分之几？请说明理由．

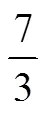
类型72：未理解分数与除法的关系．不能根据已知分数找到与之意义相同的除法表示．

综上所述，对于分数与除法的联结概念学生会出现两类错误，按其错误率进行综合分析，如图10所示．

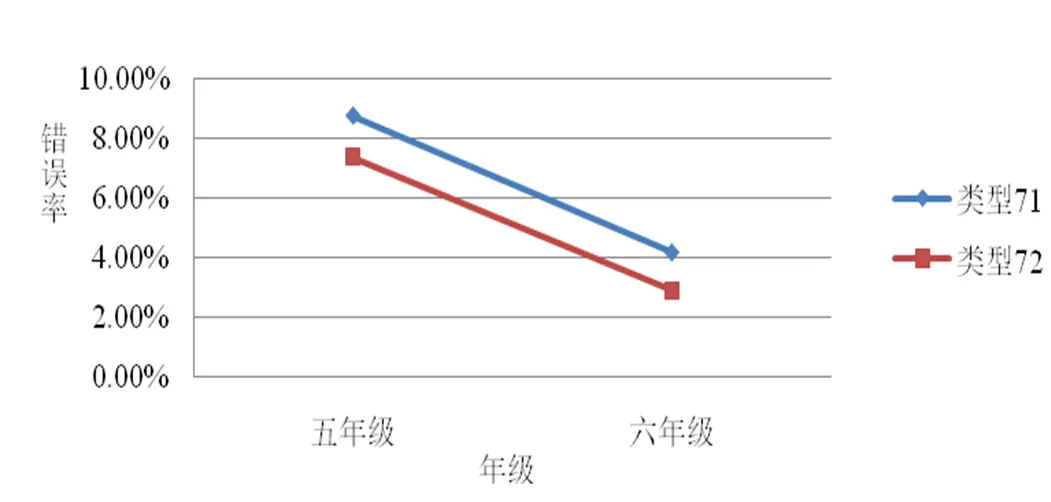
图10 “分数与除法的联结”概念不同错误类型的错误率

分析可以得出以下结论．

（1）在这两类错误中，类型71的错误率高于类型72．

4 结论与建议

4.1 结论

4.1.1 错误排序及发展

针对分数的7个子概念，选出错误率高于15%的主要错误，并按照平均错误率的高低排序如图11所示．

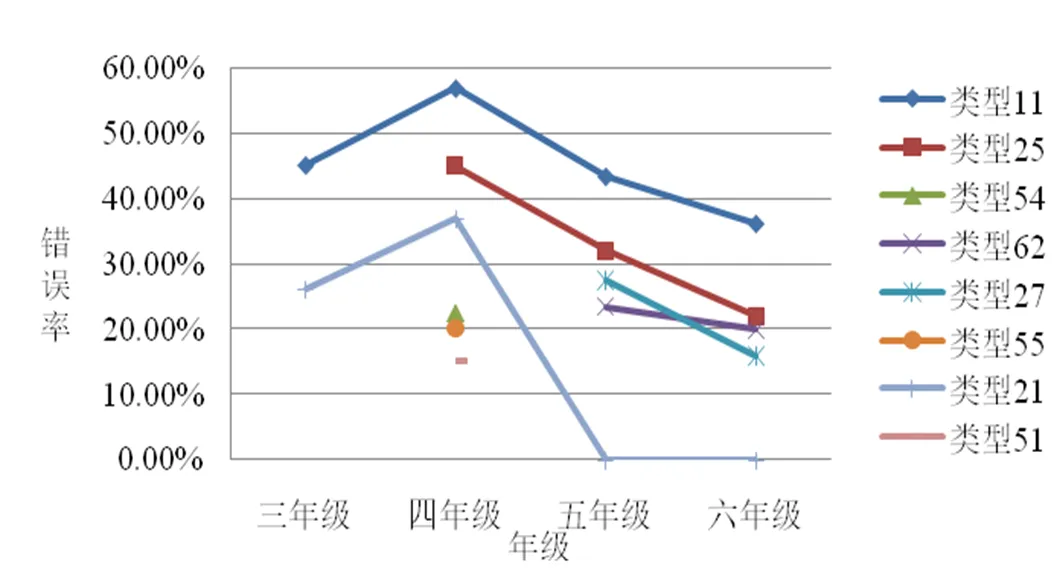
图11 错误率高于15%的主要错误

由图11可知，8类平均错误率高的错误中有6类错误（类型11、类型25、类型21、类型54、类型55和类型51）的错误率峰值出现在四年级，其中类型54、类型55和类型51仅在四年级出现．由于人教版小学数学教材仅在三年级上册、五年级下册和六年级上册涉及到分数知识，而四年级没有，时间跨度较大．这表明，对于学过的知识，如果教材不螺旋上升，学生可能会产生遗忘或建构偏差，从而影响后续学习．

此外，针对分数的7个子概念，先按照错误顽固与否，再按照错误率从高到底排序，发现三年级学习的4个分数子概念中存在12类顽固型错误（类型11、类型27、类型41、类型26、类型38、类型23、类型13、类型28、类型24、类型12、类型37和类型34），其中学习“单位量”概念时存在的顽固型错误最多，有5类（类型27、类型26、类型23、类型28和类型24）．

五年级学习的3个分数子概念中存在5类顽固型错误（类型62、类型61、类型63、类型71和类型72），其中学习“分数在数线上的表示”概念时存在的顽固型错误最多，有3类（类型62、类型61和类型63）．

三～六年级学生共存在5类非顽固型可消除错误（类型21、类型31、类型42、类型43和类型14）．

4.1.2 重要错误

关于分数7个子概念的8类主要错误详细信息如表1所示．

表1 8类主要错误

由表1可知，类型11、类型27、类型62是3类重要的错误．

4.2 建议

（1）在四年级加入适量分数内容，避免教材出现“空窗期”．

由于8类主要错误中的6类错误的错误率峰值均出现在四年级，而四年级又没有安排分数内容的学习，建议适当降低教材中分数知识的密集度．例如，将分数的单位量概念单独作为一块教学内容安排在四年级，让学生深刻体会单位量的意义以及分数单位的价值，这样既分散了难点，又加强了各部分分数知识之间的联系，避免分数知识的学习出现“空窗期”．五年级学生用分数表示部分与部分之间的关系与三年级学生的测试结果无显著性差异[16]，也正是“空窗期”所导致的．

（2）提高三年级“等分”概念、“单位量”概念和五年级“分数在数线上的表示”概念的教学比重．

在7个分数子概念的学习中，均存在顽固型错误，其中，三年级学习的4个分数子概念中，学生对于“等分”概念、“单位量”概念存在的顽固型错误最多；五年级学习的3个分数子概念中，学生对于“分数在数线上的表示”概念存在的顽固型错误最多．因此，建议教材提高三年级“等分”概念、“单位量”概念和五年级“分数在数线上的表示”概念的教学比重，帮助学生正确理解分数概念．

（3）教师应当根据学生的主要错误，有针对性地进行教学．

教师在进行分数知识的教学时，要把握分数知识的前后联系，结合学生的实际情况，合理安排教学内容，比如对于四年级学生出现的非顽固型不可消除错误、顽固型错误，在对五年级学生进行教学时，要格外关注；其次，根据学生学习分数概念时出现的8类主要错误，有针对性地进行教学与纠正．

5 不足与展望

受研究条件限制，调查对象为杭州市某小学的306名学生，整体而言，学生的水平相对农村学生而言，还是比较高的，这也导致了研究结果的代表性不足．问卷设计也是一件十分困难的事情，包含式问卷的好处是减轻了学生的测试负担，但问题也同时存在．

此外，该研究为横向调查，如果采用纵向追踪调查，可以更全面、真实地了解学生分数概念理解、发展历程，深入分析错误理解及其产生根源．

[1] 章勤琼，徐文彬．论小学数学中分数的多层级理解及其教学[J]．课程·教材·教法，2016，36（3）：43–49．

[2] 李健，郑莹．分数概念的演变及其教学启示[J]．内江师范学院学报，2018，33（12）：30–35．

[3] 吕玉琴．影响分数二分之一概念的因素[J]．国民教育，1993，8（5–6）：2–11．

[4] 李仙苹．小学五年级学生分数知识学习的错误类型之研究[D]．天津：天津师范大学，2012：39–56．

[5] 刘爱东．小学生分数概念典型错误及成因分析[J]．辽宁教育，2015，4（17）：89–92．

[6] 刘丹丹．小学六年级学生分数知识理解水平现状的调查研究[D]．长春：东北师范大学，2016：42–43．

[7] FIGUERAS O, FILLOY E, VOIDEUOROS M. Some difficulties which obscurethe appropriation of the fraction concept [R]. The 11th International Conference for the Psychology of Mathematics Education, 1987: 366–372.

[8] 刘春晖，辛自强．五—八年级学生分数概念的发展[J]．数学教育学报，2010，19（5）：59–63．

[9] STAFYLIDOU S, VOSNIADOU S. The development of students’ understanding of the numerical value of fractions [J]. Learning and Instruction, 2004, 14 (5): 508–518.

[10] BEHR M J, WACHSMUTH I, POST T R, et al. Order and equivalence of rational numbers: A clinical teaching experiment [J]. Journal for Research in Mathematics Education, 1984 (2): 33–40.

[11] MACK N K. Learning fractions with understanding: Building on informal knowledge [J]. Journal for Research in Mathematics Education, 1990 (21): 16–32.

[12] HUNTING R P. Rachel’s schemes for constructing fraction knowledge [J]. Educational Study in Mathematics, 1986, 2 (1): 49–86.

[13] 汤锦云．小学五年级学童分数概念与运算错误类型之研究[D]．屏东：屏东师范学院，2002：34–35．

[14] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：45–46．

[15] BRENNER M E, HERMAN S, HO H Z, et al. Cross-national comparison of representational conipetence [J]. Journal for Research in Mathematics Education, 1999, 30 (5): 541–547.

[16] BEHR M, POST T, LESH R. Representations in mathematics learning and problem solving [J]. Problems of Representation in the Teaching and Learning of Mathematics, 1987 (4): 323.

[17] 郭立军．整体把握与单元教学研究[M]．北京：北京师范大学出版社，2017：129–142．

Misconceptions and Development of Grades 3 to 6 Students on the Concepts of Fractions

GONG Zi-kun1, YANG Ting2, ZHANG Du3, ZHOU Xin-yi4

(1. Jing Hengyi School of Education, Hangzhou Normal University, Zhejiang Hangzhou 310012, China;2. Experimental School Affiliated to Zhejiang University of Technology, Zhejiang Hangzhou 310014, China;3. Xianlin Junior High School, Zhejiang Hangzhou 310000, China;4. Hangzhou Xinhua Experimental Primary School, Zhejiang Hangzhou 310015, China)

Based on the seven subconcepts of fractions, using four sets of inclusive questionnaires, 306 students in Grades 3 to 6 were selected to investigate types of misconceptions and development trends. It was found that the main mistakes were as follows: misunderstanding the concept of “equipartitioning,” misunderstanding the concept of “one whole” (including 3 subtypes), not using the number line to represent the fraction, and misunderstanding the concept of “equivalent fraction” (including 3 subtypes). The peak rate of 6 types of mistakes appeared in Grade 4, and the others appeared in Grade 5. Students made persistent mistakes in the seven subconcepts of fractions: Grade 4 students had the most mistakes on the concept of equipartitioning and Grade 5 students had the most mistakes on the one whole concept and the representation of fractions on the number line. We propose the following suggestions: Offer appropriate fraction content to fourth grade; provide more opportunities for students to learn the concepts of equipartitioning and one whole in the third grade and the expression of fractions on the number line in the fifth grade; and teachers should pay more attention to major mistakes.

students in Grade 3 to 6; cognition of fraction; misconception type

G622

A

1004–9894（2021）05–0014–07

巩子坤，杨婷，张都，等．三～六年级学生分数概念的错误理解及其发展[J]．数学教育学报，2021，30（5）：14-20．

2021–07–10

教育部人文社会科学研究规划基金项目——6～15岁儿童的概率概念认知策略及其发展研究（15YJA880020）；杭州师范大学省优势特色学科培育项目成果（18JYXK004）

巩子坤（1966—），男，山东滕州人，教授，主要从事数学核心概念认知与发展研究．

[责任编校：周学智、张楠]