数学合作问题解决视野下的“三教”探析

唐海军，严 虹，任 旭

数学合作问题解决视野下的“三教”探析

唐海军1，2，严 虹1，任 旭3

（1．贵州师范大学 数学科学学院，贵州 贵阳 550001；2．四川文理学院 数学学院，四川 达州 635000；3．国家统计局普查中心，北京 100826）

“教思考、教体验、教表达”（简称“三教”）作为在课堂教学中落实培养学生数学核心素养的重要途径，不但体现出21世纪教育变革的思想，也是培育满足21世纪技能需求人才的载体．从数学合作问题解决的视角，审视“合作问题解决”与“三教”的关系，着力分析了“三教”各个要素的内容、实践机会与策略以及评价标准，以期为中小学数学教师的教学实践提供一些理论指导与启示．

合作问题解决；教思考；教体验；教表达

近年来，越来越多的国家和教育系统重视以项目为基础和以探究为导向的学习[1]，都力图围绕批判性思维、问题解决（problem solving，简称PS）、自我管理和合作技能来塑造学校的课程和教学．基于项目的学习活动以合作解决问题的形式存在，通常包括需要多名学生一起合作，以实现完成团队任务的目标．由英特尔、微软等公司资助的美国21世纪技能的教学和评估项目（Assessment Teaching of 21st Century Skills，简称ATC21S）指出21世纪的核心技能包括批判性思维、问题解决、自我管理、信息和交流技术技能、沟通和合作[2]，它们都属于重要的软实力范畴．经济合作与发展组织（OECD）[3]也认为合作和沟通技能是未来人才技能体系的核心，所以由其发起的国际学生评估计划（PISA）在2015年的测评项目（PISA2015）中将合作+解决问题的能力作为测评参与国15岁中学生素养的重点内容之一．

“教思考、教体验、教表达”（以下简称“三教”）作为在课堂教学中落实培养学生核心素养的途径之一，已在贵州、重庆、四川等省市多所中小学校的数学、语文、物理等学科中实践运用，取得了一定的成果[4–11]．已有相关研究[12–15]表明，关键的教学行为、教学策略与学生核心素养的培养具有密切的关系．合作技能、问题解决技能作为重要的学习能力，它们与“三教”的关系有待揭示．同时，中小学教师在实践中也存在着，为什么需要“三教”，如何去设计与实施教学，如何检验“三教”实践的效果等疑惑．因此，研究者尝试从数学合作问题解决的视角，从理论上审视“合作问题解决”与“三教”的关系，着力分析“三教”的内容（是什么）、机会与策略（怎么做）、评价（做得如何），以期为致力于落实数学核心素养培养的教师、研究者等，在教学实践与研究方面有所启示．

1 内涵与关系

1.1 合作问题解决

ATC21S将批判性思维、问题解决能力、决策能力和合作能力综合为一个复杂的能力，即合作问题解决（collaborative problem solving，简称CPS）的能力．PISA2015正式提出：“合作问题解决（CPS）的能力是个体有效地参与两个或多个代理问题解决过程的能力，通过分享理解和共同努力达成解决方案，并结合知识、技能和努力来实现解决方案．”ATC21S的“合作解决问题的框架”认为CPS是一种多维度的技能，既包括社交技能，也包括认知技能，其中合作是主导链．社交技能包括：参与和合作、观点获取、社会调节；认知技能包括：任务管理、知识构建[16]．CPS能力的定义包含了3个维度的核心子能力：建立和保持共同的理解；采取适当的措施解决问题；建立和维护团队的行事规则．这3方面立足于团队合作与个人解决问题过程的有机结合．PISA关注点从问题解决（PS）转向合作问题解决（CPS），表明了对中学生学习的认识要从单一认知要素走向认知与社会互动的融合统一．

合作问题解决包括合作交流与问题解决两个部分，是宏观认知与群体沟通（macrocognition and group communica- tion）理论的应用．宏观认知侧重于不同背景和专业知识的人如何能够以某种方式与其他人互动，这种方式不仅允许共享表示，而且允许通过将先前获得的信息应用于新环境，形成新知识；群体沟通确定团体为完成特定的子目标（分析问题，确定问题困境、解决原理、解决结果）贡献时间和精力的程度，可以预测最终的效果．CPS的核心思想是社会共享认知[16]．合作交流体现了人类学习的社会属性，问题解决表现出人类学习的认知属性．维果茨基认为问题解决作为一种社会化过程，个人潜力可以通过与人类环境和各种工具的互动和相互支持的过程来实现．适当的人际交往活动可以促进个体的心理发展[16]．当试图通过思想交流来共同解决问题时，一群学习者建构出个人无法单独获得的共同意义．共同的意义只有通过群体内部的分享交流才能实现．维果茨基关于学习的社会文化性质的观点，引起了人们对能力更强的其他人（如监护人或同伴）可能在促进个别儿童学习方面发挥的作用的高度兴趣，同时也突出了知识和学习的文化历史背景．这种学习的社会文化观使研究人员注意到学习发生的情境的重要性[17]．也正因为如此，“情境认知”这一概念获得了教育界人士的普遍重视和广泛应用[18]．在情境学习理论中，巴拉布等认为教师应是学习和问题解决的专家，教师的工作是赋予学生真正的自主性，思维技能的指导，提供反思的机会，呈现结构不良的、真实的问题，以及合作性与社会性的任务等[18]．

1.2 “三教”的内涵

贵州师范大学吕传汉教授针对基础教育领域中存在重知识点、轻能力培养的应试化教学现状，结合国内外教育变革的背景，于2014年1月提出数学教学重在“教思考、教体验、教表达”的观点，认为“三教”是基于创新型人才培养，在学科教学中教学生积极思考、自主体验、善于表达，以此促进学生长见识、悟道理的一种教育理念．其后，在2015年10月又提出用“三教+”培育学生核心素养，尝试用“三教”引领数学“创设情境与提出问题”的教学，并将其推广到语文、英语、物理、化学等其它学科的教学中，其目的是用“三教”促进创新型人才的成长；用“三教”促进学生软能力增长，为国家培养第三产业发展需要的人才．

从宏观看，“三教”是一种教育理念，包含着教思考、教体验与教表达3个组成要素．教师通过“教思考”促进学生获得内在的认知与情感体验，在体验中通过讨论、交流、辩论、倾听、叙述、描写等方式，实现“教表达”；通过“教体验”引发学生新的思考，夯实问题表达的基础，实现将“教思考”获得的显性知识内化成隐性知识；通过“教表达”促成学生将学习活动中的体验外显化，并进一步在体验、表达的过程中，发现新的问题，开启新的思考．因此，“教思考”“教体验”“教表达”3者之间形成一种互为基础、相互依存的关系[4]．

从微观看，“三教”又是一种培育学生数学核心素养的途径．教体验，让学生会用数学的眼光观察世界，注重数学抽象和直观想象核心素养的培养．诱导学生在学习中不断发现问题、提出问题、分析问题和解决问题．教思考，让学生会用数学的思维分析世界，注重逻辑推理和数学运算核心素养的培养．在不同阶段，引导学生在“做数学”中，发展、积淀个性化的素养，让全体学生都得到相应的发展．教表达，让学生会用数学的语言表达世界，注重数学建模和数据分析核心素养的培养．鼓励学生叙述参与数学活动的思维过程，发表对数学问题的理解与看法，提出数学学习中的疑难与困惑并交流数学学习的体验与感悟．

1.3 合作问题解决与“三教”的关系

1.3.1 数学合作问题解决孕育着“三教”

（1）合作问题解决中的“思考”．

数学合作问题解决（CPS）的有效性既依赖于团队成员合作的能力，又取决于成员视团队的成功优先于个体的成功的理念．CPS本质上仍然是一种问题解决的能力，要保证小组在解决问题方面因协助的产出大于单个成员的产出的总和[19]，部分参与者的个体数学水平，虽然可以低于其他成员，但是不能完全依赖于他人的协助而放弃自身的努力．也就是说数学问题的高效解决也取决于团队成员要始终保持对数学问题的情境特征与问题解决过程（如问题表征、模式识别、解题迁移、解题监控）的高水平思考．美国科学院发布的《2025年的数学科学》报告指出，学生在学会处理那些并没有精确陈述的问题时，将接触各种各样的数学和统计思考模式（关键的数学知识、建模与仿真、算法、概率方法和统计推断），并获益匪浅．Leone Burton认为在数学问题解决的过程中进行数学思考包括了4个核心阶段[20]：第一是特殊化，指的是遇到一个相对复杂的问题，要先研究该问题的诸多具体情况，目的是便于理解和讲解，进而寻求解决问题的一般规律；第二是猜想，通过诸多具体问题的解决，发现他们之间的联系，总结出一般性的结论和规律，这种未经证明的结论或规律即称为猜想；第三是一般化，在问题解决之后，把相应的结论或方法推广到更为广泛的范围，这种过程就是一般化；第四是确认，一般性的结论需要得到认可，在数学中也称为证明．在问题解决的过程中，学习者既要思考，更能促进其深度思考．

（2）合作问题解决中的“体验”．

数学合作问题解决（CPS）的过程既涉及个体单独解决问题的认知过程，它同时又涉及认知和社交技能，即与其他参与者的认知系统交互的交流过程．这一过程，既有个体内在的对数学学习的体验，又有因观点分享而获得茅塞顿开的惊喜．对于学生而言，“如果要认识数学在世界中的作用，他们必须具有在各种问题情境下解决现实世界问题的丰富经验”[21]，通过与成员比较和对比具体事例，以拥有思考数学的应用价值，体验数学的美学价值．Mogens Niss教授认为应用数学的目的有3个方面[22]：为了理解（表征、解释、预测）部分世界；为了用各种行动（包括制定决策、解决问题）掌控部分世界；为了设计数学之外的世界（创建或塑造人造事物，即对象、系统、结构）．当学生在合作解决数学问题，用数学的思维分析世界，用逻辑推理和数学运算处理问题，从而经历有用的数学学习之旅时，上述目的，不但为学生指明了数学学习的意义，也为教师的教学提供了准绳．教师在问题解决前后，通过询问学生“当我们从多角度看待现实世界问题时，数学有什么用？”来评估学生通过解决一系列任务后真实的数学学习体验；通过问题解决前后感受的对比还可以估计学生对数学应用的欣赏．问题解决中体验的积淀，必然促进学习者素养的增强．

（3）合作问题解决中的“表达”．

数学合作问题解决（CPS）所涉及的认知行为既是认知主体对数学问题的加工、内化，又表现为与群体其他人的互动．Brennan研究表明成功的问题解决需要问题表达和符号运算能力，数学问题解决也是一个对数学语言阅读、理解、转译、加工和表达的过程[23]．CPS的前提是团队成员努力建立并保持对任务及其解决方案的共同理解，这种理解是成员通过交流和互动所构建的一个共同点[24]，具体表现在共享问题意义的表示，理解成员的角色、能力和观点，相互传递信息和跟进反馈，并相互监控解决方案的进展．总之，要实现对数学问题的完全而正确理解，学生对数学准确的表达是达成信息充分交流的关键．数学语言是数学表达的基础，数学交流是数学表达的目的．在问题解决团队中的表达，必然激起成员之间的思维碰撞：在表达中倾听，在倾听中交流，在交流中深度思考，促进学习者对知识学习的理解、增长智慧、积淀素养．

1.3.2 “三教”是“合作问题解决”融入教学的途径

从合作问题解决走向“三教”，既是从一般问题（社会或生活）转向到学科问题，又是从课外问题解决转移到课堂数学教学．因而，最核心的还是要回归到对数学教学本质的认识．

关于如何教数学，Kuhs和Ball（1986）提出了3类教学观[25–26]：以内容为中心并强调任务绩效的工具主义；以任务为中心并强调概念性理解的柏拉图主义；以学习者为中心的问题解决（社会建构主义）．以学习者为中心的教师认为数学学习是在学习团体中构建知识的一个积极过程[25]．问题解决的教学观关注学习者对数学知识的构建，重视学习者的主动性、学习环境的社会性，认为学习不仅是个体对学习内容的主动加工，而且需要学习者进行合作互助；认为不同文化、不同环境下个体的学习和问题解决之间存在着很大的不同．这种教学观是情境认知理论与建构主义发展的结果，突出问题解决是认知、社会、文化等情境因素的交融，这与合作问题解决的主张相吻合．心理学家江绍伦认为教学还是一个涉及教师与学生在理性与情绪两方面动态的人际交往过程；是一个与个性及社会心理现象相联系的情感力量和认知力量相互作用的动力过程[27]．由此，合作问题解决教和学的过程至少涉及到认知、社会和情感3个相关维度的动态交互．

David Clarke认为人类想要达成共识或主体间性（共享理解）的自然倾向，是学生在课堂合作环境中进行意义协商的一种源动力[17]．合作的环境包括内容框架和关系空间，它们存在着认知（人际）冲突、观点协商与形成共识，其中在内容框架中通过对数学问题解决的尝试和思想观点的思考、质疑、评价等，获得对任务所涉及的数学知识更深入的理解；在关系空间中，小组成员具有实质性的互动（如，体验、坚持、妥协等）有助于建立共同的理解，推动问题解决任务的完成；话语的表达交流是衔接内容框架与关系空间的中介．由此，教师经历“情境设计—教学干预—成果评价”的流程，情境设计为学生提供活动的载体，教学干预保障交流持续有序进行，成果评价反馈进一步促进全班学生达成共识．

心理语言学家Herbert H. Clark的共同点（common ground）理论[16]认为作为解决问题的参与者必须具有某种共享（同）知识才能解决任务，话语沟通是构建共享理解的主要手段．在实践中，学生参与合作解决数学问题的积极思考是形成共享知识的前提，在自主尝试过程中拥有对问题基本信息的共同认知；善于表达是做到共享表示的基础，在合作交流中归纳出小组对某个观点、解法或模型的共同表示；自主体验是达成共享理解的内在要求，在组内、组间、师生、生班等多元的分享反馈，以及显性与隐性知识之间的转化扩散中，完成问题的共同理解．因此，学生在教师所创设的问题情境下，课堂合作问题解决学习经历一个“自主尝试—合作交流—分享反馈”的过程．

CPS教学中认知、社会和情感三维度与思考、表达和体验，既是相互对应，又是不可分割的整体．合作问题解决是“三教”理念的源泉之一，“三教”是保障合作问题解决能够融入教学、落地生根的途径．由此，概括出合作问题解决与“三教”关系模型（如图1）．要实现CPS的教学从理念走入课堂，从CPS视角探索“三教”的实践（内容、策略、评价），遂将变得必要．

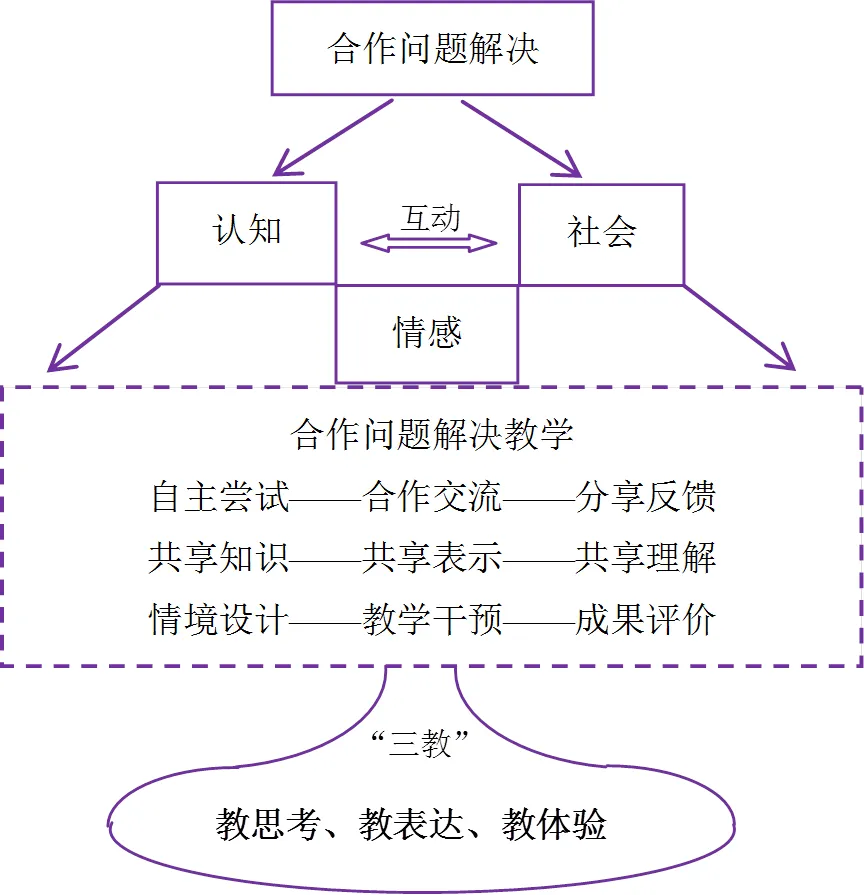
图1 “合作问题解决”与“三教”关系

2 CPS视角下的“三教”实践探索

2.1 教思考的有效实践

2.1.1 数学思考的内容

思考也是思虑，是思维的一种探索活动，源于主体对意向信息的加工．合作问题解决过程中，需要思考什么？

思考数学问题的情境特征与类别．在PISA2012数学框架[28]中所定义的4种情境类别（个人、职业、社会、科学）有助于澄清何时、何地、为谁而设置问题情境．从4种不同类别的情境思考教学，可以帮助教师均衡地使用不同的问题情境[21]．学生通过思考问题的情境有助于解读问题的已知信息、隐藏信息以及找到与已有认知的联系．

思考数学问题解决的策略．解决问题的策略从形式上大致分为具体策略，半具体、半抽象策略和抽象策略．从心理学上又分为算法（algorithm）和启发法．算法通常指固定的程式、规则和步骤，通过固有的算法学生能够获得问题的解，如中小学数学课堂中求解常规问题．启发法又分为“手段—目的”分析法（如类比、归纳，通过设置子任务来缩小原目标与初始条件的差距）、“逆向综合法”（即通常说的由结论逆推到初始条件）、简化建模法（提取问题的主要结构，如数量关系、图形要素位置关系，再建立模型，做到从简入繁）．

思考数学问题解决的过程．Leone Burton所主张的在数学问题解决的过程中数学思考的4阶段：特殊化、猜想、一般化和证明是处理问题的一种范式，但操作具有局限性，特别是针对学困生而言．参考PISA2012的问题解决过程：“探究和理解、表达和构思、计划和执行、监控和反思”，可以认为数学问题解决采用“观察（条件）—联想（已知）—转化（未知）—反思（监控）”更有利于学生解决数学课堂中结构良好的问题．

2.1.2 数学思考的机会与策略

（1）思考机会的充分性．

对于如何教思考，已有研究[5]从课程设计、创造性思考技巧、情意培养营造等方面有详细的介绍，还有一大批中小学教师立足于一线教学论述了中小学数学教学实践中如何落实“教思考”，在此不再赘述．其实，目前中小学数学课堂最为缺少的是学生拥有对问题解决的思考机会．在课堂观摩中，常常发现教师剥夺了学生思考的权力，教学处处在为完成既定的教学目标让路与服务．

课堂需要思考的时机，提倡为学生“让学”的慢教育理念．“让学”是指在某一时段老师安排学生进行自主学习的课堂行为[29]．“让学”源于德国哲学家马丁·海德格尔（Martin Heidegger，1889—1976）的教学理念，与国内新课程倡导的“生本”教学理念有异曲同工之妙．

（2）思考策略的多元性．

教思考的重心是引导学生形成良好的数学思维．联合国教科文组织在《学会生存》一书中指出：“教师的职责现在已经越来越少地传授知识，而是更多地引导、激励思考．”引导学生对问题解决全程进行分析和思考，采用综合、分析、类比、迁移、联想、想象等思维活动，触发灵感，引发领会、理解，继而解决问题，实现激思、会思、善思的目的[29]．

教思考的切入点是引导学生养成反思质疑的习惯．“反思”是数学教学中应该特别倡导的批判性思维方式[4]．反思是元认知（反审认知）活动，是对思维过程的审视，是完整的思维过程的重要组成部分．（例如，学生在问题解决时，看问题的角度是否最佳？分析过程的逻辑关联度如何？问题解决的情感态度是积极还是消极？）质疑既体现了思维的灵活性和深刻性，更体现了思维的主动性．“质疑是一种能力，对于学生而言更是一种品质——主动思考的意识、独立判断的意愿、不断探究的精神．”反思质疑不是胡乱猜测、故意刁难，而是获得更有效的、遵循数学知识生成规律的思考．教学中向问题解决小组提供挑战性的数学认知学习任务，组织学生经历一次数学学习的“再创造”过程，来加强学生数学反思能力的培养[30]．

教思考的关键是设计数学核心问题作为思考的载体．核心问题是基于核心知识和学生认知水平，关注核心素养培育，统领课堂教学的情境性问题．核心问题为学生提供合适的数学思考基点，“以核心问题为统领，以问题串为线索，促进学生在数学学习过程中更为积极地思考”[6]，发展学生的数学抽象、逻辑推理等核心素养．这关键又在于教师在分析教材时要有整体的问题意识，要厘清单元核心问题、课时核心问题，保障合作问题解决能够围绕教学重点、持续、有效地进行．

（3）思考内容的有序性．

由于物质的系统结构或运动是确定的、有规则的，那么，有序是指根据事物的结构形式或系统组成诸要素之间的相互联系，找出动态变化的规律．面对一个问题情境，教师示范或者引导学生按一定的顺序与步骤，采取相应策略来解决问题，就呈现出思考问题的有序性．这既是发展学生数学逻辑推理素养的策略，也是课程标准的要求．在数学教学中，教师可以通过“动手实践、类比迁移、比较应用、跟进追问等不同的策略积极引导学生进行有序地数学思考，帮助学生掌握数学思考的一些基本方法”[31]．具体而言，立足于数学教材与学生思维的特征，通过具体表象，循序渐进，逐渐抽象等步骤，培养学生能做到有根据有条理地发现问题、提出问题、分析问题和解决问题．

2.1.3 数学思考的有效测评

如何测评数学思考的深度，涉及测评教师“教思考”的实践与学生“数学思考”的水平两个方面．文[5]建议从潜阶段、萌芽阶段、充分表现、杰出表现等4个阶段的行为表现来描述、诊断数学教育中的“教思考”水平差异．这样的阶段划分与行为标准的科学性还有待实验验证．思考是一类深刻、周到的思维活动．如何测评学生在问题解决过程中的思考？并尝试对思考进行等级的划分．不妨尝试从无效的思考与有效思考两个维度来测评学生数学思考的深度．“有效的数学思考是指能够运用数学的思维方式进行比较深刻、周到的数学思维活动，并达到了预期的数学思考目标，获得了预期的学习效果．”[30]有效的数学思考呈现出逻辑性、自控性、反省性、层次性等基本特征．

2.2 教体验的有效实践

2.2.1 数学体验的阶段

基于体验的学习方法认为学习者获得技能和构建知识是体验的直接结果．根据Newsome、Wardlow和Johnson[32]的体验学习方法提高了学生的认知水平，增加了批判性思维技能的使用，提升了学生获得、保留和检索知识的能力．体验学习可以在没有老师的情况下存在，并且只与个人直接体验的意义形成过程相关．那么，数学学习需要经历的体验过程是什么？从美国凯斯西储大学的组织行为学教授David Kolb所开发的体验学习模型（图2）来看，学习的过程被分为具体经验、观察反思、抽象概括和尝试应用等4个循环往复的环节[33]，所有这些阶段都是学习必须经历的．

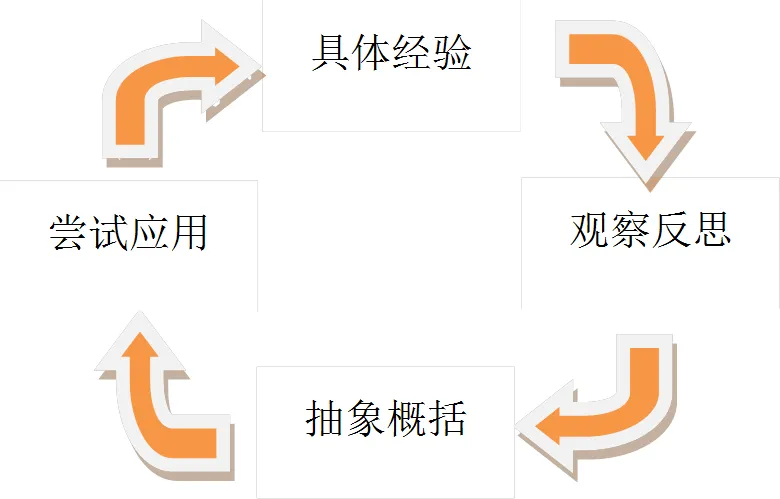
图2 David Kolb的体验学习模式

在Kolb的体验式学习循环中，具体经验阶段，学习者参与团队问题解决的过程．教师的角色是描述学生工作时的活动表现．观察反思阶段，学习者通过与以往经验的观察比较，反思问题解决的方法、团队分工与过程，取得学习的新想法．教师的作用是设计活动，帮助学习者通过具有批判性的数学眼光来建构意义和思考自己．抽象概括阶段，要求学习者运用逻辑和系统的方法，进行抽象符号的思维操作，以使概念更趋向于简洁和精确，提出问题解决方案．尝试应用阶段，学习者使用他们在抽象概括阶段得到的结论来预测现实世界，能够在新的情境下运用或检验结论和方案的普适性[34]．他们的行为是一种新的体验．

该学习模式强调通过具体体验得到的经验是学习的核心，并且经验可以进一步检验学习者自身所概括的概念和结论；学习过程是以反馈为基础与目标，指导下一步行为，为学习结果评价提供了依据[35]．

2.2.2 体验的机会与策略

（1）体验机会的充分性．

数学学习，学生要能够获得体验，教师首先要在教学设计与实施中努力创设体验的机会，摒弃“工具主义与柏拉图主义”的教学观．主体获得亲身经历和感受的途径主要有直接感知、参与活动和生活积累[36]．感知、活动、生活是形成体验的3种直接途径，教师的“教体验”则需要在这些方面着力，通过创设合作问题解决的平台，预留交流互动的时间，给予抽象对象直观感知的机会．教师提供问题解决经验的指导是学生在数学学习时也能够如艺术课程一样，经历一个活跃的、丰富的、深刻的内心活动过程的保障．

（2）体验策略的多样性．

数学体验是学生素质形成与发展的核心环节．索云旺等认为，学生数学体验生成、获得的教学策略主要有：营造开放的课堂教学环境，让学生对学习活动产生强烈体验的内驱力；创设良好的数学问题情境，唤起学生的情感活动，使学生获得发现和提出问题的数学体验；让学生经历“再创造与再发现的过程”，获得科学发现的体验；倡导学生积极主动地参与“数学建模”活动，鼓励学生在数学体验中主动成长[37]．陈秀春通过3年（2003—2006）的教学实验研究归纳出数学体验教学模式是[38]：启思探索—反思创新—辨析拓展—反刍体验，并在“知识产生的背景—知识形成—思想方法发展、观念升华—数学应用”的教学内容中实施．通过对初二学生的检测，发现实验对学生的数学观有明显改善，对学业成绩及数学的创造性思维都产生了积极影响．

（3）体验内容的真实性．

从心理学上来讲，“体验是在对事物的真切感受和深刻理解的基础上对事物产生情感并生成意义的活动”[36]，故而要强调数学学习体验内容的真实性．其一，避免空洞的感悟，数学虽然是抽象与理性思考的结果，但数学并不等于抽象．体验是联系主体内心世界与外在客体的纽带，既有直接运用多种感官去接触事物，对事物形成鲜活、具体、深刻、丰富的印象和感受，又有间接通过文字阅读、抽象反思、拓广应用等方式来实现主体对客体的内化．其二，由于体验是从对事物的感受开始形成的，因此，对于抽象思维能力较弱与问题解决经验还不够丰富的中小学生而言，数学问题解决的亲身经历和直接经验对于数学体验的形成具有特殊的意义．今天，在沉浸式艺术领域，艺术家借助科学技术手段（3D虚拟、全息影像）将人们的视、听、触、嗅各个感官融合起来，引导人们参与、交互到抽象艺术形成的过程，达到化抽象为直观的艺术体验效果．随着，教育信息技术的发展，数学学习领域的体验，也能如艺术一样，在某些方面做到远离虚无、体验有物．其三，体验的真实性，须防止因“教体验”而忽略认知结果，误入“为体验而体验”的歧途．教师要从淡化形式，重视过程与结果，关注学生积极的情感体验等角度来杜绝形式主义的假体验．

2.2.3 数学体验的有效测评

在Kolb看来，体验既可以是客观具体（具体体验）的，也可以是主观抽象（抽象概括）的．具体体验架起了社会知识向个人知识转化的桥梁，体验学习在重视具体体验或直接经验的同时，并没有否认抽象概括或间接经验在个体学习和发展中的重要性，因而对体验的测评要从整体、递进和连续的维度来进行．

若按照大脑在接受信息时所依赖的感觉种类的等级差别，把学生学习的体验从具体到抽象分为6个水平[39]：第一水平是“身临其境”的亲身体验；第二水平是“沉浸”体验；第三水平是真实的“动手”体验；第四水平是替代性的“动手”体验；第五水平是对真实影像、模型的体验；第六水平是对抽象符号的体验．体验是一种操作抽象与心理感知相融合的复杂性活动，以短暂的行为、情绪表现出来，影响着对事物认知与情感的判断．对其测评实属不易，该标准是否能够实现对学生数学问题解决的体验的准确测评，还有待进一步的实证研究．

2.3 教表达的有效实践

2.3.1 数学表达的途径

在数学合作问题解决过程中，教师教学生表达的方式是什么？不妨从表达的主要途径入手来进行划分．

“读数学”，指学生阅读出问题情境中的数学概念、符号、公理和定理等内容的活动．通过“读”来实现学生主动与数学文本、知识、问题的直接对话，“促进学生展开想象，数学文字生成数学图形，促进学生理解与掌握抽象的数字知识”[40]．

“说数学”，是指个体用口头向成员或自我表达对数学问题的具体认识、理解，解决问题的思路以及数学学习情感、体会等的数学学习活动．它还涉及“说知识”“说过程”“说异见”“说体会”[41]．

“写数学”，指用笔在纸上书写或电子产品上输出数学符号、文字或图形的活动．问题解决中自己写草稿、记讨论笔记、写成果报告、板书解题步骤、发布数学公告等都是写数学的内容．书写“既是学生巩固数学知识、提升计算能力、优化问题解决策略的有效手段，也是展现团队合作过程、反馈学习信息的重要途径”[40]．

“画数学”，指的是以绘制图形、图象来反映数学问题空间各要素关系的活动．例如新加坡的漫画数学，国内小学教育近年兴起的绘本数学、思维导图等都力图借助画或描绘的方式，将抽象与枯燥的数学概念、公式渗入数学活动、故事情境中，通过可视化手段变得易于认识、理解与交流．

2.3.2 表达的时机与策略

（1）表达时机的充分性．

数学课堂中，充足的表达时间、公平的表达机会，是目前中小学数学课堂最为缺少的一环．由于课时的限制，教师不敢过多地放手学生阐述问题、交流信息或者仅供少数“学优生”展示数学成果，同时因为教师自身对表达重要性认识不到位，导致教学设计中以封闭性问题居多，学生难以有参与表达的机会．Frendenthal（1973）指出教师的主要目标是为学生创造有意义的学习情境，然后将其引入数学表达，这些问题情境为学生提供数学化经验和建构数学知识的机会．Louise Wilkinson主张[42]：教学生表达首先就在于鼓励教师创造情境与设计任务，把基本的数学知识和技能嵌入到教学任务中，并指导学生使用正确而规范的数学表达．当学生不能恰当地进行数学表达时，教师应该寻找适当时机，用数学术语重述（recast）他们的解决方案．

（2）表达形式的多样化．

“读、说、写、画”是数学表达的常见形式，除此之外，教师还需要从语言学的多模态话语理论来认识数学多元表达的重要性[43]．多模态话语指运用听觉、视觉、触觉等多种感觉，通过语言、图像、声音、动作等多种手段和符号资源进行交际的现象．多模态话语的媒体系统包括语言与非语言媒体两部分，随着多媒体话语的产生，人们直到最近几年才逐步认识到其重要性，将其作为一个独立的学术领域进行研究，并指导应用于外语语言学习领域．随着“教育信息化2.0行动计划”的推进，智慧教育已经从技术开发走入课堂实践，再结合多模态话语的媒体系统可知，今天的数学的表达远不止平时课堂上“读一读、说一说、写一写”这样粗略．除传统的数学表达形式之外，教师也要有意识地思考非传统表达形式对数学学习的辅助作用，并应用于教学实践．

（3）表达内容的教育化．

社会文化理论家提出，学生在课堂上理解和使用特定的话语形式是社会化的．Wertsch认为，课堂话语至少包含：日常生活中的语境化话语和学术领域中使用的特殊语言形式[44]．过多的日常生活中的话语难免导致数学语言缺乏的纯粹性与严密性，毕竟“专业表述能力是学生学科素养的重要标志”[45]，而单纯的数学专业语言（如标准的数学概念术语、公式符号）又将导致学生难以理解数学、走进数学，甚至视数学为异类而产生厌学情绪，所以在代数领域根据数学语言类型与特点，采用自然引入符号语言、分析数学句法特点、调整语句顺序，……，适度通俗化等方式，把数学语言的学术形态转化为教育形态[46]．

在几何证明领域，日本福井大学柳本成一教授开展了数学表达教学改革实验．首先把学生带入几何思维的世界（对几何图形“先记号化、再符号化”的数学表达）；然后引导学生运用几何逻辑推理的规范形式表达数学思维过程；最后，根据不同几何思维形式（类型1：扩展已知图形；类型2：换元已有关系得出新条件；类型3：分解已知图形解决中间问题；类型4：组合部分图形解决问题），运用相应的数学方法的逻辑来求证命题[47]．这项研究得到了日本文部科学省持续20年的科研经费资助．

总之，教师在指导中小学生进行数学合作问题解决时，数学表达上既要避免过多的“口语化”（直观但不严谨），又要谨防太过专业的“数学化”（标准但妨碍理解）．用教育形态的数学教学语言深入浅出地表述数学问题，揭示数学思维特征，既通俗易懂又不失“数学味”．

2.3.3 数学表达的有效测评

数学学习是复杂的，需要学生和教师去认识和使用各种类型的知识，包括用语言和非语言的方式来表现数学思想[48]．如何测评数学问题解决过程中数学表达的水平，同样包含教师指导学生时教表达的水平与学生通过数学学习后数学表达的水平．数学也许比任何其它学科更重要的是，知识的构建取决于教师的口头语言解释和互动．Veel指出，在数学课上，教师口语占主导地位，需要教师的话语来解释视觉和符号表征构成的含义．教科书提供的解释往往是专业而精简的，因此教师在帮助学生学习符号、图表和技术语言方面起着关键作用[49]．对师生而言，侧重于从表达时间的充分性、时机公平与恰当、话语的准确性、话语内容（管理性话语、教（学）内容话语、策略性话语、元认知话语、综合性话语）的层次性、表达的多模态等角度来构建数学有效表达的标准，并进行测评．如何更科学地测评数学表达的水平，也是今后值得进一步研究与实践的问题．

3 结语与展望

3.1 “三教”与数学合作问题解决相辅相成

“三教”与合作问题解决关系密切．教思考核心在于培养学生的问题意识，触发新的问题生成，反之，问题又激活学生对相关知识的深度思考；教体验核心在于引导学生参与问题解决过程，夯实个人对数学新知建构的经验积累与内心感悟，反之，问题解决给予学生体验数学的契机；教表达核心在于促使学生在问题解决中将个人对数学问题的理解和解题的策略通过准确、生动、形象的数学语言展示给团队成员，与他们进行成功地对话、接受其他成员的评判，为实现达成维护团队共同理解的目标做出贡献，反之，合作的问题解决又为数学表达能力的培养提供了载体．

Dillenbourg和Traum指出，从人类在合作学习环境中的相互作用中获得的一些经验证据表明，成员间的持续交流可能比共同的外在呈现更能促进群体的“共同化”，从而支持参与者产生“最佳协作的努力”，获得足够的学习和绩效[16]．那么，合作问题解决若要走进数学课堂教学，并实现学生认知“共同化”的目标，关键在于“三教”内容设计、干预策略和成果评价要确保学生能做到可持续交流．

3.2 “三教”的研究问题还有待继续拓展与深化

自2014年以来，贵州师范大学“三教”研究团队带领中小学数学专家团队，陆续在贵州、四川、重庆等省市的部分中小学校开展“三教”+“情境问题”教学实验，以此为抓手来推动培养学生数学核心素养，确保课程改革的理念能够落实于课堂．实验开展过程中，也发现尚有很多概念需要澄清、疑问亟待解决，例如，（1）“三教”对教师的核心能力（学科素养）有什么要求？（如，教师是否自己能够认识到问题解决中需要思考什么，体验什么．）（2）“三教”的3个要素所对应的“教与学”如何评价更为科学？已有测评原则或标准是否科学，还有待实证研究．（3）中小学具有考试、升学压力的背景下，数学课堂何以保障学生的思考、体验与表达？（4）不同学科“教思考、教体验、教表达”如何与相应学科的核心素养培养相衔接，教学实施中与数学学科有何异同等．

[1] National Research Counci. A framework for K-12 science education: Practices, crosscutting concepts, and core ideas [M]. Washington, DC: The National Academies Press, 2011: 1–3.

[2] BINKLEY M. Defining 21st century skills [M] // GRIFFIN P, MCGAW B, CARE E. Assessment and teaching of 21st century skills. Heidelberg: Springer, 2011: 17–23.

[3] OECD. The OECD guide to measuring the information society 2011 [M]. Paris: OECD Publishing, 2011: 12–17.

[4] 严虹，游泰杰，吕传汉．对数学教学中“教思考、教体验、教表达”的认识与思考[J]．数学教育学报，2017，26（5）：26–30．

[5] 王宽明，吕传汉，游泰杰．对数学教育中“教思考”的探索[J]．中小学教师培训，2018（3）：39–43．

[6] 严虹，游泰杰，吕传汉．“三教”引领中小学数学教学培育核心素养探究[M]．贵阳：贵州人民出版社，2018：213．

[7] 张晓斌，付大平．落实“三教”理念，培育数学核心素养[J]．中小学教师培训，2017（8）：54–57．

[8] 谢学智．“三教”引领乡村中学数学教学培育核心素养课例选编[M]．贵阳：贵州人民出版社，2018：3–17．

[9] 任旭，夏小刚．职前数学教师数据分析教学的认知发展研究——基于贵州地方高师院校的调查与分析[J]．数学教育学报，2018，27（6）：82–87．

[10] 严虹．连贯性视阈下“代数思维”课程设置的比较研究——以“中”“美”“英”“澳”“新”“南非”六国课程内容为例[J]．数学教育学报，2018，27（6）：60–66．

[11] 严虹．德育内容视域下中小学理科课程标准的文本研究[J]．教育理论与实践，2021，41（8）：44–49．

[12] 曹一鸣，于国文．中学数学课堂教学行为关键性层级研究[J]．数学教育学报，2017，26（1）：1–6．

[13] 曹一鸣，李信巧，郭转娜，等．初中数学教师非正式交流研究——基于中国3个地区七年级数学教师的调查分析[J]．数学教育学报，2021，30（3）：12–17．

[14] 郭衎，曹一鸣．知识与信念：基于学生表现的教师核心素养研究[J]．数学教育学报，2021，30（4）：1–5．

[15] 唐海军，高晶．初中数学教科书中历史名题分布特征及启示[J]．数学教育学报，2020，29（5）：8–13，102．

[16] OECD. PISA 2015 collaborative problem‑solving framework [M] // PISA 2015 assessment and analytical framework: Science, reading, mathematic, financial literacy and collaborative problem solving. Paris: OECD Publishing, 2017: 161–163.

[17] CHAN M C E, CLARKE D. Dialogue and shared cognition: Student-student talk during collaborative problem solving [C] // GRAVEN M, VENKAT H, ESSIEN A, et al. Proceedings of the 43rd conference of the international group for the psychology of mathematics education. Pretoria, South Africa: PME, 2019: 145–152.

[18] 郑毓信．数学哲学与数学教育哲学[M]．南京：江苏教育出版社，2007：377，381–382．

[19] SCHWARTZ, DANIEL L. The emergence of abstract representations in dyad problem solving [J]. Journal of the Learning Sciences, 1995, 4 (3): 321–354.

[20] BURTON L. Mathematical thinking: The struggle for meaning [J]. Journal for Research in Mathematics Education, 1984, 15 (1): 35–49.

[21] 凯·斯泰西，罗斯·特纳．数学素养的测评——走进PISA测试[M]．曹一鸣，译．北京：教育科学出版社，2017：237–238．

[22] NISS M. Perspectives on the balance between applications and modeling and “pure” mathematics in the teaching and learning of mathematics [C] // MENGHINI M, FURINGHETTI F, GIACARDI L, et al. The first century of the international commission on mathematical instruction (1908—2008). Roma: Enciclopedia Italiana, 2008: 69–84.

[23] 刘喆．小学生数学表述状况调查及数学表述教学模式研究[J]．数学教育学报，2011，20（1）：26–30．

[24] CLARK H H, BRENNAN S E. Grounding in communication [C] // RESNICK L B, LEVINE J M, TEASLEY S D. Perspectives on socially shared cognition. Washington, DC: American Psychological Association, 1991: 127–149.

[25] VOSS T, KLEICKMANN T, KUNTER M, et al. Mathematics’ beliefs [M] // KUNTER M, BAUMERT J, BLUM W, et al. Teachers’ professional competence: Findings of the COACTIV Research Program. New York: Springer, 2013: 249–271.

[26] 陈倩，梁贯成．课程改革背景下中国教师的数学信念[M] // 范良火，黄毅英，蔡金法，等．华人如何教数学．南京：江苏凤凰教育出版社，2017：403．

[27] 涂荣豹．数学教学认识论[M]．南京：南京师范大学出版社，2004：253．

[28] OECD. PISA 2012 assessment and analytical framework: Mathematics, reading, science, problem solving and financial literacy [M]. Paris: OECD Publications, 2013: 23.

[29] 华云锋．“让学引思”：初中数学课堂的新视点[J]．教学与管理，2017（2）：62–64．

[30] 邓友祥．有效数学思考的内涵与特征及教学策略[J]．数学通报，2013，52（2）：7–10．

[31] 张海生．促进学生“有序思考”的教学策略[J]．教育理论与实践，2015，35（20）：53–55．

[32] NEWSOME L A, WARDLOW G W, JOHNSON D M. Effects of lecture versus experiential teaching method on cognitive achievement retention and attitudes among high school agriscience students [C] // National AAAE Research Conference, 2005: 146–156.

[33] KOLB D A. Experiential learning: Experience as a source of learning and development [M]. New Jersey: Prentice-Hall, 1984: xiii, 256.

[34] CHESIMET M, GITHUA B, NG’ENO J K. Effects of experiential learning approach on students’ mathematical creativity among secondary school students of Kericho east sub-county, Kenya [J]. Journal of Education and Practice, 2016 (7): 51–57.

[35] 大卫·库伯．体验学习——让体验成为学习和发展的源泉[M]．上海：华东师范大学出版社，2008：18．

[36] 陈佑清．体验及其生成[J]．教育研究与实验，2002（2）：11–16．

[37] 索云旺，童嘉森，吴万辉，等．论数学体验及其生成[J]．数学教育学报，2004，13（1）：75–78．

[38] 陈秀春．体验式教学模式的实践与思考[J]．中学数学教学，2003（5）：18–19．

[39] 石雷山，王灿明．大卫·库伯的体验学习[J]．教育理论与实践，2009，29（10）：49–50．

[40] 杨晓翔．“读听写说”在中学数学教学中的应用[J]．数学通报，2013，52（4）：21–24．

[41] 钟进均．基于语言学视角的“说数学”探究[J]．数学通报，2013，52（3）：11–14．

[42] 赵凌云，李沐慧，路易丝· 威尔金森．数学学习中“数学表达”的前沿研究——路易丝· 威尔金森（Louise Wilkinson）与赵凌云、李沐慧的对话[J]．华东师范大学学报（教育科学版），2018（6）：144–149．

[43] 张德禄．多模态话语分析综合理论框架探索[J]．中国外语，2009，6（1）：24–30．

[44] ELLICE A, FORMAN, DAWN E M, et al. Learning what counts as a mathematical explanation [J]. Linguistics and Education, 1997, 9 (4): 313–339.

[45] 郑泽芝．关于学科教材语言研究问题的思考——以数学教材语言研究为例[J]．北华大学学报（社会科学版），2017，18（6）：1–6．

[46] 吴宝莹．从数学语言的学术形态到教育形态[J]．教学月刊（中学版），2013（4）：49–53．

[47] 刘京莉．学会用数学语言表达几何逻辑思维过程[J]．数学通报，2007，46（5）：30–32．

[48] WILKINSON L C. Teaching the language of mathematics: What the research tells us teachers need to know and do [J]. Journal of Mathematical Behavior, 2018 (5): 1–8.

[49] VEEL R. Language, knowledge and authority in school mathematics [M] // CHRISTIE F. Pedagogy and the shaping of consciousness: Linguistic and social processes. London: Continuum, 1999: 185–216.

Research on the “Three Teachings” Theory from the Perspective of Mathematical Collaborative Problem Solving

TANG Hai-jun1, 2, YAN Hong1, REN Xu3

(1. School of Mathematical Science, Guizhou Normal University, Guizhou Guiyang 550001, China;2. College of Mathematical Sichuan University of Arts and Science, Sichuan Dazhou 635000, China;3. Census Center of National Bureau of Statistics, Beijing 100826, China)

“Teaching thinking, Teaching experience, Teaching communication” (abbreviated as the “Three Teachings”) is an important way to cultivate students’ core math competencies in the classroom. It not only embodies the idea of educational reform but is also the catalyst for cultivating talented students who meet the needs of the 21st century. From the perspective of mathematical collaborative problem solving, this study examines the relationship between collaborative problem solving and the three teachings and focuses on the analysis of the content, opportunity, strategy, and evaluation of each element of the three teachings. The study has implications for guiding elementary school teachers’ teaching.

collaborative problem solving; teaching thinking; teaching experience; teaching expression

G420

A

1004–9894（2021）05–0072–08

唐海军，严虹，任旭．数学合作问题解决视野下的“三教”探析[J]．数学教育学报，2021，30（5）：72-79．

2021–08–25

全国教育科学“十三五”规划一般项目——中学生合作问题解决中认知互动与社会互动及其关系的实证研究（BHA180157）；贵州师范大学2018年度研究生创新基金资助项目——初中生数学课堂合作问题解决中的教师干预研究（YC[2018]035）；2021年度四川省高校人文社会科学重点研究基地——四川教师专业发展研究中心《基于学生作业的实习教师教学反思与教学重建研究》（PDTR2021-08）

唐海军（1982—），男，四川南充人，讲师，博士生，主要从事数学教学、教材分析与数学文化研究．

[责任编校：周学智、陈隽]