小学数学教学中数学推理的理论和实践

张侨平，邢佳立，金轩竹

小学数学教学中数学推理的理论和实践

张侨平1，邢佳立2，金轩竹3

（1．香港教育大学 数学与资讯科技学系，香港 999077；2．浙江外国语学院浙江教学月刊社，浙江 杭州 311002；3．珠海华发教育发展有限公司，广东 珠海 519060）

数学推理是数学学习的核心，然而对推理的定义和数学推理的形式有许多不同的看法．首先分析了理解数学推理的4种不同视角，涵盖结果视角、过程视角、结构视角、模仿与创造视角．在此基础上，以小学阶段代数、比例和空间3个内容为例，对数学推理能力在其中的具体体现和相关的推理教学进行了分析．教师可通过在教学中设计创造性的推理任务以及鼓励学生解释与表达等方式促进数学推理在课堂教学中的落实．

数学推理；数学学习；小学数学教学

1 问题提出

让学生懂得数学推理和具备数学推理的能力是学校数学教育的重要目标之一．在国际学生能力评估计划（Programme for International Students Assessment，简称PISA）2021数学能力框架中，数学推理被视作学生数学素养的重要组成部分[1]．早在1950年中国第一份小学算术课程暂行标准中，就提出要“训练儿童善于运用思考、推理、分析、综合和钻研问题的方法和习惯”[2]，21世纪初中国启动的课程改革不仅将培养学生的数学推理能力视为数学教育的重要目标，而且对其表现形式进行了更为清晰的描述[3]．在新近颁布的高中数学课程标准中，明确将逻辑推理作为学生需要具备的重要数学核心素养之一[4]．而在新近提出的中国学生发展核心素养中，“逻辑清晰，思维缜密，能多角度、辩证地分析问题，做出选择和决定”一起被看作“科学精神”这一核心素养的重要表现[5]．由此可见，重视学生的推理能力并不只是局限于数学教育，它在整个学校教育中都发挥着至关重要的作用．

值得注意的是，当大家在谈论推理时，好像彼此之间都清楚推理这个概念指代的是什么，但实际情况却并非如此．因为不同学者对数学推理的理解存在相当大的差异[6]，在不同学习阶段以何种方式进行推理的教学也会有不同的看法，例如，数学推理和一般推理的关系是什么？如果学生尝试对一列数字的变化规律进行总结但并没有成功，是否属于推理活动？让学生根据例题解决同类型的新问题能看作是培养他们的推理能力吗？如果把这类问题的争论聚焦在数学教学，也就是该怎样理解数学推理以及如何进行推理教学．如何认识和理解数学推理，如何培养学生数学推理能力，如何将数学推理教学渗透在课程学习领域是研究者着重探讨的地方．

2 理解数学推理

2.1 什么是推理

推理是人们学习和生活中经常使用的思维方式，也是数学的基本思维方式．不同学者对推理有不同的看法，总的来说，推理与论证、推断、思考有紧密的联系但又有不同．这里借鉴哲学家图尔明（Toulmin）与教育心理学家莫什曼（Moshman）的观点，来辨析这些与推理相似的概念，希望能为广大研究者理解课堂中的推理教学，特别是数学推理提供一些参照．

图尔明认为推理的重要特点在于其社会性．具体而言，个体本身及其所处环境的差异会造成观点与判断标准的不同，某一群体中“不证自明”的观点并非适用于另一个群体，而推理便是人们在交流中为支持与维护某个主张而批判地检验与筛选观点的过程．这一过程是具有集体性质的、持续不断的协商过程（human transaction）[7]．图尔明着重分析推理和论证之间的关系，他认为论证（argumentation）可被视为一系列的推理（trains of reasoning），它们构成具体表述内容的一连串相互关联的主张和理由，包含主张或结论（claim）、数据或资料（data）以及理由或论据（warrant）3个基本成分[8]（如图1所示）．图尔明关于推理的定义主要强调个人在推理活动中所处的情境和人际间的互动，注重考虑逻辑结构的完整性和正确性，对学科知识的正确性涉及较少，其论证模式常常被用作分析学生论证的评价标准．

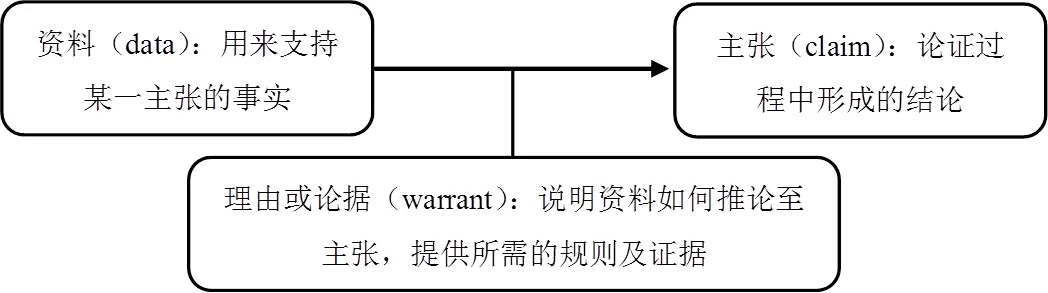
图1 图尔明的论证模式

教育心理学家莫什曼则从认知心理学的视角对发展推理所需要的能力进行探讨，他认为推断（inference）和思考（thinking）是推理能力发展的前提[9]．推断是最为基本与普遍的行为之一，例如婴儿时期根据声音推断物体的位置、从成人的面部表情推断其情感，在日常的对话、阅读等活动中都离不开推断．思考则是有意识、有目的地运用推断解决问题、做出决定、判断与计划等，是个体认识与控制自己认知过程的能力，即原认知能力（metacognition）的体现．在具备推断与思考能力的基础上，个体进行推理还要能够将推论与意图同适当的推论准则相结合，莫什曼称之为知识认知（epistemic cognition）[9]．认知心理学视角对推理的理解，凸显个体的认知能力，以及程序与规则在推理中的必要性．

以上从哲学和心理学层面关于推理的分析，指出了推理的内涵和特点．这些观点既重视推理的主要成分和逻辑结构，也强调个体在推理活动中的心理历程．课堂教学是涉及人的活动，师生与学生间互动和交流是培养推理的重要方面，它不仅仅是具有个人特质的行为，更是由一系列集体性的实践和准则所构成的活动．因此，数学课堂中进行推理的教学，需要了解推理中涉及与学科知识相关的主张或结论、资料，以及理由或论据，在关注学生个体的心理历程前提下，多鼓励学生进行推断和思考，同时也考虑推理过程中逻辑结构的完整性和正确性．下面结合数学学科的具体内容分析数学推理的特点．

2.2 理解数学推理的4种视角

在现有关于数学推理的研究中，存在多种类别的划分方式，而不同类别与表述的背后所反映出来的实际是研究者对数学推理不同方面的关注．例如，在课堂教学中应将推理视为数学学习结果还是学习过程本身？推理教学应着重于不同推理结构的理解，还是关注推理策略得到的方式？下面将结合前文中提出的逻辑结构与心理特征两个方面对数学推理的界定从4个不同的视角进行分析和总结．

视角1：结果（product）视角，这一视角更关注推理中的逻辑结构，着重推理所产出的结果，将推理视为在任务解决过程中形成主张并得出结论的一系列想法，强调推理所产生的新知识与新成果[10]．这种看法并非否定推理的过程性，更多是出于对观察与分析便利的考虑，从结果的视角来定义数学推理，看重学生思考分析、解决问题的结果．

视角2：过程（process）视角，这一视角在关注逻辑结构的同时也关注个体在推理过程中的心理特征，侧重于指明推理的对象或推理所需要的环节．从这一视角出发的学者比较多，如汤普森（Thompson），他提出数学推理包括对量和结构进行的有目的推论、演绎、归纳[11]；史宁中认为数学推理的思维过程和逻辑性体现在所涉及命题内涵之间的传递性[12]，而“经历和感悟了数学归纳推理和演绎推理后积淀的思维模式”即为数学的基本活动经验[13]．另外，珍妮特（Jeannotte）与基兰（Kieran）从社会文化视角出发，结合推理过程中的认知与沟通，将数学推理界定为通过与自我对话或与他人进行对话，从一个数学观点推断出另一个数学观点的过程．在文献分析基础上，他们提炼出3个主要类别（寻找相同与差异、证实和例证）共9种数学推理的过程[14]．例如，寻找相同与差异的过程可分为概括、猜想、识别规律、对比和分类；证实的过程则包括证实、验证、证明（不一定要演绎的方式）和正式的证明（主要是演绎推理）．由于例证是通过提供具体的事例来支持推理，既可以被用于寻找异同，也可以作为证实过程的支持，因此在两个类别之外单独呈现．个体的思维活动是极为复杂的．这些不同类别的推理活动并非是完全独立或依序发生的，各个过程之间是相互关联、促进与影响的．例如，在对数学对象的属性和定义进行分类时，个体无疑需要经历比较、假设以及概括等环节而寻找异同点．总之，对推理过程的关注与剖析在揭示推理复杂性的同时，也为课堂教学中促进学生推理提供了可能的路径，教师可据此设计相关任务与活动，推动学生进行推理．

视角3：结构性视角，侧重在推理中如何从主张走向结论，着重描述构成推理逻辑结构的各个要素及其相互关系，据此也有公认的3种推理形式，它们是演绎（deductive）推理、归纳（inductive）推理和溯因（abductive）推理．演绎推理和归纳推理是较为熟悉的类型．中国《义务教育数学课程标准（2011年版）》将数学推理是划分为合情推理和演绎推理．合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等手段推断某些结果；演绎推理是从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算[3]．最新修订的《普通高中课程标准》中进一步指出，逻辑推理主要包括两类：一类是从特殊到一般的推理，推理形式主要有归纳、类比；一类是从一般到特殊的推理，推理形式主要有演绎[4]．演绎推理被视为唯一一类能够得到确定结论的推理，也是数学教学中常常涉及的一种推理形式．而归纳推理在实践中更多表现为对规律的找寻，通过猜想、寻找模式等提出一个具有一般性的结果．

相对合情推理和演绎推理来说，溯因推理被提及得并不多．哲学家皮尔逊（Peirce）最早把溯因法引入现代逻辑用以区别演绎与归纳推理．一般来说，溯因推理是从已有事实出发构建推理的过程，即解释已知事物的过程[15]．例如，通过“三角形内角和是180的倍数”这一法则，以及“900是180的倍数，而870不是”这一事实，来解释“为何七边形的内角和应为900，而非870”，便是溯因推理的体现．为区分3种不同的推理形式，皮尔逊借助实例（case）、法则（rules）和结果（results）这3个要素对不同形式的推理进行了描述[16]．其中，实例是指一定条件下（如某一事物的特点或两个事物间的联系）的具体观察；法则是指“一种情况发生，那么另一种情况同样出现”的命题；结论虽然同例子有一些相似，但其中蕴含了规则．在数学学科，里德（Reid）结合数学学科的内容对这三要素进行了解释与补充，应用于数学推理中[17]．图2提供了一个关于直角三角形的例子．法则是演绎推理的核心，实例是归纳推理的基础，而溯因推理的目的则是为了借助法则与结果解释当下的实例．康纳（Conner）等人进一步尝试将上述数学推理的三要素与图尔明的一般论证模型结合起来，更加直观地呈现在不同类型推理中，各个部分间的相互关系，较为清晰地展现了实例、法则和结果在不同推理类型中所扮演的角色，帮助学生有机会经历与体验不同的推理过程[18]．

图2 结构视角下不同数学推理的表现形式

视角4：模仿和创造性推理．较之前3种视角，利特纳（Lithner）提出的模仿推理（imitative reasoning）与创造性推理（creative reasoning）更加聚焦于推理策略得到的方式（如图3所示）[19]，也就是更关注推理中个体经历的心理过程．模仿推理是指通过回想或效仿某些既定程序而进行的机械推理，主要包括记忆推理（memorised reasoning）和算法推理（algorithmic reasoning）两类．当学生进行记忆推理时，问题解决策略的选择是基于对一个完整答案的回忆，而策略的实施仅仅是将回忆出的答案抄写下来．此类推理在数学教学中也十分常见：学生将背诵的证明或解题步骤套用于新问题中；也会因“之前的题目有（没有）这样的答案”等理由而选择（拒绝）某种作法．

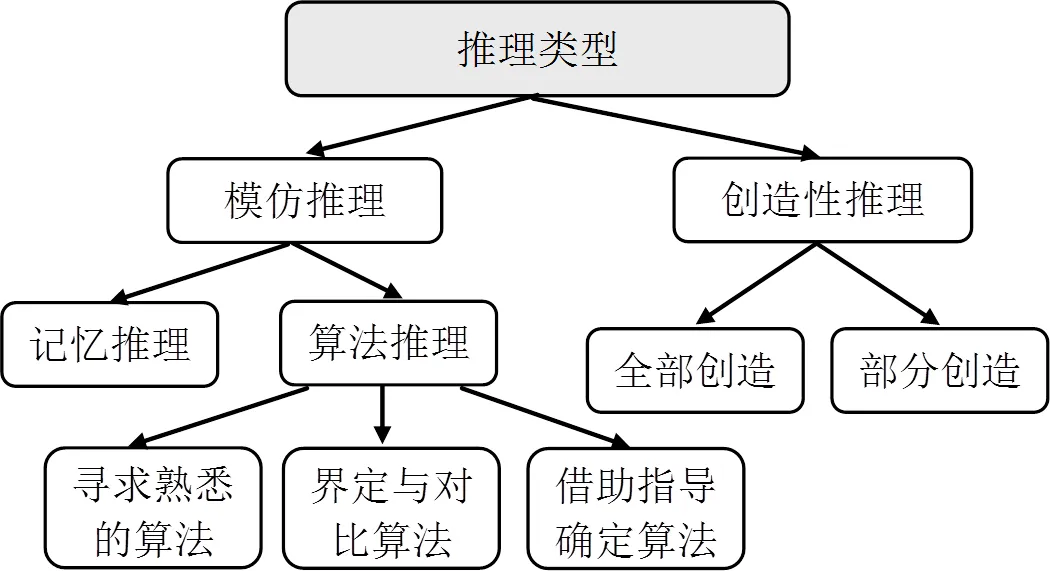
图3 模仿推理和创造性推理的划分

模仿推理中另一类是算法推理，这里的算法并非仅指计算中的步骤或方法，而是泛指一切预先制定的程序．学生在进行算法推理时，会对全部已知的策略进行筛选，在预测不同策略的可能结果后作出选择，策略的实施等其余推理环节对于推理者则不太重要，除非由于粗心所造成的计算错误，否则一定会得到正确答案．换而言之，识别与选择合适的程序是算法推理中的关键与主要任务．

创造性推理在数学学习中并不少见，其推理过程多会涉及到模仿推理．例如，学生在解决某些图形面积问题时可能就需要运用背诵的长方形面积公式等．根据所包含模仿推理的多少，可将创造性推理分为全部创造与局部创造，即使是局部创造也包含着创新的成分．这里的创造并不是那些天才的发明，而是一些新的策略与方法，包括重新再创造出已经遗忘的策略．利特纳提出了创造性推理的3个基本标准[19]：

●新颖性（novelty）：即对于推理者而言是全新的推理序列，或者重新创建一个被遗忘的推理序列；

● 合理性（plausibility）：策略的选择、实施与结论的得出都有一定论据的支撑；

● 数学基础（mathematical foundation）：相关论点、论据的提出皆符合数学的性质与属性．

不同于传统的演绎推理和归纳推理划分，着重于推理逻辑结构的各个要素及其相互关系，利特纳所提出的推理类型更关注学生个体在推理中的心理历程，为理解数学推理提供了新的视角，特别是帮助理解学生数学问题解决的过程，比如透过分析学生的推理过程，可以知道学生在问题解决过程中的策略和答案究竟是来源于对问题内容的分析、比较等，还是仅仅是基于回忆与猜测．

总的来说，尽管研究中存在对数学推理的不同理解，但还是脱离不开图尔明提到的推理结构中的各个要素及其相互关系．不同视角下的推理类型只是更强调这一逻辑结构的某些部分，这些不同的理解会有助于研究者从不同角度培养学生的数学推理能力．例如，重视过程视角的数学推理促使教师关注推理所包含的具体环节，重视结构视角的数学推理为教师设计与选择教学任务提供依据，重视模仿与创造性推理，则能帮助教师对教学活动中学生的数学推理进行诊断和分析．

3 小学数学教学中数学推理的体现

从理论层面对推理的概念进行分析后，不难发现，数学推理作为一种思维方式贯穿于数学学习活动的全过程．因此，教师并非只有在特定的数学内容或特定的教学环节才适合培养学生的数学推理能力．不过也应看到，对于不同的学习内容，数学推理的表现形式确有不同．故此，结合国内外的相关研究，对学校数学教学中的代数推理、比例推理和空间推理3种常见的数学推理的特点进行介绍，并结合具体的例子为教师如何进行数学推理教学提供参考．

3.1 代数推理（algebraic reasoning）

代数推理被视为学生在数学与科学方面取得进步的“守门人（gatekeeper）”[20]．代数推理往往涉及到对数学结构的探索，而这是进行一切数学思考的基础[21]，而且代数推理也渗透于日常生活的方方面面，诸如购物中对商品的比较，驾车时对行驶时间的估计，等等．另外，从小学数学学习到中学的一个明显转变就是正式开始代数学习，这一转换对于大多数学生而言往往是十分困难的．研究表明，在小学阶段有意识地培养学生代数推理能力能够为学生实现这一转换提供相应的支持[22]．代数推理可以视作是对具体的数字与计算进行概括，将所得到的结论用有意义的数学符号进行表达，并对所得到的模式进行探索．简而言之，寻找（looking for）、识别（recognizing）、概括（generalizing）与运用（using）潜在的数学结构（mathematical structures）构成了代数推理的几个重要方面．其中，数学结构既可以指代广义的群、环、域等课题，也包括由具体运算所抽象出的结构、规则和一般化的算理等．这里主要基于后者对数学结构的定义对小学阶段的代数推理进行分析．

小学阶段的代数推理主要体现在理解符号的意义与数字的不同属性，明晰加减乘除运算中的算理等．代数推理的核心是用符号表示出概括的结构，但在正式的学习中，代数通常是以预定的规则语法和符号语言呈现，供学生记忆，学生几乎没有对符号意义及其规则进行探索与表达的机会．那么要如何渗透代数推理？举例来说，在早期数学学习中，教师可采用实物或鼓励学生使用自己“创造”的非正式符号表示算术属性，如“★+ ★= 2 × ★”，并对其中的关系进行陈述与解释．同样，教师也可通过引导学生考虑奇数、偶数不同组合相加后所得结果的奇偶性，以促使学生从关注“和”的多少，到对“和”的不同属性进行代数思考．类似的例子还包括探索加法交换律与乘法交换律等．学生在这一过程中进行猜想、比较与归纳等，在形成意义理解的同时也提高升了推理能力．

再如教学8的乘法口诀，如果只是简单引入口诀，然后请学生通过背的方式记忆口诀再应用到问题解决中，那么学生就只是在应用简单的模仿推理．而如果将教学的过程丰富起来，引导学生思考并交流讨论，提出诸如“八八六十四”这句口诀是怎么来的这样的问题，学生就可能提出：（1）8×4=32（4个8相加），那么8×8=64（8个8相加，就是4个8相加的翻倍）；（2）8×3=24（3个8相加），8×5=40（5个8相加），合起来就是8×8=64（8个8相加）等不同的思路，如果从过程的角度来看待这段教学，学生就是在经历“通过与自我对话或与他人进行对话，而从一个数学观点推断出另一个数学观点的过程”，这一过程中恰恰可以体现学生对内容的“比较与分析”，创造性地解决问题．

此外，“找规律”的形数问题也是代数领域推理能力的体现．小学阶段可通过提供有一定规律的视觉图片为学生提供探索与建立数量间的关系的机会．例如，图4左边是一种重复变化模式，为低年级学生创造了一种简单的递归模式，体验初步的模式分析与预测的推理过程；图4右边则属增长变化模式，可以用以引导学生从关注“每次增加2浅灰色砖”的数量变化到提炼出图形序号同砖块数之间的关系，并对任何序号下的砖块数量进行预测[21]．这一过程也能为将来中学阶段的函数思想的形成奠定基础．

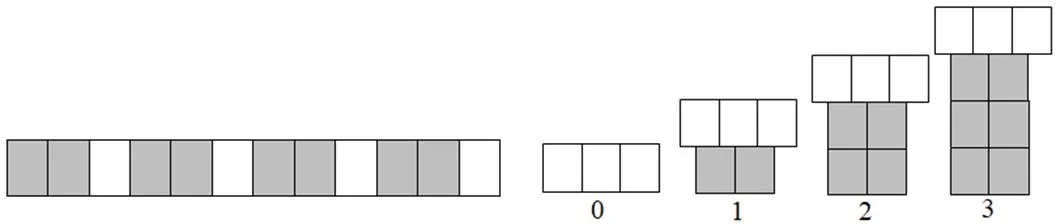
图4 培养函数思想的代数推理任务

除了上述方法外，在具体数字运算中进行发现、总结、理解与应用算理也是进行代数推理的重要方面．较之加法与乘法计算，一些研究者更倾向于使用“加法推理（additive reasoning）”和“乘法推理（multiplicative reasoning）”以凸显其中所涉及的对数字的拆分组合．例如，斯特弗（Steffe）认为，加法推理需要学生能够将数字视为复合单位的概念（composite unit），从而根据要求进行拆分与组合[23]，比如从推理的角度讲，期待学生不但能够计算“7+4=？”，还要能够在“7+4=？”和“11–7=？”之间进行灵活转换．在此基础上，祖尔（Tzur）提出乘法推理与加法推理的差别在于学生需要进一步对复合单位进行协同操作，即将其中一个复合单位分配到另一个复合单位之中，并通过协同计数得到总数[24]．这样看来，即便是理解“在3个篮子中每个都放入两个苹果，共有多少个苹果”这样的问题，实际也需要学生进行如下的推理：1（篮子）—2（苹果）、2（篮子）—4（苹果）、3（篮子）—6（苹果）．

3.2 比例推理（proportional reasoning）

将比例推理单独罗列而没有归入代数推理，主要考虑是因为理解与解决比例问题不单单是运用符号或是进行乘法运算，而是要基于具体情境把握其中的关系变化．正如皮亚杰（Piaget）所说，比例推理的特点之一在于其并不是简单地讨论两个量之间的关系，而是对两对关系（second-order relationship）进行描述、预测以及评估[3]．这也是比例问题的难点所在，学生必须要从惯用的加法推理以及绝对变化观念转变至乘法推理和相对变化观念．比例推理结构的划分见图5．

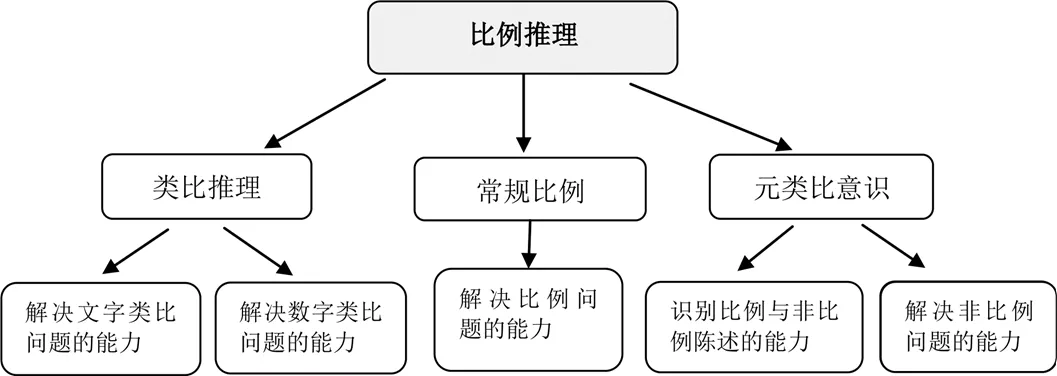
图5 比例推理结构的划分

比例推理在小学阶段主要涉及：（1）义务教育阶段第二学段数与代数领域中的“正比例、反比例”，这部分内容要求学生能够理解实际情境中比及按比例分配的含义，并解决简单问题；在具体情境中认识成比例的量和成反比例的量；画出正比例关系图并会根据其中一个量的值估计另一个量的值；以及能够找出生活中成正比例和反比例的量并进行交流．（2）数与代数领域中数的运算部分中，“路程=速度×时间”也涉及比例关系的理解与建构．

在许多研究以及教科书设计中，利用比例关系计算出缺失量（missing-value）被视为比例推理能力的体现[25]．例如，回答一些类似“制作3杯浓缩果汁需要6勺苹果汁和12杯水，那么制作6杯浓缩果汁需要几勺苹果汁”的问题．但比例推理所涉及的方面远不止此．莫德斯托（Modestou）和加加希思（Gagatsis）认为，比例推理能力除表现为解决常规的比例推理任务外，还应包括类比推理和原类比意识两个方面．由此所建构的比例推理模型也为研究者理解与培养比例推理提供相应的参照[26]．其中，类比推理是指个体识别与运用文字与数字中所包含的模式的能力，相关问题包括同义词（聪明 vs 聪慧）、分类（画作与艺术 vs 语言和文学）、关系配对（钢笔和墨水 vs 颜料和画笔）等文字题目，以及整数比：如，6∶3=8∶___（2，4，16）；非整数比：6∶4=9∶___（1，3，6）；平方关系：6∶36=8∶___（37，64，72）等数字类比问题．

类比推理作为一种特殊的推理，适用于培养低年级学生初步体验依据关系进行推理的过程，为后续比例能力的发展奠定基础．元类比意识则主要是指通过对给定情境进行分析，以识别与判断是否存在比例关系．对情境进行分析与判断既是比例的重要特点，也是开展比例推理的前提与基础．典型的情境判断问题有：“如果一名9岁的小男孩高1.23米，那么在他18岁生日时，他的身高将达到2.46米”和“小明今年8岁，爸爸32岁，当小明10岁时，爸爸是40岁”．比例始终是数学学习中的难点之一，从小学阶段有意识地帮助学生体验变化关系，辨析问题情境能够有助于学生后续的学习．

3.3 空间推理（spatial reasoning）

空间推理可以被定义为受试者由空间对象或表征建造心像并进行操弄，以进行空间表征间变换的认知历程[27]．中国义务教育课程标准提出从实物与图形的转换、物体的位置、图形运动，以及绘图4个方面对学生的空间观念进行培养[3]，每一个方面都需要空间推理能力作为基础．在小学阶段，“三视图”问题可以说是培养学生空间推理能力比较突出的方面．“三视图”中空间推理能力的类别见图6．

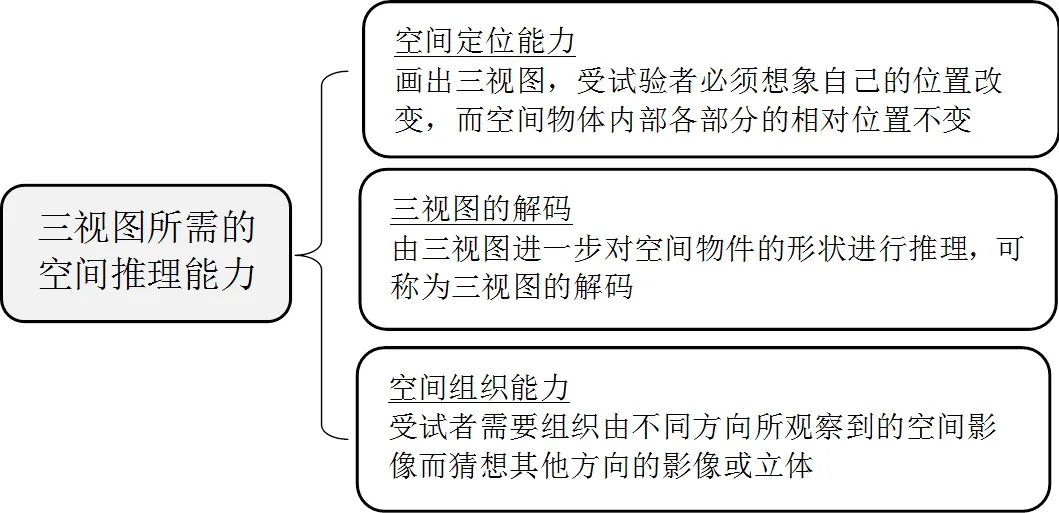
图6 三视图中空间推理能力的类别

“三视图”问题根据任务类型的不同可划分为两大类别：一类是“视图与立体图的对应”，包括由三维至二维空间组织（由立体图选出三视图）和二维至三维空间组织（由三视图选出立体图）；第二类任务为“视图与视图的对应”，包括不需额外假设的由右视图选出左视图问题，以及需要额外假设的，根据给定立体模型的前、俯两个视图判断第三个视图是否与之兼容，这一任务也被认为是难度最大的[28]．研究表明，在处理相关任务时，学生需要调动与运用不同的空间推理能力．主要涉及：第一，空间定位能力（spatial orientation），即在想象自己位置改变的同时，保持空间物体内部各部分的相对位置不变，特别体现在解决由三视图选出立体图的任务中；第二，三视图的解码能力（decoding），即通过二维的三视图对立体物件的形状进行推理；最后，空间组织能力（spatial organization），学生需要根据不同方向所观察到的空间影像而猜想其它方向的影像或立体图形，尤其体现在解决“视图与立体图”对应的问题中[28]．

类似涉及几何对象相互转换关系的教学任务还包括图形的切割与拼接、图形的展开与折叠等．实物操作在学生建立起三维与二维的转换、表象的加工与处理等过程中发挥着重要的作用，丰富的实物操作经验有助于学生经历空间推理的过程．在培养学生空间视觉化、直观想象的能力时，也要注重引导学生探索直观背后的规律，了解直观背后可能的“陷阱”，这也是空间推理的体现[29]．

4 小学数学教学中数学推理能力的培养

推理所包涵的范围甚广，无论是一般性地从不同视角来理解推理（如演绎和归纳推理、模仿和创造性推理等），还是具体到某一学习领域的数学推理（如代数推理、比例推理等），数学推理几乎渗透于全部数学学习活动．在上文中，尽管对在不同学习内容领域中的数学推理举了一些例子，未必能覆盖到全部．事实上，针对数学推理的教学，很难提出一个公认的程序或者步骤，一个一般意义上的实施原则与要求会更有灵活性．例如，全美数学教师协会分别从任务设计、课堂环境营造、鼓励课堂对话交流、恰当的评价交流和对教学实践的反思5个方面构建了关于提高学生数学推理能力的框架可作为推理教学的一种参考[30]．除此之外，尝试从以下两个方面为教师在教学中培养学生数学推理能力提供一些建议．

4.1 设计支持创造性推理的任务

在对推理类型的分析中，相比模仿性推理，学生进行创造性的数学推理要困难一些，但这又是学生数学素养中十分重要的部分．在利特纳看来，所谓创造性任务是允许学生进行独立思考和探索的任务[19]．这里的创造并非指任务设计的形式有多新颖或独特，而是指那些并不在事前给出提示或答案，允许学生进行独立思考和探索的任务，这样的理解，或许让一般的教师更容易操作，毕竟新颖、独特的教学任务设计并非易事．

利特纳发现，在瑞典教科书中死记硬背以及浅显推理的任务十分常见，高达80%的任务都能够通过简单的策略模仿进行解决．在这种任务中，学生需要做的就是记住其中的程序与策略，并将其应用于新的任务之中．教材不等于学材．因此，教师教学中需要根据教材内容进行适当的设计，引导学生进行探究．如在呈现“平行四边形面积”的探索过程时（见图7）[31]，教材以铺草坪为背景要求学生计算平行四边形的面积．在同一页面中首先引出辅助线作为提示，接着又进一步引导学生思考其与长方形面积的关系，并建议借助方格纸进行观察，最后则直接通过图片呈现割补过程，要求学生总结出相应的面积公式．从教材的呈现可以看出，教师需要引导学生经历探索过程，但如果学生在独立预习或课堂学习时只是对教材中的提示进行检验，没有真正经历思考由长方形、三角形与平行四边形的关系而推理出采用割补法计算面积的过程，这一内容也就变成了简单的策略模仿．

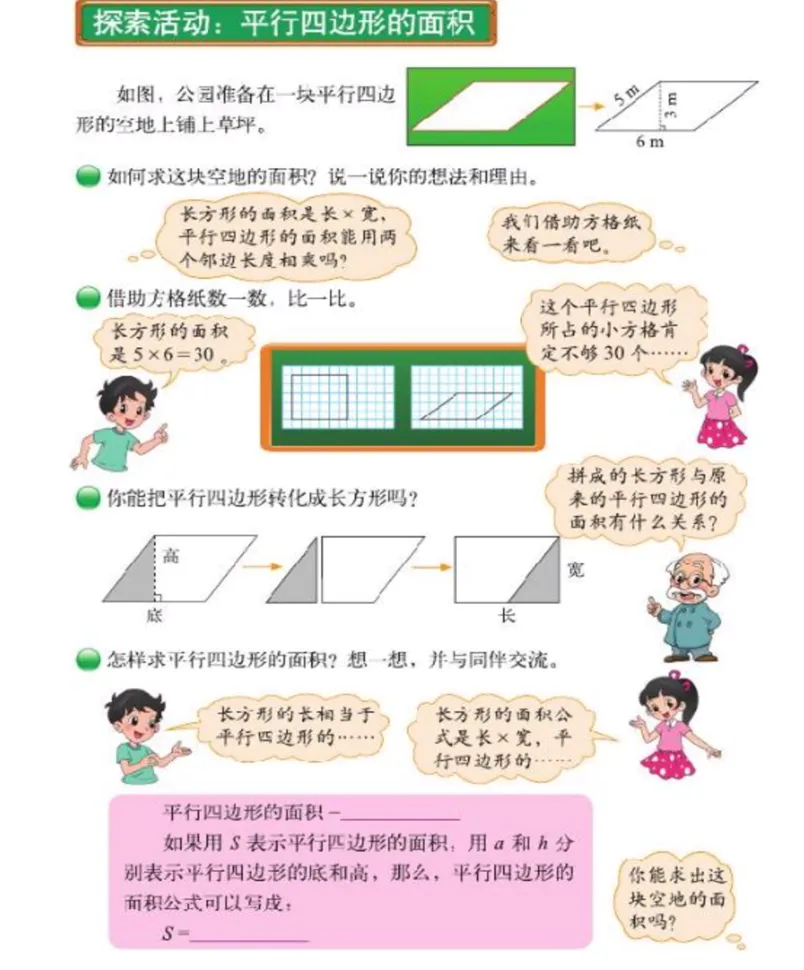
图7 数学教材中的推理任务

再比如教学圆锥体积的时候，如果只关注推理的结果，老师只要拿一个圆锥和一个同它等底等高的圆柱（下简称圆锥与圆柱），用水或者沙“倒”给学生看，看到倒3次刚好倒满，得到圆锥体积是圆柱体积的三分之一就可以了．如果从关注推理的过程出发，教学过程则可能完全不同．教师先让学生猜测圆锥与圆柱体积之间有什么关系，如果不是提前学习过，学生会用面积的知识类比推理成也是一半的关系（如图8所示）．这是一个有趣的类比推理过程；如果在此基础上教师进一步引导学生发现结论为什么不正确，进而分析正确的结论可能是怎样的，学生可能呈现出的思考过程将有很大的可能是具有创造性的，这种猜测和推理验证的碰撞，也会调动学生探索数学的动机．

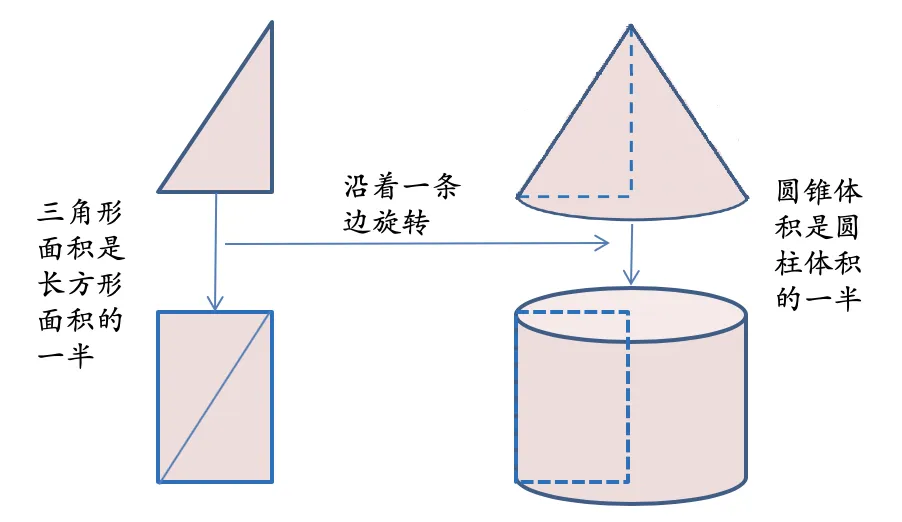
图8 学生对圆锥体积与等底等高的圆柱体积关系类比推理的思考

为更好地设计相关教学任务，教师可以尝试根据前文中结构视角下不同推理的表现图示描画出学生的不同推理过程．在选择、设计与运用教学任务时，教师需要给学生提供做出猜想与假设、调动与提取已有知识进行验证与修改的机会，使得学生经历提出观点、寻找证据支持与反驳、修改观点等推理过程，在寻找答案中提高数学推理的能力．相比一般的任务布置，创造性推理任务较为费时，它不仅需要教师分析进行“创造性”知识的难度，筛选问题情境与活动，还需要教师能够在探索的过程中给予学生适度但具有反馈性的指导．学生思考和完成这样的任务需要时间，如能将课内创造性的推理活动延伸至课外，或能克服时间上的障碍，课内和课外学习活动相结合也会是培养推理能力的途径．这也需要做进一步的实证检验．

4.2 鼓励学生解释与表达推理的过程

学生能够得到正确的答案却无法提供解释是数学教学中的常见现象，他们常常无法通过提供证据、进行对比等方式解释和说明自己的做法和看法．研究者以一个教学研究中的例子来说明．

研究者请学生解释：为何“1，4，7，10，13，16…”数列中永远不会出现3的倍数．完整的解释应同时提及“因为数列由1开始”和“得到数字永远比3的倍数多1”两个方面．学生有3类常见的解释：第一类是不断地重复结论或者题目中的要求，而非提供证据作为支持，如“因为规律是加3，所以你是无法得到3的倍数”；第二类则是提出某个例子，但并没有得出一般化的结论，如“7是其中的一个数字，它不是3的倍数”；第三类学生只能提及数列起点是从1开始，或将数列中的数字同3的倍数做比较，缺少推理的细节[32]．学生并不是没有想法，而是无法建立起完整的推理思路．因此，教师在教学中可有意识地引导学生对得到答案的过程进行描述，逐步学会使用逻辑词“如果…，就会…”“因为…，所以…”等，学生解释的过程正是他们为自己的观点寻求证据，应对质疑的推理过程，这个过程也帮助他们学会数学地表达．

培养学生的数学推理能力是数学教学的重要目标．在最新PISA 2021的数学能力框架中，学会数学地推理是学生数学素养的一个核心部分[1]．尽管研究者对什么是推理、推理的不同类型等进行了概括与分析，但小学阶段的推理教学着力点更需要关注推理过程中学生经历的心理过程．教师在教学中不用过于纠结到底是演绎推理还是合情推理，也不需要严格区分这到底是模仿推理还是创造性推理，更要看是基于哪些证据或既定假设得出什么样的结论，要看到学生各自是如何思考与表达，这就是在和学生一起经历数学推理的过程．比如从一个猜想开始，寻求可能的答案；亦或对于一个已知的结果，说出可能的道理．

数学推理的过程蕴含着个人的推断和思考，这种思考既有批判性思考也有创造性思考．学生需要能批判地检验所得的观点和结论是否正确，他们也可能在推理中进行创造，产生新的策略和方法．因此，学会推理，并不是在某一堂推理课，某一个特殊的年级才开始，它贯穿于数学教育的整个过程．让推理教学要有法可循的关键是教师需要具备推理的意识和思维．掌握推理的方法需要大胆猜想，小心求证，教授推理的要义在于教会学生言之有理、言必有据，这也真正体现了数学学科的学习特点．

[1] OECD. PISA 2021 mathematics framework [M]. France: OECD Publishing, 2018: 8.

[2] 课程教材研究所．20世纪中国中小学课程标准教学大纲汇编（数学卷）[M]．北京：人民教育出版社，2001：49．

[3] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：6–7，22．

[4] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：北京师范大学出版社，2018：5．

[5] 核心素养研究课题组．中国学生发展核心素养[J]．中国教育学刊，2016（10）：1–3．

[6] YACKEL E, HANNA G. Reasoning and proof [M] // KILPATRICK, MARTIN W G, SCHIFTER D. A research companion to principles and standards for school mathematics. Reston: NCTM, 2003: 227–236.

[7] TOULMIN S, RIEKE R, JANIK A. An introduction to reasoning [M]. New York: Macmillan, 1984: 10, 14.

[8] TOULMIN S E. The uses of argument [M]. New York: Cambridge University Press, 2003: 89–99.

[9] MOSHMAN D. From inference to reasoning: The construction of rationality [J]. Thinking & Reasoning, 2004, 10 (2): 221–239.

[10]  LITHNER J. A research framework for creative and imitative reasoning [J]. Educational Studies in Mathematics, 2008, 67 (3): 255–276.

[11]  THOMPSON P W. Imagery and the development of mathematical reasoning [M] // STEFFE L P, NESHER P, COBB P, et al. Theories of mathematical learning. Mahwah: Erlbaum, 1996: 267–283.

[12] 史宁中．漫谈数学的基本思想[J]．数学教育学报，2011，20（4）：8．

[13] 郭玉峰，史宁中．“数学基本活动经验”研究：内涵与维度划分[J]．教育学报，2012，8（5）：23–28．

[14]  JEANNOTTE D, KIERAN C. A conceptual model of mathematical reasoning for school mathematics [J]. Educational Studies in Mathematics, 2017, 96 (1): 1–16.

[15]  PEDEMONTE B. How can the relationship between argumentation and proof be analyzed [J]. Educational Studies in Mathematics, 2007, 66 (1): 23–41.

[16] PEIRCE C S. Sixth paper: Deduction, induction, and hypothesis [M] // COHEN M R. Chance, love, and logic: Philosophical essays. New York: G. Braziller, 1956: 131–153.

[17] REID D A, KNIPPING C. Proof in mathematics education: Research, learning, and teaching [M]. Rotterdam, The Netherlands: Sense Publishers, 2010: 83–128.

[18]  CONNER A M, SINGLETARY L M, SMITH R C, et al. Identifying kinds of reasoning in collective argumentation [J]. Mathematical Thinking and Learning, 2014, 16 (3): 181–200.

[19]  LITHNER J. Students’ mathematical reasoning in university textbook exercises [J]. Educational Studies in Mathematics, 2003, 52 (1): 29–55.

[20] NATHAN M J, KOELLNER K. A framework for understanding and cultivating the transition from arithmetic to algebraic reasoning [J]. Mathematical Thinking and Learning, 2007, 9 (3): 179–192.

[21] Ontario Ministry of Education. Paying attention to algebraic reasoning——Support document for paying attention to mathematics education [M]. Ontario: Queens Printer for Ontario, 2013: 10.

[22]  KIERAN C. The learning and teaching of school algebra [M] // GROUWS D A. Handbook of research on mathematics teaching and learning. New York: Macmillan, 1992: 390–419.

[23]  STEFFE L P. Schemes of action and operation involving composite units [J]. Learning and Individual Differences, 1992, 4 (3): 259–309.

[24] TZUR R, JOHNSON H L, McCLINTOCK E, et al. Distinguishing schemes and tasks in children’s development of multiplicative reasoning [J]. PNA, 2013, 7 (3): 85–101.

[25]  CRAMERK, POST T, CURRIER S. Learning and teaching ratio and proportion: Research implications [M] // OWENS D T. Research ideas for the classroom: Middle grades mathematics. New York: Macmillan, 1993: 159–178.

[26]  MODESTOU M, GAGATSIS A. Cognitive and metacognitive aspects of proportional reasoning [J]. Mathematical Thinking and Learning, 2010, 12 (1): 36–53.

[27]  CLEMENTS D H, BATTISTA M T. Geometry and spatial reasoning [M] // GROUWS D A. Handbook of research on mathematics teaching and learning. New York: Macmillan, 1992: 420–464.

[28] 陈韵如，杨凯琳，林福来．小学高年级学生在立方体积木三视图的推理表现[J]．台湾数学教育期刊，2018，5（1）：1–34．

[29] 张侨平，邢佳立．空间观念的培养——以“立体图形的分割和拼接”为例[J]．小学数学教师，2019（9）：8．

[30]  NCTM. A teacher’s guide to reasoning and sense making [EB/OL]. (2012–04–04) [2020–05–20]. https://www.nctm.org/ uploadedFiles/Standards_and_Positions/Focus_in_High_School_Mathematics/FHSM_TeacherGuide.pdf.

[31] 小学数学五年级（上）[M]．北京：北京师范大学出版社，2016：53．

[32]  EVENS H, HOUSSART J. Categorizing pupils’ written answers to a mathematics test question: I know but I can’t explain [J]. Educational Research, 2004, 46 (3): 269–282.

Mathematical Reasoning in Primary Mathematics Instruction: Theories and Practice

ZHANG Qiao-ping1, XING Jia-li2, JIN Xuan-zhu3

(1. Department of Mathematics and Information Technology, The Education University of Hong Kong, Hong Kong 999077, China;2. Teaching Monthly, Zhejiang International Studies University, Zhejiang Hangzhou 311002, China;3. YungWing School Zhuhai, GuangdongZhuhai 519060, China)

Mathematical reasoning is the core component of mathematics learning. There are many different views on the definition of reasoning and forms of mathematical reasoning. This article first analyzes four different perspectives for understanding mathematical reasoning, which include product, process, structure, and imitation and creation. Based on this understanding, we examine the specific forms and teaching of mathematical reasoning in three domains of primary mathematics: Algebra, Proportion, and Space. To promote students’ mathematical reasoning ability, we suggest that teachers design creative reasoning tasks in mathematics teaching and encourage students to explain and communicate mathematically.

mathematical reasoning; mathematics learning; primary mathematics teaching

G620

A

1004–9894（2021）05–0001–07

张侨平，邢佳立，金轩竹．小学数学教学中数学推理的理论和实践[J]．数学教育学报，2021，30（5）：01-07．

2021–05–02

香港教育大学博文及社会科学学院院长研究基金（TFG-10-MIT2019-0030）；MIT学系教学合作研究基金（MIT2019-0018）

张侨平（1980—），男，湖北武汉人，助理教授，主要从事数学情感和数学问题解决、数学课程改革和数学教师教育研究．

[责任编校：周学智、陈汉君]