基于BEA的个体问题解决干预有效性研究

于文华，王光耀，蔡金法

基于BEA的个体问题解决干预有效性研究

于文华1，王光耀1，蔡金法2

（1．山东师范大学 数学与统计学院，山东 济南 250014；2．美国特拉华大学 数学系，纽瓦克 19716）

对学习有困难的个体使用各种干预措施以促进其问题解决，并使用简要实验分析（BEA）作为手段来分析各种干预措施之有效性．设计了4个实验分析阶段（基线阶段、单一干预阶段、扩展分析阶段、泛化阶段），根据单一干预阶段得到的初始结果，评估单一干预阶段和扩展分析阶段的结果之间的一致性，然后通过泛化阶段进行实验结果的验证以及问题解决能力的保持与深化．研究结果表明，BEA能够有效预测提高学生问题解决能力的最有效干预措施．对所有3名学生，BEA预测的最有效干预与学生的扩展干预分析结果一致，并在泛化阶段继续保持有效性．

实验分析（BEA）；干预；有效性；可视化分析

1 问题提出

许多学生都在努力地学习，但某些学生的学业成绩特别是数学成绩却不理想．数学技能的丧失被发现是造成学习障碍的第二大因素[1]．而数学教育的成功对所有学生都很重要，因为它为学生提供了额外的教育选择，并增加了学生未来职业生涯的前景和收入潜力．因此，很多研究人员和教育工作者都呼吁用干预措施和评估方法来解决个体学业成绩特别是数学成绩的不足[2]．

MTM（math to mastery）作为一种典型的干预措施，是一个结构化的干预程序，包括预览问题、重复练习、立即纠正反馈、总结和形成性反馈以及对进展的自我监控[3]．MTM对学生计算流利性的有效影响已经在研究中得到了证实[4]．CCC（cover-copy-compare）是另一种有效的数学干预措施，旨在提高各种数学计算技能的准确性和流畅性[5]，也能有效地解决数学技能缺陷以及拼写和写作技能方面的问题[6]．另外，广泛认可的干预措施，还有TP[7]和CTD[8]等．

虽然上述干预措施都已被证明在提高数学基础计算流利性方面是成功的，但选择最有效的干预措施往往是困难的，因为学生可能会遇到的学术问题原因有很多[9]．事实上，Lentz指出学术问题原因可以描述为技能缺陷、流利程度问题、问题表征，或者这些因素的某些组合[10]．因此，利用评估工具，将学生需求与适当的教学干预相匹配是至关重要的[11]．

简要实验分析BEA（brief experimental analysis），是一个较为可靠的、时间效率和成本效益较好的选择和评估干预措施的工具．在BEA中，首先评估个体的反应，建立与目标行为相关的基准表现水平．然后将此级别的性能与多个干预、干预组件或干预组件的组合进行比较，目的是确定每个学生最有效的干预措施[12]．因此，这个简短的评估程序允许实践者快速尝试几种干预措施并评估学生的反应，然后选择其中一种较为成功的干预措施进行全面实施，而不必要花费时间、金钱和其它资源实施不成功或中等成功的干预措施．在进行了大量分析的测试中[13]，在BEA中被确认为有效的干预措施，与其它干预措施相比较，还能够继续产生良好的效果．

尽管BEA作为一种干预选择和评估的工具在阅读流利性[14–15]和计算流畅性领域[16]取得了成功，但很少有研究考察将BEA应用于数学领域的可行性[17]，对于个体问题解决的干预与评估更显不足．这里的研究正是基于BEA的选择和评估作用，通过不同实验阶段的可视化分析来评估多个不同干预措施之有效性，进而选择出合适的干预措施来促进个体问题解决．以勾股定理的应用之一即最短路径为研究材料，设计了3个实验阶段：单一干预阶段、扩展分析阶段与泛化阶段，根据研究中问题材料的特殊性，采用以下两种干预措施：MTM干预、CCC并结合学生动手操作干预．

2 研究方法

2.1 研究目的

通过比较两种干预措施对个体问题解决的影响，进而选择出最有效的干预来促进个体问题解决．因此，研究目的是通过比较所有的干预措施，来评估单一干预阶段、扩展分析阶段与泛化阶段的结果．具体来说，提出以下3个问题．

（1）学生是否会在单一干预阶段中对不同干预表现出不同反应？

（2）学生在单一干预阶段中对干预的反应是否能预测学生在扩展分析阶段中对干预的反应？

（3）在扩展分析阶段中被确定为最有效的干预措施是否会在泛化阶段继续有效？

2.2 参与者和背景

参与者是来自某县城普通初中的3名初中二年级学生，记为A、B、C，A数学学业成绩好于B，B又好于C．A、B均为县城户籍，而C是农村户籍转学学生．按照实验研究的程序，获得了参与者的同意，并获得家长同意．此外，根据学校记录和家长谈话，这些学生没有接受特殊教育或其它数学干预．

这3名参与者是通过多个步骤挑选出来的：首先随机选取了30名学生作为潜在的参与者，然后根据数学老师掌握的学生在校学习情况，排除了21名学生，原因包括特别突出的课堂表现和接受其它数学辅导，最后在剩余的9名学生中，通过一般教学水平的问答题排除了6名学生，他们的回答表现明显高于或者低于一般教学水平．剩余的3名学生作为研究的参与者．

2.3 实验设计

2.3.1 实验因变量和SPPM编码

在以前的研究中[18]，为了研究运算的流畅性，研究者将产生最大效果的干预措施确定为扩展干预分析中最有效的干预，并将每分钟正确位数（correct digits per minute，简称CDPM）设定为研究的主要因变量．根据Reisener等人的指导[16]：当适当的数字写在适当的栏中时，得分为正确，将正确数字的数目除以总秒数，再乘以60即为CDPM的值．

考虑到针对勾股定理的应用能力体现在对勾股定理运用的准确性、流畅性，具体到解决最短路径问题，可将正确率与完成速度作为可视化指标．因此，将每分钟得分数（score points per minute，简称SPPM）作为主要因变量．将顺利解决这一问题的全部过程进行了分步，每一步的顺利解决都会获得一定的分数，当被试提出他（她）完成问题解决后，实验者结束计时并对被试的解决方案进行评分，将最终得分除以总秒数，再乘以60，得到一个SPPM值．

2.3.2 实验阶段

实验包括基线（baseline）、单一干预、扩展分析以及泛化4个阶段．通过筛选选出合适的被试，测出基线水平．在单一干预阶段采用了交替处理设计．实验条件（MTM和CCC）均在单一场合给出．在每个条件实施后，最有效的干预被确定为产生最高SPPM的干预．在扩展分析过程中，还使用交替处理设计来比较基线效果与干预措施影响下的效果．每天只进行一次干预．干预条件被平衡以控制潜在的结转和顺序效应．

基线阶段：在基线阶段，学生尝试完成3份难度相似的勾股定理基础问题，没有接受任何干预，直到他（她）们表现出较为稳定的状态，便完成基线阶段的测试．由于参与者首次接受测试、测试的环境等一系列客观因素，会出现有的实验数据波动较大的情况，并不能完全客观地反映出参与者问题解决的真实水平．因此，将不能客观反映学生水平的数据排除，得到了波动不大的3个数据点，反映出的参与者知识水平称之为稳定的状态．

单一干预阶段：单一干预阶段是在一个稳定的基线下进行的，以检查所选择的干预条件对每个学生勾股定理应用的影响．在此阶段，首先利用单一干预阶段的材料让3位学生自己独立求解，不涉及任何干预，为了和干预形成对比，称为控制条件．然后进行以下两种干预，干预顺序是随机选择的，所有干预均在一天内实施．为了避免练习效应，每次练习结束后提供一小时的休息时间．

MTM干预：步骤是基于Mong等人开发的《掌握数学干预手册》[19]．在学生解决问题的过程中，考官首先解释解决问题的每一步．随后，学生根据考官的讲解，努力理解思考直到获得顺利解决这一问题的方法并完成问题．在学生完成每个问题时，如果学生出现了错误，考官立即给出纠正反馈．在每两分钟的数学测试后，考官立即计算学生的SPPM值，同时也对每次测试的努力和表现给予表扬，学生在每一分钟的数学测试结束时完成一个自我监控图表，以直观地显示他的表现．平均每个参与者的MTM过程持续10分钟．

CCC结合动手操作干预：在一次CCC干预过程中，学生首先被要求看材料左侧呈现的问题与答案，同时提供实物模型让学生亲自动手操作，通过不断地尝试找到最短路径所在．Cover过程：考官将左侧的问题与答案覆盖．Copy过程：让学生解决右侧相同的问题．Compare过程：学生独立完成题目后，去掉索引卡，将学生的答案与原答案进行比较．如果题目回答正确，学生则顺利完成了这一问题．如果回答错误，则通过将其响应与正确响应进行比较，立即提供纠正反馈．为了保证程序的准确执行和保持分析的内部有效性，使用了提示．在CCC过程结束后，立即对该学生进行评分，作为CCC过程的SPPM值．CCC干预平均持续约5分钟．

扩展分析阶段：每一种干预条件都以一种平衡的顺序呈现，这样，没有一种干预之后是相同的干预．每天午餐前进行一次干预．所有的干预措施都采用以前研究中概述的标准程序．

泛化阶段：为了评估BEA在选择可能推广到目标单一技能之外的干预措施时的预测有效性，使用多技能等级探针评估学生对勾股定理应用的推广和掌握情况．所有的泛化课程都是在午餐后进行的，这样每个学生在午餐前都会有一个针对性的单技能课程，午餐后会有一个多技能课程．

2.4 实验材料

在各阶段使用的实验材料，是以北师大版数学教材八年级上册第一章勾股定理的内容为基础，主要围绕解决最短路径问题来设计，而具体到每个阶段又有所不同．

在基线阶段使用的材料将从勾股定理的概念、几何意义、简单应用这3个方面入手，设计6个问题，每次测试两个问题．

在单一干预阶段为每个干预设计了相应的干预材料．在MTM阶段使用的材料，设计了一个经典的最短路径问题（圆柱侧面上两点之间）作为原型，要求学生在主试者的引导下完成这一问题．在CCC阶段使用的材料，左侧列出了同样的最短路径问题，并且附带正确的答案及解决思路，而在材料右侧列出了同样的问题，但是没有答案．要求学生在CCC干预和自己动手操作之后，完成右侧的问题．

在扩展分析阶段，以经典原型为基础设计4个变型问题，即母线上给定比例位置问题、绕若干圈问题、折回问题、特殊位置问题，但都仍然在圆柱这一模型上考虑．

在泛化阶段，同样以经典原型为基础，设计了3个变型问题，即台阶最短路径问题、正方体最短路径问题、长方体最短路径问题，都跳出圆柱这一模型考虑．

2.5 实验过程

对每位学生，3次完成基线的测量，3次完成控制条件与单一干预，12次完成扩展分析阶段，6次完成泛化阶段．每一天的课程结束以后，将学生的结果进行整理分析，记录在表中．

3 实验结果

3.1 基线阶段和单一干预阶段

图1显示了3个学生的基线和单一干预结果．总体来看：MTM干预对学生A和学生B的干预效果较好，CCC结合动手操作干预对学生C的干预效果最好．具体结果如下．

学生A在基线期间的SPPM均值为5.6，之后的单一干预阶段结果显示在MTM条件下获得最高的SPPM值．学生B在基线期间的SPPM均值为4.6，之后的单一干预阶段结果显示在MTM条件下获得最高的SPPM值．学生C在基线期间的SPPM均值为2.8，之后的单一干预阶段结果显示在CCC结合动手操作条件下获得最高的SPPM值．

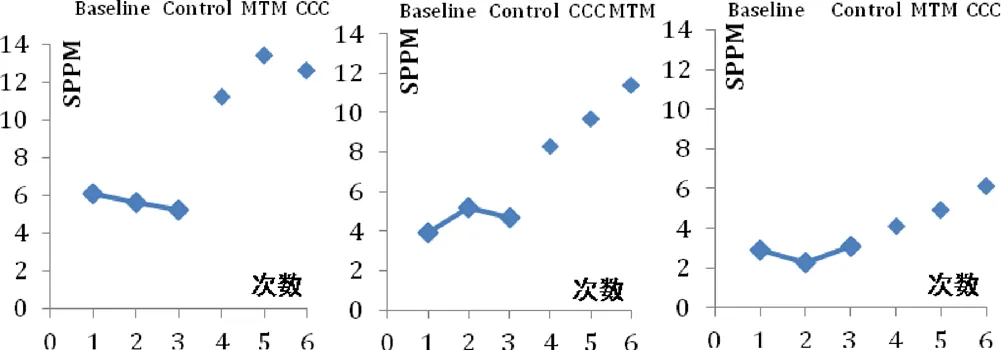
图1 基线阶段和单一干预阶段学生A学生B学生C的SPPM值

3.2 扩展分析阶段

图2显示了针对3个学生的扩展干预的结果．总体来看：针对每一位学生，两种干预条件的结果均显示出较基线水平的提高，并且干预结果基本都为上升趋势．具体来看：

学生A的基线SPPM均值为6.5（范围是5.8～7.4），MTM均值为10.1（范围是8.4～12.3），CCC结合动手操作均值为8.9（范围是7.2～10.3）．学生A都是在MTM条件下获得了他SPPM值的最高中位数点（10.6）和SPPM值的最高平均数点（10.1）．在这一阶段的4次实验中，基线和MTM数值均呈上升趋势，CCC结合动手操作数值前3次均为上升趋势，第四次与第三次基本保持持平．容易观察到，MTM数值线一直在CCC结合动手操作数值线的上方，并且有一定的距离．学生B的基线SPPM均值为5.9（范围是4.7～6.9），CCC结合动手操作均值为9.3（范围是7.1～11.2），MTM均值为10.0（范围是7.8～12.2）．学生B都是在MTM条件下获得了她SPPM值的最高中位数点（10.0）和SPPM值的最高平均数点（10.0）．在这一阶段的4次实验中，基线、MTM和CCC结合动手操作均呈上升趋势．容易观察到，MTM数值线一直在CCC结合动手操作数值线的上方，但距离不大．学生C的基线SPPM均值为3.1（范围是2.5～3.7），MTM均值为4.6（范围是3.2～6.1），CCC结合动手操作均值为5.7（范围是4.6～6.4）．学生C都是在CCC结合动手操作条件下获得了她SPPM值的最高中位数点（5.8）和SPPM值的最高平均数点（5.7）．在这一阶段的4次实验中，基线和CCC结合动手操作数值均呈平稳上升趋势，MTM数值呈波动上升趋势．容易观察到，CCC结合动手操作数值线一直在MTM数值线的上方．

图2 扩展分析阶段学生A学生B学生C的SPPM值

3.3 泛化阶段

图3显示了3个学生泛化的结果．总体来看：从扩展分析阶段选择出的干预措施的结果与泛化阶段的基线（general baseline）结果均有所不同．具体来看：学生A的泛化基线SPPM均值为8.0（范围6.7～9.1），施加的MTM条件的SPPM均值为10.7（范围9.9～11.4），MTM数值线一直在泛化基线数值线的上方，且有一定的距离；学生B的泛化基线SPPM均值为7.2（范围6.4～8.3），施加的MTM条件的SPPM均值为7.7（范围7.3～8.5），MTM数值线与泛化基线数值线均呈上升趋势，且上升幅度相似；学生C的泛化基线SPPM均值为3.6（范围2.7～4.6），施加的CCC结合动手操作条件的SPPM均值为3.7（范围3.4～4.1），泛化基线数值线平稳上升，CCC结合动手操作数值线有小幅度波动，基本保持平稳．

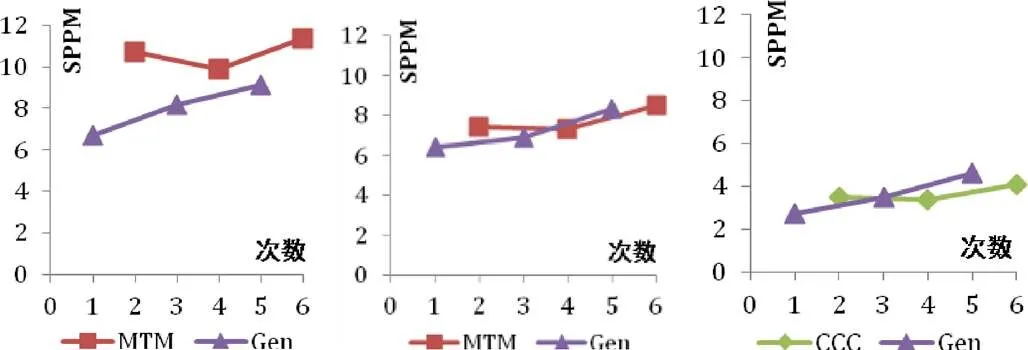
图3 泛化阶段学生A学生B学生C的SPPM值

4 讨论与总结

以往在数学领域运用BEA进行的学术干预主要针对数学计算流畅性，研究针对个体问题解决的能力，通过BEA对干预措施进行选择与评估，并根据提出的3个研究问题进行研究与分析．

研究结果表明，对学生A和学生B，在单一干预阶段中最有效的干预措施（MTM）在扩展分析阶段和泛化阶段继续保持了有效性．对学生C，在单一干预阶段中最有效的干预措施（CCC结合动手操作）在扩展分析阶段保持了有效性，在泛化阶段的干预结果比泛化基线水平略低．可能的原因是学生C的基线情况一直处于较低水平的稳定状态，鉴于此，学生C可能会对各种干预措施都做出一定的反应，但差异性不强．相比较而言CCC加动手操作干预要比MTM干预对学生C的效果好．但对于学生A、B、C，BEA均能够预测提高个体问题解决能力的最有效干预措施．综上，这些研究结果支持BEA在为每个学生确定适当干预措施方面的有效性和实用性．

关于第一个研究问题，即在单一干预中，学生是否会对不同干预表现出不同反应．在实验中，3名学生在单一干预阶段对不同干预措施的表现均不同，但表现结果并没有明显的差异．对于学生A、B来说，与平均基线和控制干预的SPPM相比，两种数学干预都导致了SPPM的增加，其中MTM产生了最大的SPPM值，但两种干预措施的结果差距并不明显．对于学生C来说，两种干预的SPPM值也均有增加，其中CCC结合动手操作的SPPM值最大，但结果差距同样不明显．所以，在单一干预阶段，学生虽然会对不同干预表现出不同反应，但结果差距并不明显，这样的研究结果与之前的研究结果相类似．因此，尚不清楚如果单独实施各种干预条件是否足以产生显著的差异反应．所以，今后的相关研究依然是必要的．

在单一干预阶段中，尽管从实验设计到实验实施环节都进行了随机处理以减少各个干预措施之间的影响，但各个干预措施之间缺乏明确的区别，也无法做到完全地区别实施．因此，关于被试不明显的表现结果，一个可能的原因是将多种干预措施结合起来实施和分析．也就是说，在学生运用勾股定理解决问题的某个环节中，学生们可能被多种干预影响，即使将独特的数学情境随机分配到不同的干预条件下，所有实验材料的解决、所有干预条件的影响都可能是结合的结果．因此，应用于某一个数学情境的干预条件可能会在其它干预条件下发挥作用．关于学生C不明显结果的另一个可能的原因是，她的基线SPPM值一直处于较低水平的稳定状态，鉴于此，学生C可能会对各种干预措施都做出一定的反应，但反应差异有限．

关于第二个研究问题，即学生在单一干预阶段对干预的反应是否能预测学生在扩展分析阶段中对干预的反应．对于所有3名学生，在单一干预阶段SPPM值最高的干预措施也是在扩展分析期间产生最高值的干预措施．对学生A来说，单一干预阶段最高SPPM值的MTM干预在扩展分析阶段依然产生了最高的SPPM值，且与控制组和CCC结合动手操作干预的差距较为明显．对学生B来说在单一干预阶段也是MTM干预产生了最高的SPPM值，在扩展分析阶段，虽然MTM干预与CCC结合动手操作干预的结果差距并不明显，但MTM干预的SPPM值依然是最高的．对学生C来说，单一干预阶段最高SPPM值的干预为CCC结合动手操作，在扩展分析阶段此干预也产生了最高的SPPM值．因此，尽管学生们在单一干预阶段表现出的不同反应并没有明显的差异，但所有学生在扩展分析期间都表现出对单一干预阶段最有效干预的持续积极反应．因此，研究结果表明，学生在单一干预阶段对干预的反应成功预测了在扩展分析阶段对该干预的持续有效反应．

关于第三个研究问题，即在扩展分析阶段中被确定为最有效的干预措施是否会在泛化阶段继续有效．对于学生A，最有效的MTM干预在泛化阶段依然有效，并且相比泛化基线有明显提高．对于学生B，最有效的MTM干预在泛化阶段也持续有效，相比泛化基线有小幅提高．对于学生C，最有效的CCC结合动手操作干预比起泛化基线有略低的走向，但基本保持持平．因此实验结果表明，在泛化阶段最有效的干预措施仍在继续产生效果．

虽然研究有助于拓展数学领域中BEA的实证研究，但仍需注意研究以下问题．首先，应说明内部效度（例如，学生自身知识水平的成熟发展）和外部效度（例如，3名被试学生）对研究的影响．而针对这一问题，对不同人群进行重复研究或者选取多个参与者进行群体干预研究可能会是比较好的解决办法．第二，实验结果是特定数学问题情境下的干预结果，没有评估干预措施对课堂表现的泛化结果．因此，尚不清楚学生在课堂作业和测试中的表现是否会有相似的反应．但个体干预的设计有助于深入观察分析每个参与者的情况，能够对不同干预措施的效果提供客观可靠的数据支持，能够促进现实教学的策略多样化．也能够为以后相关群体干预、课堂教学干预、数学其它技能干预等研究提供支持．最后，研究针对的是中学生对勾股定理的应用能力．目前还不清楚干预措施是否适用于更复杂的数学技能．更复杂的数学技能可能需要多次、多种干预才能有明显改善．因此，数学干预在多大程度上概括了复杂的数学技能还不得而知．

综上所述，与基线相比，MTM干预和CCC结合动手操作干预均能有效提高个体问题解决能力．结果表明，MTM干预对其中两名学生的干预效果最好，而CCC结合动手操作干预对另外第三名学生的干预效果最好．关于BEA，目前的研究结果表明，BEA能够有效地预测在扩展分析阶段中每个学生最有效的数学干预．因此，BEA是一个有效的选择和评估工具，它能够使研究者快速地使用几个数学干预来确定最有效的干预措施，以便更有效地在每个学生身上实施并起到更好的作用．

[1] KAVALE K A, REESE J H. The character of learning disabilities: An iowa profile [J]. Learning Disability Quarterly, 1992, 15 (2): 74–94.

[2] FUCHS L S, FUCHS D. Principles for the prevention and intervention of mathematics difficulties [J]. Learning Disabilities Research & Practice, 2010, 16 (2): 85–95.

[3] MONG M D, DOGGETT A, MONG K W, et al. An evaluation of the math to mastery intervention package with elementary school students in a school setting [J]. Journal of Evidence-Based Practices for Schools, 2012 (13): 61–78.

[4] MONG M D, MONG K W. Efficacy of two mathematics interventions for enhancing fluency with elementary students [J]. Journal of Behavioral Education, 2010, 19 (4): 273–288.

[5] GRAFMAN J M, CATES G L. The differential effects of two self-managed math instruction procedures: Cover, copy, and compare versus copy, cover, and compare [J]. Psychology in the Schools, 2010, 47 (2): 153–165.

[6] MCLAUGHLIN T F, SKINNER C H. Improving academic performance through self-management: Cover, copy, and compare [J]. Intervention in School & Clinic, 1996, 32 (2): 113–118.

[7] ASPIRANTI K B, SKINNER C H, MCCLEARY D F, et al. Using taped-problems and rewards to increase addition-fact fluency in a first grade general education classroom [J]. Behavior Analysis in Practice, 2011, 4 (2): 25–33.

[8] KOSCINSKI S T, GAST D L. Use of constant time delay in teaching multiplication facts to students with learning disabilities [J]. Learn Disabil, 1993, 26 (8): 533–544.

[9] III E J D, MARTENS B K, WITT J C, et al. A model for conducting a functional analysis of academic performance problems [J]. School Psychology Review, 1997, 26 (4): 554–574.

[10]  LENTZ F E, EDWARD S. Functional assessment of the academic environment [J]. School Psychology Review, 1986, 15 (3): 346–357.

[11]  CODDING R S, SHIYKO M, RUSSO M, et al. Comparing mathematics interventions: Does initial level of fluency predict intervention effectiveness [J]. Journal of School Psychology, 2007, 45 (6): 603–617.

[12]  DALY E, MARTENS B, HAMLER K, et al. A brief experimental analysis for identifying instructional components needed to improve oral reading fluency [J]. Journal of Applied Behavior Analysis, 1999, 32 (1): 83–94.

[13]  ANDERSEN M N, DALY E J, YOUNG N D. Examination of a one-trial brief experimental analysis to identify reading fluency interventions [J]. Psychology in the Schools, 2013, 50 (4): 403–414.

[14]  BURNS M K, WAGNER D. Determining an effective intervention within a brief experimental analysis for reading: A meta-analytic review [J]. School Psychology Review, 2008, 37 (1): 126–136.

[15]  JONES K M, WICKSTROM K F. Done in sixty seconds: Further analysis of the brief assessment model for academic problems [J]. School Psychology Review, 2002, 31 (4): 554.

[16]  REISENER C D, DUFRENE B A, CLARK C R, et al. Selecting effective interventions to increase math computation fluency via brief experimental analyses: Math brief experimental analysis [J]. Psychology in the Schools, 2016 (53): 39–57.

[17]  CODDING R S, BAGLICI S, GOTTESMAN D, et al. Selecting intervention strategies: Using brief experimental analysis for mathematics problems [J]. Journal of Applied School Psychology, 2009, 25 (2): 146–168.

[18]  CARSON P M, ECKERT T L. An experimental analysis of mathematics instructional components: Examining the effects of student-selected versus empirically-selected interventions [J]. Journal of Behavioral Education, 2003, 12 (1): 35–54.

[19]  MONG M D, MONG K W. The utility of brief experimental analysis and extended intervention analysis in selecting effective mathematics interventions [J]. Journal of Behavioral Education, 2012, 21 (2): 99–118.

Research on the Effectiveness of an Individual Problem-Solving Intervention Based on Brief Experimental Analysis

YU Wen-hua1, WANG Guang-yao1, CAI Jin-fa2

(1. School of Mathematics and Statistics, Shandong Normal University, Shandong Jinan 250014, China;2. Department of Mathematical Science, University of Delaware, Newark DE 19716, USA)

Various interventions were used to promote problem solving in individuals with learning difficulties. Brief experimental analysis (BEA) was used to analyze the effectiveness of the various interventions. Four experimental analysis stages (baseline stage, single intervention stage, extended analysis stage, and generalization stage) were designed. Based on the initial results of the single intervention stage, the consistency between the results of the single intervention stage and the extended analysis stage was evaluated, and then the experimental results were verified and the problem-solving ability was carried through to the generalization stage. The results show that BEA can effectively predict the most effective intervention measures to improve students’ problem-solving ability. For all three students, the most effective intervention predicted by BEA was consistent with the results of the extended intervention analysis and continued to be effective in the generalization stage.

brief experimental analysis (BEA); intervention; effectiveness; visual analysis

G632.0

A

1004–9894（2021）05–0028–05

于文华，王光耀，蔡金法．基于BEA的个体问题解决干预有效性研究[J]．数学教育学报，2021，30（5）：28-32．

2021–06–11

教育部人文社会科学研究项目——基于BEA的个体问题解决干预有效性研究（20YJAZH124）

于文华（1978—），女，山东乳山人，副教授，硕士生导师，主要从事数学教育心理研究．

[责任编校：周学智、陈汉君]