初中数学教科书中概念的呈现方式及一致性研究

章 飞，俞梦飞，顾继玲

初中数学教科书中概念的呈现方式及一致性研究

章 飞1，俞梦飞1，2，顾继玲2

（1．江苏第二师范学院 课程与教学研究所，江苏 南京 211200；2．南京师范大学 教师教育学院，江苏 南京 210097）

在教科书梳理和编写团队交流的基础上，将教科书中概念呈现方式分为概念形成、概念同化、概念建构等4类8种；遴选专家型教师对初中数学教科书中所有概念进行一一研讨，得到概念呈现方式的应然状态；对人教版、北师大版初中数学教科书中概念呈现方式进行梳理，得到概念呈现方式的实然状态；建构一致性模型，基于模型发现：两个版本教科书中概念的呈现方式与应然状态之间一致度高，说明两个版本教科书中概念的呈现方式总体而言较为科学．调研也表明，一些与先前概念相似度高、先前学习经验丰富的概念，专家型教师认同类比建构的概念呈现方式，而现行教科书中都未有呈现，建议教科书设计中可尝试类比建构的概念呈现方式．

教科书；概念；呈现方式；一致性；初中数学

教科书，作为国家课程的体现，构成保障教育教学质量的第一道关口，因而，教科书设计研究成为教育研究中十分重要的一环．而概念作为数学思维的起点，其教科书呈现自然应引起研究者的重视．关于数学概念，已有研究主要集中于概念学习[1–2]、概念教学[3–4]、具体概念的编排[5–6]和概念理解的评价[7]等，对概念本身的分类、特征等进行研究不多[8–9]，其中关于教科书概念呈现的研究更是少之又少，有研究表明，一线教师对于教科书中概念呈现方式的认同程度不甚理想[10]．为此，作为教科书编写者，就需要思考数学概念的教科书呈现方式可以分成哪些类型？具体选择相应呈现方式的原则是什么？数学中的各个概念，教师比较认可的呈现方式是什么？现行教科书中概念呈现方式又如何？两者之间的一致性如何？这里以初中数学教科书为例进行探讨，相信这样的研究，对于教科书编制具有借鉴价值，同时也可以指导一线教师更好地理解教科书并指导教学．

1 概念呈现方式的类型分析

一套数学教科书中大大小小的数学概念可能有数百个，如初中数学阶段有近二百个，各自的呈现方式多样，为此，研究中首先得确定概念呈现的类型．关于概念的学习方式，研究颇多，多数学者采用奥苏贝尔的提法，认为概念学习有两种方式：概念形成与概念同化．所谓概念同化是指，以定义的方式直接揭示概念的本质，然后通过对概念的分类、比较、识别等活动，明确概念的内涵和外延，并与原认知结构中的有关概念建立联系．概念形成是指，从大量具体例子出发，从实际经验的肯定例证中，以归纳的方法概括出一类事物的本质属性[11]．也有学者认为还有一种学习方式：概念建构．概念建构，同样是希望学生经历概念的生成过程，但并不是通过对概念原型的归纳，而是通过具体的活动让学生自主建构[12]．然而由于种种原因，教科书中概念的呈现并不直接简单地匹配于这3种方式，即使采用了某一种方式，也往往会存在很多变化．为此，讨论教科书中概念的呈现方式，以便于教科书编者的选择使用，还需结合教科书的编写实际进行细分．正是基于上述考虑，团队在查阅多个版本初中数学教科书中概念，并与部分教科书编写者交流研讨后，确定了下面8种呈现方式．

方式A：不给出概念的严格定义，仅仅通过具体实例或者图示让学生感知．如，图1中几何体的概念呈现，图3中底角、顶角、腰、底边的概念呈现．

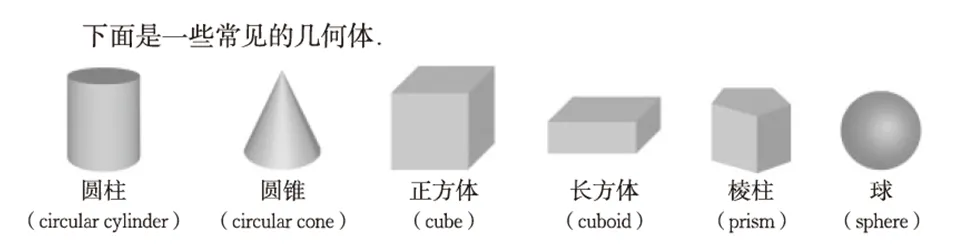
图1 有关几何体概念的教科书呈现

方式B：直接明晰定义，不予解释．如，图2所示教科书中的整式．

方式C：直接明晰定义，然后通过例子加以解释．如，图2所示教科书中的多项式、单项式的系数、单项式的次数．

图2 多项式有关概念的教科书呈现

方式D：提供单个例子或者图示让学生感知，然后明晰定义．如，图3中等腰三角形、等边三角形．

图3 等腰三角形有关概念的教科书呈现

方式E：提供较充分的例子或图示让学生感知，然后明晰定义．如，图4中函数的概念呈现，教科书中通过3个情境呈现了函数的不同背景和表示方式，并通过具体问题让学生感受了运动变化中的对应关系后，没有要求学生再行归纳，而是直接呈现了下面的函数定义．

图4 函数概念的教科书呈现

方式F：提供较充分的例子或图示让学生感知后，引导学生自主概括，然后明晰定义．这种方式相对于方式E，多了一个引导学生自主概括定义的过程．如，图5中一元一次方程的概念呈现，教科书在前面呈现了6个情境，并列出了相应的方程，然后设计了“议一议”活动，引导学生思考其中一些方程的公共特征，实际上，希冀学生自主归纳出一元一次方程的定义，借助教科书明晰了一元一次方程的定义．

图5 一元一次方程概念的教科书呈现

方式G：引领学生在活动中建构概念，明晰概念的定义．如，图6中平面直角坐标系的概念呈现，渐次递进地设计了3个活动，引领学生在活动中经历设计表格，借助数组表示位置，进而选取观察点（原点）利用数组确定位置，实际上，学生经历了一个坐标系的自我建构过程，后面明晰坐标系的概念就水到渠成了．

方式H：引导学生根据新概念的名称自主举例、建构概念，然后明晰定义．这种方式，中国教科书基本没有，但一线教学中多有尝试．如，一元二次方程的概念，教科书可采用类比建构的概念呈现方式．

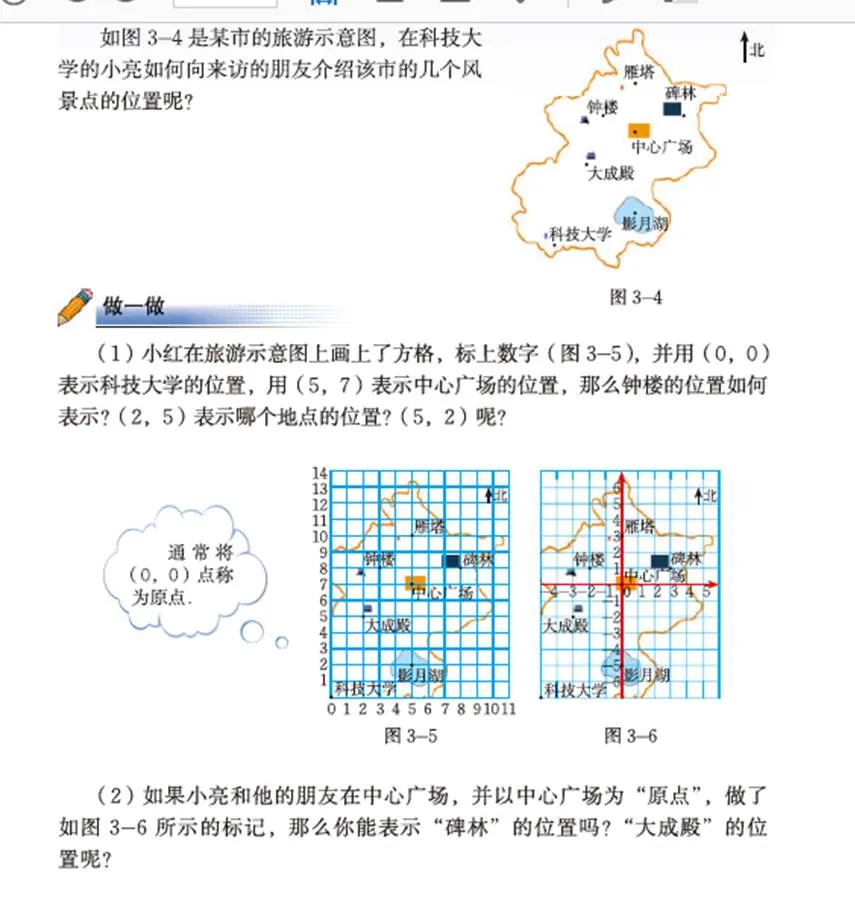
案例：类比建构的概念呈现方式（一元二次方程）

看到一元二次方程，你想到什么？

以前学习的哪些知识中遇到过“元”“次”这两个名词？

你能根据以前的学习经验，写出几个一元二次方程吗？

你能给一元二次方程下个定义吗？与同伴交流．

（说明：前面呈现的是学生活动，接着呈现活动的结论，即一元二次方程相对规范的定义．这段话教科书中不体现）

实际上，只含有一个未知数而且未知数的最高次数是2的整式方程，即形如2++=0（、、为常数，≠0）的方程，称为一元二次方程．

不同处理方式之间的关系，如图7所示．

图7 8种呈现方式之间的关系

图7中8个方框对应着8种呈现方式，7个棱形清晰地显示出了编写者在概念呈现方式选择时需要做出的几次判断，不妨将这7个判断依次记为P1、P2、P3、P4、P5、P6、P7．

此外，这8种呈现方式，大致可以分为4类．其中第一类，方式A，比较特殊，仅仅实例或图示感知，并不呈现严格定义；其余3类，实际上分别对应着概念学习的3种方式：概型同化、概念形成、概念建构．其中，方式B、C对应着概念同化，差别在于是否在教材中给出例子；方式D、E、F对应着概念形成，差别在于呈现原型例子的多少、是否明确要求学生自主归纳；方式G、H对应着概念建构，差别在于概念建构的方式．

2 概念呈现方式的选择依据分析

教科书编写时，编写团队对于概念的呈现自然有一些思考．但这样的思考，往往是比较零散的、个案的，也就是说，常常是针对具体的某个概念的呈现进行了较为深入的研讨，但尚未见到系统的总结提炼．只有适度总结提炼，才能更好地指导教科书的编写，同时也便于教科书编写团队的成长，特别是新编写人员的快速提升．为此，与编写团队成员进行了深度交流，并召集部分专家型教师进行了现场研讨，在研讨的基础上，形成了下面的判断依据．

P1，聚焦于是否给出概念的严格定义．数学是一门特别强调严谨的学科，而概念是思维的起点，因此，自然要求教科书中尽可能给出数学概念的严格定义．作为学习用的数学教科书，还需要关注给出概念严格定义的可行性和导向性，因此，在做出判断P1时，一般可以思考这样几个问题：概念能否被严格定义？概念的严格定义能否为该年龄段学生所理解？概念的严格定义是否对教与学产生好的导向作用？如果概念难以严格定义（如，点、线、面等）、概念的严格定义难以为该年龄段学生所理解（如，棱柱的严格定义需要用到线面垂直，对于初中生而言，这是比较难理解的）、概念的严格定义可能对教与学产生不好的导向，自然不必给出概念的严格定义了，而是通过情境让学生感知．

P2、P4，聚焦于教科书希望引导师生采用怎样的学习方式，概念同化、概念形成抑或概念建构．这里的影响因素较多，需要综合考虑概念的类型、概念的重要程度、学生有关该概念的前经验丰富程度，甚至教科书编写的理念与风格等．概念的类型，一般有对象性概念、度量性概念、观念性概念，如图8[12]．度量性概念，本是人类创造的产物，自然没有多少原型，无法采用基于原型概括的概念形成方式，一般采用概念建构，对应的教科书呈现方式是G；观念性概念，是多次感悟的产物，一般采用概念形成的方式，但由于观念性概念的严格表述，对学生而言比较困难，因此，可不要求学生归纳概念，而采用丰富例子感受后的教科书明晰，也就是对应的教科书呈现方式E．教科书中的概念，其重要程度并非完全一致的，考查整个概念网络，不难发现有一些概念成为后续概念学习的起点，有些概念在概念网络中是一个重要的结点，这些概念相对而言较为重要，而有一些概念位于概念树的末梢，相对而言不甚重要．一般而言，重要的概念，希望多展开其生成过程，以达成更为深刻的理解，可采用概念形成或概念建构的方式；而有的概念紧承前面的概念，是前面概念派生出来的，这样的概念，直接明晰定义即可，是否再给予例子解释，视概念理解的难度而定．而关于具体概念的学生学习经验以及概念形成的难易程度，更是影响概念呈现方式的一个重要因素，如果概念形成或者概念建构的难度超出了多数学生的能力水平，自然可以采用概念同化的形式，先给出概念的定义，再进行概念的理解；而概念原型丰富、特征明显的，可以采用概念形成的方式，通过对概念原型特征的归纳形成数学概念，当然，是否要求学生切实经历概念归纳过程，还需再行判断．此外，概念呈现方式，还与整套教科书的编写理念与风格有关，倡导探究学习的教科书，更倾向于采用概念形成与概念建构的方式，因此，概念呈现方式的具体选择，还会考虑与教科书整体风格的匹配．

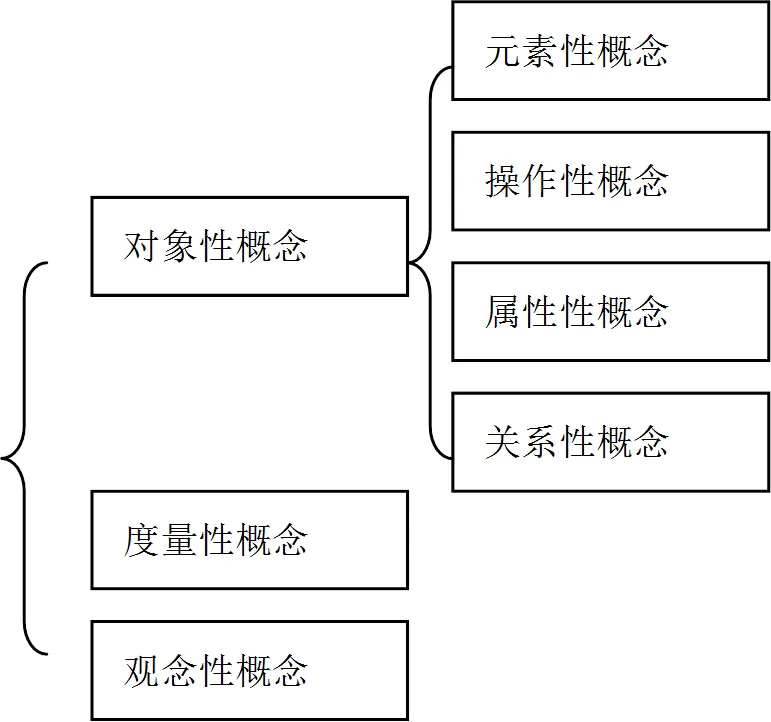
图8 概念的类型

P3，已经给出了概念的定义，是否再行举例解释，一般考虑两个因素：①是否有相关的例子，如一些采用外延定义的概念（如，实数：有理数和无理数统称为实数），定义已经说明了概念的外延，无法再行举例了．②学生理解的难度如何，仅仅定义，学生还未必能够很容易理解，一般应通过实例感知．例如，多项式次数的概念，定义“单项式中所有字母的指数和”相对抽象，在定义后，一般应给出具体的例子加以解释．

P5，是否要求学生归纳，自然需要考虑归纳的价值和难度了．如果概念归纳的价值不大，可以直接明晰概念．例如，三角形的概念，初中学生应该已经比较熟悉了，但要学生自主表述为“三条线段首尾相连形成的图形”，倒未必能够做到如此严格，也没有必要了．如果概念的特征比较内隐，学生自主归纳出概念本质的难度稍大，可以在具体例子感受的基础上，明晰定义，然后再加以解释．例如，初中函数的概念，其本质在于运动变化中的对应关系，但这样的关系是内隐的，学生自发地说出这样的共性难度较大，可以采用先明晰定义再解释的做法．

P6，主要关注例子的多少．一般而言，重要的概念、背景丰富的概念，应多给出几个例子，力图让学生形成更为全面的感受，避免单一例子的片面性，例如上面的函数概念，其背景就比较丰富，因此所举例子应兼顾生活实例和数学例子，同时其表现方式多样，可以有表达式、图象、表格等多种方式，因此所举例子也要尽量兼顾到这些不同的表现方式．

P7，关乎概念建构方式的选择．一般而言，类比建构要求学生能借助先前的学习经验，类比以前的概念，举出相关的例子，并在交流研讨中建构新概念，自然需要考虑学生先前学习经验的丰富性以及概念与先前学习概念的相似性．例如，分式（先前学习过整式、分数等相似概念）、一元二次方程（先前学习过一元一次方程、二元一次方程组，对元、次已经有了充分的感知），即可采取这样的方式．而一些度量性概念，如正切，本是人类创造性的产物，自然没有多少原型，无法概括；前面也没有多少经验，无法类比；常常基于现实问题，在解决的过程中，创生出新的概念．

综上，度量性概念建议采用方式G，观念性概念建议采用方式E，对象性概念是初中数学中占比最多的，情形也较为复杂，因此，无法给出一个统一的呈现方式．正如前文所分析的，需要综合考查其概念本身的重要程度、概念形成或建构的价值、概念先前的经验准备、概念背景的丰富性等，甚至兼顾教科书的整体风格，从而做出恰当的选择．当然，对象性概念中难以严格定义或者不甚重要的衍生性的概念，可以采用方式A．

3 概念呈现方式一致性的分析框架建构

分析教科书中概念呈现方式的一致性，需要解决几个问题：①具体概念呈现的应然方式和实然方式是什么？②如何将概念的呈现方式数量化？③如何刻画全书概念呈现方式的应然状态与实然状态的一致度？

对于教科书中具体某个概念呈现的实然方式，对照前面给出的8种方式，直接查阅教科书即可了解．对于教科书中具体某个概念呈现的应然方式，并无绝对客观的标准，只能基于专家教师的访谈，确定一个相对合适的呈现方式．这里的专家教师，除了优秀的一线教师外，教科书编写者也是一个当然人选，因为他们既有丰富的教科书编写经验，又多兼具一线教学经验，对教科书中概念呈现方式的判断能力较强．

依次分析概念的呈现方式A、B、C、D、E、F、G、H，发现：相邻概念呈现方式之间的差距较小，如，方式A与方式B的差异仅在于是否给出概念定义，方式B与方式C的差异仅在于是否给出例子解释；而不相邻的概念呈现方式之间的差异较大，如，方式A与方式E的差异就比较大，这不仅从对于两种方式的文字描述中可以看出，从图7中也可以发现两者之间存在5次判断的差异．基于上述考虑，将方式A、B、C、D、E、F、G、H分别赋值1、2、3、4、5、6、7、8．

这样，对于具体的某个概念Z，基于教科书查阅，得到该概念Z呈现方式的实然数值R；基于教科书编者和一线优秀教师的调查，并取平均值后，得到该概念Z呈现方式的应然数值Y；则|R-Y|刻画了概念呈现方式的实然状态与应然状态的差距．通过调查和分析，|R-Y|大于等于2时，两者就完全不一致了，其一致度为0，为此，概念Z呈现方式一致度的指标C定义如下：

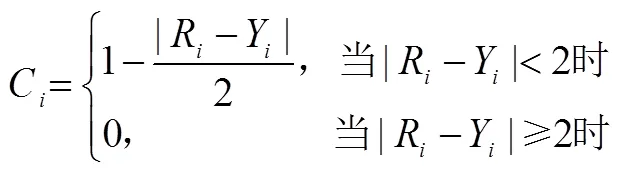
令整套教科书概念呈现方式的一致度为整套教科书中所有概念的呈现方式一致度C的平均值，即：

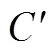
此外，还可以类似地比较两套教科书中概念呈现方式的一致度．以人民教育出版社教材（简记为PEP）和北京师范大学出版社教材（简记为BNUP）初中数学教科书为例，设概念Z在两套教科书中实际呈现方式对应的数值分别为P、B，则两套教科书中概念Z呈现方式一致度的指标C(B–P)定义如下：

两套教科书中概念呈现方式的一致度C为整套教科书中所有公共概念的呈现方式一致度C(B–P)的平均值，即：

4 两个版本教科书呈现方式一致性的数量分析

应然状态本应是一客观标准，但众所周知，与教学一样，教科书兼具科学与艺术的双重属性，概念的教科书呈现方式也难以给出一个客观的绝对标准．因此，为了解各概念的教科书呈现的应然状态，采用了专家型教师调研的方式．首先设计了调查问卷，对部分教科书编者和优秀数学教师进行调查．为提高调查的效度，精心遴选调查对象，委托部分省（市）教研员推荐了部分优秀数学教师，确保被调查者本身的专业素养；由于问卷涉及一百多个概念的呈现方式，需要耗费被调查者较多的时间，因此，事先和被调查者进行了充分沟通，确保这些被调查者在自愿的基础上认真完成调查工作；此外，在问卷中，首先结合具体案例介绍了概念呈现的8种方式，以便被调查者更为准确地理解概念的各个呈现方式的涵义，然后呈现下面的调查表；另外，难免出现部分概念的呈现方式难以选择，提醒老师实在难以选择，可以多选．2018年10月间，结合全国性的会议，选择性地发放问卷50份，最终收回有效问卷32份．但通过对这部分问卷的分析以及与部分被调查者的访谈，发现，采用问卷调查的方式，被调查者在短时间内，难能深入理解这8种呈现方式以及相互之间的关系，短时间内也难以形成准确的判断，这些影响了结果的有效性．

表1 概念呈现方式调查表

针对调查活动中发现的问题，为了提高效度，改用会议现场交流的方式．先后组织了两次现场研讨．第一次邀请了某省教育家型青年教师培养对象10人和教科书编者2人，第二次邀请了某出版社初中数学教材高级研修班学员20人，两次合计32人．现场研讨中，首先，详细介绍了8种概念呈现方式以及它们之间的关系；然后，共同商讨了具体呈现方式确定的程序和原则；接着以具体概念为例，进行了充分研讨，在研讨的基础上，每个参会者再做出自己的选择，填写问卷；最后，根据参会者的选择得到各个概念呈现方式的应然状态Y．大家普遍反映，现场会议研讨，对于概念呈现方式的理解更为全面深入，得到的应然状态数据更有效度；同时，这部分研讨者专业素养较好，而且现场先进行了充分研讨，研讨者对于应然方式的认识较为一致，总体稳定性较好，因此，下面关于概念呈现应然方式的数据，取自会议研讨的数据．

教科书中概念呈现的实然状态，是客观呈现的，查阅教科书并与8种概念呈现类型对照即可．当然，也存在极个别概念的呈现方式，兼具了某两种相邻呈现方式的特征，团队研讨后确定选择与其主体呈现更接近的呈现方式．

限于篇幅，表2呈现了北师大版和人教版初中数学教材中50个公共重要概念呈现方式的有关数据．

基于以上两方面的工作，利用上面的分析框架，得到了两套教科书概念呈现方式实然状态与应然状态之间的一致度的数据如下：

人教版：C=0.64，

北师大版：C=0.58．

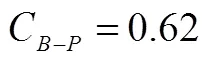
5 结论与反思

5.1 两个版本教科书概念呈现方式较为科学

该模型中，“相邻”的概念呈现方式之间差别较小（如差别仅在于所举案例的多少或者仅在于教科书中是否明确要求归纳概念等），但如果某概念的应然状态与实然状态的差距为1时，其一致度为0.5，而前述几个一致度都在0.6左右，可以说明：人教版和北师大版初中数学教科书中概念呈现方式与基于专家型教师调研的应然状态较为一致，两套版本之间的一致性也很高，这从一个侧面说明，两个版本教科书中概念呈现的设计都较为科学．这与张胜利的研究结论存在差异．张胜利对于东北地区357名初中数学教师关于数学概念的教科书呈现的调查显示：被访教师对概念呈现方式认同度分别为BSB版55%、RJB版67.5%，并认为一线教师对于教科书中概念呈现方式的认同程度不甚理想[1]．实际上两者并不矛盾，只是调查的对象与目标并不相同而已．张胜利的调研目标是一线教师对于呈现方式的认同度，也就是一线教师的实际感受，因此，其选择调查对象时需要关注对象的代表性，遴选能够代表全体东北初中教师状况的部分样本，而这里的调研是希望了解概念呈现的应然状态，两者的目标不同，自然调查对象也存在差异，这是导致结果差异的重要原因．教师对于教材具体内容理解的实然状况与教科书这部分内容的实然状况，肯定存在一定的差距，和应然状况也存在一定的差距，这样的差距，是教科书培训中需要关注的，但并不是教科书编写本身的事情，不能因为教科书理解的实然水平不高而否定教科书的编写水平，但应引起编写团队的高度重视，从培训等多个角度加强沟通，提升理解水平．

此外，对比了两套教科书中50个重要概念对应呈现方式的赋值情况，发现：其中20个概念的赋值，北师大版高于人教版；其中8个概念的赋值，人教版高于北师大版；其余22个概念，两种教材处理方式相同．相对而言，赋值高的概念呈现方式，对应的教学过程更易展开，这似乎表明，北师大版教科书更为关注概念获得的过程．

5.2 教科书可尝试引入类比建构的概念呈现方式

对一些与先前概念相似度高、学生先前学习经验丰富的概念（如二次函数、一元二次方程、分式等），教学中有教师采用类比建构的方式，调研中也有教师倡导这样的方式．如，对于二次函数，36%的专家型教师认同H（类比建构），15%的认为可以采用方式H也可以采用方式E或F．但现行教科书中都没有这样的呈现方式．在与教科书编写团队交流中，一位赞成采用该方式的编者分析了出现这种状况的一些原因，认为这些概念相对较少，采用类比建构的方式，可能与教科书原有的风格不甚一致，因此，编写组都规避了这一方式．但既然一线教师已有这样的期待，且一些概念采用类比建构的方式确实贴合学生的认知实际，建议教科书编写中，不妨选择个别概念，尝试采用这样的方式，并进行教学对比实验，基于实验状况再行完善．

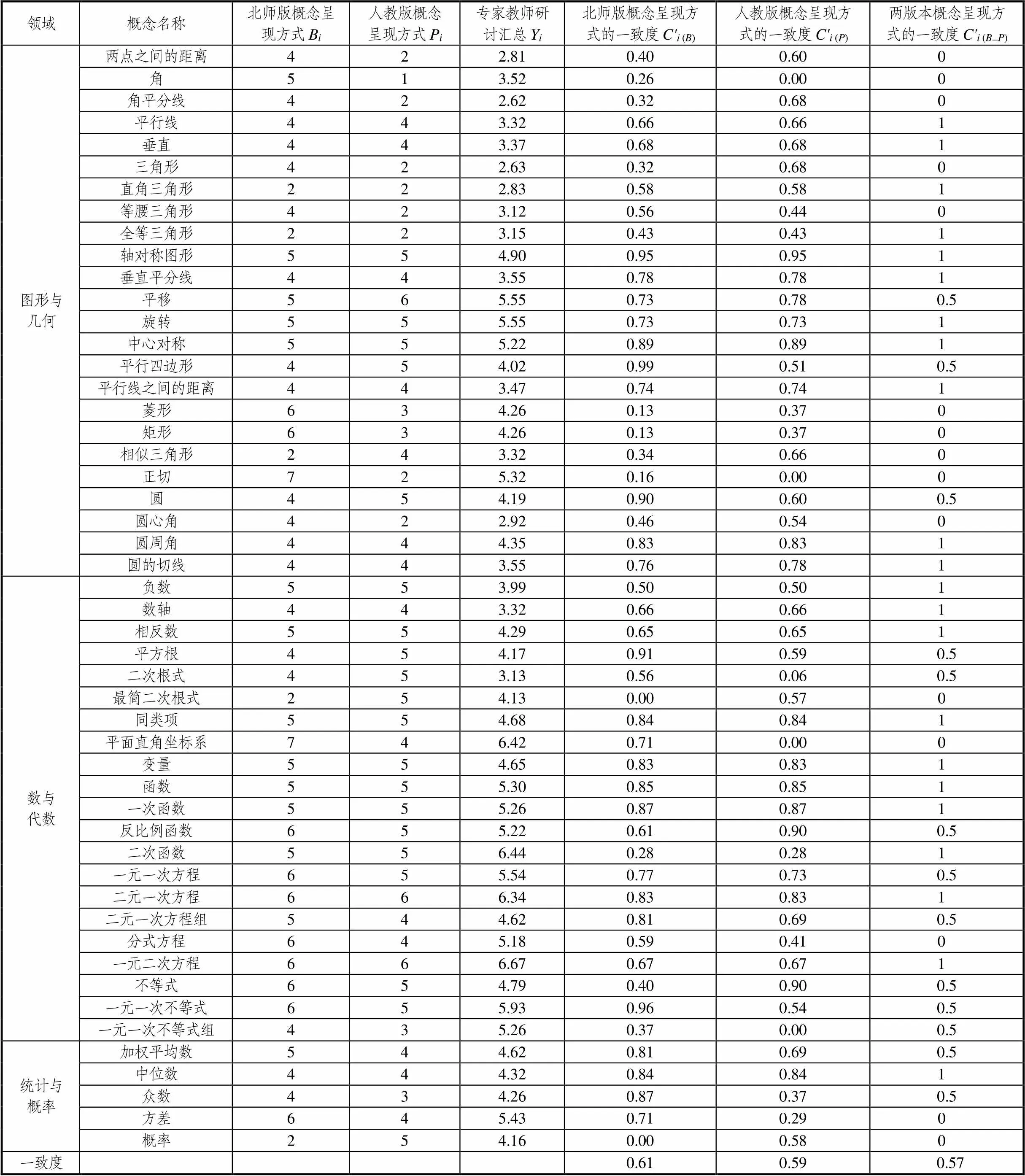
表2 50个重要概念的教科书呈现方式一致度数据

5.3 应然状态调查需遴选专家型调查对象

了解应然状态，需要调查对象有较高的判断能力，因此，务必聚焦专家型调查对象，而不能面向全体．也就是说，调查时，务必需要了解调查的目的是什么，基于这样的调查目的选择适合的调查对象，而不能遇到调查，都尝试进行较大范围的大样本随机调查．调查问卷设计时，应注意尽量不选用过于宽泛的问题，如“你认为概念呈现的方式应该如何”“你是否认同教科书中的概念呈现方式”，宽泛的问题缺乏指向性，被调查者往往很难有形成准确判断，常常出现以偏概全的现场，如对于“你是否认同教科书中的概念呈现方式”这个问题，也许教科书中某个概念的呈现与该教师的理解有明显偏差，这给教师留下了深刻印象，因而，面对该调查问题时，该教师可能就会不经意地以偏概全，从而影响到答卷的效度．调查实施时，为了达成较好的调查效果，可以采用会议调查的方式，这样可以更好地交流沟通，确保选择的有效性．总之，了解应然状况的调查，建议精心遴选调查对象，设计更为具体、更有针对性的问卷，适当的时候，可以采用会议调查，避免因对调查问题的误解而影响调查的效度．这样的调查方式，可以广泛运用到课程内容选择、教科书呈现方式设计等研究中．

总之，研究建构了一个概念呈现方式一致性的模型，并以两个版本教科书为例，进行了概念一致性研究，发现两个版本教科书概念呈现方式总体而言较为科学．后期还可以基于这一模型，进行国内外教科书的比较研究，力图获得一些国际比较的启示．也可以基于这一模型进行不同年级概念呈现方式的差异性研究，力图发现年级之间的梯度．还可以类比这一模型，进行教科书其它内容呈现方式的一致性研究．

[1] 王兄，汤服成．数学概念图式的加工机制[J]．数学教育学报，2001，10（4）：34–37．

[2] 李善良．数学概念学习中的错误分析[J]．数学教育学报，2002，11（3）：6–11．

[3] 王秀明，王家铧，李忠海．寓“理解”于数学概念[J]．数学教育学报，2005，14（2）：26–28．

[4] 吴华，周鸣．GeoGebra环境下基于APOS理论的数学概念教学研究[J]．数学教育学报，2013，22（2）：87–90．

[5] 李耀光，何小亚．新课程数学概念“螺旋式”上升编排的认知审视[J]．数学教育学报，2010，19（4）：12–14，91．

[6] 张平，彭亮，徐文彬．大陆与台湾小学数学教材中分数除法的编排比较[J]．数学教育学报，2018，27（6）：38–43．

[7] 金海月．概念图在评价数学概念性理解中的应用[J]．数学教育学报，2015，24（3）：55–59．

[8] 邵光华，章建跃．数学概念的分类、特征及其教学探讨[J]．课程·教材·教法，2009，29（7）：47–51．

[9] 章飞．数学概念的分类及度量性概念的教学思考[J]．数学教育学报，2010，19（5）：40–42．

[10] 张胜利．数学概念的教科书呈现研究——初中数学为例[D]．长春：东北师范大学，2011：1．

[11] 肖柏荣．数学概念学习的心理分析[J]．数学通报，1994，33（2）：9–10．

[12] 章飞．数学概念的分类及度量性概念的教学思考[J]．数学教育学报，2010，19（5）：40–42．

A Study on the Presentation and Consistency of Concepts in Junior High School Mathematics Textbooks

ZHANG Fei1, YU Meng-fei1, 2, GU Ji-ling2

(1. Institute of Curriculum and Teaching, Jiangsu Second Normal University, Jiangsu Nanjing 211200, China;2. College of Teacher Education, Nanjing Normal University, Jiangsu Nanjing 210097, China)

Based on combing through textbooks and communicating with the writing team, the presentation methods of concepts in textbooks was divided into four categories eight types, including concept formation, concept assimilation, and concept construction. The selection expert teachers studied all the concepts in the junior high school mathematics textbooks to obtain status of the concept presentation. This paper analyzes the concept presentation modes in the junior high school mathematics textbooks of the People’s Education Press edition and Beijing Normal University Press edition. A consistency model was constructed, with the following conclusions based on the model: The consistency of the presentation of concepts was high across the two editions. This indicates that the presentation of concepts in the two editions is generally more scientific. However, our research also shows that some concepts with high similarity to previous concepts and rich learning experiences are presented in the way expert teachers perceived, while none of the current textbooks are presented the concepts as what experts teachers perceived. Therefore, it is suggested to try to present the concept of analogical construction in textbook design.

textbook; concept; presentation mode; consistency; junior middle school mathematics

G632.0

A

1004–9894（2021）05–0021–07

章飞，俞梦飞，顾继玲．初中数学教科书中概念的呈现方式及一致性研究[J]．数学教育学报，2021，30（5）：21-27．

2021–06–10

教育部北京师范大学基础教育课程研究中心——初中数学教师理解教材及创造性使用教材的研究（1411012）

章飞（1970—），男，江苏南通人，教授，硕士生导师，主要从事课程与教学论及教师教育研究．顾继玲为本文通讯作者．

[责任编校：周学智、陈隽]