从《原本》谈中学平面几何课题式教学研究

王海青，曹广福

从《原本》谈中学平面几何课题式教学研究

王海青1，曹广福2

（1．惠州学院 数学与统计学院，广东 惠州 516007；2．广州大学 数学与信息科学学院，广东 广州 510006）

平面几何内容是中学数学的重要组成部分，也是后续立体几何与解析几何的学习基础．研究探讨了中学数学课题式教学的组织实施方式及其基本思想，梳理了欧几里得《原本》的编写特色与风格及其重要数学思想，剖析了平面几何教学内容结构与教材编排情况，在此基础上对中学平面几何模块教学内容进行课题式教学设计探索．基于对平面几何模块内容的总揽，重点探讨其中两个子课题的教学设计思路，即以“三角形内角和定理”为探究起点的课题式教学设计、凸显“勾股定理”重要价值的课题式教学设计．

《几何原本》；平面几何；课题式教学；三角形内角和；勾股定理

1 中学数学课题式教学的涵义

课题是指要研究和解决的问题，特别是一些有创新性的或前沿性的问题．撰写一份课题申报书或者完成一个课题研究常常要回答以下几个问题[1]：研究什么问题？为什么要研究这些问题，它的重要性体现在哪里？解决这些问题的关键是什么？寻求何种方法解决这些问题？这些问题的解决能给我们带来什么？因此，课题的核心就是问题，课题研究要经历发现问题与提出问题、分析问题与解决问题的科学研究过程．但大部分数学课程都已经有比较完整的理论体系，所以课题式教学与课题研究也不尽相同．课题式教学不应仅看作是按照课题研究的形式开展教学，而是教师把课程当作课题来研究，根据学科结构和知识模块“再创造”[2]教材，重组教学内容重构教学流程，引领学生围绕能揭示本质的核心问题进行探究活动，使之在经历类似于课题研究一样的活动过程中生成知识习得思想方法．

作为数学学科，教学应反映数学的本质——抽象思维模式，知识的本质——思想的载体，以及研究的本质——解决问题．中学生与高校学生的知识储备、思维水平及认知特点有较大差异，因此在中学数学课堂中实施课题式教学与高校的课程教学也会有所不同．基于此，这里将中学数学课题式教学定义为：教师基于对数学专题或模块内容整体结构与发展脉络的理解，挖掘知识产生的问题与背景并结合学生的“数学现实”重构教学，引领学生在知识的整体框架下围绕核心问题与核心概念经历发现问题与提出问题、分析问题与解决问题的过程，引发学生“再发现”数学知识及其蕴含的思想与价值，实现对教学内容的有限“再创造”．

中学数学课题式教学的内涵与理念也正反映了教育家杜威所强调的“关注学生现实生活和实践”[3]的哲学思想，并践行“教师主导学生主体”[4]的教学理念．其实质就是教师把课程当作是课题来研究进而重构教学内容，使教学过程成为“再创造”知识与思想方法的科学研究过程，这个过程突出体现以问题为内核的探究过程．这里的“再创造”是有指导的有限再创造，“数学现实”[5]是指学生的数学基础与生活实际．所以，中学数学课题式教学的实施有助于落实《普通高中数学课程标准（2017年版）》[6]提出的“四基四能”课程目标，也有助于教师和学生整体把握教学内容，促进学生数学学科核心素养连续性和阶段性发展．

数学学科的抽象性与形式化、中学数学教材的编写特点、课程标准的教学目标以及中学生的思维能力与认知水平，决定了中学数学课题式教学需遵循适当性和量力性教学原则．教学设计需结合学生的实际重构教学内容，创设恰当的、真实有效的问题以及情境驱动教学，引领学生实现对数学的有限再创造．数学在解决现实问题、科学问题和数学自身的问题中产生与发展，所以教学上提出的问题应是符合学生实际的现实问题、科学问题或数学问题．创设的教学情境根据具体知识也包括“现实情境、科学情境、数学情境”3类[6]，它们应“具有一定的生活意义、数学价值或科学价值”[7]．

2 中学数学课题式教学的组织实施方式

根据课题研究需回答的几个问题，中学数学课题式教学的设计则需相应地明确以下4个问题：产生数学知识的背后问题是什么？这些问题的重要性与教学价值体现在哪？教学中这些问题的关键和解决办法是什么？问题的解决生成哪些重要概念与原理，形成哪些重要思想与方法？实际上这就是要从数学学科结构和历史脉络出发，深入到数学内部去回答教什么、为什么教以及如何教的问题，如此才能真正有效实施中学数学课题式教学．

因此，中学数学课题式教学有赖于教师对专题或模块内容的组织与设计做充分的教学准备．教师需依据数学学科结构和数学史，像做课题一样剖析专题或模块教学内容，理清知识的来龙去脉、丰富的内涵和广泛的应用性，及其背后的精神实质和思想方法，以便向学生呈现一个能总揽专题或模块的大致轮廓．再根据知识的内在逻辑联系设计出一个个子课题，并基于对子课题的意义、地位、主要问题及解决途径的理解开展课时教学．学生则在教师引领下把学习内容当作课题一样进行研究性学习、探究性学习，经历发现问题与提出问题、分析问题与解决问题的过程，形成概念与原理，习得思想方法．

文献[1]给出了课题式教学的基本架构．同样，中学数学课题式教学组织与实施方式也强调对数学专题或模块教学内容总揽的基础上对一个个子课题进行分析研究，以问题引领和驱动具体课时内容的教学完成课题目标．中学数学课题式教学的基本流程要遵循以下3个步骤．首先，教学上先让学生对专题或模块内容的结构、知识背景及意义有一个大致的整体性认识．其次，对教学内容分解成一个个子课题，引导学生围绕问题及其情境进行探究性学习并经历类似于课题研究的科学研究过程，掌握相应的知识与方法．最后通过对一个个子课题的解决完成对专题或模块内容的整体研究达成总体教学目标，学生获得灵活的整体认知结构，不断增强实践能力，认识数学的价值，提升创新意识与数学素养，树立科学精神．需要指出的是，完成每个子课题的课时数依据其所包含的教学内容量来决定，根据教材的编排结构，每个子课题也并非一定是在连续的课时教学中完成，主要强调围绕一类核心问题沿着同一条研究主线进行．

3 中学数学课题式教学的基本思想

根据前面对中学数学课题式教学的涵义及其教学组织实施方式的探讨可知，该教学法在教材处理、教学准备与教学流程设计、教师的教学方式、学生的学习方式等方面都是在经历类似于做课题研究的科学研究过程．教师在做课题式教学研究，学生在做课题式学习研究，最终实现教师在提升自身教科研能力的同时又促进了学生学习能力与数学素养的养成．总体而言，中学数学课题式教学的实施需遵从以下6个基本的教学思想．

3.1 基于教材统整专题或模块的教学内容

实施中学数学课题式教学，教师首先要对基础教育阶段的教材结构与知识体系有完整的认知和把握，了解各个专题或模块内容在不同学段不同年级的分布情况及其教学目标与要求．基于对教材内容的整体理解才能把握相应专题或模块教学内容的结构及其知识点的联系，才能在教学设计与教学组织过程中做到承前启后、有的放矢．常言道，教师的教学不能“照本宣科”完全按照教材去教，要结合学生实际，对教材内容再创造、再组织．但这不等于“脱离教材”自立家门重新搞一套，而是要“紧扣教材”，基于教材而高于教材地用好教材，要对教材进行剖析，融入自己的理解，根据学生的情况组织教学内容．

3.2 基于数学学科结构和数学史梳理专题或模块整体架构

数学教科书根据数学的特点和编写需要，基本上按照概念的定义、定理与性质的证明、法则的推导、例题的讲解、习题的布置等顺序编排成形式化的逻辑演绎体系，而知识产生与形成的背景及问题则少有出现．这让学习者在一堆符号化的逻辑推理中很难体会到蕴含在知识背后的数学思想及其重要价值．“数学并不是按照教科书中的方式发展的”[8]，但教材不是百科全书式的科普书籍，主要是简明扼要地呈现主干知识为主．这也就需要教师基于数学的学科结构和数学史对教材内容进行再加工，理清知识产生、形成与发展的来龙去脉，及其承载的重要数学思想方法、科学家的精神品质等．从而明晰知识背景与问题本原，明确知识的教学价值及其与其它知识间的密切而丰富的联系，把握专题或模块的整体架构．

3.3 基于“先行组织者”策略呈现专题或模块的大致轮廓

美国数学教育家Ausubel所提倡的“先行组织者”[9]教学策略，是指学生正式学习某个单元知识之前，教师向他们介绍熟悉的、要比旧知识本身具有更高的抽象、概括和综合水平的，并且能使学生原有的认知结构与新知识相关联的引导性材料，为新旧知识的连接做准备．中学数学课题式教学强调学生对专题或模块内容的意义、背景与整体知识结构的认识和理解，为后续的学习提供支撑．因此，在正式开始专题或模块教学之前，教师要向学生介绍相应数学知识的背景与整体框架、主要内容与价值、主要思想与方法，它们与前后章节乃至其它学科间的联系．目的是为新的学习内容提供观念上的固着点以促进学生的学习，也为后面具体教学的问题情境创设提供预设和铺垫．

3.4 基于学生现实强调问题驱动生成新知揭示本质

中学数学课题式教学重视将具体教学内容融入到真实有效的核心问题中，并引导学生围绕问题进行探究性教学活动，这符合数学知识的形成过程．数学本身就是在解决各种各样的现实问题、科学问题和数学问题中逐步形成、发展和完善，因此以问题驱动教学是生成概念和获得原理的最佳途径．但问题及其情境需依据历史并结合学习主体——学生的现实即其数学基础和生活实际来创设，才能有效推进教学促使学生在已有知识基础上生成新知．以问题驱动教学，让学生在适当的问题情境中进行探索活动经历类似于做课题的科学研究过程，有助于他们再发现知识并深刻体验到数学概念与原理背后所蕴含的思想方法，感受到数学的价值、作用与魅力．

3.5 基于高观点视角指导核心概念与原理的教学

高等数学的知识体系与思想观点对初等数学教学具有高屋建瓴的指导作用．教师若能从高等数学的视角审视初等数学的知识，将有助于更好地理解教学内容以整体设计教学和对关键问题的把握、变式与引申．正如德国数学家F. Klein所言：只有观点高了，事物才能显得明了而简单[10]．事实上，高等数学是在初等数学的基础上发展而来，初等数学的许多知识是高等数学的特殊情形．所以，中学数学中有些重要的概念和性质、定理、法则需要站在高等数学的高度，从数学的学科结构出发去认识才能揭示其本质，这有利于设计课题研究式的教学过程，有利于突破教学重点、分解教学难点．

3.6 基于全体学生注重适度弹性教学设计

《普通高中数学课程标准（2017年版）》[6]与《全日制义务教育数学课程标准（2011年版）》[11]指出基础教育数学课程“应面向全体学生，人人都能获得良好的数学教育，不同的人在数学上得到不断的发展”．所以，教学设计应具备一定的弹性，既面向全体学生也关注学有余力学生的需要．但数学教材的编写是立足于中国各地区全体学生的共同需要，考虑学生和教学环境的共性．而每一位教师面对的是各自地区具有不同特性的学生，教师需基于教材结合学生实际组织教学内容．“课题式教学不仅回归了教育的本质，而且极大增强了课堂的弹性．”[1]显然，课题式教学在弹性教学设计上有着天然的优势，它自带课题研究的基因，基于某一问题的课题研究的深度与广度可以根据实际需要来确定．

4 中学数学课题式教学案例研究

结合中学数学课题式教学的涵义、组织实施方式与基本思想，下面以中学平面几何模块内容为例探讨相应的课题式教学设计．

4.1 《原本》特色与思想对平面几何教学的启示

中国现行的中小学数学教材内容，除了近现代的向量、概率统计、微积分等，其中算术、代数、几何与三角的内容几乎都来自古希腊时期欧几里得的《原本》．因此，了解《原本》的编写风格与特色、涉及的主要数学思想，有助于教师整体把握中学数学内容进行有效的教学设计．《原本》是历史上最早的一本以公理化方法组织数学内容的书籍，全书13篇集结了希腊古典时期数学家工作的精华，涉及平面几何、立体几何、比例论、相似性、数论、不可公度量等，其中8篇论述了平面几何与立体几何的相关定理与性质．书中主要体现了归纳猜想、演绎推理、分类讨论、数形结合、归谬穷竭、等积变换等思想方法．

举个例子，毕达哥拉斯定理也就是中国的勾股定理，史学家们认为是欧几里得在《原本》中对该定理给出了第一个严谨的推理证明，而毕达哥拉斯学派可能是在实际的测量中根据许多特例归纳得出直角三角形3边关系，并没有给出严格的证明[12]．假设直角三角形中，∠=90°，=，=，=，要证明等式2+2=2成立．按照当时数学家处理代数式子的思路，很自然地考虑将这个等式转化为几何问题来解决，也自然地将2、2、2看作是3个正方形的面积．所以欧几里得构造了如图1所示的几何图形，再利用全等三角形的性质和等积变换的思想证明得到两个小正方形的面积之和等于大正方形的面积，即2+2=2．整个证明过程充分体现了将代数问题转化为几何问题的数形结合思想，将线段的长度问题转化为平面图形面积问题的一维向二维转化的思想，等面积变换的思想．

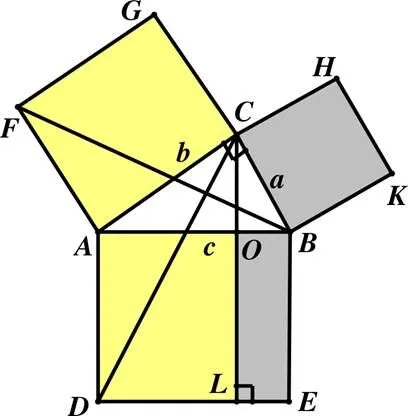
图1 几何图形的构造

毕达哥拉斯定理证明所涉及的转化与化归、等积变换与数形结合的数学思想方法贯穿整个中学数学的教学，这也正是毕达哥拉斯定理在中学阶段具有举足轻重地位的重要原因．同样的方式，《原本》对完全平方公式(±)2=2±2+2与平方差公式2–2=(+)(–)的证明就是构造相应矩形和正方形的面积给予几何证明（如图2、图3），正如现在中学教材里给出的直观几何解释一样．这些在今天看起来不算严谨的证明在古希腊时期是没有问题的，因为当时还没有出现负数．

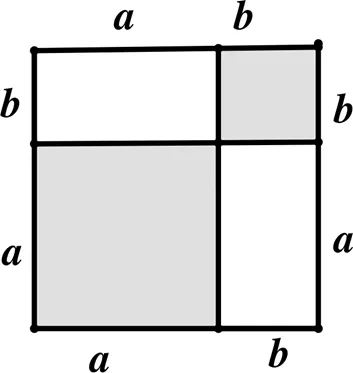
图2 图形的面积（一）

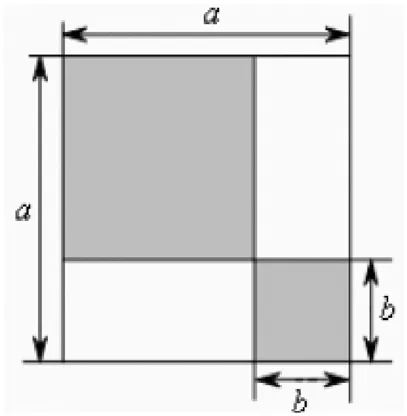
图3 图形的面积（二）

三角学则在亚历山大时期由于天文学和航海技术发展的需要得以创立和发展．数学家托勒密（约90年—168年）在其著作《大汇编》中给出了第一个三角函数表[12]．古希腊及其后来的阿拉伯数学家主要研究的是球面三角，直到1450年后，由于测量的需要，平面三角的研究才愈加受到重视．阿拉伯人阿尔比鲁尼（978—1048）给出了平面三角形的正弦定理，法国数学家韦达（1540—1603年）在1593年给出了平面三角形的余弦定理．随着数学自身的发展，平面中的正、余弦定理被推广到维欧氏空间中得到高维正、余弦定理的形式．《大汇编》中也给出了著名的托勒密定理，定理内容为：圆内接凸四边形两对对边乘积的和等于两条对角线的乘积．即如图4，四边形是圆的内接四边形，则有·+·=·，这个定理与正、余弦定理及一些三角恒等式有着密切联系．

图4 四边形的对角线

数学史清晰地反映出数学始于问题．《原本》的内容组织、证明风格特点则突出体现了重要性质定理的证明及推导中所蕴含的数形结合、转化与化归、特殊与一般、分类讨论、类比联想、等积变换等数学思想．通过这些思想将相关知识密切联系起来，由浅入深、层层递进，不断引出新的结论．因此，中学数学教材内容中的各个知识点间也有着丰富的联系，彼此关联形成有机整体，其蕴含的数学思想就是它们之间的重要连接点，教学组织与实施应通过问题揭示知识间的内在联系．

4.2 新课程教材中平面几何的整体知识体系

新课程的改革不仅要求教师更新教学理念改进教学方式，教材内容的编写与组织也发生了巨变．在新课程改革之前，中学数学教材的体系是代数、几何、三角分支各自独立、自成一册，结构体系整体呈现．基础教育数学新课程标准下的教材结构体系由集中走向分散，各个模块内容由独立走向融合，出现在不同年级的教材中．打破数学各分支结构的界限统整为综合数学有助于知识的整合，也符合学生螺旋式上升的认知特点，但同时也给学生整体理解和把握各模块的知识体系结构带来一定的障碍．强调对模块知识结构、价值与意义总揽的中学数学课题式教学有助于去除这一屏障．教师在开展某一专题或模块的课题式教学之前，首先要向学生呈现将要学习内容的背景与整体知识结构、新旧知识间的联系、重要价值与主要思想方法．

平面几何模块的内容分布在小学、初中、高中3个学段，主要集中在初中阶段．解三角形有一部分内容如正弦定理、余弦定理安排在高中，小学部分的平面几何内容主要是让学生对一些基本图形有直观感性的认识，会做简单的运算．中学阶段的平面几何整体知识框架如图5，包含了几何变换、三角形、四边形、圆及其综合应用问题．相应的性质与判定即为互逆命题，两者逻辑关系密切．正如前面对《原本》的分析一样，平面几何的教材内容蕴含了分类讨论、特殊与一般、数形结合、转化与化归、类比联想、等积变换等重要数学思想．从教材编排的整体结构看，对不同三角形、四边形的讨论涉及到分类讨论的思想，从全等三角形到相似三角形的研究属于特殊到一般，从一般的四边形到特殊四边形的探讨属于一般到特殊，在讨论具体的性质、判定时则突出体现了数形结合、转化与化归、类比联想、等积变换等思想．

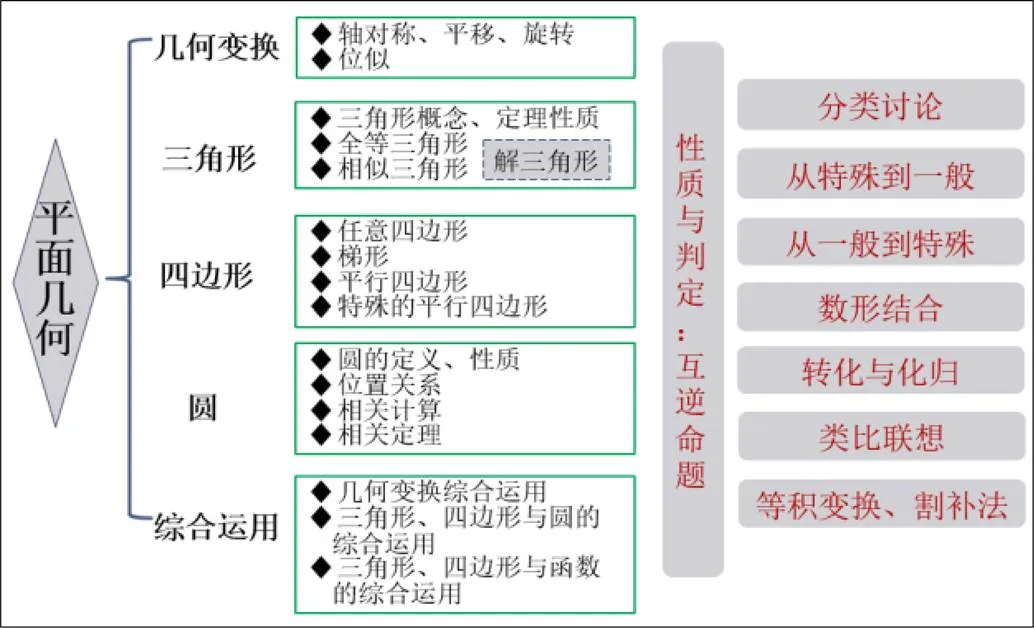
图5 平面几何知识框架

在开始平面几何模块内容学习前，教师先大致介绍这个模块内容的整体结构、涉及的主要思想方法、重要的价值及其在实际生活中的应用等，让学生对知识的整体轮廓有基本的认知，为新的学习内容提供预设和铺垫，建立支架与固着点．这同时也能缓解学生“为什么要学”的困惑，在情感上获得意义学习的心向．类似地，在进入到具体单元的学习前，教师也应向学生介绍相应单元的整体知识结构，让学生了解单元的基本概貌．而当一个单元学习结束，教师则需引导学生复习本单元的知识点及其重要思想、主要的题型与方法，对其进行归纳总结，逐步形成比单元之初的概貌更为具体、完善和丰富的整体知识结构图．同样地，当平面几何模块内容学习完毕，教师也需引导学生进行类似的复习活动．

4.3 平面几何模块课题式教学的两条研究主线

学生对平面几何知识结构有了基本了解和认识后，教师接下来需根据模块内容的内在逻辑关系分解成数个有机联系的子课题进行课题式教学．每个子课题的教学根据其内容的多少安排一定数量的课时来完成，有些子课题可以在连续的几个课时中完成，有些则根据教材内容的分布和难度需要经历一定的时间跨度来完成．

根据前面对平面几何模块知识结构和教材编排的分析，子课题的设计可分为体现“一般与特殊”以及“类比联想”思想的四边形单元、全等三角形与相似三角形单元的教学，反映“互逆关系”的相应性质与判定定理的教学，突出“知识联系、思想迁移”的围绕一系列知识点展开探究的教学．需说明的是这些子课题之间并不是相互独立而是彼此交错互为实现的关系．下面着重谈以“三角形内角和定理”“勾股定理”为中心围绕一系列相关知识点展开探究教学的课题式教学设计．

（1）以“三角形内角和定理”为探究起点的课题式教学设计．

四年级下册已经出现过“三角形内角和定理”教学内容，主要是让学生以“量、拼、折”动手操作的方式直观了解“三角形内角和为180°”这个事实，也为八年级上册进一步学习这个结论的严格证明过程作铺垫．因为在“量、拼、折”中就包含着证明的方法与辅助线的作法，八年级的教学可以在这一基础上引出对新知的探究．根据知识生成原则，也可以利用学生已有的知识经验“长方形的四个角都是直角”以及平行线的性质来探讨“三角形内角和定理”的教学．由三角形的内角和、外角和可以在平面内推广到对一般多边形的内角和与外角和、曲边形方向改变量的探讨，而从平面类比到空间可以推广到空间多面体平面角的和与多面角截面上闭折线的方向改变量之和等相关内容的讨论．这个过程涉及特殊到一般、化未知为已知、类比联想、不变性等重要数学思想．三角形内角和定理与相关知识点的联系如图6，这是教师要掌握的整体知识结构，结合学生实际再进行具有一定弹性的教学设计．正如F. Klein所言，教师掌握的知识要比他所教的多得多，才能引导学生绕过悬岩，渡过险滩[10]．

图6 三角形内角和定理与相关知识点

面向学生的课堂教学，教师在整体理解知识和了解学生的基础上，则可以按下面思路进行课题式教学设计，如图7．虚箭头部分表示相应的内容为拓展性知识，教师结合教学和学生实际情况进行弹性设计，为学有余力学生提供更广阔的学习空间．

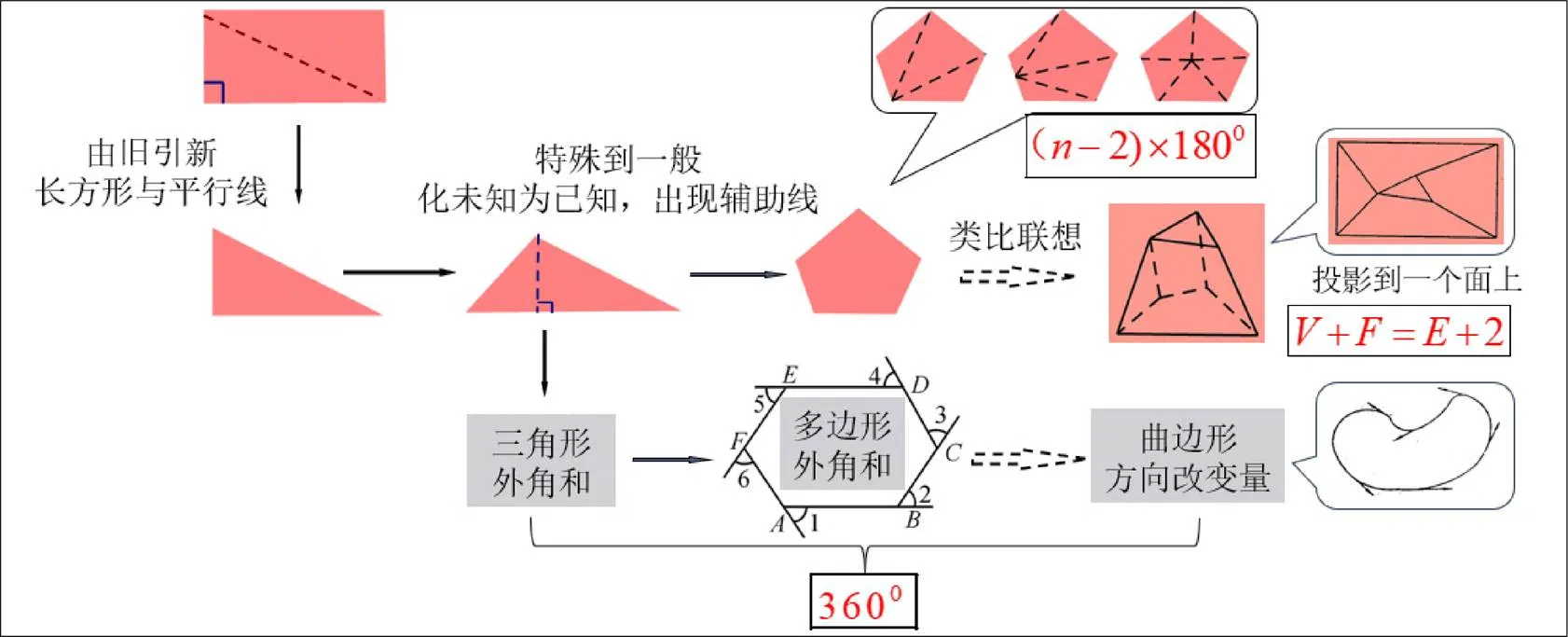
图7 课题式教学设计思路

回顾“长方形的4个角都是直角”知其内角和为360°，然后向学生提出问题1：多边形中最简单的图形是三角形，三角形中最特殊的是直角三角形，请问直角三角形的内角和是多少？你能用长方形的内角和为360°来证明它吗？从长方形到直角三角形自然引出辅助线将长方形分割为两个直角三角形，再运用平行线的性质可以证明直角三角形的内角和为180°．接着提出问题2：对于一般的三角形，这个结论是否依然成立呢？该如何证明？问题2本身就蕴含了从特殊向一般过渡的思想，而要解决这个一般性问题，需引导学生化未知为已知，回到直角三角形的结论，由此作辅助线将一般三角形分割为两个直角三角形来计算相应的内角和．

同样地，引导学生由特殊到一般提出问题3：三角形是最特殊的多边形，一般多边形的内角和又怎么计算呢？再次经历化未知为已知的探究过程，将多边形分割转化为三角形来进行计算，得到多边形的内角和为(–2)×180°，只与边数有关．从长方形到直角三角形，再到一般的三角形、多边形，都是在平面内从特殊到一般一步步地进行推广探索，为了解决提出的新问题，又反过来从一般到特殊，将未知问题转化为已知结论来进行处理，这个过程中几何教学的重点与难点——“辅助线”就自然而然地根据需要出现了．

也可以将问题从平面推广到空间进行探索，通过类比联想提出问题4：在3维空间中，多面体平面角的和又是多少呢？假设多面体的顶点数为，面数为，边数为，计算多面体平面角之和的直接方法是利用多边形内角和公式求出每个面的内角和再相加．也可以利用三视图的知识将问题从空间转化过渡到平面上来处理．将多面体投影到一个平面上，投影只改变多面体各条边的长度而不影响各个面的边数，因此多面体平面角的和等于投影到平面上的各个多边形的内角之和．在这个探究过程中会得到著名的欧拉多面体定理：+=+2，2称为欧拉示范性系数，是一个重要的不变量，不同的欧拉示范性系数代表不同的多面体类型，2对应的是简单多面体．对于问题4，这里体现了教学设计的弹性，并不要求所有学生都要经历这个探究过程．教师应结合学生的实际来考虑是否需要在解决前面3个问题的基础上进一步拓展引申，或作为阅读材料向学生介绍空间中的探究情形．

另外一个方向，是从三角形的内角和过渡到三角形的外角和．教材将三角形的外角和定理看作是三角形内角和定理的一个推论，事实上“三角形的外角和为360°”要比“三角形的内角和为180°”这个结论更为本质．因为进一步推广发现“多边形的外角和也是360°”，它跟多边形的边数即形状没有关系，也可以看作是一个不变量．这个方向的教学过程既要重点运用旧知推导新知，也要通过动态证明一个物体沿着多边形的边运动回到起点刚好转了一周，突出多边形的不变性揭示本质．同样，一个封闭的曲边形的方向改变量同样是360°．在初中除了圆，没有涉及曲边形的相关内容，教师可根据实际情况考虑作为数学阅读材料供学有余力且有兴趣的学生了解学习．

（2）凸显“勾股定理”重要价值的课题式教学设计．

从前面对《原本》的分析可以发现，勾股定理的重要价值之一在于其证明过程中涉及的数学思想方法，这些思想方法贯穿初中几何乃至代数内容的教学，并与平方差公式、完全平方公式、中位线定理、正弦定理、余弦定理、基本不等式等知识点有着直接的联系，也与著名的费马大定理和托勒密定理相关，如图8．可将这些知识点形成有机整体进行课题式教学设计，突出知识间思想方法的迁移．

图8 勾股定理与其它定理的相关性

由于勾股定理的发现与证明时间不同步，这使得要引领学生自然发现定理成为教学上的难点，且欧几里得的证明对初中学生来说也有一定难度．为了解决这个难点，可以充分运用古代中国数学家的智慧．古人特别热衷于对尺规作图相关问题的探讨，比如大家熟悉的“三大作图不能问题”等，由此也衍生出很多的数学结论．《九章算术》是中国古代的经典数学著作，其第一章“方田”[13]就专门介绍了出入相补原理及其应用．出入相补原理也称割补术，是对等积变换思想的运用．所以，不管是在古希腊还是在古代中国，面积法的使用都非常广泛．

正方形在尺规作图、面积计算等问题中起着至关重要的作用，因为多边形可以分割成三角形，三角形则可转化为等积的矩形，而矩形又可以利用直角三角形的射影定理转化为等积的正方形，即“方出于矩”．将三角形变为等积矩形的过程中就隐含着三角形中位线定理及其证明过程．所以在古代中国，勾股定理的证明很可能也是在处理尺规问题时偶然发现的．如作一个正方形，其面积为两个已知正方形的面积之和，这个问题的解答对应于刘徽的“青朱出入图”，详见图9．如果问题中的两个正方形变为两个全等矩形，构造出的正方形就是“赵爽弦图”，如图10．“青朱出入图”与“赵爽弦图”是对勾股定理的直观证明．

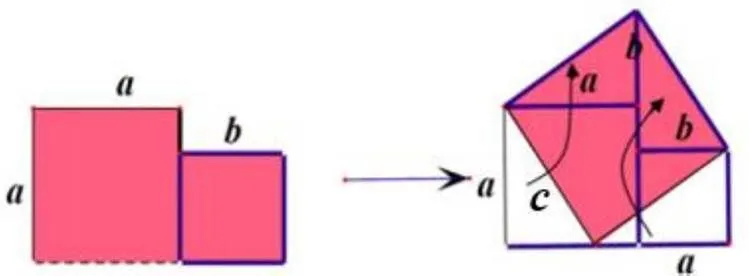
图9 “青朱出入图”模型

图10 “赵爽弦图”的构造

因此，勾股定理的教学可以结合实际先提出学生力所能及的问题I：如何作一个大正方形，其面积为两个大小相同的正方形面积之和？这是大部分学生可以解决的问题，如图11，并引导学生归纳总结问题I的作图构造方式、结论与规律．进一步地，提出更一般性问题II：如何作一个大正方形，其面积为两个大小不同的正方形面积之和？在解决问题I的基础上引导学生在大正方形的底边选择合适的点构造全等三角形来处理，即如图9．进一步归纳总结在等积变换过程中所体现的两个已知正方形边长与大正方形边长的关系，即为：2+2=2，得证．然后向学生介绍欧几里得的证明方法，突出体现两者在证明过程中思想方法的统一性和东西方文化的差异性．古希腊人追求演绎推理而中国古代数学则崇尚实用和算法，在证明中也反映出了这两种不同风格的数学文化精神．更为详细的关于勾股定理的教学设计可以参考文献[14]．

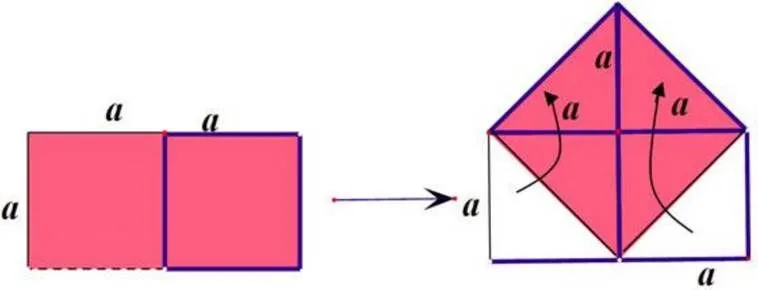
图11 正方形的面积

教学还可以结合学生实际提出拓展性问题III：直角三角形的两直角边、的平方和等于斜边的平方，即2+2=2．若边、所夹的角为锐角或钝角，3边的平方和又满足什么关系呢？当然，利用高中的余弦定理很容易判断得出结论，但运用初中学生已有的知识基础也可以解决这个问题．如图12，在直角三角形中，以点为圆心，直角边、为半径作圆，构造两边分别等于、的锐角三角形和钝角三角形并使得第三边与边平行，可直观得到：钝角三角形中2+2>2，锐角三角形中2+2<2．教师还可以考虑给学生关于费马大定理的相关阅读思考材料，体会特殊到一般的数学思想应用，感受数学家孜孜不倦追求严谨的科学研究精神．问题III和费马大定理阅读材料作为拓展性内容不对教学作硬性要求，教师结合实际进行处理．这两个内容的目的是要培养学生的发散思维能力，学会运用数学思想方法对原有的问题与结论进行拓展引申和深入思考探究，体会数学知识之间的密切联系性．

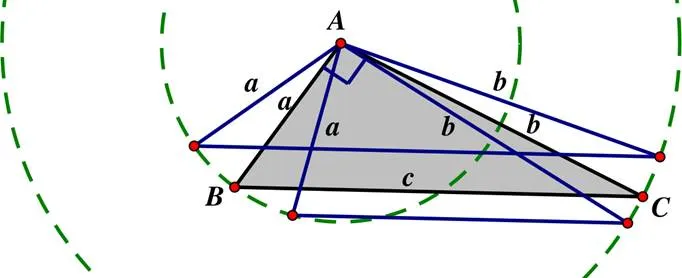
图12 三角形的边角关系

对于平方差公式与完全平方公式的教学，教师在引导学生完成两个公式的代数归纳与推导证明的基础上，应启发学生观察公式中各项所代表的几何意义并尝试构造出相应的几何图形（如图2、图3），将符号化的代数式子转译为直观化的几何图式，渗透数形结合的思想．而三角形中位线定理的教学可以顺着勾股定理的教学思想向学生提出问题IV：如何将一个三角形转化为等积的矩形？有两个解决问题的方向，一是保持三角形的高不变，使底边长为原来的一半；二是保持三角形的底边长不变，使高变为原来的一半，如图13．引导学生在解决问题的过程中自然引出辅助线并发现三角形的中位线定理，再次体会等积变换的思想．

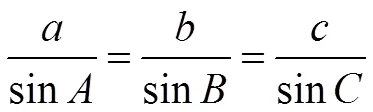
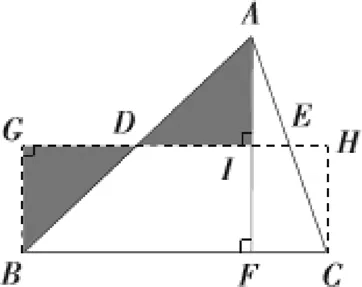
图13 三角形与矩形的转化

图14 直角三角形的高

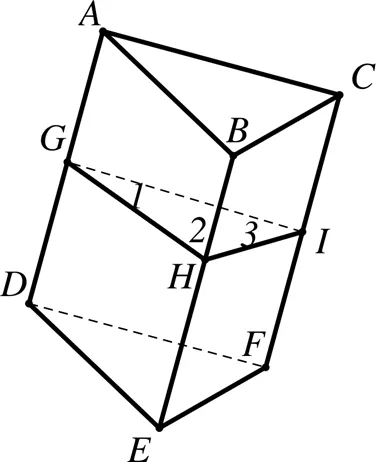
图15 斜三棱柱

综上有，以“勾股定理”为中心的课题式教学设计思路框架如图16．同样，虚箭头部分为拓展性内容，教师应根据实际进行弹性教学组织与设计．

图16 课题式教学设计思路框架

4.4 回顾与反思

通过对平面几何的历史与教材内容的剖析，可以清晰地看到数学知识间是一个相互密切联系的有机整体，教学应该突出知识间的重要连接点，以便于学生形成良好的认知结构．特别地，教学应注重在旧知的基础上灵活运用相应的数学思想方法探寻新知的生长点，引发学生对新知的探究．教师引领学生在探究活动中习得概念与原理、体会蕴含其中的数学思想方法，同时也要启发学生尝试运用数学思想方法提出问题进行探究学习．如运用特殊到一般、类比联想（从低维到高维，从有限到无限，由直到曲）可以将原有的问题进行拓展引申和推广，运用转化与化归思想可以化未知为已知、化不规则图形为规则图形，这个过程自然地引出辅助线解决了几何教学的难点．还有重要的分类讨论、数形结合等数学思想的运用[16–26]．

此外也可以发现，初等数学的许多结论是高等数学中的特例，高等数学的某些结论是初等数学的一般化．从高等数学的视角解读初等数学相关知识有助于教师更好地把握知识的整体结构进行恰当的教学设计．事实上，初等数学与高等数学的本质区别不在于使用不同的思想方法、方式研究问题，而在于数学思维的抽象程度、知识的形式化程度不一样．因此，数学教学过程应该是一个像数学家一样进行数学研究的过程，在经历发现问题与提出问题、分析问题与解决问题的过程中习得数学思想方法和处理问题的思维方式．

[1] 曹广福，刘丹．课题式教学法探析[J]．数学教育学报，2020，29（3）：32–36．

[2] 弗赖登塔尔．作为教育任务的数学[M]．陈昌平，唐瑞芬，译．上海：上海教育出版社，1995：110–111．

[3] 杨旭，李剑萍．文化契合性：杜威教育理论在中国传播流行的深层原因[J]．教育科学研究，2019（3）：82–87．

[4] 季丹枫，杨轶文．正确认识教师在教学中的主导作用[J]．基础教育研究，2019（2）：8–11．

[5] 弗赖登塔尔．数学教育再探[M]．陈昌平，唐瑞芬，译．上海：上海教育出版社，1999：74．

[6] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：2–82．

[7] 曹广福，张蜀青．论数学课堂教学与评价的核心要素——以高中导数概念课为例[J]．数学教育学报，2016，25（4）：17–20．

[8] 邓纳姆．微积分的历程——从牛顿到勒贝格[M]．李伯民，王军，张怀勇，译．北京：人民邮电出版社，2010：14．

[9] 施良方．学习论[M]．北京：人民教育出版社，2001：237–239．

[10] 菲利克斯•克莱茵．高观点下的初等数学（第一册）[M]．舒湘芹，译．上海：复旦大学出版社，2015：2–4．

[11] 中华人民共和国教育部．全日制义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：2．

[12] 莫里斯·克莱因．古今数学思想（第一册）[M]．张理京，译．上海：上海科学技术出版社，2014：27，53，101．

[13] 徐品方．白话九章算术[M]．成都：成都时代出版社，2002：37．

[14] 王海青，曹广福．基于整体理解的“勾股定理”教学再探[J]．数学教育学报，2018，27（5）：37–41．

[15] 王海青．数学史视角下“正弦定理”和“余弦定理”的教学设想[J]．教学与管理，2017（10）：67–69．

[16] 严卿，喻平．初中生逻辑推理能力的现状调查[J]．数学教育学报，2021，30（1）：49-53．

[17] 李杰民，廖运章．条件概率的本质及其教学建议[J]．数学教育学报，2021，30（1）：54-60．

[18] 邓海英，严卿，魏亚楠．数学情境问题解决错误分析与评价[J]．数学教育学报，2021，30（1）：61-67．

[19] 马淑杰，张景斌．高中学生数学原有知识水平和学习认知负荷对数学课堂学习效率的影响研究[J]．数学教育学报，2021，30（2）：26-31．

[20] 伍春兰．PDSA视域下基于教师学习的中学数学课例研修研究[J]．数学教育学报，2021，30（3）：78-82．

[21] 栗小妮，汪晓勤．HPM课例研究对教师MKT的影响[J]．数学教育学报，2021，30（3）：83-89．

[22] 李让美，郭衎，曹一鸣．学生合作问题解决过程中的教师注意——基于15位职前数学教师的眼动研究[J]．数学教育学报，2021，30（2）：42-47．

[23] 赵思林，潘超．中学数学教师核心素养及构成要素[J]．数学教育学报，2021，30（2）：48-54．

[24] 陆珺，胡晴颖．论数学解题教学的教学[J]．数学教育学报，2021，30（2）：55-60．

[25] 路江江，王亚妮．高中数学教育中如何培养学生的数学核心素养——王尚志教授访谈录[J]．数学教育学报，2021，30（2）：67-70．

[26] 马勇军，王童．近十年中国中小学数学教育研究范式的回顾与展望——基于人大复印资料的内容分析[J]．数学教育学报，2021，30（2）：90-96．

On Project-Based Instruction of Plane Geometry in Middle School Based on

WANG Hai-qing1, CAO Guang-fu2

(1. School of Mathematics & Statistics, Huizhou University, Guangdong Huizhou 516007, China;2. School of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China)

Plane geometry is not only an important part of middle school mathematics, but also the basis of subsequent solid geometry and analytic geometry. This paper discusses organization and implementation of project-based mathematics instruction in middle school, combs writing characteristics and style of Euclid’sand its important mathematical thought, analyzes structure of plane geometry’s teaching content and arrangement of teaching materials. Then research explores project-based instruction to plane geometry in middle school. Based on overview of content of plane geometry, this paper mainly discusses design ideas of two subtopics. That is, the project-based instruction design with “triangle interior angle theorem” as starting point, and the project-based instruction design highlighting important value of “Pythagorean theorem”.

; plane geometry; project-based instruction; triangle interior angle theorem; Pythagorean Theorem

2021–07–24

广东省教育科学“十三五”规划2020年度研究项目——新师范背景下“U—G—S”校地数学教师教育共同体的构建及其运行机制探索（2020GXJK410）；广东省本科高校高等教育教学改革项目——课程思政融入数学学科教育课程的教学探索与实践（2020年）；广东省教育研究院2019年教育研究项目——“U—G—S”协同机制下数学教师职前培养与职后培训一体化建设研究（GDJY-2020-A-s150）

王海青（1978—），女，广东河源人，副教授，博士，主要从事数学史与数学课堂教学研究．

G632.4

A

1004–9894（2021）05–0039–08

王海青，曹广福．从《原本》谈中学平面几何课题式教学研究[J]．数学教育学报，2021，30（5）：39-46．

[责任编校：陈汉君、陈隽]