基于学术史的民国时期数学学习心理研究

杨 帆，代 钦

基于学术史的民国时期数学学习心理研究

杨 帆，代 钦

（内蒙古师范大学 科学技术史研究院，内蒙古 呼和浩特 010022）

清末民国初期西方心理学著作逐渐被引入中国，西方数学心理学研究成果也随之被引进，中国数学教育研究者们在学习和吸收的基础上开展了数学学习心理学的研究，主要内容包括算术学习心理、代数学习心理、几何学习心理3个方面．四则运算是算术学习的主要部分，练习的形式和时间分配影响算术学习的效率．算术是经验抽象，代数是表记抽象，在一些问题中，代数方法比算术方法更为简便，表现出的代数能力较为明显．当时的研究者们认为几何学习需要心理过程复杂程度高于代数和算术．

民国时期；数学学习心理；算术心理；代数心理；几何心理

民国时期算学（即数学，1922年至1939年称算学，1939年以后称为数学）学习心理研究不是从中国古代心理学基础上衍生出来的，而是从欧美国家引进的．民国时期是一个吸收西方数学学习心理知识并在中国实践和发展的重要时期，其中算学学习心理理论对现在的数学学习心理研究具有补充和指导作用．截止目前，尚未发现关于民国时期算学学习心理的研究，研究者对民国时期算学中的数、算术、代数、几何学习心理相关内容进行阐述，希望引发更多研究者关注．

1 问题之缘起

如何学习数、算术、代数、几何之间的对话，怎样改进数学教育的不良，学生为完成数学作业而埋头伏案，平时用功，但成绩却不佳的原因，一直都是数学教育研究的重要课题．数学教学效果的优劣取决于数学教学方法的合理性和学生学习的主动性，而学习和教学方法又以数学学习心理为基础．因此，一直以来，数学学习心理研究处于数学教育的重要位置．民国时期研究者们也已经关注到这些问题，其研究重点表现出由学习国外相关文献逐渐地向结合国情、自主地研究数学学习心理过程转移的特点．算学学习心理学研究文献有两种：其一为翻译论著，其二为国人编著的论著．国人编著的算学学习心理论著主要以国外相关算学心理实验为依据，以实验结果为指导，从学生学习算学具体内容的心理发展变化的角度进行研究．在例题讲解上，则主要选取于中国算学教科书中的题作为剖析对象，便于研究者与一线教育者的理解应用．民国时期算学学习心理文献的研究内容虽然零散，但主要研究内容有：算术、代数、几何的学习心理，这与现在的数学学习内容是一脉相承的，也是研究者以数的学习心理、算术学习心理、代数学习心理、几何学习心理作为分类标准进行阐述的原因之一．民国时期算学学习心理学研究文献数量有限，算术学习心理研究的文献最多，几何的研究文献数量少于代数，其中，中国现代教育心理学家艾伟、汤鸿翥的论著较多．

一切数学学习都具有某种共同的过程，不管精神作用如何，构成有效数学学习的心理过程总是按照某种根本上相似的法则构成．如果数学教育不根据学习者的心理特点而改弦更张，运用教学方法而不在根本上谋补救，危险殊甚．

2 数概念的认识

数是算学心理研究的基本依据，同时数具有的意义为算学学习的内容扩充提供了更多可能性．学习者如何理解数、数与聊念（类似于现在的联想）、数的学习心理过程一直备受研究者们的关注．杜威（Dewey）、桑代克（Edward Lee Thorndike）、罗素（Russell）等人对此提出了自己的观点，他们的这些思想观点，在民国期间传入中国并产生影响．

2.1 数概念之界定

数是社会演化的产物，对数概念的认识和界定是一个极为复杂的过程，自古希腊毕达哥拉斯开始讨论数概念及其特征以来，各个历史时期对数概念的界定说法不一．20世纪，西方哲学家和教育家们更关注数概念的研究，并提出了各自的观点．美国实用主义哲学家和教育家杜威指出：“数为一定量之重复，此一定之量用作量法单位，以等于或表示同质量为比较值．”[1]英国哲学家、数学家罗素认为：“数为一种方法，用以汇集一定具有条件之积，数为人和物用以代表某类之数．”[2]美国心理学家和教育家桑代克主张数的目的意义有4种：第一种为序列的意义，也叫排列的意义，如1、2、3等；第二种为一个数目是几个单位的集合，是汇集一定之积（聚合，collection）的一种方法，如5包括5个单位，是由5个1集成的，第二种意义与罗素对数的界定在本质上是一致的；第三种是比量的意义；第四种是相关的意义，即一个数目与其它数目之间的关系，如七比八小、二乘以四为八，彼此相关，四则运算即为数目之间的相关．桑代克更多的是站在学习者的立场界定数的概念，比杜威和罗素更具体、更有可操作性．杜威、罗素、桑代克的这种界定与古希腊毕达哥拉斯学派的界定基本相同，毕达哥拉斯学派认为宇宙间的一切现象都能归结为整数或整数之比，“1”是一个不可分割的单位，若干单位的不同组合形成不同的正整数[3]．

2.2 数的学习心理

通过具体的实物和经验，人类开始接触并了解数．如人的10根手指对十进制系统的发展颇有贡献，后来发现手指以外的单位，即石子（拉丁文，Cac ulus）是计数的单位，因为石子可以表示比手指多的数．随后用不同的方法逐渐了解数可表示抽象的事物．学习者如果能够正确理解数及表示出数之间的相互关系的符号，对进一步学习算学及解决问题时需要的推理与归纳能力有较大的帮助．正如英国数学家和教育家怀特海（Alfred North Whitehead）所言：“一种新的、独特的能力，即使用符号的能力．”[4]民国时期，研究者们普遍认为儿童接触数目的机会大致有3种：普通计数法、普通分组法、普通测量法．测量（measurement）的目的在于用一定的单位测量一种事物的数量．如数目“1”非固定的东西，可视作一种标准的单位（standard unit），用其测量较大的全体[5]．在一切测量方法中最抽象的是货币，因为货币是测量价值的标准．食物和兽皮的直接价格因人交往频繁会发生变化，此后商业兴起，价值观念开始离开实物，而以新方法取而代之，即一种抽象观念再加一种抽象观念，使其思想与心理更加复杂．

数为抽象名词，非感官事实[1]．常说的现有五六个成年人，儿童有七八个，成年人和儿童非数，均可通过视觉、听觉和触觉等感受到，那么五、六、七、八在哪里呢？古人以温饱为业，毕达哥拉斯提出数的概念之前，虽无明确的数的定义，但数与量却存在，如度量长短有尺寸等．儿童在呀呀学语时，无意识中就已会说八、六等数字，但此时的数无秩序（次第series）且不能连贯，与前面提到的桑代克提出的数的第二种意义序列相对应．随着数量增多，则用“几个”或“许多”表示多数．这和现在所说的“数感”大致相同，是一种抽象（abstraction）过程．抽象是思维过程的一种，与具体化相对，人在分析、综合和比较的基础上抽取同类事物具有的本质特征，舍弃个别的、非本质特征的思维过程[6]．关于分析能力与抽象的关系，分析能力越大，则抽象的作用越大，反之，随着抽象能力的提高，分析能力亦提高．民国时期学生在学习过程中常出现分不清抽象的数和具体实物的问题．例如：

学习者错误在于不知道这里的数为抽象名词，与物混淆，二十七为男生人数，而不是男生，十五代表女生人数，不是女生[1]．以此例为鉴，教师如果因为忽视数的抽象而不教是大误，一切数或量都要依赖于此抽象作用．

数学本身就是抽象思维的学科．数是一种抽象的工具．民国时期的研究者们已经意识到数的概念使数学内容之间的相互关系逐渐清晰，理解与应用数即为一种心理活动．数目聊念的成立基于四则运算，接触数源于测量，测量为几何学的起源．代数的高级抽象需要学习者以识数、理解数与实际的关系为起点．相同或不同数之间不同方式的结合为数学发展提供可能，同时其又反作用于数本身．

3 算术学习心理及其实施

数概念及相互关系的认识为学习四则运算扫清了障碍．四则运算是算术学习心理的重要研究内容．四则运算顺序均与人类的经验和习惯、社会发展有关，这就需要以此为基础来研究四则运算的一般心理过程．四则运算本身就是一种结合（民国时期算学名词，数之间发生关系可称为结合，例如加减乘除都属于结合），民国时期的研究者们对此难易程度进行了研究．所有运算都离不开练习，练习的形式和时间均对算术的学习产生积极的影响．

3.1 四则运算的心理过程

在研究算术学习心理的过程时，民国时期的研究者们多以四则运算的发生及发展过程作为研究对象．言简意赅地阐释了加减乘除的概念，即集合诸物为一处，可得到加的概念；在诸物中抽去几个，则得到减的概念；将几组数目相等的事物放于一处，则得到乘的概念；在诸组中取出几组数目相等的事物，则得到除的概念[7]．四则运算是算术的基本技能，那么为什么四则运算顺序依次为加减乘除？当时研究者们认为加减乘除的四则运算中，乘法是加法的特殊情况，除法是减法的特殊情况．加法先于减法，与学习者经验习惯有关．因为学习者计数一般自小到大，逆向计数比较困难．乘法先于除法是因为除法会遇到有因数的数目，可除尽无余数，才较为妥当，而乘法则不需要顾及此种情况．除了乘除法关系密切外，乘除法的意义可以帮助学习者进一步理解比例的原理．例如，“二”如果作为“六”的单位，则可分为3组，“二”是“六”的三分之一．至于与除法相关的分数，分数原与比例是一样的事情，可以说分数是比例的特殊情况，不过前者为后者的符号．百分比也不过是将分数的原理用于特别情形中，即用特别的方法代替分数．如果学习者知道十进位分组法（decimal form of grouping），慢慢就会懂得百分比是一种分数的变形．百分数可理解为以百代数量的全体，然后计算其部分的比例．但不论学习者学习分数还是百分数，起初都需要用实物进行说明学习．

此外，同一种计算方法，因为组合数目的方式不同，难易则不同．如7+4=11，同9+2=11，答案虽然都为11，但对于学习者来讲，困难程度却不同．民国时期加法结合难易的实验较多．如汤鸿翥的《加法基本结合难易之实验分析》[8]中斯密史（Smith）的加法结合难度比较实验（如图1）．邢绮庄的《算学整数四则的心理探讨》[9]中克伯屈（Kirkpatrik）的实验，如图2．

以上实验均可得到不同加法结合的难易程度的结论，白琅（Browne）、海尔孟（Heilman）和雪尔第斯（Shultis）将结论具体化，提出了有关于加法结合难度规律的结论，可以归纳为以下内容：比较容易相加的数目，是两数中有一个最小的数目，如1或2时[7]．

关于减法，杜佐周在《数学的心理续》[10]中提到了霍威尔（Howell）的实验，实验表明用较小的补充数为减数时，得到的成绩比较好．因此教师在教学时应慎重斟酌，变通教材，以适应学习者的需要．再如，减法计算过程中的借位，一般有两种方法：加添法与分减法．加添法是若两位数相减，减数个位上的数字大于被减数个位上的数字时，需要在十位上借“1”，这“1”需要“乘10”加入个位上（如85–17，7大于5，需要借一位，成为15），才能继续相减[10]．在此基础上，白莱特（Ballard）用实验的方法对两种方法进行了比较，结果发现加添法比分减法好用．现在的学生学习的也是加添法．

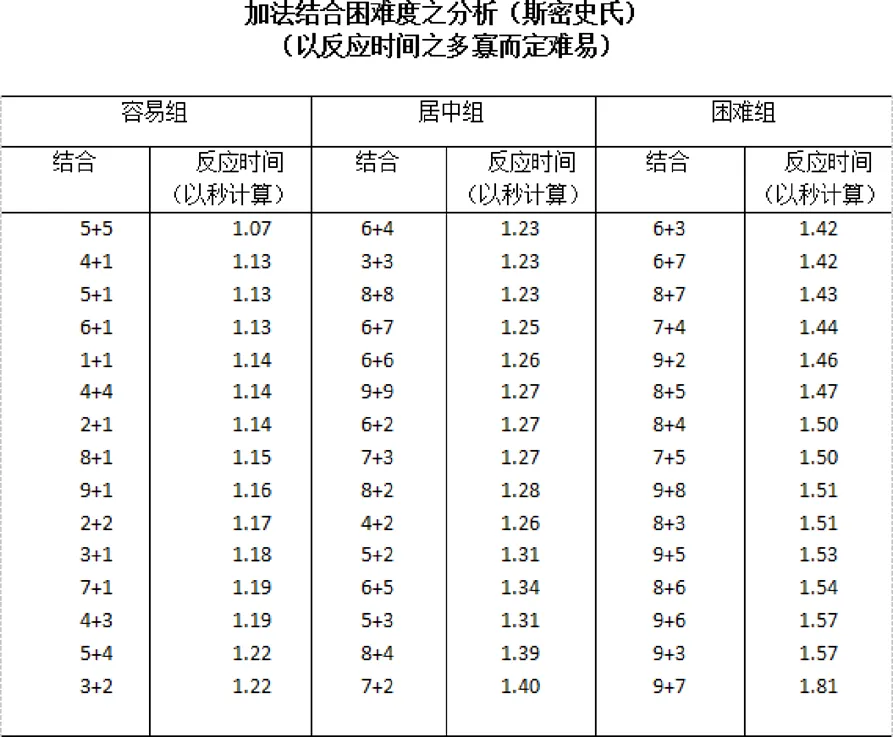
图1 加法结合难度比较实验

图2 克伯屈的实验

在除法方面，屈鲁雪尔（Drushel）通过实验比较了两种含有小数除法的方法．一是所得的商应有几位小数，则视被除数商的小数多于除数商的小数的数目为标准（适用于除得尽的小数）[10]．二是先用10或者其它适当数目乘以除数及被除数，化除数为整数，计算时按照整数除法计算即可．这与现在学生学习的化小数为整数是相同的．

3.2 算术的练习与巩固

美国联结主义创始人桑代克1922年出版了[11]一书，论述了学习算术过程和算术练习心理学的新观点．汤鸿翥等在研究桑代克等人的心理学学习理论时，也认同影响算术学习心理的因子分为先天的和后天的，后者包括：环境、聊念、情绪、练习等．桑代克提出的练习律、聊念律、满足律是研究算术心理的重要内容．满足律是通过结果或动作得到满足从而学习效率提高，聊念和满足的发生依赖于练习．

刺激与反应即为心理学研究的起点，刺激与反应相互作用可称为学习．刺激与反应相互作用一定次数，可以形成习惯，即为民国时期算术上的“绾结”（S-r bond），其与现在的“联结”一词相似．“绾结”既有利又有弊，有效的绾结需多加练习，无用的绾结要避免[12]．各种习惯的养成不外乎练习，想要练习纯熟依靠的条件比较多．如练习需要注意细节、练习者被动与主动地深入知识的程度及心向等都会对练习的结果造成影响．

汤鸿翥《聊念率与满足率》[13]、汤鸿翥《小学算学心理之研究（续）》[14]等著作均提到桑代克、美国教育家孟禄（Monroe）等人对算术与练习关系的研究，他们的实验结果表明算术欲求高效率，需要特别注重练习．练习时间的问题主要可归纳为以下两个内容：一是练习时间长短，二是练习时间的距离．把需要短时间的练习分配到较长的时期，这比需要长时间的练习分配在较短时间要好．如吴志尭《小学算术心理及教学法》[15]中甘贝（Kirby）的实验（如图3）及海恩（Heyne）和桑代克的实验均为练习时间与效率的实验（如图4）．关于算术推理练习，则用长时间训练比较适合．这与现在教育心理学所讨论的事实相符合，练习能得到较好的效率原因不在于练习本身，而是正当的配合或调节，即以正当之法获得练习真正之效果．

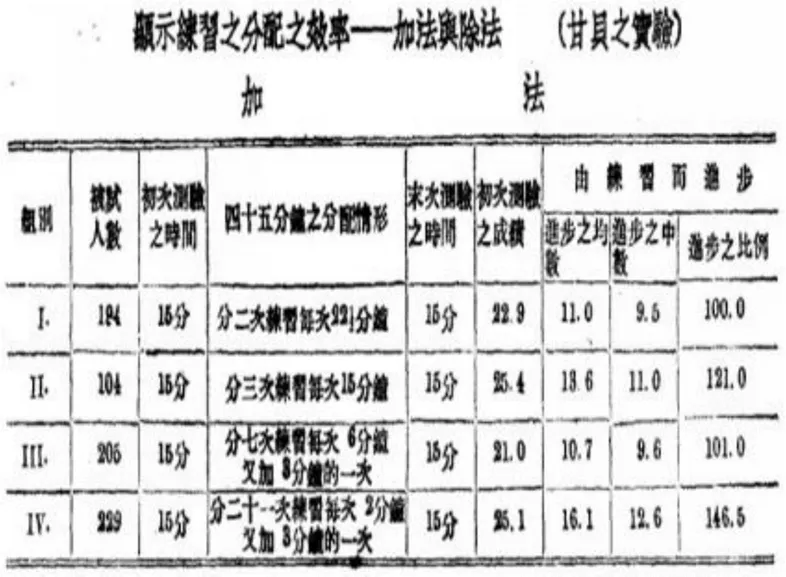
图3 甘贝的实验

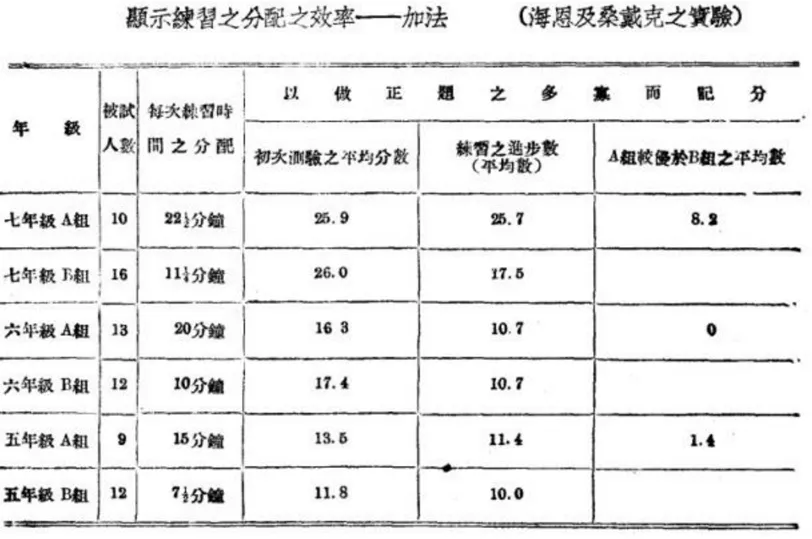
图4 海恩和桑代克的实验

杜佐周的《数学的心理续》[10]中提到的寇第斯（Courtis）的标准算术练习（Standard Practice Tests in Arithmetic）来源于美国纽约世界书局（World Book Co, Yonkers, N. Y），此练习测验完整且有灵活性，对现在的数学教育具有重要的参考价值，教育者和学习者可根据不同情况进行调整，分享如下．

（1）准备工作．

测验共含有四十八张片子，每张片子作为一次功课，各片子含有一种算术的例子，第十三、三十、三十一、四十四、四张片子为测量用．第四十五至第四十八张片子为后期学习用．功课自易至难进行．每进一课，就加一种算术上的困难．

除这种练习功课外，每个学生还需有透明纸做成的练习记录本．把每张片子放置于透明纸下，看见问题后，在透明纸上写下答案，便于这些片子以后继续使用，练习记录本上应有一页记录表和曲线等，学生自己记录每日的进步．

此外，教师也应准备一个记录本，本上记录关于应用练习功课及学生练习的详细说明，诊断学生困难的原因，并用适当的方法补救．

（2）关于练习测验的步骤．

先用第十三张片子（含有第一张至第十二张所有困难的问题）测验全体学生的程度，需在规定的时间内完成．

停止后学生交换练习记录本，教师报告对的答案，学生互相校对错误．

若学生第一次测验有错误，需练习第一课，即第一张片子．无误后往下练习，以此类推．

当学生练习完十二课时后，立刻用第十三张片子进行测验．

有时用第十三张片子测验两次比较妥当，凡没有错的学生，不必再练习第一张至第十二张片子的功课．可学习另外功课或者继续测验，找到需要练习的地方到有错的学生赶到为止．

当学生已有百分之九十熟悉前十三课功课时，则需用第三十张片子测量他们的程度，没有错误的同学，可免习自第十四课至第二十九课．若有错误，则从第十四课起，继续练习至二十九课为止，方法如前．

从此算术练习过程可以发现，它主要以讲练代替普通传授式教学，且对不同学习能力的学生具有分层学习的效果，定期的测验可以帮助学习者对一定阶段内所学的内容进行自我检测，激发学习动机，整个过程的循环性较好，学习者可根据自身的学习情况进行自主学习，这种方式也适用于代数和几何的学习．

4 代数学习心理及代数能力

算术和代数既有联系又有区别，代数比算术更具有抽象性，其需要的思维能力高于算术．代数适于思想的探讨，使学习者的思想超越实物，不受时间、空间限制．聊念能够帮助学习者更好地明白代数知识及能力的表现．代数能力由深信组织思想及训练决定．其结果和算术相同，养成习惯，继续研究困难的问题．代数能够锻炼及改进观察、表记符号分析、综合应用等能力，并适合改进各种思想，这就要求代数训练应用更有艺术能力的特性．

4.1 代数学习心理与算术学习心理的联系与区别

算术为数学之一分科，用数字以论述数之性质及关系者也；代数学为数学之一分科，而用记号以研究数之关系及性质也[16]．由于算术和代数存在联系和区别，所以它们的学习心理也是有联系和区别的．算术是经验的抽象，代数则是表记抽象[17]．所谓表记抽象是指代数经验者运用表记，其思维过程中回顾经验时，使它们相依而不离，如果学习者经验与心理活动远了，学习者就会出现迷茫，不知所向．由此可见，算术学习心理和代数学习心理并非是绝对不同的科学，后者是前者的进一步精神作用，但仍说明数目之间的关系，都强调学习应顺应学生心理发展特点．例如：

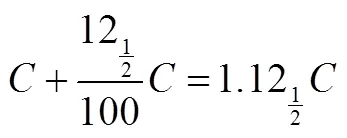
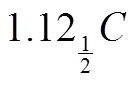
以此为例，当时研究者们发现较复杂或困难的问题，学习者用算术方法解决问题，几乎很难解决，但用代数符号解答，则无困难．当然，有些问题，算术与代数方法都可解答．那么其中代数所使用的符号就是研究者们接下来要讨论的问题了．在算术中每个符号，如3代表一定的数目，可用具体实物说明．代数中的符号代表的数目，并非固定的数，非实物，不常受数量的限定，即抽象的．如上例所用的符号代表一个数目，需等待问题解决才知道其数值．这种符号的用途是代替一个数目先使用，类似于未知数．方程式的应用就是一种抽象思维的过程．实际上，不仅如此，算术里的分数也包含数量抽象关系．总之，在有些问题中，代数方法比算术简便且计算容易，这是由代数本身的特征决定的．但随之代数需要的抽象精神作用也较高，这也是算术在历史的演变中进步的一个表现．

4.2 代数能力的特征

代数能力的实质是学习者对不同的代数问题作出不同反应的一种稳定特征，即有益心理联结与强化及无用联结的消除[18]．艾伟的《中学数学的心理》[1]概括出代数能力主要由4个方面构成，即公式能力、解释题与组织等式的能力、归纳能力和方程能力．

（1）公式能力．

公式用标记代替文字以陈述普通的法则，以解释一类问题中的任何问题．学习者除了了解公式的意义，还应具备自拟公式的能力．如=+，表示本利和=本银+本银×利率×时间．

（2）解释题与组织等式的能力．

解释题与组织等式的能力主要表现为理解题目，得到文字要素的数目价值，根据文字叙述给予较多的暗示组织等式．能否建立等式视学习者的能力而定，有能力的人，需要有灵活的表记运用，才能得到结果．学生理解数学知识的重要标志是学生能把语言表达、实际操作和具体运用这几方面结合起来[19]．例如：

父年三十八，母年三十二，子年十二，问几年之后，两亲之年适当子年三倍[1]？

可设年后两亲之年适当子年的三倍，父年为38+，母年为32+，子年为3(12+)，得：

38++32+=3(12+)

70+2=36+3

70–36= 3–2

=34（年数）．

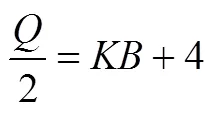
（3）归纳能力．

归纳能力对代数的学习颇为重要，代数问题如能多归纳，那就会将问题理解简单化[1]．例如：

3+3=(+)(2–+2)

86+279=[(22)3+(33)3]

=(22+33)[(22)2–(22)(33)+(33)2]

=(22+33)(44–623+96)．

学习者如果能理解前式，可知后面的一题出于一途，前者和为表记，后面的22与33为、的表记．学习者遇到问题，不能各树一帜，需要相互联系归纳[1]．

（4）演算推理能力．

学习者学习代数的普通方法是依照所学的原理或者规则演算，这应该属于习惯上的演算范围[20]．民国时期中等教育的学习者已具备有些概念、抽象的智力．虽然代数的法则都是由演算而来，但有些在此建立法则习惯的基础上，可驾驭新习惯．如2×=3，2×2=4，2×3=5，以此学习者可自行进行推理，可见理解规则的意义及何时应用需要多加注意．

虽然民国时期研究者们对代数能力的研究具有不完整性，多以代数内容本身的能力进行讨论，并未过多涉及教育心理学内容，但却表现出对学生能力培养的关注与重视，并结合实例进行了步骤分析及综合能力的归纳，其所倡导的方程能力、演算推理能力等仍是现在的课标所要求的．

4.3 代数能力与聊念之间的关系

王书林《中学学科心理》[5]提到许多学校对代数教学进行了改进，在过去算术学习的基础上，改变其结合以适合代数的应用．如果普通智力上缺失适当的指导及代数的结合，则在计算代数问题上容易出现问题．也就是说，代数的学习大部分是心智结合的组织和形式[18]．民国时期的研究者们已经开始注意代数结合的方式方法，注重聊念和组合的训练或心智习惯．

聊念能够帮助学习者预测在其它事情应用代数的能力和刺激学习者明白原理[13]．那么在民国时期关于代数的研究已表现出教育者应该培养学习者在学习过程中注意智力的积极构造，养成代数符号的结合，记忆代数的表记符号的意识．符号意识也是现在倡导的核心素养的主要内容之一，强调的符号意识主要强调意识的能动性．对于部分学生不能理解的问题，研究者们也进行了分析，学生对于解决问题时更多关注于数目、联结等，而忽视情境讨论、不注意名词的定义等习惯．

5 几何学习心理及几何能力

民国时期的研究者们认为学习几何需要对记忆、遗忘、想象、直观等心理过程有一定的了解，由此才能产生观念重组、归纳，从而促进数学思维发展．几何学与空间知觉关系之大，空间知觉帮助识图建模，为可能出现的答案提供可能．如某人立于岔路口，在感知选择的路，具有目的地的可能性，通过推理实证来确定其是否是目的地．

5.1 几何学习心理

几何学（Geometry）一词法文为Géométrie，产生于希腊文Γεωμετρία（原意是测量地球）．英国学校曾称几何学为欧几里得学，因其许多原理都是希腊数学家欧几里得（Euclid）所集成．它原是测量土地的工作而展开的学问．普通的测量虽不同于正式几何，但学习者如果有测量的经验，对后续学习测量、空间关系等原理会有一定帮助，即思想系统牢固，进步容易．几何的空间心理与代数的抽象心理是心理学中最完备且最令人满意的部分[20]．几何学习较算术及代数学习需要更高的精神作用，主要表现在几何要学习如何证明几何问题及这种关系的步骤理由[7]．当时的研究者们认为在学习算术和代数时，需将待解决的问题归在一类中，用一种普通的方法解决具体的问题．即已学习的方法应用于不同的动境（相当于现在的情境）中，研究发生的不同程序，因此几何需要的思维能力较大．

5.2 几何学习心理特征

几何学习离不开记忆．记忆的主要作用是通过刺激保留经验或者唤起所有的经验，它是心智中一种重要的能力，记忆的形式对于不同学习者而言难度不同．在学习后不能回顾就是遗忘，学习者对于几何中不明白的地方通过背诵，书本温习应用产生固定的保留，这是一种声音或者视觉的肌肉影像，非智能记忆，经过精细加工的记忆是复杂的，学习者能依所学有所用，这是思想的高级形式，这种记忆是抽象的，综合的．

想象是构造有效学习的一种重要方法．吴明慧、崔幼新的《中学数学心理》[20]谈到了想象，大意可归纳为：想象是感觉所得经验的要素，是可以进步的．学生在学习几何学时，若只观察事物或者图，而无适于心智想象的形式，是不能培养其特别的智力能力的．

几何要求学习者将空间分析组合成几何命题，然后分析它，用思维把握它[21]．所以指导学生应该选择其直觉思维的一方面，帮助学生形成抽象概念尤为重要，这与现在强调的数学直观是一样的．学生能够正确学习和应用空间几何知识的标准为对“图”的操作，既是学习空间的开始，也是学习几何的最后一部分[21]．也就是说，图属于直观呈现知识的一部分，要让学习者了解几何及空间，又在熟悉后不断地发现新的知识．

5.3 空间知觉在几何学习中的作用

学习几何学有“三法”，即实验法、实验而后证明法、逻辑证明法[1]．实验法，如对等边三角形3个角的度量，得出每个角均为60°；实验而后证明法，如实验之后知道长方形的对角线相等，证明其后，则以后遇到的任何长方形的对角线都相等；逻辑证明法，例如，若∠1与∠2一定不相等，则必然较小角或较大角为∠2，若证明∠2非较大角，则其必为较小角．由此可见，应用几何“三法”产生的心理活动是不同的．实验而后证明法和逻辑证明法具有一定交集，现在一般将后两种方法结合使用．

“三法”中的实验法需要对图形进行测量，也有不能测量的图形，如立体图形，对其观察需要空间知觉．空间知觉是指对物体距离、形状、大小、方位等空间特性的知觉[1]．空间知觉较为复杂，如艾伟的《中学数学的心理》[1]给出了3个图作为例子．在纸上画两条平行的直线（如图5），两直线之间相距一定距离，乍一看不能说两直线间的距离处处相等，每端加两条斜线，一条向内，一条向外，此时斜线平行吗？如图6，与是否在一条直线上？图7中，四边形是否内接于圆内？这些答案不敢轻易断言，原因大都是因为空间知觉复杂所致．

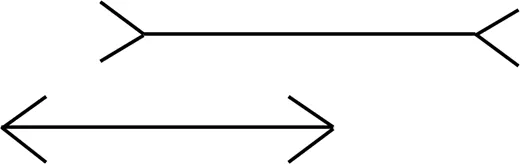
图5 两条平行线

空间知觉不仅是指视觉，其它的感知也同时存在，它是各种感觉相结合而成，相互产生关系后表现在意识中．由此可知研究者们已经认识到空间知觉与几何学关系之大，并且分为多种情况进行了分析．学习者在学习几何时需要先理解图形，如果头脑中没有相关的图形，学习则无从下手．学习者如果能够证明却不能识图，多是由于错误的空间知觉所致；能够画图但不能证明的学习者，多是因为不能找到图中的关系从而不能进行推论；知道图的构造却不能证明的学习者，多数是由于图和证明推理时所需要的心理相阻隔，不能相通所致[1]．了解空间知觉的发生和发展心理过程，可帮助学习者解决认知障碍和学习问题，而这也是现在数学教育一直在关注的重要问题之一．

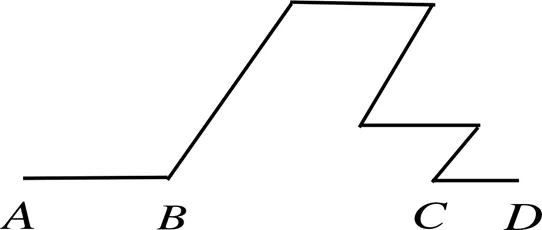
图6 线段共线

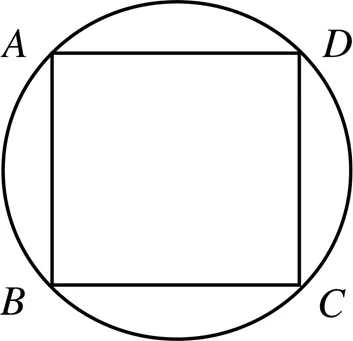
图7 四边形内接于圆

6 结语

民国时期为算学学习心理起步时期，是以心理学为基础、实验为依据，促进数学教育发展的重要阶段．当时的研究内容较为零散，未有研究将一堂课中从新知识的学习到巩固练习的学习心理过程完整进行阐述，且每个研究者对算学学习心理研究方向和内容均有不同．如汤鸿翥的论作主要阐述算术中四则运算的学习，未过多涉及代数、几何的学习心理，但讲述的内容较为具体，其中许多规律结果至今依然在沿用．在实验方面，偏重于不同结合的困难度实验及练习时间效率的实验．实验对象主要为中学生或者师范生，且进行了定量和定性的分析．如汤鸿翥的《加法基本结合难易之实验分析》[8]，邢绮庄的《算学整数四则的心理探讨》[9]等均涉及“结合”的难度实验，实验过程较为完整，实验结果对现在学习者、教育者、教材编写者都具有较高参考价值，但现在已被忽略或鲜为人知．望能引发更多学者的思考和对数学教育的发展献一份薄力．

[1] 艾伟．中学数学的心理[J]．心理，1923，2（3）：102–118．

[2] JUDD．中学学科心理[J]．刘蘅静，译．广东省教育会杂志，1925，2（6）：1–6．

[3] 汪子嵩．希腊哲学史（第一卷）[M]．北京：人民出版社，1997：65．

[4] 怀特海．文化科学—人和文明的研究[M]．曹锦清，译．杭州：浙江人民出版社，1988：9．

[5] 克罗．中学学科心理[J]．王书林，译．教育丛刊，1935，3（1）：159–191．

[6] 林崇德，杨治良，黄希庭．心理学大辞典[M]．上海：上海教育出版社，2013：143．

[7] 杜佐周．数学的心理[J]．教育杂志，1926，18（4）：29–59．

[8] 汤鸿翥．加法基本结合难易之实验分析[J]．中华教育界，1931，19（5）：55–68．

[9] 邢绮庄．算学整数四则的心理探讨[J]．教育杂志，1935，27（10）：1–8．

[10] 杜佐周．数学的心理（续）[J]．教育杂志，1926，18（6）：1–15．

[11]  EDWARD L T. The psychology of arithmetic [M]. New York: The Macmillan Company, 1922: 36.

[12] 汤鸿翥．小学算学与练习律[J]．中华教育界，1930，18（10）：19–28．

[13] 汤鸿翥．聊念率与满足率[J]．中华教育界，1930，18（7）：31–58．

[14] 汤鸿翥．小学算学心理之研究（续）[J]．教育杂志，1928，20（5）：6–18．

[15] 吴志尭．小学算术心理及教学法[M]．北京：商务印书馆，1949：43．

[16] 倪德基，鄜禄基．数学辞典[M]．上海：中华书局，1925：292．

[17] 艾伟．代数学之学习法[J]．学生学杂志，1923，10（6）：111–117．

[18] 陈琼，翁凯庆．试论数学学习中的理解学习[J]．数学教育学报，2003，12（1）：17–21．

[19] 吴明慧，崔幼新．中学数学心理[J]．教育研究，1935，25（10）：85–102．

[20] 艾伟．写在教育心理研究专辑之前[J]．教育杂志，1948，33（4）：1–8．

[21] 汤鸿翥．学科心理学导言[J]．中华教育界，1930，18（5）：1–10．

A Historical Review of Psychological Research on Mathematics Learning in the Period of the Republic of China

YANG Fan, DAI Qin

(Institute for the History of Science and Technology, Inner Mongolia Normal University, Inner Mongolia Hohhot 010022, China)

In the late Qing Dynasty and the early period of the Republic of China, western psychology works were gradually introduced into China. Following this, the results of western mathematical psychology research were introduced into China during the Republic of China. Chinese mathematics education researchers carried out research on mathematical learning psychology based on learning and absorption. This research consists of three categories: arithmetic learning psychology, algebraic learning psychology, and geometric learning psychology. Four operations are the main part of arithmetic learning. The form and time allocation of exercises affect the efficiency of arithmetic learning. Arithmetic is empirical abstraction, and algebra is descriptive abstraction. In some problems, the algebraic method is simpler than the arithmetic method, and students have shown high algebraic ability. During the period of the Republic of China, researchers believed that geometric learning required more complex psychological processes than algebra and arithmetic.

Republic of China; math learning psychology; arithmetic psychology; algebraic psychology; geometric psychology

G632.4

A

1004–9894（2021）05–0092–07

杨帆，代钦．基于学术史的民国时期数学学习心理研究[J]．数学教育学报，2021，30（5）：92-98．

2021–05–10

国家社科基金——蒙古族珠日海文献收集整理与研究（19VJX141）

杨帆（1990—），女，河北秦皇岛人，博士生，主要从事数学史与数学教育研究．代钦为本文通讯作者．

[责任编校：陈汉君、陈隽]