谈“多球相切问题”教学中数学核心素养的提升
2021-10-13黑龙江省大庆实验中学163316王英君
黑龙江省大庆实验中学(163316) 王英君
新一轮的数学课程改革提出六大核心素养: 数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析.如何将提升学生的核心素养落实到位,是当前中学教师亟需解决的问题.六大核心素养的提出,继承了上一轮课程改革的优秀成果,课堂教学将数学核心素养落实到位,学生才能理解数学.笔者在黑龙江省示范性高中“构建高效课堂,聚焦核心素养”数学学科教学研讨会上执教了一节高三理科复习课“多球相切问题”,在备课的过程中深入思考教学中如何落实数学核心素养,提升学生对问题的理解和解决能力.
1 分析高考真题,提炼关键信息
分析: 多球相切的题目侧重考查学生的空间想象能力,对作图能力要求较高.将球球相切转化为锥体问题,图形易上手,几何载体多变,以三角形中计算为主.
结论: 高考题目从几何作图和分析图形两个角度考查直观想象核心素养,同时考查逻辑推理和数学运算两个核心素养.
2 选择典型例题,提炼数学方法
例题把四个半径都是1 的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与前三个都相切,则第四个球的最高点与桌面的距离( )
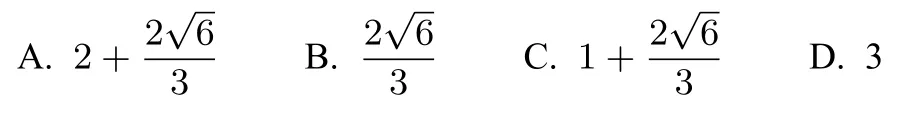
教学片段1:
师: 同学们,你们解答这道题的困惑在哪里?
生(齐答): 图形不好画.
师: 为什么画实际图?
小组合作交流: 用哪种几何图形代替球球相切? (教师展示直观图)
生1: 球心连线组成正四面体(替代图)
师: 如何求出? 请小组合作探讨一下.
生2: 先求四个球心连线是正四面体的高,而第四个球的最高点与桌面的距离即为高加上两个半径,从而求出所求.
解析: 四个球心连线是正三棱锥.棱长均为2,∴ED=∴第四个球的最高点与桌面的距离为OA加上两个半径即故选: A.
设计意图: 让学生有意识地去寻找替代图,认识球球外切等价球心连线线段长为两球半径和.体会勾股定理和射影定理在解决此类问题中的应用.使学生对高考题形成初步感知,掌握问题求解的一般思路,重点强化平面化方法.
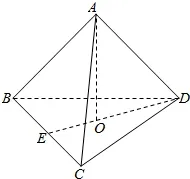
引申1.将3 个半径为1 的球和一个半径为√的球叠为两层放在桌面上,上层只放一个较小的球,四个球两两相切,那么上层小球的最高点到桌面的距离是( )
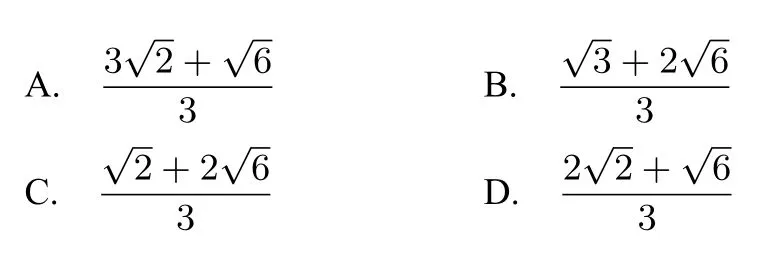
教学片段2:
师: 请同学们作出替代图,寻找突破口,并确定算法.
师: 你解答此题的困惑在哪里?
生: 不是正四面体了.
师: 可以解决吗?
生3: 设下层三个半径为1 的球的球心构成边长为2 的等边三角形,上面小球的球心和这个等边三角形构成侧棱长为的正三棱锥,上层小球的最高点到桌面的距离为小球半径、大球半径与正三棱锥的高相加之和.
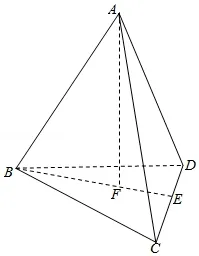
【解答】 解: 设下层三个半径为1 的球的球心分别为B,C,D,上层较小的球的球心为A,则ΔBCD是边长为2 的等边三角形,AB=AC=AD=过A作平面BCD的垂线AF,交平面BCD于点F,F是ΔABC的重心,则∴上层小球的最高点到桌面的距离是故选: A.
设计意图: 本题考查上层小球最高点到桌面距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.拓宽了解题视野.
3 开展头脑风暴,优化思维结构
引申2.已知四个半径为R的大球,上层一个,下层三个且两两相切叠放在一起,若在他们围成的空隙中,有一个小球与这四个大球都外切,另有一个更大的球与这四个球都内切,求小球的半径r1和大球的半径r2.
生【分析】: 我们易将这四个球的球心连接成一个正四面体,并根据四球外切,得到四面体的棱长为2R,正四面体的外接球半径为由于这四个球之间有一个小球和这四个球都外切,则小球的球心与四面体的球体重合,进而再由小球与其它四球外切,球心距(即正四面体外接球半径)等于大球半径与小球半径之和,得到答案.
小组合作解: 由已知中四个半径都是R的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与前三个都相切,连接四个球的球心,得到一个棱长为2R的正四面体,则该正四面体的外接球半径为若这四个球之间有一个小球和这四个球都外切,则这个小球的半径为另有一个更大的球与这四个球都内切,更大球的半径r2=
师【点评】本题考查的知识点是棱锥的结构特征,球的结构特征,其中根据已知条件求出四个半径为1 的球球心连接后所形成的正四面体的棱长及外接球半径的长是解答本题的关键.
引申3.现有两个半径为2 的小球和两个半径为3 的小球两两相切,若第五个小球和它们都相切,则这个小球的半径是( )


小组合作【解析】 如图所示,A,B是半径为2 的球的球心,C,D是半径为3 的球的球心,O是第五个球的球心.由题得CE=∴OE=因为AB⊥CE,AB⊥ED,∴AB⊥平面BEC,所以AB⊥EO.在直角ΔAEO中,(r+2)2=故选A.
师点评: 本题的难点在于画图和从线面关系里找到方程.所以首先要把图画得直观,再从几何图里找到线面关系利用解三角形的知识列出方程.
设计意图: 通过构造几何体得到问题的答案,本质是“建立数学模型”和“解答数学模型”的过程,提升了学生的几何直观素养和数学建模素养.凸显“模型化”方法的解题魅力.让学生进行研究性学习,提升认真钻研的科学精神.
思维导图如下:


