深度研究教材,让优术和明道同生长——以数学活动之探究四点共圆为例

广东省广州市第七十五中学(510500) 邹务姣

圆的内接四边形对角互补,这是在人教版九年级上册学习圆周角定理时得到的推论.在这一节新课教学中,时常会有学生追问,对角互补的四边形是否共圆呢? 教材正文及中考指导书上没有出现相关内容,所以,大多数教师在课堂教学中,对四点共圆的条件探究不深,而“四点共圆”是平面几何证题中一个十分有利的工具,在综合题和数学竞赛中经常出现.教材中这个内容以数学活动的形式出现,说明四点共圆这个知识,同学们很有必要去进行探究并掌握.与此同时,我们发现,有些题虽然表面与圆无关,但若能发现共圆的点,就能运用圆的丰富的性质为解题服务.

1 举一反三,运用意识唤醒

【教材】我们知道,过任意一个三角形的三个顶点能作一个圆.过任意四边形的四个顶点能做一个圆吗?

首先,我们思考一下,教材中为什么先提到过任意一个三角形的三个顶点能作一个圆这个结论呢? 这是因为过任意一个三角形的三个顶点能作一个圆,这是唤醒材料,它起到了“四两拨千斤”的作用,而且将要学习的新知与提到的这个旧知两个内容具有相似性,这样有助于“同化”新知识,这样,既能激发学生进行有意义学习的倾向,又能实现认知活动的螺旋上升.

在教学中,我们可以这样复习设问:

[师]: 怎样的三点可以确定一个圆?

[生]: 不在同一直线上的三点.

[师]: 过三角形的三个顶点能作一个圆吗? 如何确定圆心和半径呢?

[生]: 能.圆心是三边的垂直平分线的交点,半径是这个交点到三个顶点的距离.

教师展示作图过程.

【教材】分别测量下面各四边形的内角,如果过某个四边形的四个顶点能作一个圆,那么其相对的两个内角之间是什么关系? 证明你的发现.

接着继续这样提问:

[师]: 以前学习四边形的相关知识的时候,我们经常将四边形转化为两个三角形来解决,结合刚才的复习,观察以下三个图形,请同学们思考,过四边形的四个顶点能做一个圆吗?

过四点怎么作圆呢? 苏霍姆林斯基说:“在人的心灵深处,都有一种根深蒂固的需要,就是希望感到自己是一个发现者、研究者、探索者.”这就要求我们教师不仅要激发学生心灵深处的那种强烈的探究欲望,而且要让学生在探究互动中获得成功的情感体验,以促使学生保持足够的探究热情,进而产生强大的内在动力.这个问题的提出,意识唤醒它基于问题的探究,给学生探究问题、解决问题提供了广阔的思维空间,必将引发学生探究的欲望.

给学生充分的测量及思考时间,让学生通过学过的知识举一反三.

展示学生作图.

[师]: 通过作图,同学们发现了哪些图能作圆? 你是怎么作圆的?

[生]: 图一能作一个圆,连接BD,因为ΔABD和ΔCBD都是直角三角形,他们的外心都在斜边BD的中点处,以BD的中点为圆心,BD的一半为半径,这个圆经过四边形的四个顶点.

[生]: 图三也能作一个圆,通过作ΔABC和ΔDBC的外接圆,发现圆心是同一个点,半径是这个点都四个顶点的距离.

[生]: 图二过平行四边形的四个顶点不能作一个圆,作ΔABC和ΔDBC的外接圆,发现这两个三角形的外心都在各个三角形的内部,每个三角形都确定一个圆,这两个圆不重叠,所以过平行四边形的四个顶点无法确定一个圆.

[师]: 过四边形的四个顶点,有时能作一个圆,观察能作一个圆的图一和图三这两个四边形,观察它们的边角,你能发现它们有什么共同特征吗?

[生]: 它们对角互补.

[师]: 能举一反三的思考问题,很棒! 能归纳我们刚才过四点作圆的方法吗?

[生]: 两个共斜边的直角三角形的圆心在斜边的中点处.

[师]: 很好! 能注意特殊情况.

[生]: 将四边形分成两个三角形,先作其中三角形的外接圆,观察这个圆是否经过第四个顶点.

2 归纳验证,揭示数学本质

教材中由测量、猜想得到结论的方法,解决问题的入口宽,不失为一种帮助学生探究问题的好方法,这便于学生理解,能迅速得到四点共圆的条件,彰显了教材编写的智慧.

【教材】证明你的发现.如果过某个四边形的四个顶点不能作一个圆,那么其相对的两个内角之间有上面的关系吗? 试结合图形说明其中的道理.(提示: 利用圆周角与其所对弧的大小关系,考虑∠B+∠D与180 度之间的关系)

测量数据是表征,通过测量发现数学结论才是本源.为此,测量后,教师要让学生直逼数学本质.

[师]: 我们猜想对角互补的四边形能确定一个圆,这个仅仅是猜想,如何证明呢?

根据命题内容,写出已知、求证并作出图形.

[师]: 课本上有证明共圆的方法吗?

[生]: 圆的定义,也就是证明四个点到某点(圆心)的距离相等.

[师]: 某点如何找到?

[生]: 过三个点A、B、C可以确定这个圆心O.

[师]: 很好,那么如何证明第四个点也在圆上呢?

[生]: ——

[师]: 条件中,只有对角互补这个条件,难以得到点D到O的距离等于半径OA,还可以通过其他知识转化么?

[生]: 没有.

大部分学生陷入沉默.

[师]: 真是伤脑筋,直接证明有困难,同学们想一想,如果直接证明有困难的时候,我们还有其他的解决方案吗?

启发学生反向思考.

[生]: 反证法.

[师]: 很好,用反证法.点D在圆上的反面是什么?

[生]: 点D在圆内或圆外.

[师]: 对.我们先假设点D在圆内,这样会产生与题目条件或定理矛盾的结论吗?

结合图形,引导学生完成该过程的证明.

证明: 过A,B,D作圆O,假设C不在圆O上,则C在圆外或圆内,(1) 假设C在圆外,设BC交圆O于F,连结DF,根据圆内接四边形的性质得∠A+∠DFB= 180°,∵∠A+∠C=180°,∴∠DFB=∠C.而∠DFB为ΔDFC的外角,故∠DFB >∠C,所以假设错误,

(2)假设C在圆内时类似可以得到假设错误.所以原命题成立.由此,即可得到,对于四边形ABCD,对角互补⇒四点共圆.

掌握反证法是初三的教学要求,这种简明实用、独特思维方法和证题方法对提高学生创造性地分析问题和解决问题的思想素质有重要意义,也对培养学生的逻辑思维能力和解题技巧有所帮助.这里揭示了数学本质教学,让学生在学习中理解数学概念,把握数学方法,感悟数学特有的思维方式,鉴赏数学之美,追求数学精神.

3 拓展延伸,引领学生数学思维

从教材中归纳出证明四点共圆的方法:

思路一: 先从四点(数目不限)中先选出点作一圆,然后证另一点也在这个圆上.

思路二: 四点到某定点(中垂线交点)的距离都相等,从而确定其共圆(圆的定义).特例: 运用有关定理得到共底边的两个直角三角形,则四个顶点共圆,且直角三角形的斜边为圆的直径.

中考题1(圆的定义,隐形圆) : 如图,在RtΔABC中,AC= 6,BC= 8,点F在边AC上,并且CF= 2,点E为边BC上的动点,将ΔCEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是多少?

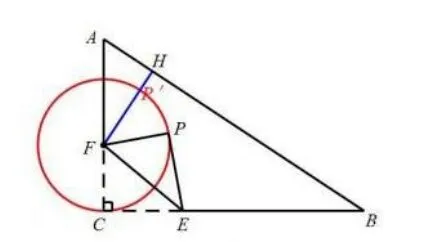
【分析】点E是BC边上的一个动点,导致点P也在运动,但是ΔPFE是由ΔCEF沿直线EF翻折得到的,所以FC=FP= 2 是不变的,由此可以得到点P的运动路径: 以点C为圆心,CF长为半径的圆.

解: 由题意得: 点P的运动轨迹如图所示,由垂线段最短可知,当FH⊥AB时,FH最短,若A、P、H三点共线时,PH最短.∵sinA=∴FH= 3.2,PH的最短值为: 3.2−2=1.2

中考题2: 如 图,ΔBAC和ΔDAE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连接BD,CE.

(1)求证:BD=CE;

(2)如图,延长BD交CE于F,连接AF,求∠AFB的度数.

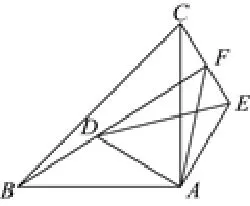
(1)求出 ∠BAD= ∠CAE,根据SAS推出ΔBAD∽= ΔCAE即可,过程略.

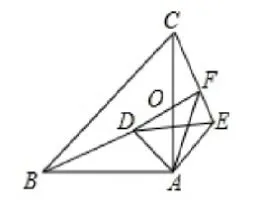
(2)分析: 设BF与AC交于点O,根据全等三角形的性质得出∠ACE= ∠ABD,求出∠CFO= ∠BAO=90°,推出D、A、E、F四点共圆,求出∠AFB= ∠DEA,即可求出答案.

解: 设BF与AC交于点O,∵ ΔBAD∽= ΔCAE,∴ ∠ACE= ∠ABD,∵ ∠COF= ∠AOB,∠OCF+∠CFO+ ∠COF= 180°,∠ABD+ ∠AOB+ ∠OAB=180°,∠BAO=90°,∴∠CFO=∠BAO=90°,∴∠OFE= 90°,∵∠DAE= 90°,∴∠DFE+∠DAE= 180°,∴D、A、E、F四点共圆,∴∠AFB= ∠DEA,∵在ΔADE中,∠DAE= 90°,AD=AE,∴∠DEA= 45°,∴∠AFB=45°.

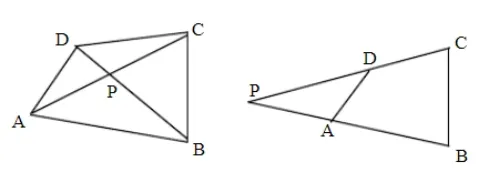
对于学有余力的同学,课外阅读资料还可以延伸:

(1)共底边的两个三角形顶角相等,且在底边的同侧,则四个顶点共圆.

(2)相交弦定理的逆定理: 对于四边形ABCD其对角线AC、BD交于P,PD·BP=PC·AP ⇔四点共圆.

(3)割线定理的逆定理: 对于四边形ABCD其边的延长线AB、CD交于P,PD·PC=PB·PA ⇔四点共圆.

4 写在最后

数学阅读能力是数学思维的基础和前提.著名的数学家斯托里亚尔说:“数学教学就是数学语言的教学”,数学具有一定的抽象性,文字语言和符号语言转换频繁,这就给数学学习增加了难度,如何降低难度呢? 通过深度研究教材,就会发现教材的编写简略和条理性和严谨性,通过深度研读,充分思考后,会自然达到学习新问题和解决新问题的目的,让优术和明道同生长.