题组变式 起承转合*——以“反比例函数与图形面积”一课的设计为例

广东省广州市真光中学(510370) 苏国东

1 前言

反比例函数是初中数学函数模块的重点组成部分,也是中考的热门考点之一,其与图形面积的综合问题更是常常出现于中档题和压轴题当中.

“反比例函数与图形面积”作为“反比例函数”章节的一节专题课,目标是让学生通过学习掌握运用k的几何意义以及坐标法解决反比例函数中的相关面积问题.笔者从本课题目的选取、变式的设计、题组的构建等方面进行了精心打磨,采用“起承转合”式的教学架构予以呈现.

2 教学设计

2.1 “起”——新知建构

创设合理的问题情境,引起学生的认知冲突,激发学生学习的兴趣,通过有层次性的问题,以旧带新,构建新知.

2.1.1 题组1 的设计

题1.点(2,−3)在反比例函数y=上,则k=____.

题2.点(m,n)在反比例函数y=上,则mn=____.

题3.如图1,过反比例函数y=上任意一点P作PA⊥x轴于点A,PB⊥y轴于点B,连接OP,求证:S矩形OAP B=|k|,SΔOAP=SΔOBP=

图1

题4.如图2,点P是反比例函数图象上的一点,PM⊥x轴于点M,连接OP,若SΔP OM=1,则k=____.

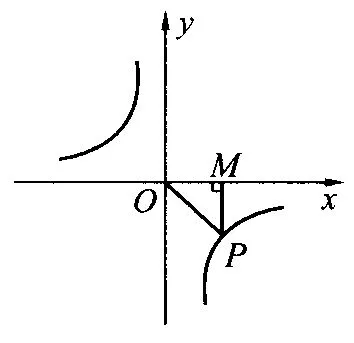
图2

2.1.2 教学分析

前三题的设计注重从特殊到一般,从代数到几何,为新知的建构创设了有“研究性”的问题情境;第4 题是对新知的正确辨析,从抽象到具体,突出新知的关键点,强调加绝对值的必要性.

其中第3 题在教学实践中,教师先利用几何画板演示图形变化,测量出矩形和三角形的面积为定值,再利用坐标法严谨证明这一结论.设点P(m,n),则PB=|m|,PA=|n|,mn=k,所以S矩形OAP B=PB·PA=|n||m|=|mn|=|k|,SΔOAP=SΔOBP=将此称为“k的几何意义”.坐标法的引入为后续解决非几何意义类的面积问题提供了代数的思路.

2.2 “承”——补充延伸

引导学生观察、分析、思考,承前启后,探寻知识的“生长点”,这个过程既是学生对新知的巩固运用,也是对新知的有效补充与延伸.

2.2.1 题组2 的设计

题1.如图3,正比例函数y=ax与反比例函数(k >0) 的图象交于A,C两点,作AB⊥x轴于点B,连接BC,则ΔABC的面积为____.

变式1.如图3,再作CD⊥x轴于点D,连接AD,则四边形ABCD的面积为____.

图3

变式2.如图4,正比例函数y=ax与反比例函数的图象交于A,C两点,AB//y轴,BC//x轴,则ΔABC的面积为____.

图4

2.2.2 教学分析

教师利用几何画板对不同颜色的图形进行显隐和变换,引导学生结合k的几何意义与图形的对称性,进一步求出一系列与|k|有关的图形面积.

第1 题及变式1 中,因为SΔABO=点A,C关于原点对称,所以SΔCBO=SΔABO=,SΔABC=|k|.

同理可得S.ABCD= 2SΔABC= 2|k|.利用坐标法再次验证: 设点A(m,n),则AB=|n|,BD=2BO=2|m|,所以S.ABCD=BD·AB=2|m||n|=2|k|.

变式2 中,当ΔABC为直角三角形时,由相似图形的性质可知其面积为ΔAOE的4 倍,即2|k|.由此还可推出矩形ABCD的面积是4|k|,梯形ABCF的面积为3|k|,点B,D都在反比例函数y=的图象上.

2.3 “转”——运用迁移

题组设计注重综合性与应用性,凸显解决方法的思想性与多样性,增强问题的“障碍性”,促进学生从学习数学知识向发展应用能力的有效迁移.

2.3.1 题组3 的设计

题1.如图5,将一矩形OABC放在直角坐标系中,O为坐标原点.点A在y轴正半轴上.点E是边AB上的一个动点(不与点A,B重合),过点E的反比例函数的图象与边BC交于点F,求证: 当点E运动到AB中点时,点F是BC的中点.

图5

图6

2.3.2 教学分析

第1 题的矩形并非k的几何意义中的矩形,但其实仍与|k|相关.教师引导学生从几何意义和坐标法两个方向进行分析.连接OB,因为SΔAOE=SΔF OC=点E是AB的中点,所以SΔAOB= 2SΔAOE=|k|,又因为SΔBOC=SΔAOB=|k|,所以SΔBOC= 2SΔF OC,点F为BC的中点.

第2 题是在题组2 的基础上进行的变式,添加了第二个反比例函数,同时AB不经过原点,本题无法利用对称性和k的几何意义解题,需要用坐标法解决.设点依题意有点),点B(−3m,),所以BP=m −(−3m) = 4m,PA=所以=8.

2.4 “合”——整合拓展

题组设计回归和体现知识的“整体”架构,关注多知识点的交汇及新旧知识的衔接整合,适度拓展创新,从而促进学生知识的融会贯通,提升数学学习能力和思维品质.

2.4.1 题组4 的设计

题1.如图7,一次函数y=x+4 与反比例函数y=的图象交于A,B两点,与x轴,y轴交于点M,N,连接OA,OB,求ΔAOB的面积.

图7

变式.如图8,一次函数y=−x+6 与反比例函数y=的图象交于A,B两点,与x轴交于点C,连接OA,OB,求ΔAOB的面积.

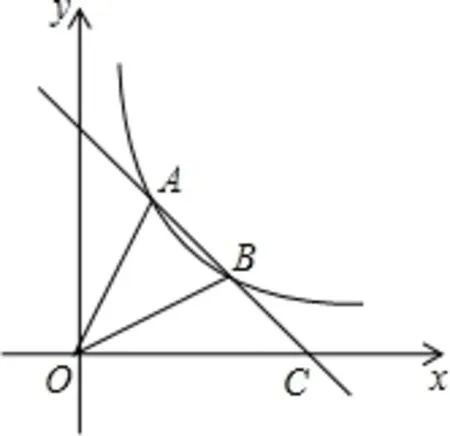
图8

2.4.2 教学分析

题组4 体现了反比例函数、一次函数与图形面积的知识交汇,从代数运算,到坐标转换,再到图形割补,让新旧知识得以串联与拓展.

第1 题教师引导学生观察图形,找出割补图形的不同方法,教师板书示范,思路如下: 联立两函数解析式,求出两交点A(2,6),B(−6,−2),易求得点M(−4,0),所以SΔAOB=SΔAOM+SΔBOM=

第2 题由学生自主探究不同解法,小组合作完成: 联立求出两交点A(2,4),B(4,2),求得点C(6,0),则SΔAOB=SΔAOC −SΔBOC== 6.教师追问学生,能否借助k的几何意义将所求面积进行转化,通过纵横拓展进一步发展学生思维.

如图9,过点A,B作AM,AN垂直x轴于点M,N,AM交OB于点E.因为SΔAOM=SΔBON=|k|,所以SΔAEO=S梯形EMNB,SΔAOB=SΔAEB+SΔAEO=SΔAEB+S梯形EMNB=S梯形AMNB,通过求解梯形AMNB的面积即可得出ΔAOB的面积.

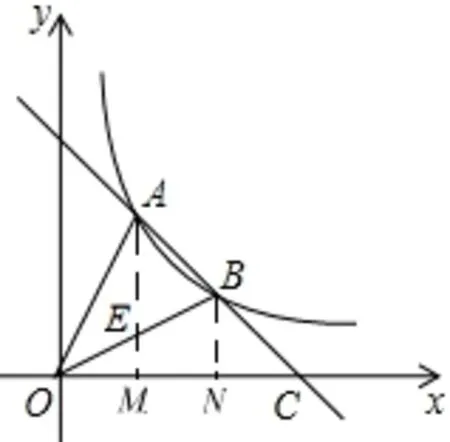
图9

3 设计反思

本课采用“起承转合”式的课堂教学架构,各个阶段通过问题引领,变式拓展进行串联设计,教学实践收到了较好的效果.具体的教学设计思路与流程可归结为图10 所示.

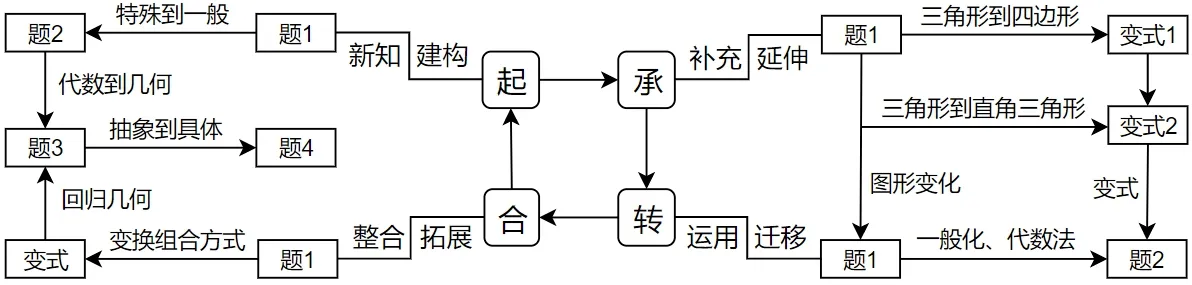
图10

3.1 起承转合,题组教学

“起承转合”式的教学设计分为四个阶段,以题组引导课堂教学.一是“起”的阶段,题组设计关注新旧知识的联系,创设适宜的问题情境,开展新知的建构;二是“承”的阶段,题组设计注重对新知进行有效补充和延伸,形成问题解决的多种策略;三是“转”的阶段,题组设计以解决核心问题为主线,培养学生的数学应用能力;四是“合”的阶段,题组设计体现知识的整合与衔接,发展学生的数学思维和关键素养.

3.2 问题引领,变式提升

问题是数学的心脏,教学设计注重问题引领.通过具有情景性的问题引入新知,具有研究性的问题检验新知,具有障碍性的问题辨析新知,具有生成性的问题延伸新知,具有应用性的问题实践新知;问题的设计注重联系、变式与拓展,如三角形与四边形、坐标与面积、代数与几何等数与形的变换,又如特殊到一般、抽象到具体、转化与化归等数学思想方法的体现.以题成组,以组构课,有效提升学生的关键能力和创新思维,促进数学课堂教学的优化.