动态问题的函数图象探究——函数图象判断的教学设计

广东省东莞中学松山湖学校(523000) 谈珊姗

1 内容和内容解释

1.1 内容

动态问题中的函数图象的判断,包含“点动型”、“面动型”和“线动型”三种类型.

1.2 内容解析

动态问题的函数图象一般以选择题形式考察,解决此类问题的方法一般有: (1)求解析式法;(2)判断趋势法;(3)定点排除法.本节课主要让学生学会如何分情况讨论,列出相应的函数解析式,然后根据函数解析式的特点作出相应的选择,进而总结提炼出破解此类问题更高时效的方法——判断趋势法以及定点排除法.列出函数解析式是联系题目本身(文字语言)以及函数图象(图形语言)的桥梁,综合运用了数形结合、分类讨论、函数与方程思想、模型思想,考查了学生分析问题、解决问题的能力,内容包括空间能力、应用意识、推理能力等,是近几年中考题的热点和难点.最后总结提炼出解决此类选择题的解题技巧,可以不需要求函数解析式,快速而准确地作出选择,提高解题速度.

基于以上分析,本节课的教学重点是: 对所给出的动态问题正确分类,建立函数解析式.

2 目标和目标解析

2.1 目标

(1)经历“点动型”以及“面动型”问题的探究过程,对问题正确分类;

(2)会列出函数解析式并选择相应的函数图象.

(3)通过对问题的分析,能够总结归纳出判断趋势法.

2.2 目标解析

达成(1)的标志是: 能阐述运动过程,根据图形形状进行分类;

达成(2)的标志是: 能列出函数解析式,熟练掌握函数的图象性质;

达成(3)的标志是: 本节课的主问题的分析过程要熟练,总结归纳方法快速解决牛刀小试中的个问题.

3 教学问题诊断分析

解决动态问题的关键是“动中求静”.对于“点动型”以及“面动型”问题,在运动中,对于图形变化进行正确分类是学生的难点,在运动中找到不变性是突破本难点的思路;同时,如何把图形变化转化为相应的函数图象,这对学生数形结合,函数与方程的思想提出极大的考验.

4 教学条件支持分析

利用几何画板和录播软件动态演示图象的变化过程,以几何直观呈现问题背景.

5 教学过程设计

5.1 教学流程图

5.2 目标导入,明确任务

本节课的学习目标:

(1)熟练掌握一次函数和二次函数的图象和性质,会根据图形运动建立函数模型;

(2)通过独立思考,合作探究,体会数形结合、分类讨论、函数与方程等数学思想.

师生活动: 教师PPT 展示本节课的学习目标,学生大声朗读.

设计意图: 通过朗读学习目标,学生能够明确本节课的学习任务.

5.3 课堂热身,感悟模型

师生活动: 学生自主完成问题1,小组抢答.

设计意图: 通过几道简单的与面积有关的求函数解析式的练习,让学生回顾一次函数和二次函数的模型,进一步复习巩固函数图象性质,让学生迅速进入课堂的学习.

问题1(自编)

1、如图,边长为4 的正方形空地上需要修葺两条宽为x的绿道,

(1)若剩余空地面积为y,请你写出y与x的函数关系式;并说出这个函数的图象及其图象性质.

(2)若绿道面积为y,请你写出y与x的函数关系式;并说出这个函数的图象及其图象性质.

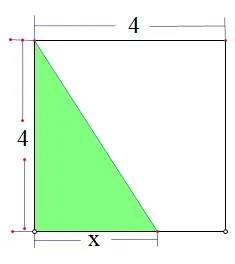
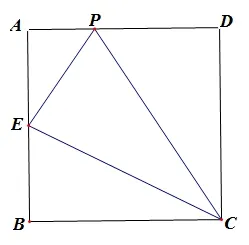
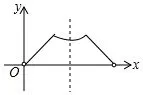
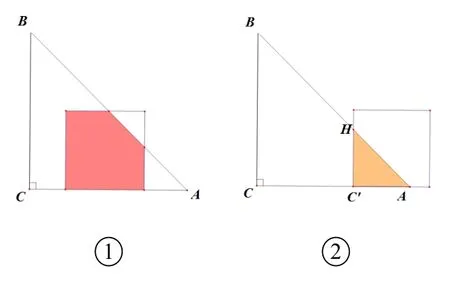
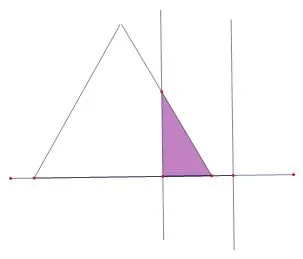
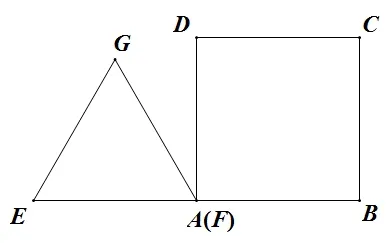
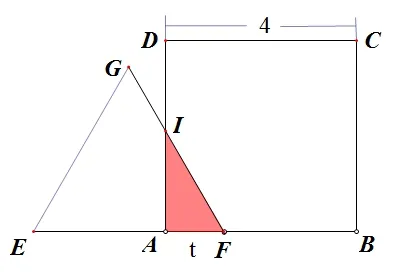
2、如图,边长为4 的正方形空地上需要修建一个与正方形等高的直角三角形的英语角,设直角三角形的底边长为x(0

(1)若直角三角形面积为y,请你写出y与x的函数关系式;并说出这个函数的图象及其图象性质.

(2)若剩余空地面积为y,请你写出y与x的函数关系式;并说出这个函数的图象及其图象性质.

解题思路: 对于规则图形,先用含自变量的式子表示出相关的边长,然后根据面积公式列出函数关系式;

对于不规则图形,可用割补法,用两个规则图形面积相加减的方法求出相应的函数关系式.

1、(1)剩余空地面积:y=(4−x)2,即y=x2−8x+16;图象是一条抛物线,开口向上,当x <4 时,y随x的增大而减小;

(2)绿道面积:y=16−(4−x)2,即y=−x2+8x;图象是一条抛物线,开口向下,当x<4 时,y随x的增大而增大.

2、(1) 直角三角形面积:y= 2x,图象是一条直线,当0

(2)剩余空地面积:y=−2x+16,图象是一条直线,当0

设计意图: 设计两道简单的函数与几何的题目作为抢答题,一方面有助于活跃课堂气氛,帮助学生尽快进入课堂学习,另一方面,让学生感悟用函数模型刻画几何图形面积的方法,并复习回顾一次函数与二次函数的图象性质,为问题2、问题3 的探究提供支持.

5.4 交流研讨,问题引路

问题2(2019•山东潍坊)如图,在矩形ABCD中,AB= 2,BC= 3,动点P沿折线BCD从点B开始运动到点D.

(1)(自编)动点P运动过程中,ΔADP的哪一边始终保持不变? 那么动点P沿折线BCD运动的过程中,ΔADP的面积应该分哪几种情况?

(2)(自编)设点P运动路程为x,ΔADP的面积为y,请写出每一种情况y与x之间的函数关系式;

(3)根据(2)中的函数关系式选出相应的函数图象( )

师生活动: (1)先让学生独立思考,并通过几何画板的动画演示带领学生了解整个运动过程,重叠部分的图形始终保持底边AD不变,只有高在变化,学生容易想到应当根据高的变化情况(即以折点作为分界)进行分类讨论;

(2)(3)让学生通过小组合作探究,把动态的三角形变化转化为几种静态的三角形求相应的面积,然后根据函数图象的性质选出相应的答案.

解答: ①当P在BC上时,如图.当0 ≤x≤3 时,y= 3,图象是一条平行于x轴的线段;

②当P在CD上时,如图,当3

综上,故选D.

设计意图: 从问题1 的静态图形求面积问题过渡到问题2 中的“点动型”求图形面积问题,先引导学生看到点动过程中所构成图形面积的不变量,即底边AD,则面积的变化取决于高的变化,因此我们得到的是一个一次函数的关系;根据高的变化情况进行分类,引导学生分类讨论,把动态的问题转化为几种静态的求图形面积的问题.体现数学的转化思想、数形结合思想、函数与方程的思想.

问 题3(2019• 四川省达州市) 如图,边长都为4 的正方形ABCD和正三角形EFG如图放置,AB与EF在一条直线上,点A与点F重合.现将ΔEFG沿AB方向以每秒1 个单位的速度匀速运动,当点F与B重合时停止.

(1)(自编)在这个运动过程中,正方形ABCD和ΔEFG重叠部分的形状有几种可能?

(2)(自编)在每一种情况中,请你写出相应的重叠部分的面积S与运动时间t的函数关系式;

(3)根据(2)中的函数关系式,请你选出重叠部分的面积S与运动时间t的大致的函数图象是( )

师生活动: (1)先让学生独立思考,并通过几何画板的动画演示带领学生了解整个运动过程,直观看到重叠部分的图形形状的变化,学生容易想到应根据图形形状进行分情况讨论;

(2)(3)让学生通过小组合作探究,把动态的图形转化为几种静态的图形求相应的面积,然后根据函数图象的性质选出相应的答案.

解答: 根据重叠部分图形的形状可分两种情况:

①重叠部分为三角形,如图.

②重叠部分为四边形,如图.

(2) ①当0 ≤t≤ 2 时,S=· t ·(t·tan 60°) =即S与t是二次函数关系,图象是抛物线,有最小值(0,0),开口向上.

◎过量的牛奶、巧克力、橘子在小儿体内可能产生变态反应，使膀胱膨胀，容量减少，并能促使膀胱平滑肌变得粗糙，产生痉挛。

② 当 2< t≤ 4 时,S=×42−(4−t)[(4−t)tan 60°] =(4−t)2,即S与t是二次函数关系,开口向下,

故选: C.

设计意图: 从问题2 的“点动型”问题过渡到问题3 的“面动型”问题,与问题(2)有所不同的是,问题3 在运动过程中,图形形状发生改变,进而求面积的方法发生改变,因此应该根据图形形状进行分类;同时区别于问题2 的,问题3 中构成的图形面积,其两个元素(底和高)都在发生改变,因此我们得到的是一个二次函数的关系.

问题2 与问题3 的设计都让学生感受到,无论是“点动型”还是“面动型”,关键是把动态的问题转化为几种静态的求图形面积的问题.体现数学的类比思想、转化思想、数形结合思想、函数与方程的思想.

5.5 师生交流,总结提升

问题4(自编): 再深入思考问题2 与问题3,对于动态问题中的图象选择问题,你有没有更加简便的方法能快速做出选择呢?

师生活动: 小组讨论,老师到小组中听取同学们的见解并适时做出指导,讨论结束后,请学生说出自己的想法.

生1: 对于“点动型”的问题是根据运动折线的数量进行分情况的,比如问题2 中沿BCD运动,则有BC和CD两条折线,因此应该分两种情况讨论;而对于“面动型”的问题,则根据图形形状的改变进行分情况.

生2: 我发现一个很神奇的规律,因为求图形面积一般都有两个元素,比如长方形面积由长和宽两个元素决定,梯形面积由(上底+下底)以及高两个元素决定,三角形面积由底和高两个元素决定,如果这两个元素中,只有一个元素在变化,那么它的面积就是一个一次函数,图象是一条直线,比如问题2;如果这两个元素中,两个元素都在发生变化,那么它的面积就是一个二次函数,其图象就是二次函数,如问题3.

生3: 接着刚刚那位同学的,我还总结出一个规律,如果一个元素在变,在运动过程中,越来越大的则这条直线是上升趋势的,反之,则是下降趋势;比如问题2 中,当点P从C运动到D的过程中,高在变小,因此直线是下降趋势,就可以不用求解析式直接作出选择;如果两个元素都在变,在运动过程中,两个元素变化趋势一样,则最终面积所对应的抛物线是开口向上的,反之,两个元素变化趋势相反,则最终面积所对应的抛物线是开口向下的.如问题3 中当0 ≤t≤2 时,重叠三角形的底和高都在变大,因此抛物线的开口向上;当2< t≤4 时,重叠图形是一个四边形,这个四边形可以看作是由一个定值减去一个底和高都在变小的三角形,因此所对应的抛物线应该开口向下;同时我们也可以把这个四边形看作是一个梯形加上一个面积固定的直角三角形,梯形的(上底+下底)变小,但是高却在变大,因此四边形的面积所对应的抛物线应该是开口向下的.

设计意图: 让学生深入探究图形面积与其元素变化之间的关系,总结出解决此类选择题的技巧,可以不用具体求出相应的函数关系式从而准确而快速地作出选择,即判断趋势法:

(1)先分情况,有几种情况就有几段图象;

(2)分析每种情况图形面积的构成元素是有几个在变化,如果只有一个,则图象是直线;如果是两个元素都在变化,则图象是二次函数;

(3)如果只有一个元素在变化,则图象的变化趋势与元素的变化趋势一致;如果两个元素都在变,当两个元素变化趋势一致时,抛物线开口向上,变化趋势相反时,抛物线开口向下.

5.6 牛刀小试,运用迁移

(1)(2019•铜仁)如图,平行四边形ABCD中,对角线AC、BD相交于点O,且AC=6,BD=8,P是对角线BD上任意一点,过点P作EF//AC,与平行四边形的两条边分别交于点E、F.设BP=x,EF=y,则能大致表示y与x之间关系的图象为( )

(2) (2019•浙江衢州)如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E →A →D →C移动至终点C,设P点经过的路径长为x,ΔCPE的面积为y,则下列图象能大致反映y与x函数关系的是( )

(3) (2019• 湖南衡阳) 如图,在直角三角形ABC中,∠C= 90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与ΔABC的重叠部分面积为S.则S关于t的函数图象大致为( )

(4)(2019 甘肃省天水市)已知点P为某个封闭图形边界上一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )

(5)(2018•莱芜)如图,边长为2的正ΔABC的边BC在直线l上,两条距离为1 的平行直线a和b垂直于直线l,a和b同时向右移动(a的起始位置在B点),速度均为每秒1 个单位,运动时间为t(秒),直到b到达C点停止,在a和b向右移动的过程中,记ΔABC夹在a和b之间的部分的面积为S,则S关于t的函数图象大致为( )

师生活动: 学生独立思考,然后小组讨论统一意见,老师给出适当的指导.

解: (1)解析式法: 当0 ≤x≤4 时,∵BO为ΔABC的中线,EF//AC,∴BP为ΔBEF的中线,ΔBEF∽ΔBAC,解得y=同理可得,当4

故选: A.

判断趋势法: 当0 ≤x≤4 时,y只与一个元素x有关,y随x增大而增大,因此图象是上升趋势的一条线段;当4

故选A.

(2)点P是沿E →A →D →C运动,则应该分三种情况讨论:

①当点P在AE上时,即当0 ≤x≤2 时,ΔCPE的高不变,底边在变大,因此,图象是一段上升的线段;

②当点P在AD上时,即当2< x <6 时,可以用铅锤法求ΔCPE的面积,水平距离不变,铅锤距离在变大,因此,图象是一段上升的线段;

③当点P在DC上时,即当6

因此选择C.

(3)首先根据重叠图形的形状分两种情况讨论:

情况①中的图形面积等于正方形面积减去直角三角形面积,直角三角形的底和高都在变大,因此情况①的函数图象是开口向下的抛物线;

情况②中重叠的图形是直角三角形,这个直角三角形的底和高都在变小,变化趋势相同,因此情况②的函数图象是开口向上的抛物线.

故选: C.

(4)首先分情况,y与x的函数图象分三个部分,而B 选项和C 选项中的封闭图形都有4 条线段,其图象要分四个部分,所以B、C 选项不正确; A 选项中的封闭图形为圆,开始y随x的增大而增大,然后y随x的减小而减小,所以A 选项不正确;D 选项为三角形,M点在三边上运动对应三段图象,且M点在P点的对边上运动时,PM的长可用勾股定理求解,如图所示:

PM长度取决于AM2,当M在P的对边运动时,AM2相当于两个AM相乘,它们的运动趋势是一致的,因此图象一定是一个开口向上的抛物线.

(5)此题如果用函数解析式法就会比较复杂,不妨采取趋势判断法:

①如图,当0 ≤t <1 时,面积S取决于两个元素: 直角三角形的底和高,这两个元素都在变大,因此图象是开口向上的抛物线;

②如图,当1 ≤t <2 时,面积S等于等边三角形的面积(定值) 减去两个直角三角形的面积.而这两个小直角三角形的底和高都在发生改变,并且变化趋势相同,因此图象是开口向下的抛物线;

③如图,当2 ≤t <3 时,面积S取决于两个元素: 直角三角形的底和高,这两个元素都在变小,因此图象是开口向上的抛物线.故选: B.

设计意图: 设计(1)是让学生感悟到解析式法和趋势判断法对于此题都比较容易;设计(2)(3)是为了让学生运用总结出来的解题技巧尝试快速解决“点动型”和“面动型”的函数图象选择题;设计(4)是让学生了解我们总结出来的解题技巧同时也适用于“线动型”的函数图形选择题.三种运动类型的共同点都是先分情况,然后分析所需元素之间的变化关系,根据变化趋势结合定点排除法,从而选择出相应的函数图象;设计(5)如果用函数解析式法相对比较复杂,但是如果采取趋势判断法,问题就大大地简化,让学生感悟根据具体的题目情况采用更简便的方法,提高学生分析问题、解决问题的能力.