不同维度 ZnO能带结构和电子态密度的研究

许钟华, 牙莉荀, 黄宝丹, 劳妃玲, 房慧, 陈春燕

(广西民族师范学院 数理与电子信息工程学院, 崇左 532200)

1 引 言

氧化锌(ZnO)是一种直接带隙的宽禁带半导体, 禁带宽度高达3.37 eV, 激子束缚能达60 meV, 具有优良的光电性质, 因在光电领域有着极大的应用潜力而备受关注[1]. 2004年, 单层石墨烯的发现使得人们认识了新的材料世界——二维材料世界. 二维材料展示出了许多新奇的特性, 如电子特性的增强、优良的机械强度和光学透明性质等并掀起了研究热潮[2-5]. 二维ZnO结合了ZnO和二维材料的性质特点, 能够提供或产生新的材料特性. 但ZnO在常温常压下的稳定状态为纤锌矿结构, 属于典型的三维材料, 不属于层状结构的二维材料, 所以获取二维ZnO较为困难, 目前关于二维ZnO材料性质的研究还较为缺乏.

2005年, Claeyssens和Freeman研究组[6,7]最早提出了ZnO材料形成单层结构的模型, 即ZnO薄膜材料沿着钛 (0001)方向或者(000-1)方向的厚度变得足够小时, ZnO便会由非层状的三维结构转变成类似石墨烯的二维结构, 即变成g-ZnO. 随后, Tusche实验组[8]在Ag(111)面上得到双层g-ZnO结构, 证实了Claeyssens和Freeman研究组理论预测结果的正确性, 这为二维ZnO性质的研究提供了基础. 但就目前而言, 二维ZnO的特性还有待进一步的研究和挖掘, 关于二维三维ZnO能带结构和电子态密度的异同以及维度对材料性质的影响还未有研究组进行深入的研究. 因此本文利用基于密度泛函理论(DFT)的第一性原理计算方法[9,10], 研究三维和二维ZnO的能带结构和电子态密度, 揭示维度的改变对ZnO能带结构和电子态密度的影响, 进一步补充二维ZnO的理论系统, 为二维ZnO基的器件研究提供了一定的理论参考.

2 计算参数与模型

采用基于第一性原理计算方法的VASP软件计算程序包来计算研究不同维度ZnO氧化锌材料的能带结构和电子态密度. 在计算过程中, 采用超软赝势(USPP)来描述离子与电子之间的交换作用, PW91参量作为广义梯度近似(GGA)中的交互关联泛函势. 平面波截断能为500 eV, 系统总能量的收敛判据为10-5eV/atom, 力收敛判据为0.01 eV/Å. 布里渊区K点网格取样采取Gamma方法, 对于三维ZnO, K点网格取值为11×11×11, 对于二维的ZnO, K点网格取值为11×11×1.

二维ZnO的构建方法为：在三维ZnO原胞的基础上, 沿着ZnO(001)面切出单层的ZnO结构, 将单层的ZnO结构扩展成为3×3×1的超胞结构, 共18原子, 其中9个O原子, 9个Zn原子, 最后添加10 Å的真空层以隔绝层与层之间范德瓦尔斯力的影响, 从而得到计算所用的二维ZnO模型.

3 结果和讨论

3.1 晶体结构优化

在计算不同维度ZnO的能带结构和电子态密度前, ZnO的初始结构模型采用了第一性原理的计算方法进行结构优化. 图1展示了优化后三维ZnO的结构示意图.从图1中可以看出，三维ZnO经过结构优化后仍然保持纤锌矿结构不变.

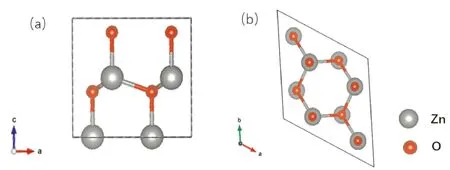
图1 (a)沿垂直c轴方向观察的ZnO结构示意图;(b)沿c轴方向观察的ZnO结构示意图.Fig. 1 (a)The structure diagram of ZnO observed along the direction perpendicular to c axis; (b)The structure diagram of ZnO observed along the c-axis direction.

图2展示了优化前后二维ZnO的结构示意图，从图2中可以看出: 优化前的二维ZnO中Zn原子与O原子不处于同一个平面内, 即成褶皱型；优化后的二维ZnO中的Zn原子与O原子共面, 即形成了类石墨烯的平面型二维结构. 但从c轴方向观察, 优化前后的二维ZnO都保持着六方的结构. 该实验结果证明了三维的ZnO沿着c轴减薄至单层原子时, 会变成类石墨烯的平面型结构, 即g-ZnO, 这一结果与前人的研究结论是相符合的[6,7].

图2 (a)沿c轴方向观察的优化前二维ZnO结构示意图; (b)沿垂直于c轴方向观察的优化前二维ZnO结构示意图; (c)沿c轴方向观察的优化后二维ZnO结构示意图; (d)沿垂直于c轴方向观察的优化后二维ZnO结构示意图.Fig. 2 (a)The structure diagram of un-optimized two-dimensional ZnO observed along the c-axis direction; (b)The structure diagram of un-optimized two-dimensional ZnO observed along the direction perpendicular to the c-axis; (c)The structure diagram of optimized two-dimensional ZnO observed along the c-axis direction; (d)The structure diagram of optimized two-dimensional ZnO observed along the direction perpendicular to the c-axis.

3.2 能带结构

为了方便对比分析不同维度ZnO的能带结构, 三维和二维ZnO的能带结构在计算时采用了相同的K点路径. 由于二维材料只有xy平面, 所以本文着重分析xy平面上的布里渊区点, 选择K点的路径为Г点到K点到M点再回到Г点. 通过归一化处理将费米能级移动到能量零点处. 图3中展示了三维和二维ZnO费米能级附近的能带结构图.

从图3中可以看出, 无论是三维ZnO还是二维ZnO, 计算得到的ZnO价带顶和导带底都位于布里渊区为Г点的位置, 这说明三维ZnO和二维ZnO都是直接带隙半导体.

从图3(a)中可以看出, 计算得到的三维ZnO的禁带宽度为0.90 eV, 这一结果与其他研究组计算的结果相近[13-15], 但是远小于ZnO的实际禁带宽度(3.37 eV). GGA的计算一般会导致ZnO带隙偏低, 但这并不影响对ZnO电子能带结构及电子态密度的定性分析[16,17].

从图3(b)中可以看出, 计算得到的二维ZnO的禁带宽度为1.85 eV, 是三维ZnO禁带宽度的两倍. 证明了维度的降低, 使得ZnO的禁带宽度变大.

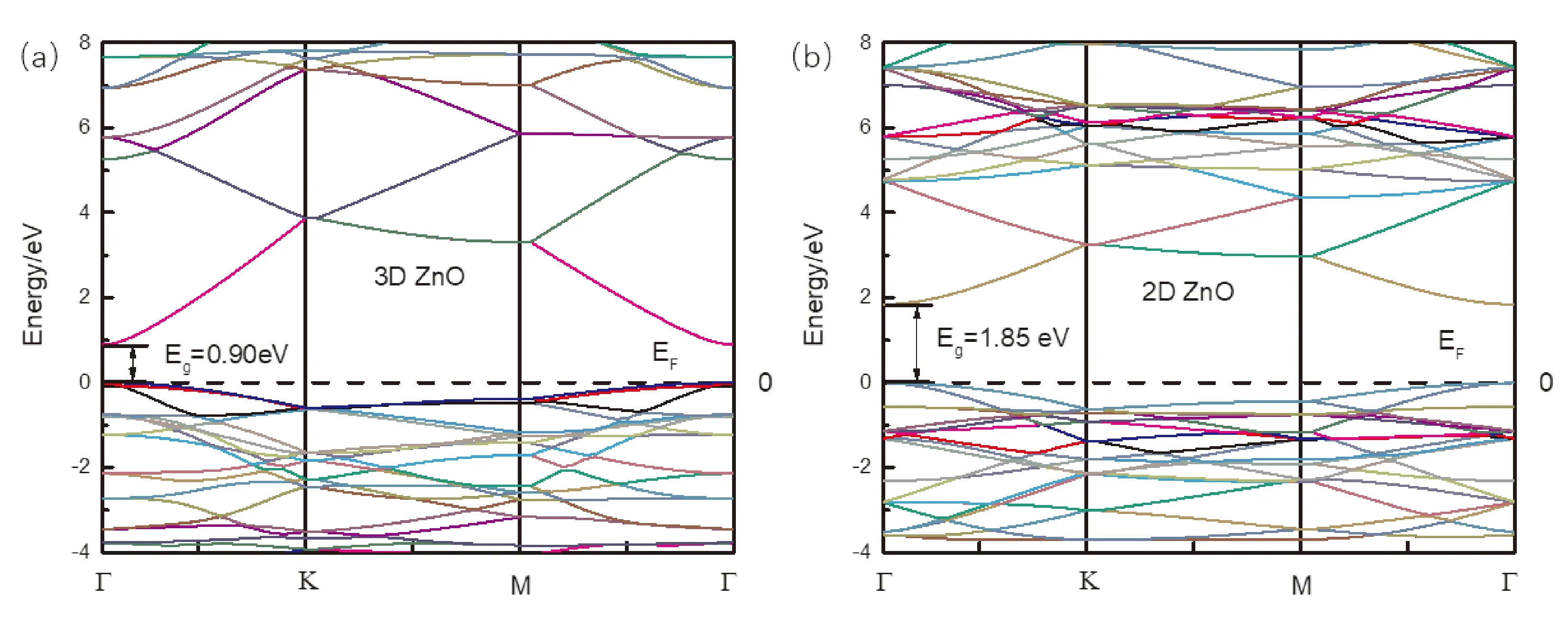
图3 费米能级附近(a)三维ZnO的能带结构; (b)二维ZnO的能带结构Fig. 3 Near Fermi level (a)band structure of three-dimensional ZnO; (b)band structure of two-dimensional ZnO

3.3 电子态密度

为了进一步研究三维和二维ZnO的电子态密度的异同以及轨道电子对态密度的贡献情况, 本文对三维和二维ZnO都进行了总态密度以及分波态密度的理论计算研究. 图4展示了三维和二维ZnO在费米能级附近的总态密度图.

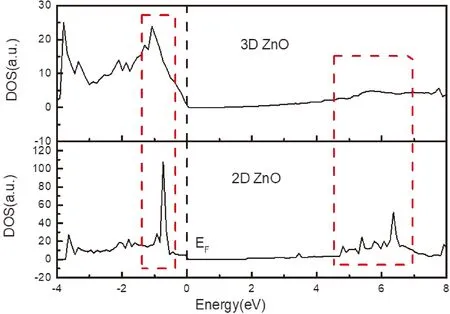
图4 三维ZnO(下)和二维ZnO(上)在费米能级附近总态密度图Fig. 4 Total densities of states of three-dimensional ZnO (lower) and two-dimensional ZnO (upper) near Fermi level

从图4中可以看出, 在价带顶(-4 eV～ 0 eV), 相比于三维ZnO, 二维ZnO在-0.73 eV的能量处出现了一个很尖锐的峰. 在导带范围(4.5 eV～7 eV), 三维ZnO的总态密度为一个平缓的小鼓包, 而二维ZnO的总态密度则出现很多小尖峰. 这些尖峰的出现说明二维ZnO的电子局域化程度比三维ZnO的更高. 这也是与实际情况相符合的, 在三维ZnO中, 电子可以在三个维度上运动, 而在二维ZnO中, 电子被局域在二维平面内运动, 因此在二维ZnO中的电子局域化程度更高.

为了进一步分析ZnO中的轨道电子对态密度的贡献, 本文分别计算了三维和二维ZnO的O 2s, O 2p, Zn 3d, Zn 4p, Zn 4s的分波态密度并在图5中展示计算结果.

图5(a)中展示了三维ZnO的总态密度和Zn 4s, Zn 4p, Zn 3d, O 2s和O 2p的分波态密度. 从中可以看出, 能量为-18 eV至-17 eV范围内的电子主要来源于O 2s轨道电子, 并有部分Zn 4p和少部分Zn 4s轨道电子的贡献, 此部分能量的与费米能级相距远, 与其他价带的作用弱, 对ZnO的性质影响不大. 三维ZnO价带低能端(-6～-2.5 eV)的电子主要来自于O 2p和Zn 4s的轨道电子, 并有少部分Zn 4p和Zn 3d轨道电子的贡献. 三维ZnO价带的高能端(-2.5 eV～0 eV)的电子主要来自于O 2p轨道电子的贡献, 并有少部分Zn 4p和Zn 3d轨道电子的贡献. 导带区域的电子主要来自于Zn 4s轨道电子, 同时有少部分的O 2p、Zn 4p和Zn 3d轨道电子的贡献.

图5(b)中展示了二维ZnO的总态密度和Zn 4s, Zn 4p, Zn 3d, O 2s, O 2p的分波态密度. 从图中可以看出, 能量为-18 eV至-17 eV范围内的电子主要来源于O 2s轨道电子, 并有部分Zn 4p和少部分Zn 4s轨道电子的贡献, 相似的, 此部分能量的与费米能级相距远, 与其他价带的作用弱, 对ZnO的性质影响不大. 二维ZnO价带低能端(-6～-2.5 eV)的电子主要来源于O 2p和Zn 4s轨道电子的贡献, 并有少部分Zn 4p轨道电子的贡献. 二维ZnO价带的高能端(-2.5 eV～0 eV)电子主要来自于O 2p, Zn 4p以及Zn 3d轨道电子. 导带区域的电子主要来自于Zn 3d轨道电子, 同时有少部分的O 2p, Zn 4p和Zn 4s轨道电子的贡献.

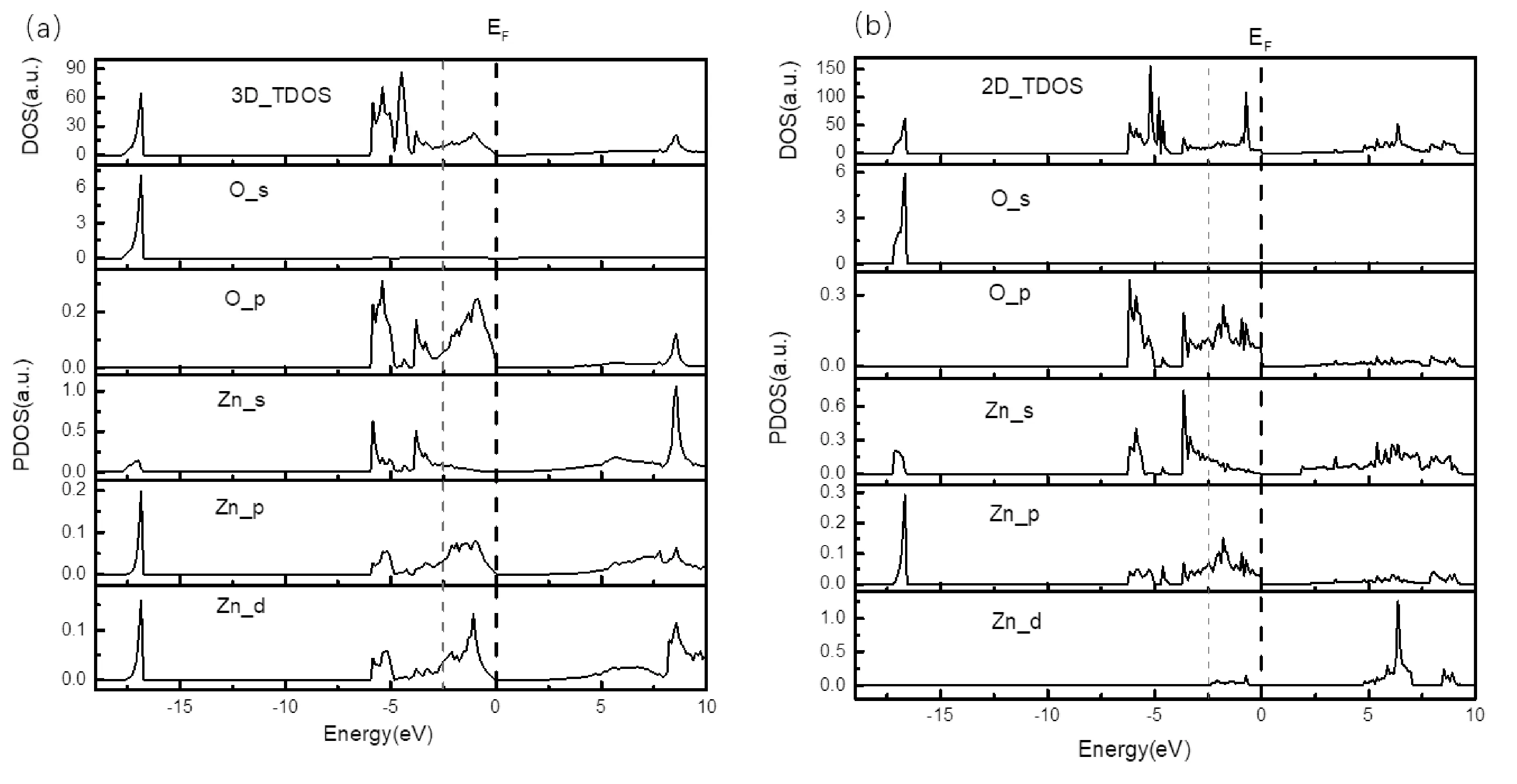
图5 (a)三维ZnO的总态密度和分波态密度; (b)二维ZnO的总态密度和分波态密度 Fig. 5 (a)Total densities of states and partial densities of states of three-dimensional ZnO; (b)Total densities of states and partial densities of states of two-dimensional ZnO

通过对比二维三维ZnO的分波态密度图可以得知: 相对于三维ZnO, 二维ZnO的O 2p, Zn 4s, Zn 4p, Zn 3d 轨道电子都有一定程度的局域化程度变高, 其中变化最大的为Zn 3d轨道的电子. 二维ZnO的Zn 3d轨道电子对价带低能端的态密度贡献减弱, 而对价带高能端和导带的态密度贡献增强. 由此可以知道, 当维度从三维变成二维时, ZnO的Zn 3d轨道电子从能量低的能级跃迁到了能量高的能级.

4 总 结

本文采用基于密度泛函理论的第一性原理计算方法, 对三维和二维ZnO进行了能带结构以及电子态密度的计算研究. 计算结果表明, 三维和二维ZnO都属于直接带隙半导体, 并且二维ZnO的禁带宽度要大于三维ZnO的禁带宽度. 从三维变到二维, ZnO的电子局域化程度变高, ZnO的Zn 3d轨道电子从能量低的能级跃迁到了能量高的能级. 本论文详细地分析了三维和二维ZnO能带结构以及电子态密度之间的异同, 揭示了维度的变化对ZnO能带结构和电子态密度的影响, 进一步补充了ZnO的理论并为二维ZnO基的器件研究提供了一定的理论参考.