高压下KMgF3晶体光学性质的第一性原理研究
2021-09-16孟川民
张 林, 张 莹, 付 勇, 何 林, 孟川民
(1.四川师范大学 物理与电子工程学院固体物理研究所, 成都610068; 2.中国工程物理研究院流体物理研究所 冲击波物理与炮轰物理重点实验室, 绵阳621900)
1 引 言
动态高压实验中, 材料的瞬态光谱和冲击温度测量常常需要用到透明的光学窗口[1,2]. 因此,冲击加载下窗口材料在可见光区能否保持透明的问题受到人们特别的关注[1,2], 因为它对实验结果的准确性有重大影响[3]. 虽然Al2O3和LiF晶体是目前常用的窗口材料[4,5], 但为了适应不同特性实验样品的加窗冲击测量, 人们还需要寻找新的透明窗口材料. 常态下, 氟化镁钾(KMgF3)由于具有巨大的能隙(12. 4 eV[6])和较宽的透明波段[7], 所以它有望成为一种新的候选窗口材料. 同时, 它在一个较宽的压力范围内可能保持结构的稳定也支持这个想法(KMgF3晶体在100 GPa的压力范围内保持Perovskite的结构[7,8]. 窗口材料的结构保持稳定,将有助于更好地解读加窗冲击实验数据). 然而, KMgF3能否真正成为冲击波实验的窗口材料, 关键还在于它在冲击压缩下是否能保持良好的透明性. 研究表明[2,9-12], 存在一些影响材料冲击透明性的因素(例如, 压力、空位缺陷和温度等因素). 所以, 探究这些因素对KMgF3晶体光吸收谱的影响具有重要的科学意义. 另外, KMgF3晶体在高压下的其它光学性质(例如,能量损失谱等)也是令人感兴趣且值得研究的问题, 因为它们对未来的实验探索可能有重要的参考作用.
目前, 对于上述问题的研究还未见报道. 所以, 本文将采用第一性原理方法, 在100 GPa的压力范围内计算了KMgF3理想晶体和含空位缺陷晶体的吸收谱和能量损失谱.
2 模型与计算方法

计算是在Material Studio 7.0下的CASTEP模块中完成的[14-16], 采用基于密度泛函理论(DFT)框架下的第一性原理来计算KMgF3晶体在高压下的光学性质[17]. 离子实与价电子之间的相互作用采用超软赝势来描述[18]. 用GGA的PBE方案来处理电子间的交换关联势. 几何优化采用了BFGS算法[19], 优化计算的精度由下面条件控制:最大位移偏差为0. 002 Å, 最大应力偏差为0. 1 GPa, 原子间的相互作用力的收敛精度为0. 05 eV /Å, 自洽收敛精度为2×10-5eV /atom. 为了证实计算的收敛, 平面波截断能取为310 eV. 对于KMgF3的理想晶体和缺陷晶体的计算, K点均设置为2×1×2, 空带数均为144.
为了说明计算数据的合理性, 我们做了如下一些分析:1)本文在零压下计算得到的KMgF3能隙值与文献[7]中计算得到的数据基本一致(见图1), 而且从其能隙随压力变化的规律来看,本文的计算结果与文献[7]给出的结果很相似(见图1), 这一切都表明本文的计算数据应该是可靠的. 2)KMgF3晶体在零压下计算得到的能隙值比其实测值[6]低约5.8 eV. 这种差异通常是由第一性原理计算理论的局限性造成, 可视为一种系统误差[20]. 所以, 本文计算的光学数据还需实施系统误差修正.
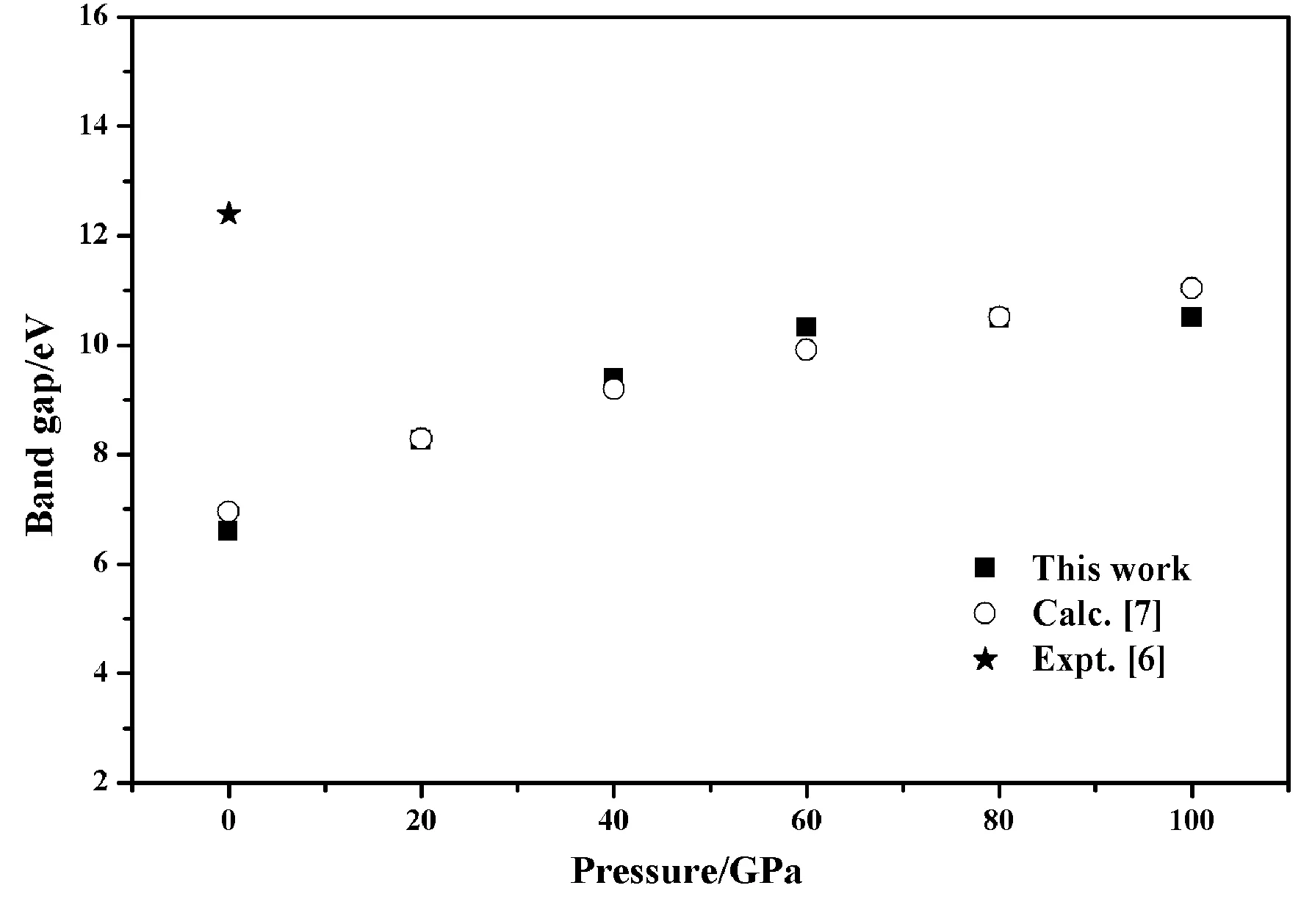
图1 KMgF3晶体在高压下的能隙Fig. 1 The band gaps of KMgF3 crystal at high pressure
3 计算结果与讨论
3.1 吸收谱

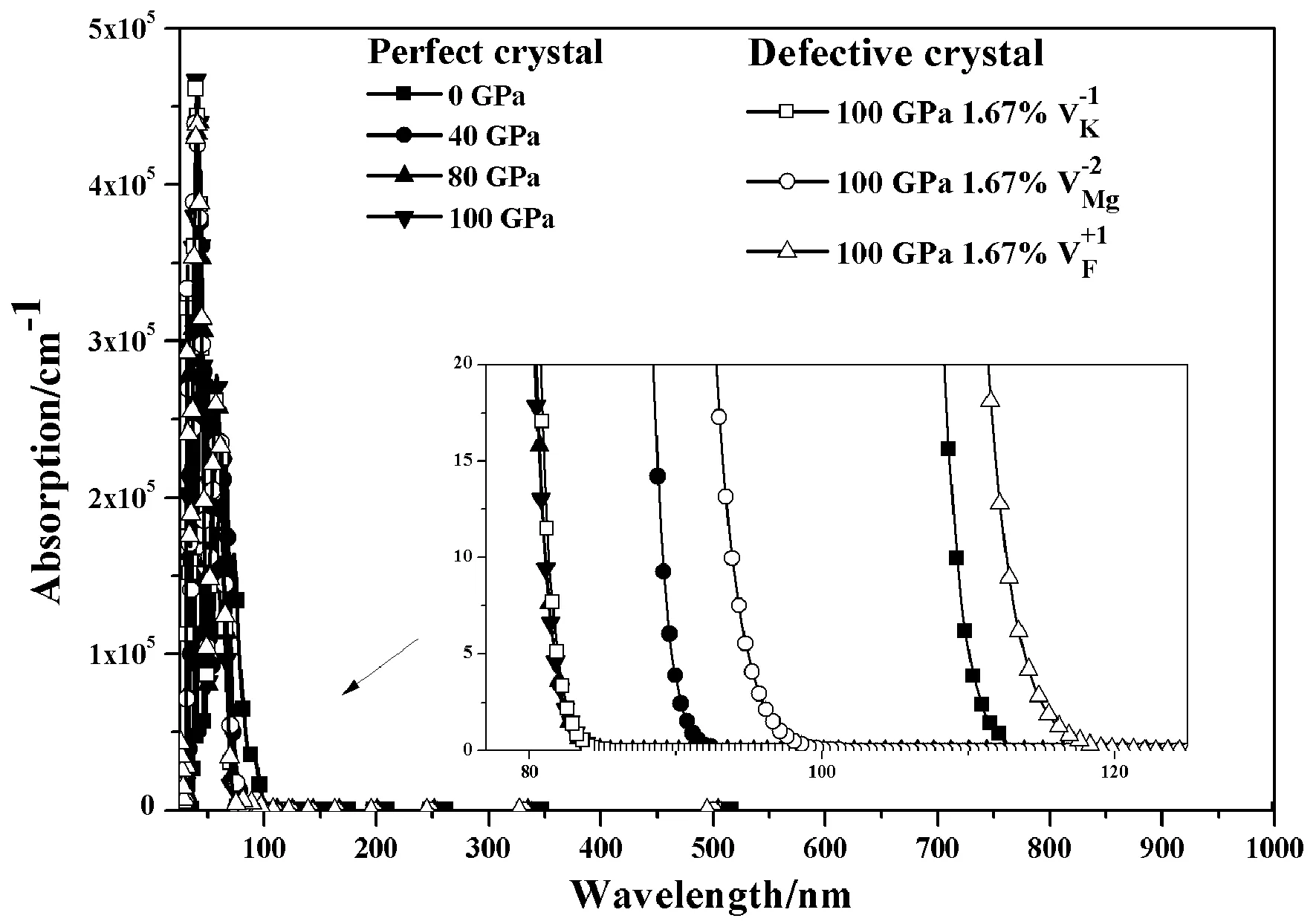
图2 KMgF3晶体在高压下的光吸收谱Fig. 2 Optical-absorption spectra of KMgF3 crystal at high pressure
3.2 能量损失谱


图3 KMgF3晶体在高压下的能量损失谱(a)理想晶体, (b)缺陷晶体Fig. 3 The loss-function spectra of KMgF3 crystals at high pressure: (a) Perfect crystal, (b) defective crystal
4 结 论

(1) KMgF3晶体吸收谱的吸收边会随着压力的增大出现蓝移的现象, 即在100 GPa范围内, 压力因素不会导致该晶体在可见光区出现光吸收的现象. 三种空位缺陷的存在会使得KMgF3晶体的吸收边红移, 其中氟空位缺陷引起的红移最显著. 尽管如此, 这些红移并未使得KMgF3晶体在可见光区有光吸收行为.
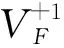
(3)KMgF3晶体有可能成为冲击波实验所需的窗口材料,同时本文的计算结果对未来的实验研究有一定的参考作用.
