激光驱动晶体发射低阶谐波强度随激光波长的变化规律

火勋琴, 管 仲, 周效信

(西北师范大学物理与电子工程学院, 兰州 730030)

1 引 言

在过去的三十多年里，强激光场与气体原子分子相互作用发射高次谐波的研究已取得突破性进展并被广泛应用于多个领域，如利用高次谐波来实现分子轨道的成像[1]、合成超短的阿秒脉冲[2]以及新的XUV光源[3]等，这些应用都是基于原子分子发射的高次谐波. 近年来，人们将研究领域扩展到晶体在激光场中发射的高次谐波，晶体具有密度大，周期性势的特点，与原子分子的结构有明显不同，因此，对晶体在强激光场中发射高次谐波的研究引起了人们的极大关注.2011年美国斯坦福大学的Ghimire等人将波长为3250 nm的激光聚焦到厚度为500 μm的ZnO晶体上，首次在实验上观测到强激光场驱动晶体产生的高次谐波，谐波谱表现出清晰的非微扰特性，截止频率达到25阶[4]. 随后便涌现出大量这方面的实验和理论研究，从而揭示出与强激光场中原子分子发射高次谐波的区别与关联. 已有的研究结果表明，强激光驱动下晶体发射高次谐波的过程与原子分子发射过程既有相似又有明显的不同. 相同的是都发射奇次谐波，也有平台区域和截止位置，不同的是晶体谐波的截止位置不是随激光的强度成正比，而是与激光的电场振幅成正比，经过细致的研究，Vampa等人[5]也提出了与原子分子发射谐波相对应的“三步模型”来解释晶体发射谐波的机理: 首先，在最高价带的电子隧穿到导带，从而形成电子-空穴对，然后这个电子-空穴对在激光的作用下在晶格中做Bloch震荡并获得能量，最后当电子-空穴相遇并复合，就发射出高次谐波，其相应的能量为瞬间晶格动量对应点的带隙能量[6-8]. 由此可见，晶体材料发射高次谐波主要来源于电子波包在带内发生的布洛赫震荡以及带间的电子-空穴对复合，与原子分子最大的不同之处是第二步和第三步，对于原子分子情况，由于母离子和电子质量的巨大区别，母离子几乎是不动的，电子在激光场驱动下运动，在长波长驱动下，电子返回母离子复合前，电子在空间的演化时间较长，引起了电子波包的扩散效应很强，在晶体情况下，电子-空穴对都在运动，并且，在坐标空间可以看出[9]，电子有可能与原来的空穴相遇而复合，也有可能与邻近的空穴复合，这样就导致了电子波包的扩散相对于原子分子的情况有所不同，Liu等人[10]对晶体谐波第一平台的发射效率随激光波长的下降就没有原子发射谐波随波长衰减那么严重，如处于基态的原子发射高次谐波时其发射效率与波长的关系为η(λ)∝λ-x,[x=4-6][11-14]，这些研究表明，晶体中电子波包的扩散相对于气体原子而言要小. 但是，晶体低阶谐波的发射机理与第一平台的发射机理有所不同，因此，有必要对晶体发射低阶谐波的强度与激光波长的变化情况进行研究，本文从一维晶体模型出发，通过求解含时薛定谔方程，研究了晶体发射低阶谐波的强度随激光波长的变化情况，由于低阶谐波的发射机理与平台区域的发射机理不同，因此，可以预见晶体发射低阶谐波强度随激光波长的依赖关系会有所不同.

2 理论方法

在速度规范下，考虑一维体系下的激光-晶体相互作用，且激光的极化方向沿着晶体的晶格方向，体系的哈密顿量为(无特殊说明，均采用原子单位)

(1)

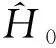
V0=0.37a.u.

(2)

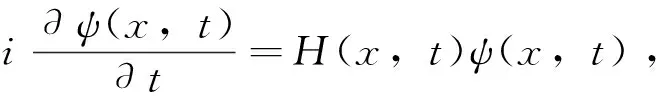
(3)

在动量空间，我们对(3)式进行求解，在求解的过程中，可以用无外场时的布洛赫态作为基函数，也可以用含时的休斯顿态作为基函数对体系的含时波函数进行展开.利用休斯顿态将体系的含时波函数进行展开时，可以把带内电流和带间电流对高次谐波的贡献分别进行处理，所以我们用休斯顿态作为基函数对(3)式进行求解.休斯顿态是含时哈密顿量的瞬态本征态，即[18]

(4)

其中n表示能带的指标，En(k(t))表示某时刻第n个能带的本征值，再将休斯顿态按照B-样条函数进行展开[19]，然后将展开式代入(2)式，并向某一本征态投影后得到一个关于展开系数的广义本征值的矩阵方程，最后通过对角化方法得到展开系数，从而求出休斯顿态，这样，体系的含时波函数可以表示为

(5)

通过Crank-Nicolson方法进行演化[20]，假定在演化的初始时刻，所有电子都处于最高价带上，而所有的导带都是空的.在每一个k0下，我们得到总的密度电流

(6)

总的电流可分为带内电流和带间电流两部分

jk0=jintra+jinter

(7)

带内电流的贡献只涉及相同能带上的休斯顿态，带间电流的贡献涉及不同能带上的休斯顿态,密度电流分别表示为：

(8)

(9)

给密度电流乘以一个Hanning窗函数，然后进行傅里叶变换，就可以得到高次谐波谱，窗函数的引入并不会影响激光峰值处晶体内产生的非线性电流.

3 结果与讨论

在对晶体发射谐波计算之前,首先对一维周期性势(2)式对角化得到晶体能带结构，由于第一个价带束缚得很深，因此我们在计算过程中将第二个价带作为演化的初态，且认为所有的电子在初始时刻都处于价带上.

在计算中，采用的激光场形式为

E(t)=E0cos(ωt)f(t)

(10)

E0为激光脉冲电场分量的振幅，ω为频率，f(t)为激光脉冲的包络，在计算中取f(t)为Gaussian包络，取脉冲的半高全宽为40 fs，总的激光持续时间为180 fs.

当激光强度为I=2.2×1011W/cm2，波长分别为3000 nm和6000 nm时，我们计算了晶体发射的低阶谐波谱，如图1所示. 由图可见，除第1阶谐波外，在6000 nm激光驱动下，所发射的第3阶、第5阶、第7阶和第9阶谐波都比3000 nm激光驱动下发射的强度要高. 由于第1阶谐波反映的是驱动激光的性质，因此在驱动激光强度相同的话，第1阶谐波强度相同，第9阶谐波的发射,由于能量已经涉及到导带到价带的跃迁，我们不对第9阶进行讨论，下面仅对第3、第5和第7阶谐波进行研究.

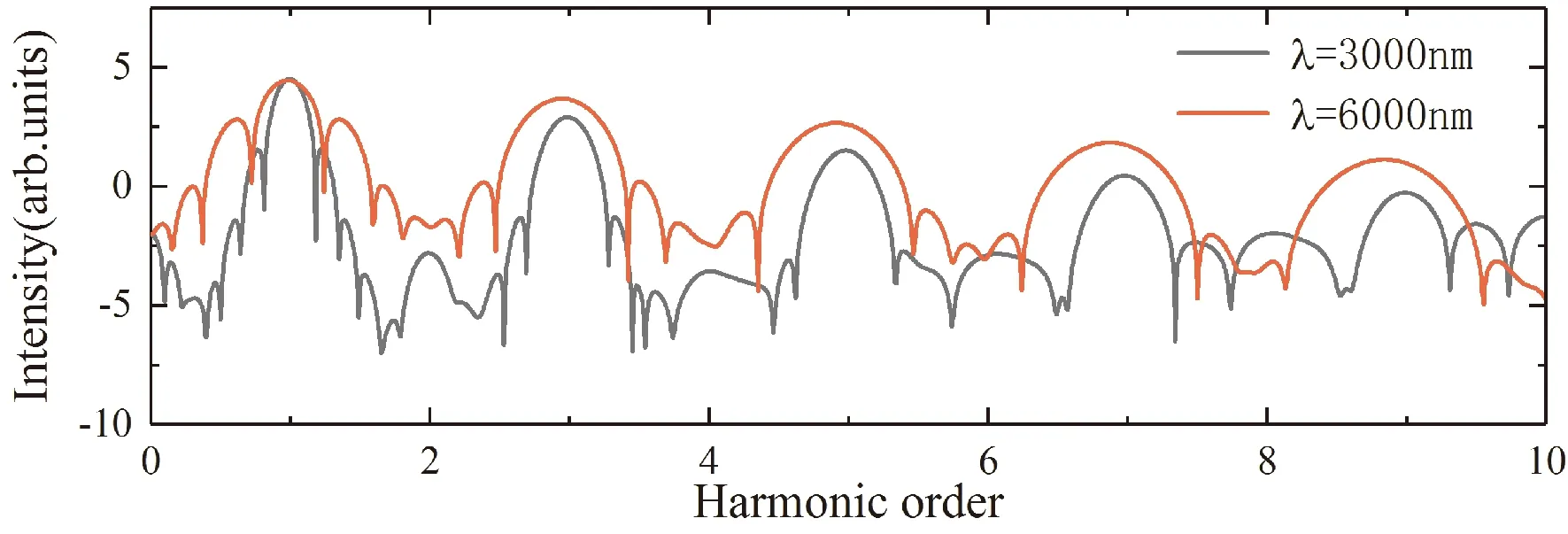
图1 激光波长分别为3000 nm和6000 nm时的低阶谐波谱Fig. 1 Low-order harmonic spectra at the wavelengths of 3000 nm and 6000 nm，recpectively

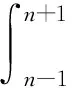
ΔY=βλk

(11)

为求得指数因子k，对(11)式求对数得到：

InΔY=Inβ+kInλ

(12)

通过最小二乘法，我们对InΔY和Inλ进行拟合，即可求出指数因子k.下面我们研究激光强度为I=2.2×1011W/cm2，我们计算了第3阶、第5阶和第7阶的谐波强度随波长的变化关系，在计算中激光波长从2000 nm变化到7500 nm，波长间隔为250 nm，计算结果如图1中的方块所示(图中采用的是双对数坐标).

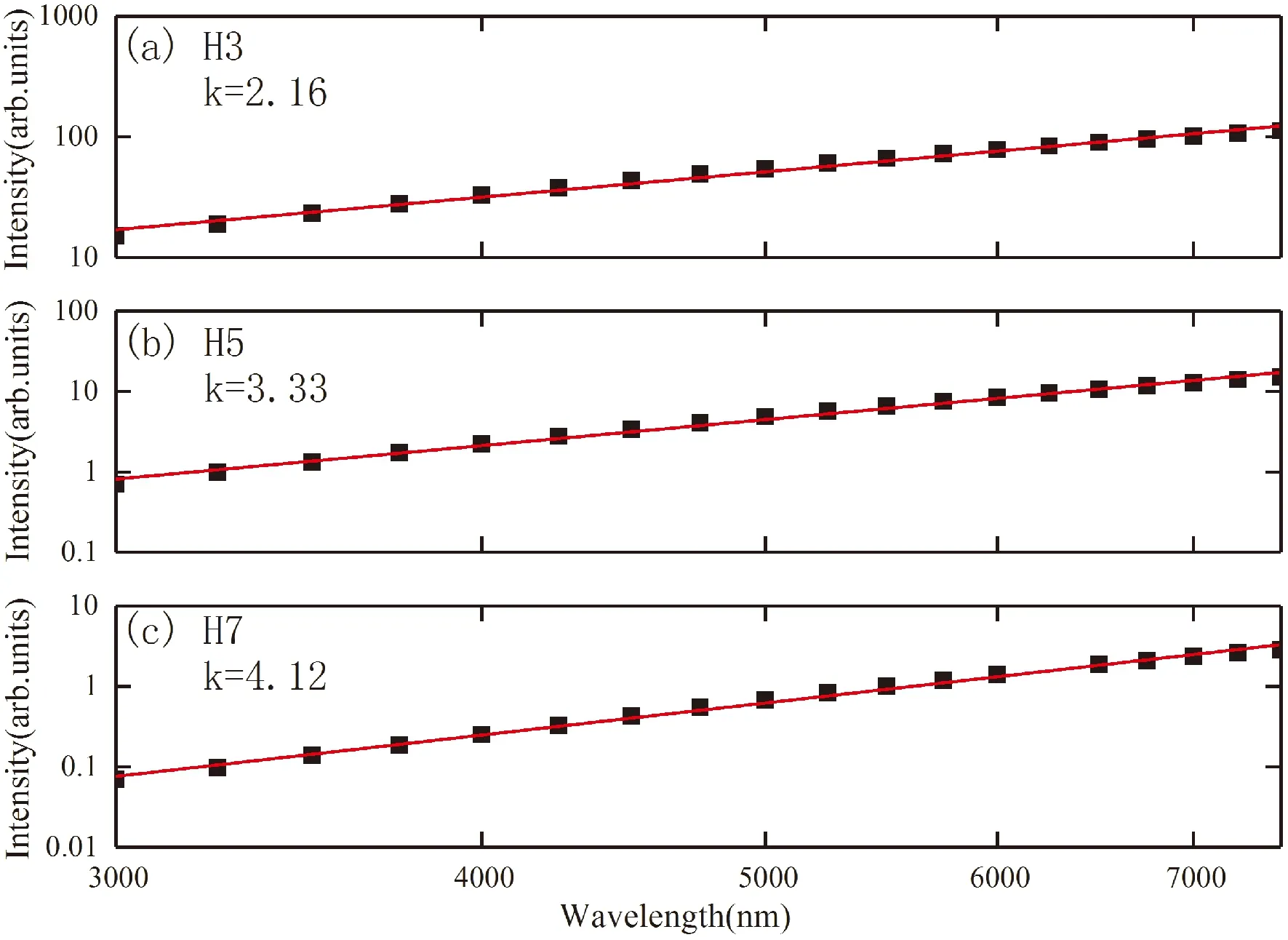
图2 低阶谐波强度随激光波长的变化, (a)第3阶，(b)第5阶，(c)第7阶(图中方块是计算结果，实线是拟合结果)，激光强度I=2.2×1011W/cm2Fig. 2 Wavelength dependence of the low-order harmonic yield ΔY when the laser intensity I=2.2×1011W/cm2(a)H3 (b)H5 (c)H7

由图可以看出，当激光强度保持不变，每一阶谐波的强度都随波长的增加而增加，如果将图中计算的数据进行拟合，拟合后得到第3阶、第5阶和第7阶的谐波强度ΔY与波长λ的关系为InΔY∝kInλ，则指数因子k分别为2.16、3.33和4.12，第7阶谐波的增加最快. 如果将激光强度增加到I=4.2×1011W/cm2时，我们进行了相同的计算和数据拟合，结果如图3所示，由图可见，其变化规律与上述规律基本相同，拟合所得的第3阶、第5阶和第7阶的指数因子分别为1.54、2.55、和2.83，与激光强度I=2.2×1011W/cm2相比，谐波强度随激光波长增加仍然增加，不过增加的强度有所放缓.

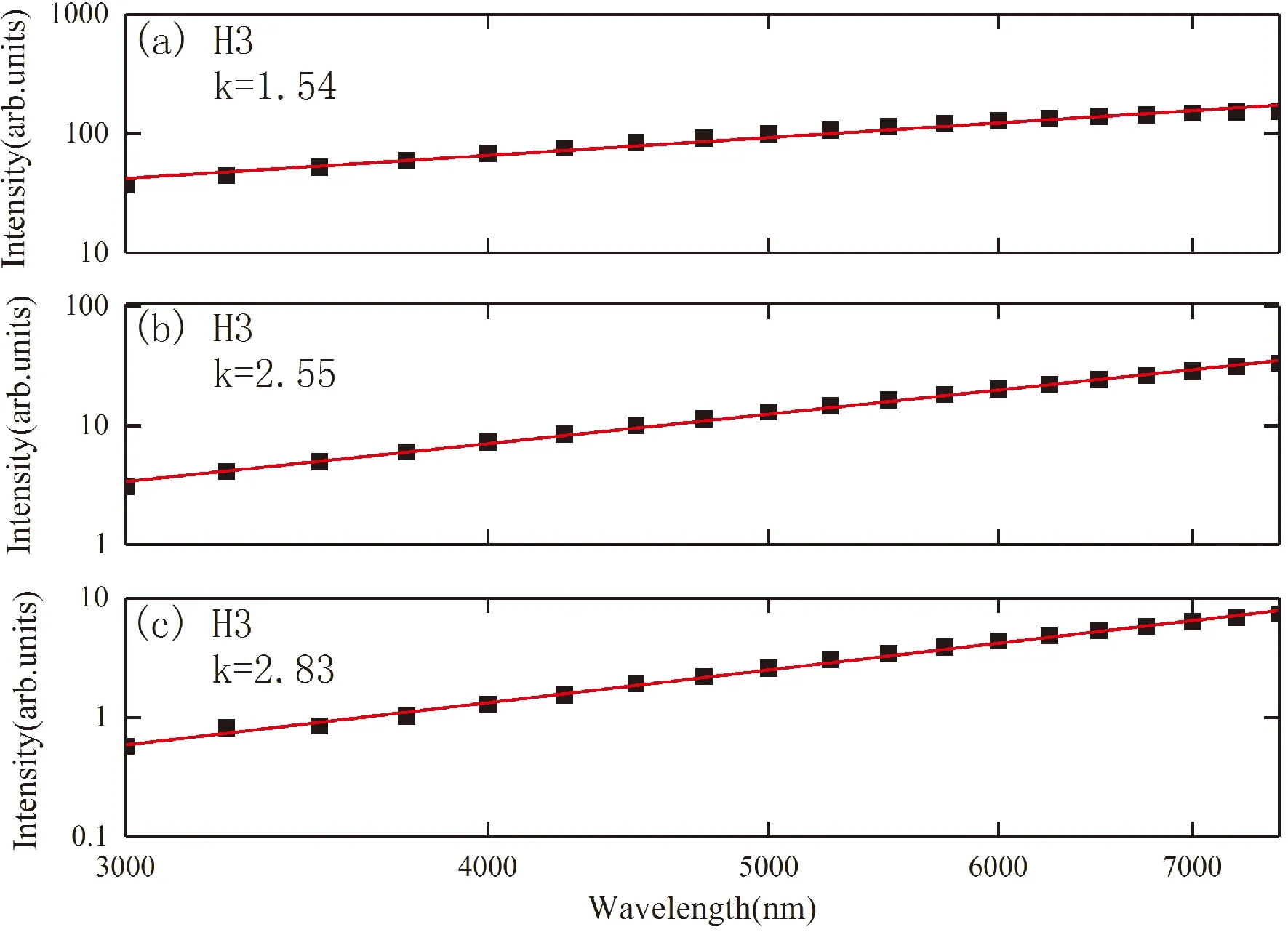
图3 低阶谐波强度随激光波长的变化, (a)第3阶，(b)第5阶，(c)第7阶(图中方块是计算结果，实线是拟合结果)，激光强度I=4.2×1011W/cm2Fig. 3 Wavelength dependence of the low-order harmonic yield ΔY when the laser intensity I=4.2×1011W/cm2(a)H3 (b)H5 (c)H7

为了理解不同波长激光驱动晶体发射低阶谐波强度随波长变化的原因，我们选择对3000 nm和6000 nm波长的激光驱动下晶体发射低阶谐波谱进行分析，将激光驱动下晶体内的电流进行小波变换[6]，得到了两种情况下低阶谐波的时间-频率图，如图4所示. 从图4(a)可以看出：第3阶谐波有明显发射是从t=-30fs开始，持续时间约为60fs，第5阶谐波有明显发射开始于t=-20fs、持续时间约为40fs；第7阶谐波的初始发射时刻t=-15fs、持续时间约为30fs；而从图4(b)的结果来看，当λ=6000 nm时，相对于3000 nm激光驱动时，低阶谐波的发射时间都有所延长，如第3阶谐波有明显发射从t=-40fs开始，持续时间约为80fs，对于第5阶和第7阶谐波发射持续时间也都比3000 nm激光驱动情况下有所延长. 对于激光强度不太强的情况下，一般由微扰理论可以计算出跃迁几率，对同一体系其跃迁几率只与激光强度有关，而与激光波长无关，在激光强度差别不大情况下，如果跃迁持续的时间越长，谐波的发射就越强. 由此可见，长波驱动情况下低阶谐波强度较高的原因是发射时间较长.

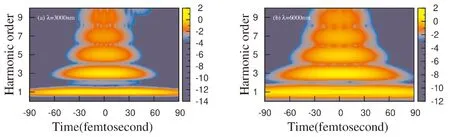
图4 图1中的低阶谐波时-频分析图 (a) 波长3000 nm，(b)波长6000 nmFig. 4 Time-frequency analysis of HHG in Fig.1. Laser wavelengths (a)3000 nm and (b)6000 nm

那么，低阶谐波的发射时间与波长为什么会有依赖关系呢？下面我们对此进行定性的分析：晶体发射谐波的机理对于不同的能区，其发射机理有所不同，已有的研究表明，对于平台区的谐波来说，主要是带间电流的贡献，而对低阶谐波而言，主要来源于带内电流的贡献，晶体中的电子-空穴对在激光场的作用下发生布洛赫震荡产生带内电流，带内电流主要是发射低阶谐波. 上述是电流观点对低阶谐波发射的解释，同样，我们也可以用系统在周期性外场驱动下的弗洛盖理论给与解释，实际上发射的低阶谐波是同一能带在激光场中形成了许多缀饰态能级，这些能级可以表示为E0±nħω[21]，其中E0为体系无外场的能量，ω是入射激光单个光子的能量，这些缀饰态能级间隔就是入射激光单个光子的能量，当电子在这些缀饰态之间跃迁时需要满足宇称守恒，所以只有是激光光子奇数倍的谐波才有发射. 因此，我们可以通过激光光子的能量大小与价带的能量变化关系就会发现：在激光脉冲宽度相同的情况下，当激光波长较长时，即入射激光光子能量较小时，低阶谐波其发射的持续时间会较长. 为此，我们需要计算晶体价带的能带能量随时间的变化，即休斯敦态能量随时间的变化. 通过对不同时刻的体系哈密顿量进行对角化，我们计算了激光波长分别为3000 nm和6000 nm时k=0处最高价带的能量随时间的变化(价带的初始能量为-0.098 a.u.)，图5给出了不同波长驱动下最高价带(k=0处)的能量随时间的变化图. 图中还用虚线给出了的能量间隔，每一能量间隔刚好是入射激光单个光子的能量(相当于弗洛盖能级的分裂). 从图5(a)中可以看出，当激光波长为3000 nm时，能够满足第3阶谐波能量关系的发射时刻约为-25 fs，而对于6000 nm激光驱动时，满足第3阶谐波发射条件的时刻约为-32 fs，显然，这时的发射持续时间较长；同理，对于第5阶和第7阶谐波的情况也是如此，如图中所标示的5ω和7ω对应箭头的位置.

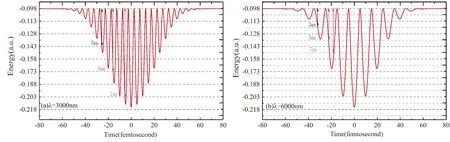
图5 激光驱动下晶体价带能量随时间的变化. 图中虚线间隔表示激光单个光子的能量, (a)波长3000 nm, (b)波长6000 nmFig. 5 The change of valence band energy with time driven by laser. The dot line interval is the energy of a single photon of laser, wavelengths (a) 3000 nm and (b)6000 nm

由上面的分析可以理解晶体发射的低阶谐波随驱动激光波长的增加而增强的主要原因在与其发射机理与晶体发射谐波的平台区域变化规律不同的原因主要是发射机理的不同，平台区域的发射过程涉及到电子波包的演化，而低阶谐波的发射可以看作是缀饰态之间的跃迁形成的，相应的发射过程没有涉及到波包的演化，当激光脉冲宽度相同时，对同一阶谐波而言，波长较长时其发射时间会有所增加，导致谐波发射强度的提高.

需要指出的是，在我们的计算中，选取的激光脉冲的宽度是相同的，这样对于不同的波长，其驱动激光的脉冲能量差别较小，对于不同的波长而言，会导致激光的周期有所不同，这样干涉效应会引起低阶谐波的宽度不同(图1可以看出)，如果考虑相同周期的激光脉冲驱动晶体，对于不同的波长而言，则会导致入射的脉冲能量不同，这样可比性就会有所下降，因此，如果扣除干涉效应引起计算低阶谐波的强度误差，所得到的k值会有所减小.

4 结 论

本文通过数值求解一维周期势中的电子在激光场中的含时薛定谔方程，研究了晶体发射低阶谐波的强度与驱动激光波长的依赖关系.研究结果表明，在激光的强度和脉宽一定的情况下，晶体产生的第3阶、第5阶和第7阶的谐波发射强度会随激光波长的增加而增加，这与晶体发射高次谐波平台区域的变化规律有所不同. 为探究出现这一结果的原因，我们对两个不同波长激光驱动下晶体发射低阶谐波的性质进行了分析，通过时-频分析图，结合晶体发射低阶谐波的机理，给出了发生这种现象的原因主要是当激光的波长较长时，低阶谐波的发射时间会有所延长，从而使得发射的强度提高，这与晶体发射高次谐波平台区域的情况有所不同，在平台区域，当驱动激光波长变长时，发射时间也会延长，但是由于电子波包在激光场的演化时间也会增加而导致波包扩散较为严重，从而使得发射强度降低.