外加电场和磁场对外尔半金属能带结构的调控*
2023-12-22罗淑珍廖文虎鲍海瑞
罗淑珍,廖文虎,鲍海瑞
(吉首大学物理与机电工程学院,湖南 吉首 416000)
1928年,英国物理学家狄拉克提出了著名的狄拉克方程[1],该方程能够描述具有相对论效应的电子波动行为.1929年,德国物理学家外尔在理论上预言:质量为0时的狄拉克方程可以描述一对具有相反手性的外尔费米子[2].自从外尔费米子的概念被引入到凝聚态物理领域以来,以准粒子激发形式存在的外尔半金属就受到了学者的广泛关注.外尔半金属具有拓扑非平庸的线性能带特征和相对论性电子行为,因而又被称为“三维的石墨烯”,其在纳米电子器件领域具有广阔的应用前景.
经过学者的不懈努力,近年来,外尔半金属在理论和实验研究方面都取得了许多重要进展.比如:2011年,万贤纲等[3]基于具有烧绿石结构的铱氧化物体系,最早研究了磁性外尔半金属的拓扑电子态和费米弧表面态,这一研究成为外尔半金属后续研究的重要起点;同年,徐刚等[4]基于第一性原理计算,首次提出了在铁磁半金属HgCr2Se4中受拓扑保护的双外尔费米子概念;2015年,翁红明等[5]基于第一性原理计算,从理论上预言了外尔半金属砷化钽TaAs的存在;同年,这一重要的外尔半金属材料在实验上得以成功制备[6],于是外尔半金属迅速成为凝聚态物理和材料科学领域的研究热点[7-11].外尔半金属具有许多新奇的物理特性,如三维无能隙线性色散能带结构[3]、手性异常现象[12]、负磁阻效应[13]和手性朗道能级[14-15]等.近年来,关于外场调控外尔半金属的量子输运性质引起了学者的密切关注[16-17].目前,外加磁场调控外尔半金属能带结构已有较多研究报道[14-15,18],值得注意的是,外加电场也可调控外尔半金属能带结构[19].在电场和磁场的共同作用下,外尔半金属展现出更多有趣的物理现象[20].基于此,笔者拟利用紧束缚近似下的低能有效哈密顿模型,研究外加电场、外加磁场及外加电场和磁场作用下的外尔半金属电子能带结构,旨在为外尔半金属电子能带结构的调控提供参考.
1 模型与方法
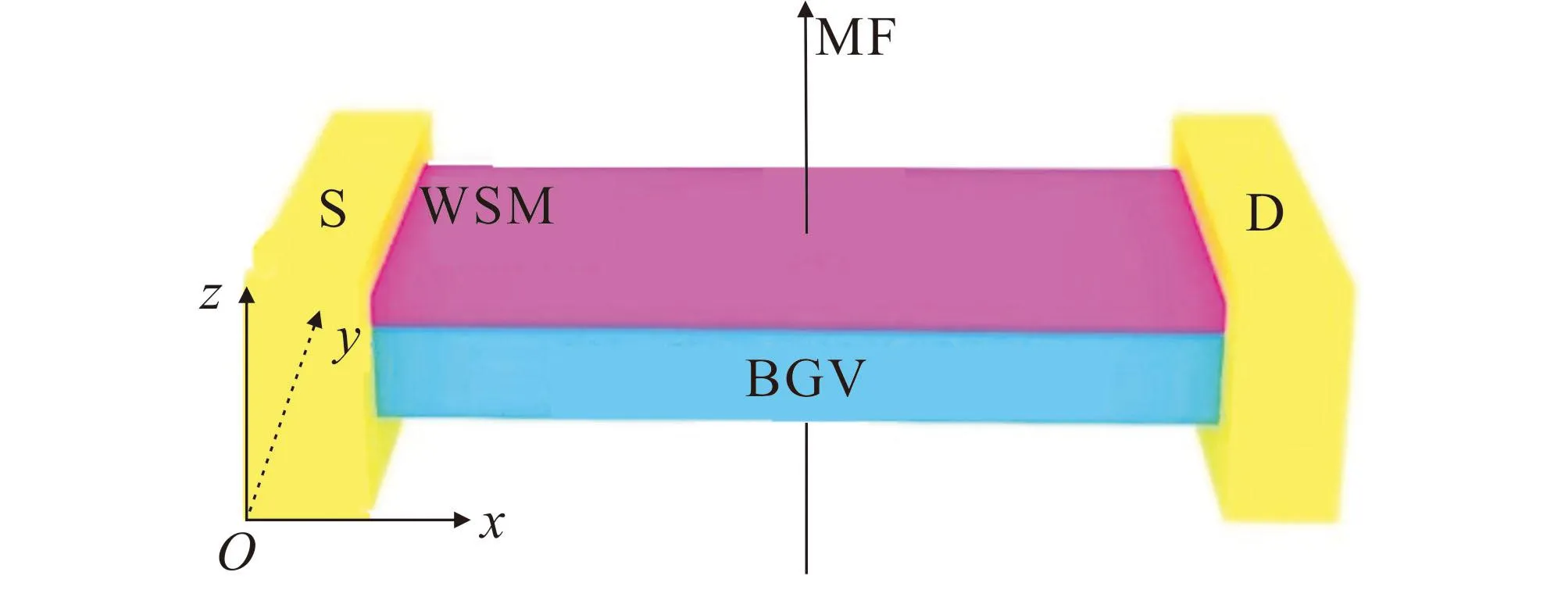
图1 基于外尔半金属的纳米场效应晶体管Fig. 1 Schematic Representation of the Weyl Semimetal Based Field Effect Transistor
构建一个基于外尔半金属的纳米场效应晶体管模型,如图1所示.从图1可知,模型由金属源极(S)、漏极(D)、可调制背电极(BGV)和外尔半金属(WSM)组成,模型中心区域受到外加垂直磁场(MF)作用.
基于紧束缚近似下的低能有效理论[21-23],外尔半金属的哈密顿量
H=hxσx+hyσy+hzσz
(1)
其中:
hx=2t1sinkx;hy=-2t1sinky;
hz=2t2(2-cos (kx-ky)-cos (kx+kz))+2t3coskz.
这里ti(i=1,2,3)为跃迁振幅,t1,t2,t3分别取4,2,1 eV.对体系哈密顿量进行对角化,可得色散关系
本研究中,一共考虑外加电场、外加磁场及同时外加电场和磁场3种条件:
(1)当仅在z方向上施加电场时,体系哈密顿量
(2)
其中电场引起的能量U=eEzLz.这里Ez为电场强度,Lz为系统在z方向上的厚度.对(2)式中的哈密顿量进行对角化,可得色散关系
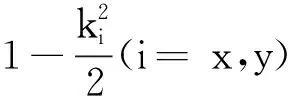
在朗道规范下,引入矢势A=(0,Bx,0)到体系哈密顿量中,即
Πi=ћki-eAi/ci=x,y.
(3)
对(3)式中的哈密顿量进行对角化,得到色散关系
(3)当在z方向上同时施加电场和磁场时,体系的有效哈密顿量
(4)
对(4)式中的哈密顿量进行对角化,可得色散关系
2 结果
2.1 外加电场对外尔半金属电子能带结构的调控
外加正向电场对外尔半金属电子能带结构的调控效果如图2所示.
设沿竖直向上方向施加的电场为外加正向电场.从图2(a)可知,无外加电场作用下,导带和价带之间的能隙为0,说明此时的外尔点出现在布里渊区中的(0,0,±π/2)动量点处.从图2(b)可知,当正向电场引起的能量为1 eV时,虽然导带和价带之间的能隙为仍然为0,但是外尔点的位置却向布里渊区的边界移动,由(0,0,±π/2)动量点处移动至(0,0,±2.09)动量点处.从图2(c)可知,当正向电场引起的能量增大到2 eV时,外尔点移动至布里渊区的边界(0,0,±π)处.从图2(d)可知,当正向电场引起的能量增大至3 eV时,导带和价带之间形成大小为2 eV的能隙,此时体系外尔点消失.随着电场引起的能量的逐渐增大,体系的导带和价带逐渐远离费米能级,从而实现由外尔半金属到半导体或绝缘体的转变.
外加负向电场对外尔半金属电子能带结构的调控效果如图3所示.

图3 不同外加负向电场作用下的外尔半金属电子能带结构Fig. 3 Band Structure of Weyl Semimetals in Different Negative Electric Fields
从图3(a)可知,无外加负向电场作用下,导带与价带之间的能隙为0,此时,外尔点位于(0,0,±π/2)动量点处.从图3(b)可知,当外加负向电场引起的能量为1 eV时,导带和价带之间的能隙仍然为0,外尔点逐渐向布里渊区中心移动,由(0,0,±π/2)动量点处移动至(0,0,±1.04)动量点处.从图3(c)可知,当负向电场引起的能量增大至2 eV时,外尔点移动至布里渊区中心.从图3(d)可知,当负向电场引起的能量进一步增大至3 eV时,导带和价带之间形成大小为2 eV的能隙.与正向电场作用情形类似,随着负向电场引起的能量逐渐增大,体系的导带和价带逐渐远离费米能级,进而实现从外尔半金属到半导体或绝缘体的转变.
2.2 外加磁场对外尔半金属电子能带结构的调控
外加磁场对外尔半金属电子能带结构的调控效果如图4所示,图中实线表示费米能级.
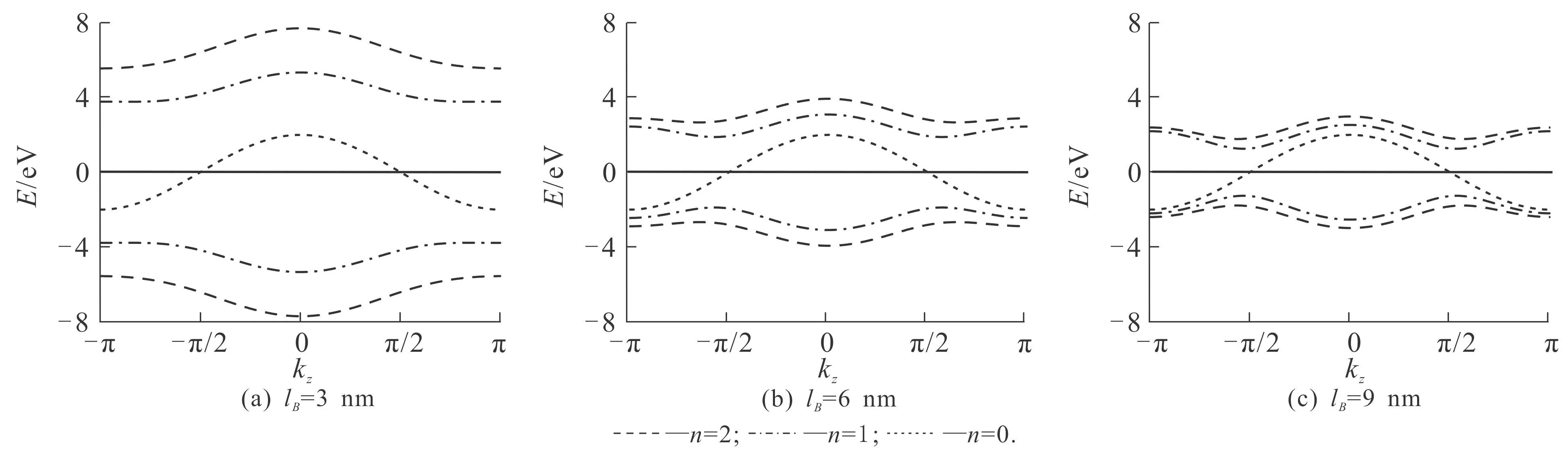
图4 不同外加磁场作用下的外尔半金属电子能带结构Fig. 4 Band Structure of Weyl Semimetals in Different Magnetic Fields
外尔半金属在垂直磁场作用下可以形成分立的朗道能级[14-15].从图4(a)可知,lB=3 nm时,外尔半金属在-8~8 eV能量范围内存在5支分立的朗道能级,即1支标注n=0、2支标注n=1和2支标注n=2的子带.n=0子带能量最低点(Emin=-2 eV)和最高点(Emax=2 eV)分别在布里渊区的kz=±π和kz=0处,位于费米能级附近的能带展宽(Emax-Emin)为4 eV.n=0子带穿过费米能级,因此体系呈现出半金属性特征.处于费米面以上的n=1和n=2子带能量最高点均位于布里渊区的kz=0动量点处,能量最低点分别位于kz=±2.03和kz=±2.66处.处于费米面以下的n=1和n=2子带能量最高点分别位于kz=±2.03和kz=±2.66处,能量最低点均位于布里渊区的kz=0动量点处.需要指出的是,n=1和n=2时的导带与价带是关于费米能级对称的,能带展宽分别为0.98 eV和1.21 eV,n=1和n=2时的导带与价带在kz=±π处的能隙分别为7.86 eV和10.68 eV,而在kz=0处的能隙分别为9.50 eV和13.08 eV.
从图4(b)可知,当lB增加至6 nm时,与图4(a)中各子带相比,除了n=0子带没有变化外,其余4支子带均向费米能级靠近.处于费米面以上的n=1和n=2子带的能量最高点仍然位于布里渊区kz=0处,能量最低点却向布里渊区中心靠近,分别位于kz=±1.68和kz=±1.79动量点处.处于费米面以下的n=1和n=2价带的能量分布与导带的关于费米能级对称.n=1和n=2时的导带与价带能带展宽分别为1.02 eV和0.95 eV.图4(b)中各子带的导带与价带间能隙均比图4(a)中相应子带的导带与价带间能隙小.n=1和n=2子带在kz=±π处的能隙分别为5.18 eV和6.18 eV,在kz=0处的能隙分别为5.82 eV和7.24 eV.
从图4(c)可知,当lB进一步增加至9 nm时,与lB=3 nm和lB=6 nm的结果相比,处于费米面以上的n=1和n=2子带的能量最高点仍在kz=0动量点处,能量最低点均进一步向布里渊区中心靠近,分别位于布里渊区的kz=±1.62和kz=±1.67处.此时,n=1和n=2的导带与价带均向费米能级靠近,能带展宽分别为1.19 eV和1.05 eV.n=1子带在kz=±π和kz=0处的能隙分别为4.56 eV和4.90 eV,而n=2子带的相应能隙分别为5.06 eV和5.66 eV.
2.3 同时外加电场和磁场对外尔半金属电子能带结构的调控
在lB保持3 nm不变的条件下,通过外加正向(负向)电场来调控外尔半金属的能带结构,调控效果如图5所示.


图5 不同外加电场作用下的外尔半金属电子能带结构(lB=3 nm)Fig. 5 Band Structure of Weyl Semimetals in Different Electric Fields at Magnetic Length lB=3 nm
当不施加电场时,n=0子带与费米能级的交点在布里渊区kz=±π/2处,此时体系呈现出半金属性特征(图4(a)).从图5(a)可知,当外加正向电场引起的能量增大至1 eV时,与图4(a)中各子带相比,n=0子带与费米能级的交点靠近布里渊区边界,同时在能级上具有从部分占据的价带转变为第一导带的趋势,n=0子带的能量最高点(3 eV)和最低点(-1 eV)分别位于布里渊区的kz=0和kz=±π处,能带展宽为4 eV.处于费米面以上的n=1和n=2子带能量最高点均位于布里渊区kz=0处,能量最低点均呈现出向布里渊区边界靠近的趋势,分别位于kz=±2.83和kz=±π处.n=1和n=2时的导带与价带在kz=±π处的能隙分别为7.54 eV和10.78 eV,在kz=0处的能隙分别为10.84 eV和14.32 eV.此时,n=1和n=2子带的能带展宽分别为1.65 eV和1.77 eV.
从图5(b)可知,当外加正向电场引起的能量增大至2 eV时,与图5(a)中各子带相比,n=0子带与费米能级刚好相切于布里渊区的边界,因此n=0子带转变为体系的第一导带,其能带最高点和最低点的能量分别为4 eV和0 eV,其能带展宽为4 eV.此时第一导带(n=0)和第一价带(n=1)之间的直接带隙为3.87 eV.处于费米面以上的n=1和n=2子带的能量最高点均位于布里渊区kz=0处,最低点均位于布里渊区kz=±π处.n=1和n=2时的导带与价带在kz=±π处的能隙分别为7.74 eV和11.24 eV,在kz=0处的能隙分别为12.34 eV和15.72 eV.此时,n=1和n=2子带的能带展宽分别增大至2.30 eV和2.24 eV.
从图5(c)可知,当外加正向电场引起的能量进一步增大至3 eV时,与图5(b)中各子带相比,n=0子带位于费米能级之上,其能带最高点和最低点的能量分别为5 eV和1 eV,能带展宽大小保持不变,仍为4 eV.处于费米面以上的n=1和n=2子带的能量最高点均位于布里渊区kz=0处,能量最低点均位于布里渊区边界.n=1和n=2时的导带与价带在kz=±π处的能隙分别为8.44 eV和12.02 eV,在kz=0处的能隙分别为13.98 eV和17.24 eV,n=1和n=2子带的能带展宽分别增大至2.77 eV和2.61 eV.图5(a)~(c)说明,n=0子带与费米能级的交点随着正向电场引起的能量的增大而不断地向布里渊区边界移动,当正向电场引起的能量增大到一定程度时,可以实现半金属向半导体或绝缘体的转变.
从图5(d)可知,当外加负向电场引起的能量为1 eV时,与图4(a)中各子带相比,n=0子带与费米能级的交点(kz=±1.04)靠近布里渊区中心,其能带最高点和最低点分别位于kz=0和kz=±π处,能带展宽为4 eV.处于费米面以上的n=1和n=2子带的能量最高点分别位于布里渊区kz=±π和kz=0处,能量最低点分别位于布里渊区kz=±1.51和kz=±1.97处.n=1和n=2时的导带与价带在kz=±π处的能隙分别为8.64 eV和10.94 eV,在kz=0处的能隙分别为8.44 eV和12.02 eV.
从图5(e)可知,当外加负向电场引起的能量增大至2 eV时,与图5(d)中各子带相比,n=0子带与费米能级刚好相切于布里渊区中心,此时部分占据的n=0子带变为完全占据的价带.第一导带(n=1)和第一价带(n=0)之间的全局能隙为3.77 eV.处于费米面以上的n=1和n=2子带的能量最高点均位于布里渊区的kz=±π处,能量最低点分别位于布里渊区kz=±0.97和kz=±1.45处.n=1和n=2时的导带与价带在kz=±π处的能隙分别为9.78 eV和11.56 eV,在kz=0处的能隙分别为7.74 eV和11.24 eV.
从图5(f)可知,当外加负向电场引起的能量继续增大至3 eV时,与图5(e)中各子带相比,n=0子带移动至费米能级之下,其能带最高点和最低点的能量分别为-1 eV和-5 eV.对于n=1和n=2子带,其能带最高点均位于布里渊区kz=±π处,最低点分别位于布里渊区kz=0和kz=±0.92处.n=1和n=2时的导带与价带在kz=±π处的能隙分别为11.16 eV和12.46 eV,在kz=0处的能隙分别为7.54 eV和10.78 eV.n=1和n=2子带的能带展宽分别为1.81 eV和0.90 eV.图5(d)~(f)说明,n=0子带与费米能级的交点随着负向电场引起的能量的增大而不断地向布里渊区中心移动,当负向电场引起的能量增大到一定程度时,n=0子带与费米能级相切于布里渊区中心,即kz=0动量点处,且随着负向电场引起的能量的进一步增大,n=0子带向远离费米能级的方向移动,从而实现了半金属向半导体或绝缘体的转变.
在lB保持6 nm不变的条件下,通过外加正向(负向)电场来调控外尔半金属的能带结构,调控效果如图6所示.

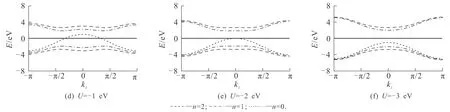
图6 不同外加电场作用下的外尔半金属电子能带结构(lB=6 nm)Fig. 6 Band Structure of Weyl Semimetals in Different Electric Fields at Magnetic Length lB=6 nm
从图6(a)可知,当外加正向电场引起的能量为1 eV时,与图4(b)中各子带相比,处于费米面以上的n=1和n=2子带的能量最高点均位于布里渊区kz=0处,最低点均靠近布里渊区边界,其能带展宽分别增大至1.84 eV和1.69 eV.在kz=0处,导带和价带均逐渐远离费米能级,n=1和n=2时的导带与价带之间的带隙分别为7.46 eV和8.72 eV.在kz=±π处,导带和价带均靠近费米能级,n=1和n=2时的导带与价带之间的带隙分别减小至4.08 eV和5.44 eV.
从图6(b)可知,当外加正向电场引起的能量增大至2 eV时,与图6(a)中各子带相比,体系呈现出直接带隙半导体特征,全局能隙为1.90 eV.n=1和n=2子带的能带展宽继续增大至2.72 eV和2.48 eV.在kz=0处,导带和价带均继续向深能级方向移动,n=1和n=2时的导带与价带之间的带隙继续增大至9.24 eV和2 eV.在kz=±π处,体系的导带和价带均继续向费米能级靠近,n=1和n=2时的导带与价带之间的带隙分别减小至3.80 eV和5.40 eV.
从图6(c)可知,当外加正向电场引起的能量进一步增大至3 eV时,与图6(b)中各子带相比,n=0子带移动至费米能级之上,第一导带和第一价带之间的能隙为3.25 eV.n=1和n=2子带的能带展宽分别增大至3.30 eV和3.03 eV.在kz=0处,导带和价带均进一步向远离费米能级方向移动,n=1和n=2时的导带与价带之间的能隙分别增大至11.10 eV和12.12 eV.在kz=±π处,导带和价带也向靠近费米能级方向移动,n=1和n=2时的导带与价带之间的带隙分别增大至4.50 eV和6.06 eV.图6(a)~(c)说明,对于n=1和n=2子带,在kz=0处,其导带和价带随着正向电场引起的能量的增大而逐渐向深能级方向移动.然而,在kz=±π处,n=1和n=2时的导带与价带随着正向电场引起的能量的增大先向费米能级靠近,再远离费米能级而向深能级方向移动.n=1和n=2子带的能带展宽随着正向电场引起的能量的增大而不断变宽.
从图6(d)可知,当外加负向电场引起的能量为1 eV时,与图4(b)中各子带相比,处于费米面以上的n=1和n=2子带的能量最高点均位于布里渊区边界处,最低点分别位于布里渊区kz=±1.14和kz=±1.27处,能带展宽分别增大至1.47 eV和1.03 eV.在kz=0处,导带和价带均靠近费米能级,n=1和n=2时的导带与价带之间的带隙分别减小至4.50 eV和6.06 eV.在kz=±π处,导带和价带均向深能级方向移动,n=1和n=2时的导带与价带之间的带隙分别增大至6.72 eV和7.38 eV.
从图6(e)可知,当外加负向电场引起的能量增大至2 eV时,体系呈现出间接带隙半导体特征,全局带隙为1.89 eV.与图6(d)中各子带相比,n=1和n=2子带的能量展宽分别增大至2.34 eV和1.78 eV.在kz=0处,导带和价带均继续向靠近费米能级方向移动,n=1和n=2时的导带与价带之间的带隙均继续减小,分别减小至3.78 eV和5.40 eV.在kz=±π处,体系的导带和价带均继续向深能级方向移动,n=1和n=2时的导带与价带之间的带隙分别为8.44 eV和8.88 eV.
从图6(f)可知,当外加负向电场引起的能量增大到3 eV时,与图6(e)中各子带相比,n=0子带移动至费米能级之下,第一导带和第一价带之间的能隙为3.04 eV.n=1和n=2子带的能带展宽分别增大至3.10 eV和2.55 eV.在kz=0处,n=1和n=2时的导带与价带之间的能隙分别为4.08 eV和5.40 eV.在kz=±π处,导带和价带进一步向深能级方向移动,n=1和n=2时的导带与价带之间的带隙分别增大至10.28 eV和10.56 eV.图6(d)~(f)说明,n=1和n=2子带的能带展宽随着外加负向电场引起的能量的增大而不断变宽.在kz=0处,导带和价带随着外加负向电场引起的能量的增大先向费米能级靠近,再远离费米能级而向深能级方向移动.但在kz=±π处,导带和价带随着外加负向电场引起的能量的增大而不断向深能级方向移动.
在lB保持9 nm不变的条件下,通过外加正向(负向)电场来调控外尔半金属的能带结构,调控效果如图7所示.
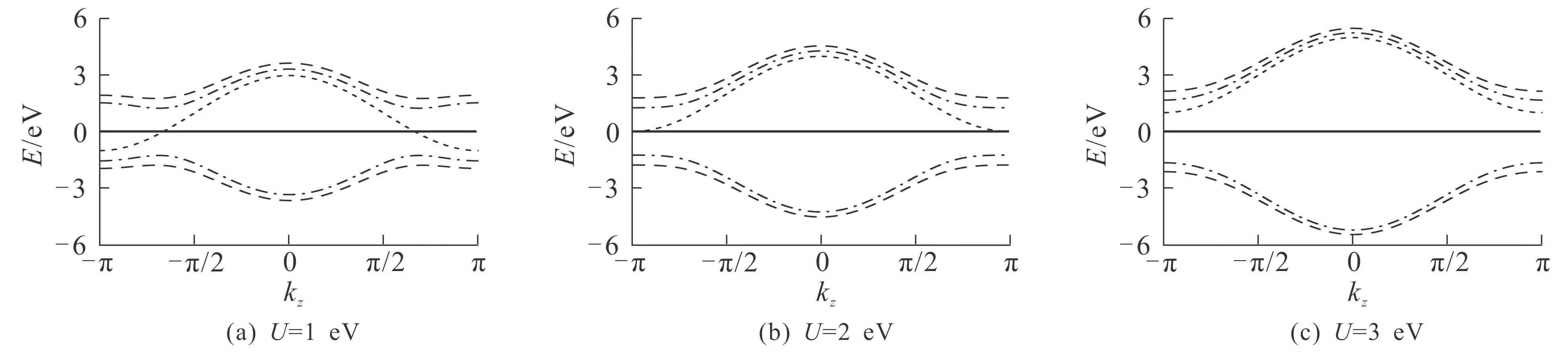

图7 不同外加电场作用下的外尔半金属电子能带结构(lB=9 nm)Fig. 7 Band Structure of Weyl Semimetals in Different Electric Fields at Magnetic Length lB=9 nm
从图7(a)可知,当外加正向电场引起的能量为1 eV时,与图4(c)中各子带相比,处于费米面以上的n=1和n=2子带的能量最高点均位于布里渊区kz=0处,能量最低点分别位于kz=±2.15和kz=±2.20处.n=1和n=2子带的能带展宽分别增大至2.08 eV和1.88 eV,在kz=0处,n=1和n=2时的导带与价带之间的能隙分别为6.68 eV和7.32 eV,在kz=±π处,n=1和n=2时的导带与价带之间的能隙分别为3.10 eV和3.90 eV.
从图7(b)可知,随着外加正向电场引起的能量的增大(2 eV),体系从半金属态转变为直接带隙半导体态,全局带隙为1.26 eV.与图7(a)中各子带相比,n=1和n=2子带的能带展宽分别增大至3.03 eV和2.77 eV.在kz=0处,体系的导带和价带均向深能级方向移动,n=1和n=2时的导带与价带之间的带隙分别为8.58 eV和9.12 eV.在kz=±π处,体系的导带和价带均继续向费米能级靠近,n=1和n=2时的导带与价带之间的带隙分别减小至2.52 eV和3.58 eV.
从图7(c)可知,当外加正向电场引起的能量进一步增大至3 eV时,与图7(b)中各子带相比,n=0子带移动至费米能级之上,第一导带和第一价带之间的带隙为1.70 eV.随着正向电场引起的能量的增大,n=0子带从部分占据的第一价带变为非占据的第一导带,实现了体系中半金属向半导体的转变.
从图7(d)可知,当外加负向电场引起的能量为1 eV时,与图4(c)中各子带相比,处于费米面以上的n=1和n=2子带的能量最高点均位于布里渊区kz=±π处,能量最低点均向布里渊区中心移动,分别移动至kz=±1.10和kz=±1.18处.n=1和n=2子带的能带展宽分别为1.91 eV和1.54 eV,在kz=0处,体系的导带和价带均靠近费米能级,n=1和n=2时的导带与价带之间的能隙分别为3.34 eV和4.28 eV.在kz=±π处,体系的导带和价带均向深能级方向移动,n=1和n=2时的导带与价带之间的能隙分别增大至6.32 eV和6.64 eV.
从图7(e)可知,当外加负向电场引起的能量增大至2 eV时,体系呈现出半导体特征,全局带隙为1.26 eV.与图7(d)中各子带相比,n=1和n=2子带的能带展宽分别为2.84 eV和2.42 eV.在kz=0处,n=1和n=2时的导带与价带之间的能隙分别为2.52 eV和3.58 eV.在kz=±π处,体系的导带和价带均继续向深能级方向移动,n=1和n=2时的导带与价带之间的能隙分别为8.20 eV和8.40 eV.
从图7(f)可知,当外加负向电场引起的能量增大至3 eV时,与图7(e)中各子带相比,n=0子带移动至费米能级之下,第一导带和第一价带之间的直接带隙增大至2.55 eV.n=1和n=2子带的能带展宽分别为3.51 eV和3.17 eV.在kz=0处,n=1和n=2时的导带与价带之间的带隙分别为3.10 eV和3.90 eV.在kz=±π处,体系的导带和价带向深能级方向移动,n=1和n=2时的导带与价带之间的带隙分别增大至10.12 eV和10.24 eV.
3 结论
笔者利用紧束缚近似下的低能有效哈密顿模型,研究了外加电场、外加磁场及同时外加电场和磁场作用下外尔半金属的电子能带结构.结果显示,外加电场、外加磁场及外加电场和磁场均可有效调控外尔半金属的电子能带结构.在仅有外加正向(负向)电场作用下,外尔半金属中的外尔点随着电场引起的能量的增大而逐渐向布里渊区边界(布里渊区中心)移动,并在适当的外加电场下可以实现半金属向半导体或绝缘体的转变.在仅有外加垂直磁场作用下,外尔半金属可以形成分立的朗道能级,n=0子带不随着磁长度的增加而变化,n=1和n=2子带随着磁长度的增加不断向费米能级靠近且相同指标导带和价带间的能隙不断减小.在保持磁长度不变的条件下,体系的外尔点随着外加正向(负向)电场引起的能量的增大逐渐向布里渊区边界(布里渊区中心)移动,当电场引起的能量增大到一定程度时,n=0子带由部分占据的价带变为第一导带或完全占据的第一价带,实现了半金属向半导体或绝缘体的转变.本研究结果可为外尔半金属的纳米电子学低功耗器件和介观逻辑器件的制备及应用提供有价值的理论参考.
