基于介质圆柱结构的复式二维光子晶体禁带研究

王媛媛，张立新，王一阳，严智煜，何晓东

(1.海南医学院医学信息学院，海口571199;2.吉林省辐射环境监督站管理科，长春130012; 3.吉林大学通信工程学院，长春130012)

基于介质圆柱结构的复式二维光子晶体禁带研究

王媛媛1，张立新2，王一阳3，严智煜3，何晓东3

(1.海南医学院医学信息学院，海口571199;2.吉林省辐射环境监督站管理科，长春130012; 3.吉林大学通信工程学院，长春130012)

为提高二维光子晶体禁带带宽或产生完全禁带，利用平面波展开法对二维正方排列介质圆柱和三角排列介质圆柱结构以及改变其晶胞形成的复式结构进行了禁带研究。研究结果表明，对于介质柱结构，实现禁带中心频率低频化的方式有两种，即增大介质柱半径和增加介质柱折射率。当采用复式结构时，一般可形成较大的TM(Transverse Magnetic)禁带，同时为TE(Transverse Electric)禁带和完全禁带的形成提供了可能。通过改变晶胞结构，破坏结构对称性是实现完全禁带的一种可行方法。

光子晶体;二维光子晶体;平面波展开法;禁带结构;完全禁带

0 引 言

近十几年来，研究人员开辟了一个崭新的研究领域-光子晶体及其应用领域，用于控制光及电磁波的传播。光子晶体［1，2］是一种周期性调整介电常数的结构，它可以产生光子禁带(PBGs:Photonic Band Gaps)光谱区，频率落在光子禁带中的光不能传播，在某种意义上，这类似于半导体中的电带隙。由于其独特的特性，光子晶体在光通信上有重要用途，如，可用它制作光子晶体微谐振腔［3］，光子晶体光开关［4］，光子晶体滤波器［5］等，这些器件对光集成起到举足轻重的作用。

相对于三维光子晶体，二维光子晶体以其制作简单而受到人们广泛的关注，并在禁带［6-16］研究方面有很多新的进展。电磁波可分解为电场矢量垂直于入射面的横电波即TE(Transverse Magnetic)波和磁场矢量垂直于入射面的横磁波即TM(Transverse Magnetic)波。在禁带研究中，人们总是希望提高TE禁带或TM禁带的带宽，或使TE禁带与TM禁带产生重叠即产生完全禁带。研究表明，二维光子晶体正方排列介质圆柱结构只存在TM禁带，降低对称性能增大带隙宽度。降低对称性的一般方法有:采用各向异性材料，改变晶胞，组员形状或晶格形状。笔者将利用改变晶胞的方法降低结构对称性，通过改变二维正方排列介质圆柱结构和二维三角排列介质圆柱结构的晶胞，研究改变后形成的二维复式结构的禁带特性。

1 理论分析

光子晶体禁带常用的计算方法有很多，如时域有限差分法、平面波展开法等。与经典的电磁理论分析方法类似，在不同外界条件下，采用不同方法往往可取得事半功倍的效果。平面波展开法概念清晰已经取得广泛的应用。将电磁场在倒格矢空间展开为平面波，以本征方程代替麦克斯韦方程组，经过求解本征方程得到其本征值，最终反映出光子晶体中电磁波的本征频率与色散之间的关系，从而得到能带结构和透射反射系数。笔者将利用该方法进行带隙计算［17］。光子晶体基本方程如下

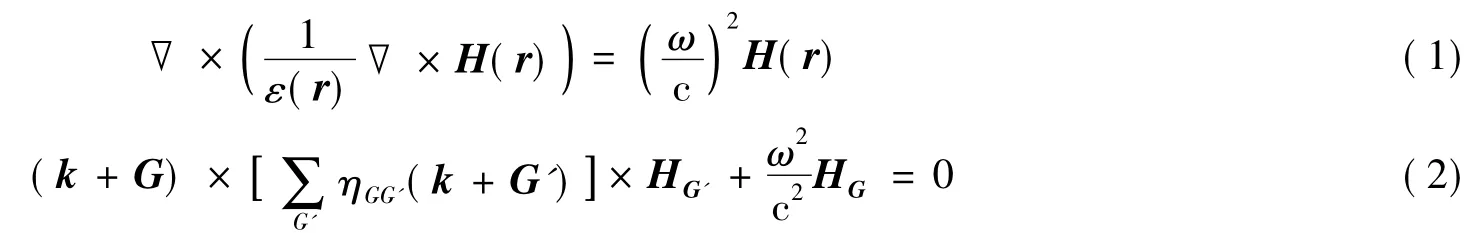
其中ε(r)为介质的介电常数，ω为电磁波角频率，c为真空中的光速。式(2)是傅里叶空间中的光子晶体基本方程的形式，是矢量式，必须将其转化成标量形式才可以进行计算。其中ηGG'=η(G-G')，而以倒格矢为自变量的η是η(r)的傅里叶变换

而介电常数倒数η(r)从原空间变换到倒格矢空间有下列式子

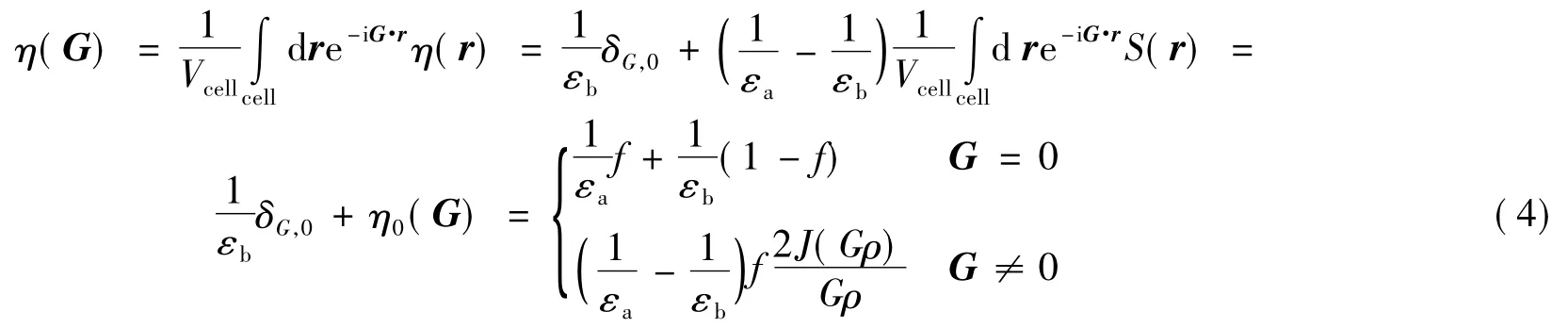
这里f是光子晶体的填充比。对任意矢量S∈xy平面，选定3个方向矢量e1(S)、e2(S)、e3(S)，关系为e1(S)、e2(S)与S垂直，e3(S)与S平行，e1(S)平行与z轴，e2(S)、e3(S)在xy平面内。这样，磁场强度H(r)可表达为

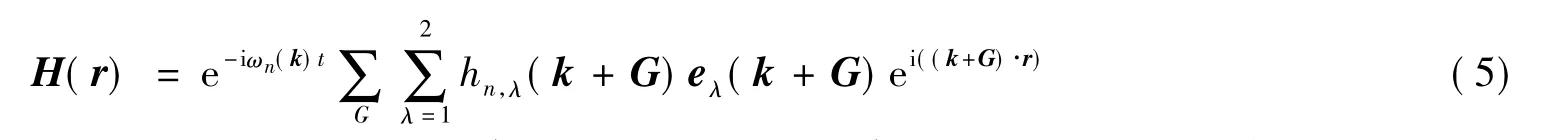
其中e1(k+G)、e2(k+G)、k+G为一组互相垂直的矢量系。式(5)代入式(2)，有下列关系

对于TM模

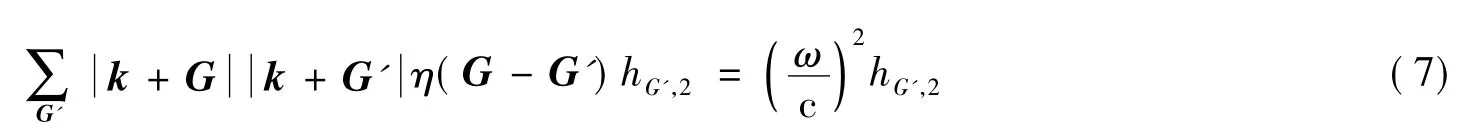
对于TE模

根据具体的折射率分布求解本征方程便可得到本征值以及本征矢值，从而确定光子晶体的禁带结构。

2 基于介质圆柱结构的复式二维光子晶体的禁带分析

以正方排列和三角排列介质圆柱结构为例，经过改变的复式二维光子晶体结构如图1所示。为了比较，笔者同时对没经过改变的二维正方排列介质圆柱结构和二维三角排列介质圆柱结构进行禁带分析。

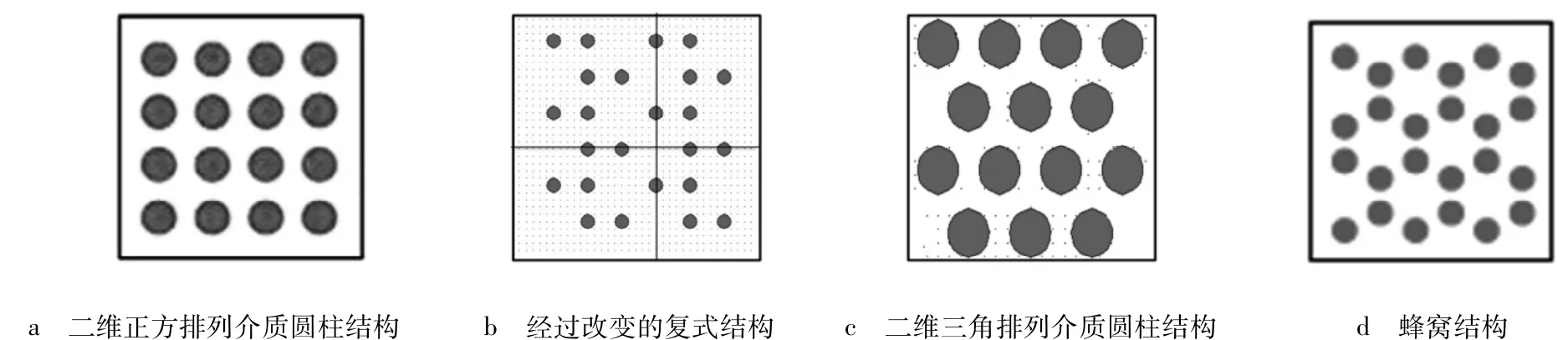
图1 二维光子晶体结构图Fig.1 The structures of two-dimensional photonic crystal

2．1 二维正方排列介质圆柱结构的禁带分析

2．1．1 介质圆柱半径对禁带的影响

借助软件仿真研究介质圆柱半径对禁带的影响。设晶格周期为a，介质圆柱折射率为3．24，在仿真过程中要保证这两个参数不变。取半径步长为0．01a，图2a为TM模禁带随着圆柱半径的变化规律。可直观看到TM模式主要存在4条禁带，每条禁带都呈枣核形分布，随着圆柱半径的增加，归一化中心频率低频化。在此以带隙率反映完全禁带的大小，带隙率的物理意义为带隙的频宽与带隙中心频率的比值。第1条禁带对应的半径范围最大，为0．1a～0．4a，在R=0．18a处有最大带宽，带宽约为0．132 (ωa·(2πc)-1)，中心频率为0．384(ωa·(2πc)-1)，带隙率为34．375%。第2条禁带对应半径范围为0．22a～0．43a，该禁带在R=0．31a时有最大带宽，带宽为0．099(ωa·(2πc)-1)，中心频率为0．474 5 (ωa·(2πc)-1)，带隙率为20．86%。当圆柱的半径继续增加时，后两条禁带相继出现，当半径范围在0．34a～0．4a时，4条禁带同时存在。通过上面分析，可以看到，这种结构的光子晶体不存在TE禁带，这是因为圆柱间没有可以容纳D场线的连续通路，为使D场线满足连续条件，他们被迫穿过空气区，从而导致无法形成TE禁带。

2.1.2 介质圆柱折射率对禁带的影响

设定圆柱半径的初始值为0.35a，晶格周期为a，折射率步长取0．05，图2b为介质圆柱折射率对禁带的影响。可以看出，相对于TM模，TE模式的禁带频率较高，带宽较窄，笔者主要研究TM模的特性。TM模式主要存在4条禁带，每条禁带均呈柳叶形分布，当圆柱折射率增大时，中心频率低频化，禁带带宽与带隙率均呈增大趋势。当圆柱折射率为2.05时出现第1条禁带，这条禁带带宽较窄，对应最大带宽为0.04(ωa·(2πc)-1)，中心频率为0．227 5(ωa·(2πc)-1)，带隙率为17．58%。圆柱折射率取值2．15时，出现第2条禁带，对应最大带宽为0．07(ωa·(2πc)-1)，中心频率为0．387 7 (ωa·(2πc)-1)，带隙率为18．06%。圆柱折射率取值2．55时，出现第3条禁带，对应最大带宽为0．067 6(ωa·(2πc)-1)，中心频率为0．571 71(ωa·(2πc)-1)，带隙率为11．82%。通过分析数据可以得到以下结论:增加圆柱折射率是扩大禁带带宽、提高带隙率的有效手段之一，在设计时应该尽可能选用折射率较大的材料。

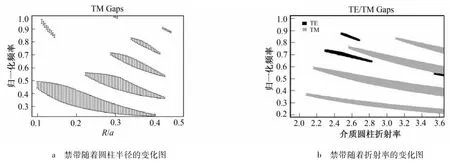
图2 禁带随正方排列介质圆柱半径和折射率的变化Fig.2 Effect of the radius and refractive index of square lattice dielectric cylinders on band gap

2．2 二维正方排列介质圆柱复式结构的禁带分析

2．2．1 介质圆柱半径对禁带的影响

利用软件进行仿真，对相关参数进行初始化设置，其中晶格周期为a，介质圆柱的介电常数为11．4，使其置于空气环境中，取半径步长为0．01a，图3a为该结构下禁带随半径变化的规律图。

从图3a可以看到，代表TM禁带的浅色部分面积很大，处于主导地位。该结构下TM禁带存在的半径范围非常大，在仿真中所设的半径起止范围内这条禁带始终存在。当半径逐渐增大时，该禁带的中心频率逐渐低频化，带宽先增大后减小，呈枣核形分布。当半径为0.27a时，带宽取得最大值为0．1 (ωa·(2πc)-1)，对应中心频率为0．28(ωa·(2πc)-1)，带隙率为38．4%。半径处于0．33a～0．5a范围内存在一条带宽较窄的TE禁带，当半径为0．45a时，其带宽最大值约为0．018 5(ωa·(2πc)-1)，中心频率为0．25(ωa·(2πc)-1)，带隙率为7．4%。不同于正方排列介质圆柱结构，该结构的TM禁带带宽和且半径范围较大，同时出现了TE禁带，虽然带宽较窄，但为产生完全禁带提供了可能。

2.2.2 介质柱折射率对禁带的影响

保持晶格周期不变，设置圆柱半径值为0.5a，折射率步长为0．1，此时介质柱折射率对禁带的影响如图3b所示。当介质柱折射率逐渐增大时，TM和TE禁带的中心频率均出现低频化趋势。

图3 复式结构圆柱半径和折射率对禁带的影响Fig.3 Effect of the radius and refractive index of cylinders of themultiple structure on band gap

对于TM禁带，带宽在折射率小于2.5的范围内逐渐增大，折射率增大到2.5后禁带带宽趋于平稳，为0.013(ωa·(2πc)-1)，带隙率随介质柱折射率的增大始终增大。在此结构下共出现两条TE禁带，第1条带宽在折射率小于3.5的范围内逐渐增大，大于3.5逐渐减小。对于第2条TE禁带，带宽在折射率小于4的范围内逐渐增大，当折射率达到4时，带宽趋于平稳，带隙率不断增大。从图3b可以看到，该结构在折射率为3.67～4.6范围内出现了完全禁带，随着折射率增大，中心频率向低频移动，带宽先增大后减小，当折射率为4.1时，有最大值0.01(ωa·(2πc)-1)，中心频率为0．150 5(ωa·(2πc)-1)，带隙率为6．64%。

该复式结构不但出现了TE禁带，并且产生了完全禁带(尽管带宽较窄)。通过以上分析可知:使用折射率大的材料易于获得完全禁带。

2.3 二维三角排列介质圆柱结构的禁带分析2.3.1 介质圆柱半径对禁带的影响

图1c为二维三角排列介质圆柱结构，设定晶格周期为a，介质圆柱的折射率为3．24，取半径步长为0．01a，光子晶体置于空气中，图4a为该结构下禁带随半径变化的规律图。可以看到，代表TM禁带的浅色部分处主导地位，其中心频率均随介质圆柱半径的增加而降低，禁带带宽先增大后减小，呈枣核形分布。在低频区主要存在两条禁带。第1条处于半径在0．06a～0．43a的范围内，当半径为0．149a时，具有带宽最大值为0．188(ωa·(2πc)-1)，对应中心频率为0．439(ωa·(2πc)-1)，带隙率为42．82%。第2条处于半径在0．21a～0．44a的范围内，当半径为0．29a时，具有带宽最大值为0．123(ωa·(2πc)-1)，对应中心频率为0．51(ωa·(2πc)-1)，带隙率为24．12%。可以看出，相比于正方排列介质圆柱结构，三角排列介质圆柱结构每条TM模的最大禁带带宽都有所增加，带隙率也相应增大。

2.3.2 介质柱折射率对禁带的影响

设定晶格周期为a，取折射率步长为0．05，当取定圆柱半径为0．29a时，禁带随介质圆柱折射率变化趋势如图4b所示。该结构主要有3条TM禁带。禁带中心频率随着折射率的增加而降低，带宽与带隙率均增大。第1条禁带在折射率为3.24时，带宽达到0.096 8(ωa·(2πc)-1)，对应中心频率为0．291 3 (ωa·(2πc)-1)，带隙率为33．23%。第2条禁带在折射率为3．24时，带宽为0．123 7，对应中心频率为0．5(ωa·(2πc)-1)，带隙率为24．74%。第3条禁带在折射率为3．24时，带宽为0．1(ωa·(2πc)-1)，对应中心频率为0．739(ωa·(2πc)-1)，带隙率为13．53%。该结构下光子晶体不存在TE禁带。通过以上分析可知:为提高禁带带宽和带隙率，应该选用高折射率材料。

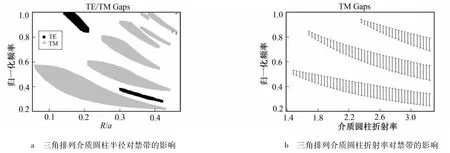
图4 三角排列介质圆柱半径和折射率对禁带的影响Fig.4 Effect of the radius and refractive index of triangular lattice dielectric cylinders on band gap

2.4 二维蜂窝圆柱结构的禁带分析

对三角排列介质圆柱结构加以改变，所得即为图1d所示的新结构，这种结构由多个六边形紧密排列形成，形状似蜜蜂窝，故称之为蜂窝结构。

2.4.1 介质圆柱半径对禁带的影响

设定晶格周期为a，介质圆柱介电常数为11．4，取半径步长为0．01a，光子晶体置于空气中，图5a为该结构下介质圆柱半径的变化对禁带的影响。可以看到，该结构下主要存在两条完全禁带。其中在半径为0．19a～0．35a的范围内存在较大的完全禁带，禁带中心频率随着半径的增大而降低，带宽先增大后减小，呈枣核形分布，其最大带宽为0．052 2(ωa·(2πc)-1)，当半径为0．25a时，对应中心频率为0．554 8(ωa·(2πc)-1)，带隙率为9．4%。第2条完全禁带在半径为0．274a～0．425a范围内存在。分布特点与第一条相似，当半径达到0．35a时，具有最大带宽为0．023 6(ωa·(2πc)-1)，对应中心频率为0．383 4(ωa·(2πc)-1)，带隙率为6．155%。

2．4．2 介质柱折射率对禁带的影响

通过分析可看出:禁带中心频率随着圆柱折射率的增大而降低，带宽和带隙率随之增大。介质柱折射率对蜂窝结构光子晶体影响如图5b所示，设定晶格周期为a，圆柱半径为0．25a，光子晶体置于空气环境中。通过图5b可知，该结构下折射率对禁带的影响与之前的结论存在差异。该结构下主要存在两条完全禁带。其中第1条存在于折射率为4.05～5的范围内，该完全禁带中心频率随着折射率的增大而降低，带宽与带隙率逐渐增加。第2条较大的完全禁带存在于折射率为2.9～5的范围内，其禁带中心频率随折射率的变化趋势与第1条完全禁带类似，但带宽先增大后减小，呈枣核形分布，当折射率为3.4时，最大带宽为0.055(ωa·(2πc)-1)，对应中心频率为0．554 2(ωa·(2πc)-1)，带隙率为9．92%。

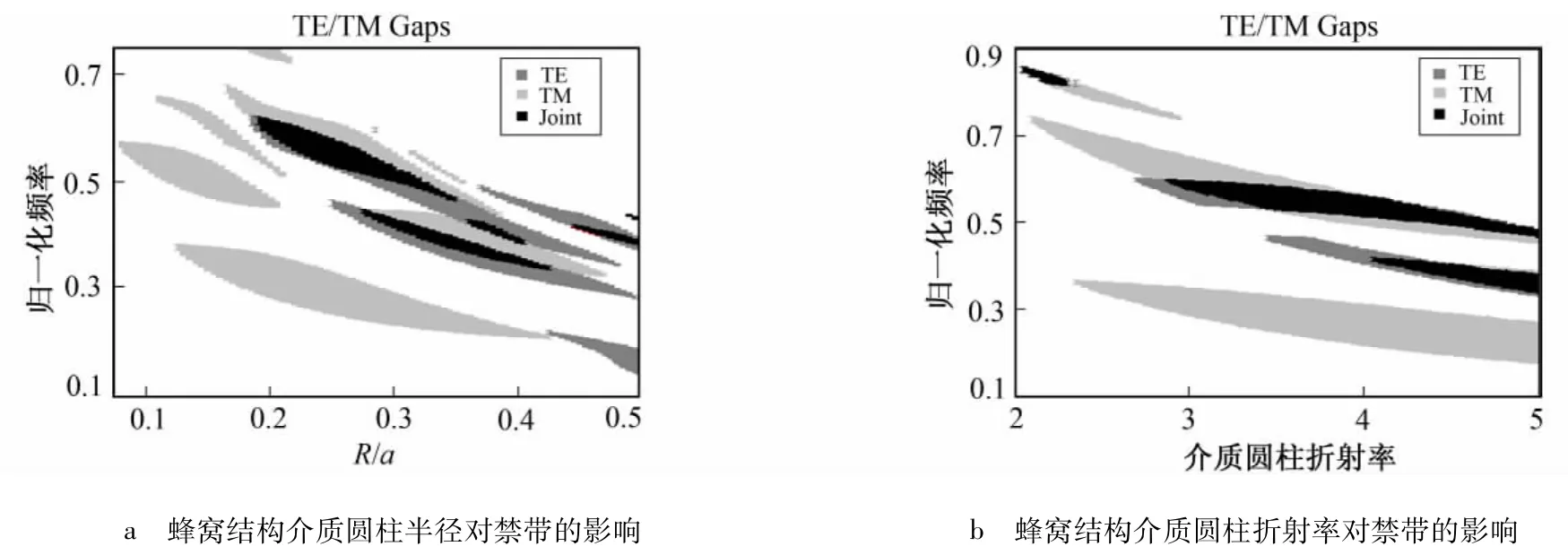
图5 蜂窝结构介质圆柱半径和折射率对禁带的影响Fig.5 Effect of the radius and refractive index of honeycomb dielectric cylinders on band gap

3 几种结构禁带的比较

对于介质柱结构，降低禁带中心频率的方法有两种:增大介质圆柱半径和增加介质柱折射率。正方排列介质圆柱只存在TM禁带，而其复式结构可同时产生TM禁带和TE禁带，但TE禁带带宽较窄。当介质圆柱半径为0.5a、折射率大于3.67时，存在一条完全禁带，对应带隙率为6.64%。与正方排列结构相比，三角排列介质圆柱结构的TM禁带带宽与带隙率均有所增大。蜂窝结构产生了多条TE禁带，其形成的两条完全禁带具有较大带宽，当介质圆柱半径为0.25a、介质圆柱折射率为3.4时，其中完全禁带有最大带隙率9.92%。

4 结 语

对于介质柱结构，降低禁带中心频率的方法有两种:增大介质圆柱半径和增加介质柱折射率。采用复式介质圆柱结构可以有效增加TM禁带的带宽，并有利于形成TE禁带和完全禁带。对于正方排列介质圆柱复式结构，当介质圆柱半径为0.5a、介质圆柱折射率大于3．67时，存在一条带隙率为6．64%左右的完全禁带;对于蜂窝结构，当介质圆柱半径为0．25a、介质圆柱折射率为3.4时，其完全禁带有最大带隙率9.92%。由此可见，改变晶胞结构，降低结构对称性是寻求完全禁带的一种可行方法。

［1］YABLONOVITCH E.Inhibited Spontaneous Emission in Solid-State Physics and Electronics［J］.Phys Rev Lett，1987，58(20):2059-2061.

［2］JOHN S.Strong Localization of Photons in Certain Disordered Dielectric Super-Lattice［J］.Phys Rev Lett，1987，58(23): 2486-2489.

［3］王媛媛，何晓东，胡贵军，等.一维光子晶体微谐振腔的调谐特性与品质因子 ［J］.光子学报，2009，38(2):285-288. WANG Yuanyuan，HE Xiaodong，HU Guijun，et al.Tuning Characteristics and Quality Factor of One-Dimension Photonic Crystal Micro-Cavity［J］.Acta Photonica Sinica，2009，38(2):285-288.

［4］吴冰冰，何晓东，薛伟，等.一维非线性光子晶体全光开关的数值研究［J］.光子学报，2009，38(2):293-297. WU Bingbing，HE Xiaodong，XUEWei，et al.Numerical Research on One Dimension Nonlinear Photonic Crystal All-Optical Switching［J］.Acta Photonica Sinica，2009，38(2):293-297.

［5］黄韩娟，欧阳征标，许桂雯，等.复周期光子晶体的理想多通道滤波特性［J］.光电子·激光，2003，14(1):50-53. HUANG Hanjuan，OUYANG Zhengbiao，XU Guiwen，et al.Investigation of Perfect Multichannel Filtering Properties of Complex Period Photonic Crystals［J］.Journal of Optoelectronics·Lasers，2003，14(1):50-53.

［6］PENDRY JB.Calculating Photonic Band Structure［J］.Phys Condon Matter，1996(8):1086-1108.

［7］MARADUDIN A A，MCGURN A R.Photonic Band Structure of a Truncated，Two-Dimensional，Periodic Dielectric Medium［J］.Opt Soc Am，1993，10(2):307-313.

［8］HO K M，CHAN C T，SOUKOULIS.Existence of a Photonic Gap in Periodic Dielectric Structure［J］.Phys Rev Lett，1990，75(12):1676-1678.

［9］陆晓东，韩培德，全宇军，等.格点形状和取向对二维光子晶体禁带的影响［J］.光电子·激光，2005，16(11): 1336-1341. LU Xiaodong，HAN Peide，QUAN Yujun，etal.Effects of Shapes and Orientations of Rods on the Photonic Band Gap in Two Dimensional Photonic Crystals［J］.Journal of Optoelectronics Laser，2005，16(11):1336-1341.

［10］PARK J HWANG，Y LEE，KIM J.Square-Lattice Photonic Band-Gap Single-Cell Laser Operating in the Lowest-Order Whispering Gallery Mode［J］.Appl Phys Lett，2002，80(21):3883-3885.

［11］方云团，余士林.一维随机光子晶体中的光子局域化［J］.激光与红外，2004，34(2):137-139. FANG Yuntuan，XU Shilin.Phenomena of Photonic Localization form Two Dimension Random Photonic Crystal［J］.Laser＆Infrared，2004，34(2):137-139.

［12］梁华秋，冯尚申.在高频区存在巨带隙的长方晶格二维光子晶体［J］.光子学报，2005，34(5):781-784. LIANG Huaqiu，FENG Shangshen.Giant Band Gaps of Rectangle Lattice 2D Photonic Crystal at High Frequency［J］. Acta Photonica Sinica，2005，34(5):781-784.

［13］房淑芬，李集思，苏适，等.一维光子晶体的禁带特性［J］.吉林大学学报:理学版，2009，47(1):98-101. FANG Shufen，LI Jisi，SU Shi，et al.Band Gap Properties of1-D Photonic Crystal［J］.Journal of Jilin University:Science Edition，2009，47(1):98-101.

［14］RAGINISRIVASTAVA，THAPA K B，SHYAM PATI，et al.Negative Refraction in 1-D Photonic Crystals［J］.Solid State Communications，2008，147(3/4):157-160.

［15］王媛媛.光子晶体微谐振腔的特性研究［D］.长春:吉林大学通信工程学院，2009. WANG Yuanyuan.Performance Research of Photonic Crystal Micro-Cavity［D］.Changchun:College of Communication Engineering，Jilin University，2009.

［16］王媛媛，宋健，黄益强，等.二维正方柱结构光子晶体禁带的研究［J］.激光与红外，2009，39(9):969-973. WANG Yuanyuan，SONG Jian，HUANG Yiqiang，et al.Research of Band Gap of Two-Dimensional Photonic Crystal with Square Rods［J］.Laser＆Infraed，2009，39(9):969-973.

［17］李爱萍，王安全，纪延俊.大带隙2维正方晶格光子晶体的优化设计［J］.激光技术，2012，36(4):508-511. LIAiping，WANG Anquan，JI Yanjun.Optimal Design of 2-D Columnar Photonic Crystal with Square Lattice and Large Bandgap［J］.Laser Technology，2012，36(4):508-511.

(责任编辑:张洁)

Research of Band Gap in Compound Two-Dimensional Photonic Crystal Based on Dielectric Cylinder Structure

WANG Yuanyuan1，ZHANG Lixin2，WANG Yiyang3，YAN Zhiyu3，HE Xiaodong3

(1.College of Medical Informatics，Hainan Medical University，Haikou 571199，China; 2.Department of Management，Jilin Provincial Radiation Environmental Supervision Station，Changchun 130012，China; 3.College of Communication Engineering，Jilin University，Changchun130012，China)

In order to quest for large band gap or complete band gap of two-dimensional photonic crystal，the band gap of the structure in two-dimensional square lattice and triangular latticewith dielectric cylinder using the plane wavemethod，and the band gap of the compound structure by changing the unite cell are studied.Results show that to the dielectric rod，themiddle frequencies of the band gap will reducewith the increase of the radius and refractive index of the dielectric rod.The compound dielectric cylinder structure has big TM(Transverse Magnetic)band gap，and itmakes TE(Transverse Electric)band gap and the formation of thismake complete band gap be possible.Changing the unite cell to reduce the symmetry of the structure is a feasible method to quest for complete band gap.

photonic crystal;two-dimensional photonic crystal;plane wave method;band gap;complete band gap

TN248

A

1671-5896(2015)06-0668-07

2015-04-16

长春市国际合作科技计划基金资助项目(2009GH12)

王媛媛(1984— )，女，海口人，海南医学院讲师，主要从事材料的设计及性能研究，(Tel)86-13136011039(E-mail) 232919859@qq.com;通讯作者:何晓东(1963— )，女，长春人，吉林大学教授，硕士生导师，主要从事全光通信网的关键技术和器件、光子晶体及器件研究，(Tel)86-13069003226(E-mail)hexiaodong220@163.com。