宽绝对禁带的一维磁性光子晶体结构∗

陈敏 万婷 王征 罗朝明 刘靖

(湖南理工学院信息与通信工程学院,复杂工业物流系统智能控制与优化湖南省重点实验室,岳阳 414006)(2016年4月22日收到;2016年10月16日收到修改稿)

宽绝对禁带的一维磁性光子晶体结构∗

陈敏 万婷 王征 罗朝明†刘靖

(湖南理工学院信息与通信工程学院,复杂工业物流系统智能控制与优化湖南省重点实验室,岳阳 414006)(2016年4月22日收到;2016年10月16日收到修改稿)

提出了一种具有宽绝对禁带的一维磁性光子晶体结构,该结构由相同的折射率和物理厚度以及不同的波阻抗的两种磁性材料交替组合而成.通过传输矩阵法分析可得,相比于非磁性光子晶体,该光子晶体的禁带对入射角和偏振都不敏感,从而具有更宽的绝对禁带.合适地调节两种磁性材料的参数,增加两者波阻抗的差值,该光子晶体的绝对禁带宽度也相应地增加;调节两种磁性材料的物理厚度,其绝对禁带中心也会随之调整;最后,将两个满足上述条件的一维磁性光子晶体组成异质结构,其第一禁带宽度与禁带中心之间的比值可达到1.41以上.

绝对禁带,光子晶体,磁性材料

1引 言

近年来,光子晶体的许多优良特性和潜在应用不断被发现,其研究已经引起越来越多的研究者的关注[1,2].光子晶体又称“光学半导体”,它具有的最为显著的性质是光子禁带[3,4].光子晶体能够阻止频率落在光子禁带中的电磁波的传播,但是通常情况下光子禁带对入射角和偏振态都较为敏感.为了实现某一频带的电磁波在任意偏振和角度入射下都能被阻止,可以通过合理设计光子晶体结构使得其具有绝对禁带[5−8].这种绝对禁带在全方位高反射镜[9,10]、低损耗波导[11]、光开关[12]和空间滤波器等[13−15]方面都具有许多潜在的应用.

非磁性光子晶体的绝对禁带通常是比较窄的,有必要对其禁带进行扩展.目前扩展光子晶体禁带的方法主要有三种,第一种是通过调整光子晶体的材料和旋转对称性来扩展禁带[8,16];第二种是将几个光子晶体组成异质结构来扩展禁带[17−20].但是前面两种方法对非磁性光子晶体的禁带扩展都是在某一种偏振下进行的,同时该禁带还对入射角较为敏感,从而绝对禁带扩展比较小.随着超常介质材料的出现,人们提出了第三种扩展禁带的方法,通过将超常介质材料引入到光子晶体中来扩展禁带[21−23].由于超常介质材料具有对入射角和偏振的不敏感性,从而能够扩宽光子的绝对禁带,但这种超常介质材料在自然界中是不存在的且其制备相当困难.为了解决这一不足,Ouyang等[24]将磁性材料引入光子晶体中,使得其绝对禁带得到了一定的扩展.

本文提出了一种宽绝对禁带的一维磁性光子晶体结构,组成该结构的两种磁性材料具有相同的折射率和物理厚度以及不同的波阻抗.该结构禁带对光的入射角和偏振态都具有不敏感性.通过改变该结构的波阻抗、材料的物理厚度以及构成的异质结构来研究其对光子禁带的影响.

2结构模型与理论

图1(a)是由两种磁性材料构成的一维磁性光子晶体结构(AB)N示意图,组成光子晶体的A,B两种材料的折射率和磁导率分别为:nA,µA,nB,µB,对应的物理厚度分别为dA,dB,N表示周期数.设平面电磁波由空气入射到光子晶体中,θ为其入射角.为了准确地描述这种结构的传输特性,需要确定任意波矢分量的反射和透射,该结构可由下面的2×2矩阵来表示[25,26]:

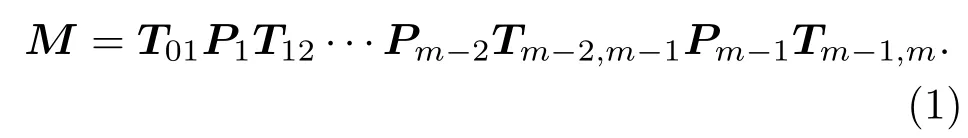
这里的Tm−1,m为第m−1层到第m层的转换矩阵,

其中rm−1,m和tm−1,m则分别表示从第m−1层到第m层的反射系数和透射系数;Pm为第m层的传输矩阵

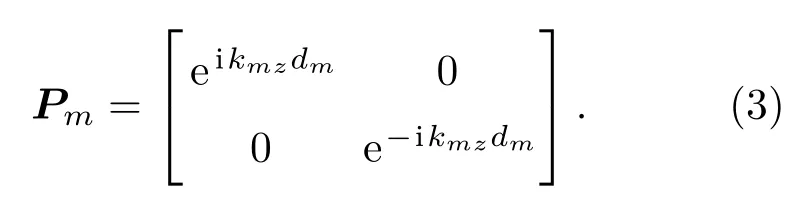
上式中的dm和kmz分别表示第m层介质的厚度和沿z方向的波矢分量.在本文的讨论中,rAB,tAB分别表示图1(b)所示的介质A到介质B界面的反射系数和透射系数;rBA,tBA则分别表示图1(c)所示的介质B到介质A界面的反射系数和透射系数.具体表示为[25,26]

上述公式中θA和θB分别是入射电磁波在介质A和介质B中的传输角,表示介质A对应的波阻抗,ηB则表示介质B对应的波阻抗.整个光子晶体的透射系数和反射系数可由下面的公式来描述[25]:

图1 (网刊彩色)光子晶体结构示意图及两个不同界面的传输图Fig.1.(color online)Schematic of photonic crystal structure and two transmission diagrams of di ff erent interfaces.

其中字母p,s分别对应平行和垂直偏振情形.整个介质的反射率和透射率用下式来表示[25]:上式中kmz,θm和k0z,θ0分别表示出射介质m和入射介质中沿z方向的波矢分量和传输角.

根据(1)式,图1(a)所给出的一维光子晶体结构可用下面的矩阵来表示:

M=T0A(PATABPBTBA)N−1PATABPBTB0.(10)为了获得绝对禁带,必须考虑其偏振特性,只有当禁带对偏振不敏感时才能获得更宽的绝对禁带.由(1)—(9)式可知,物理厚度相同的各层对应相同的传输矩阵Pm,因而Pm是与偏振无关的;而转换矩阵Tm,m−1由于rm−1,m和tm−1,m的偏振敏感性而偏振相关.在图1结构中,很明显影响该结构偏振特性的是介面A到界面B的反射系数rAB和透射系数tAB,以及界面B到界面A的反射系数rBA和透射系数tBA.结合(4)—(7)式分析可知,只有当θA和θB相等时(即组成光子晶体结构的两种材料的折射率相等时),不同偏振对应的透射系数和反射系数才相等,从而使得TE和TM是偏振不敏感的,以达到扩展光子晶体绝对禁带的目的.因此,我们可得出满足下面条件的磁性光子晶体结构能扩展其绝对禁带宽度,即组成光子晶体结构的两种材料具有相同的折射率和物理厚度以及不同的波阻抗.

3数值模拟与分析

首先,我们比较研究一维磁性和非磁性光子晶体两种结构的禁带特性.为了研究的方便,我们参照文献[24,27,28]忽略材料损耗来选取相关参数,理论探索一维磁性光子晶体的禁带特性.根据第二部分得出的扩展禁带的条件(相同的折射率和物理厚度以及不同的波阻抗),我们选取的两种磁性材料A和B的结构参数如下:折射率nA=nB=n=3.4;磁导率µA=2.5,µB=1.5;每层介质的物理厚度为dA=dB=λ0/(4n),其中λ0为真空中禁带的中心波长;周期数N=6.通过采用传输矩阵法[13−15],得到了在不同偏振情况下以不同角度入射的一维磁性光子晶体(AB)6的传输谱,如图2(a)—(d)所示.从该图中可以看出,在禁带处TE和TM偏振的传输曲线几乎重合,从而可认为该禁带是偏振不敏感的;而且禁带出现的位置几乎不随角度的改变而移动,这些都有利于绝对禁带的扩展,该结构绝对禁带的归一化频率带宽(禁带宽度与禁带中心之间的比值)达到了0.41.为了与之进行对比,我们选取了具有相同波阻抗比值的两种非磁性材料C和D(即ηA/ηB= ηC/ηD=5/3),其结构参数为nC=1.5,nD=2.5,dC= λ0/(4nC),dD= λ0/(4nD),该非磁性光子晶体 (CD)6的传输谱如图2(a′)—(d′)所示.从该图中可以看出,非磁性光子晶体的TE和TM偏振的传输曲线随着入射角的增加差别越来越大,从而该禁带是偏振相关的;并且随着角度的增加TE偏振的禁带左右边缘都向右移动,但TM偏振的禁带左边缘向右移动而右边缘先向右移后又向左偏移;其绝对禁带的归一化频率带宽只有0.14,相比于前面的磁性光子晶体而言,其绝对禁带宽度明显窄得多.

图2 (网刊彩色)一维磁性光子晶体和非磁性光子晶体的传输谱Fig.2.(color online)Transmission spectrum of one dimensional magnetic photonic crystals and non-magnetic photonic crystals.

需要指出的是,通常情况下的磁性材料都是有损耗的,下面研究损耗对本文中磁性光子晶体禁带特性的影响.众所周知,损耗参数可用折射率的虚部来描述[29,30],在这里将磁性材料A和B的折射率调整为:nA=nB=3.4+0.1i,其他参数与图2(a)—(d)保持一致,相应的含损耗磁性材料的一维光子晶体(AB)6的传输谱如图3(a)—(d)所示.由图中可看出其透过率相对于图2(a)—(d)中不考虑损耗时的情形略有降低,但绝对禁带宽度变化很小,几乎不变.因此在本文的讨论中,为了研究的方便,都忽略了磁性材料的损耗参数对禁带特性的影响,即假定磁性材料是没有损耗的.

根据一维磁性光子晶体绝对禁带扩展的条件,将进一步研究两种材料的波阻抗对其绝对禁带宽度的影响.假定折射率和物理厚度都与前面的分析一致,即nA=nB=n=3.4,dA=dB=λ0/(4n).在保持两种材料介电常数不变的情况下调节磁导率使得波阻抗之间的差值依次增大,图4(a)—(c)分别是两种磁性材料比值为ηA/ηB=2,4,6的光子晶体结构(AB)6的禁带.从图中可以得出,ηA/ηB=2,4,6对应的绝对禁带的归一化频率范围分别为0.78—1.25,0.6—1.44,0.50—1.53,其归一化的频率带宽分别为0.47,0.84,1.03.由此可以总结出,随着两种材料波阻抗差值的增加,该光子晶体结构的绝对禁带的频率带宽得到了显著的扩宽.

然后,将研究探讨每层材料的物理厚度对该光子晶体结构传输特性的影响.我们选取了图4(b)中除每层物理厚度外相同的其他结构参数,即折射率nA=nB=n=3.4,波阻抗比值为ηA/ηB=4,磁导率µA=6.0,µB=1.5;同时将每层物理厚度分别调整为dA=dB=λ0/(8n)和dA=dB=λ0/(16n),其对应的不同角度下的传输谱如图5(a)—(d) 和图5(a′)—(d′)所示. 对比两者可以发现,当材料的物理厚度变小时,禁带中心依次向右移动,其归一化频率带宽分别为0.78和0.80.由此我们可以总结得出,随着材料每层的物理厚度d的缩小,绝对禁带的禁带中心依次右移,而对禁带的归一化频率带宽的影响很小.

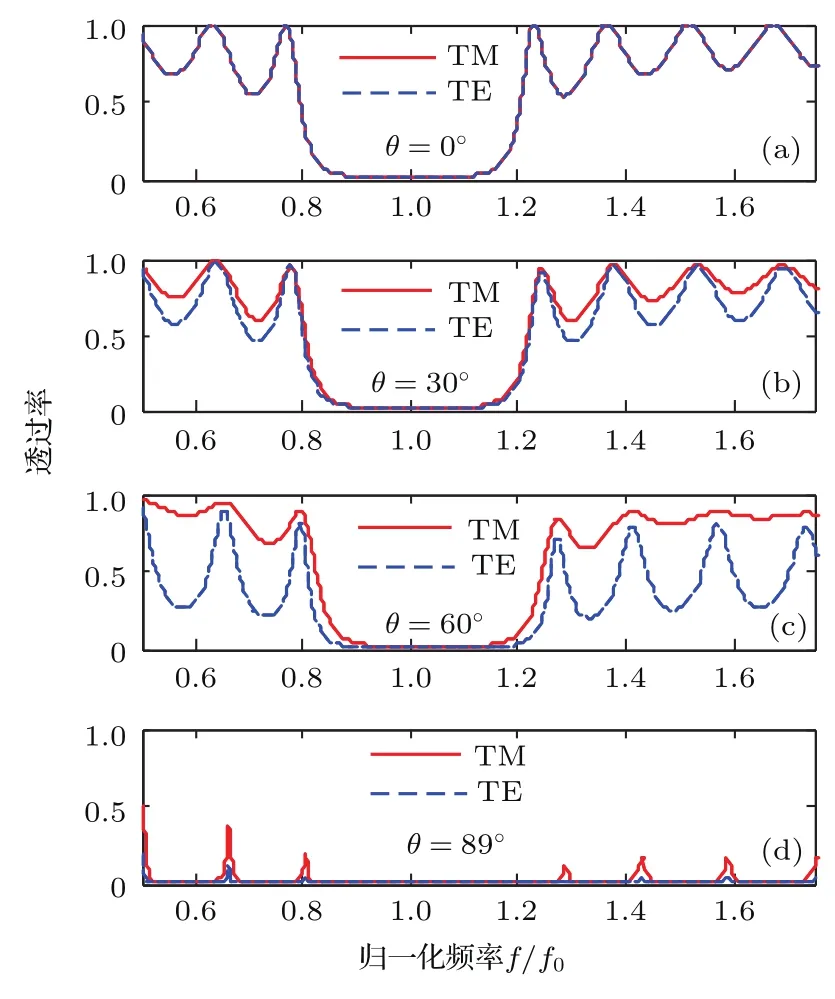
图3 (网刊彩色)含损耗磁性材料一维光子晶体的传输谱Fig.3.(color online)Transmission spectrum of one dimensional magnetic photonic crystals containing the lossy magnetic materials.

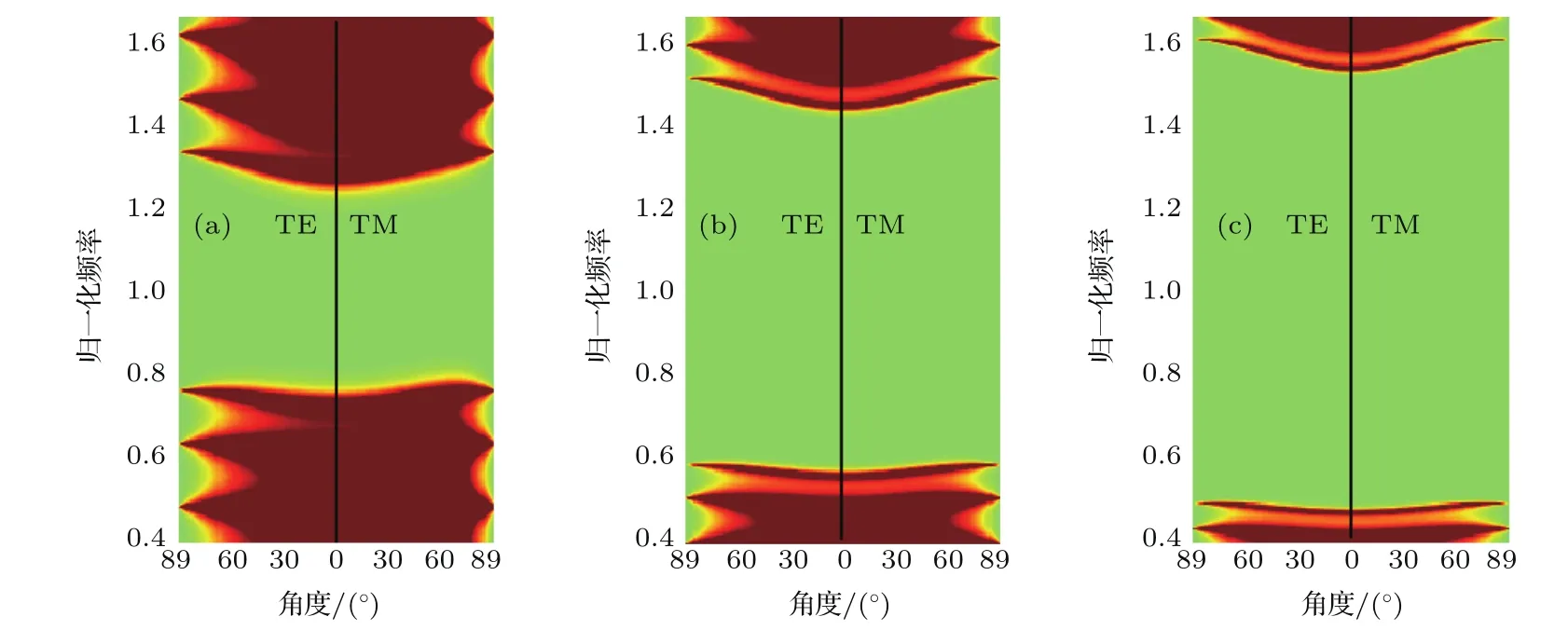
图4 (网刊彩色)不同波阻抗比的一维磁性光子晶体禁带结构Fig.4.(color online)Bandgap structures of one-dimensional magnetic photonic crystals with di ff erent wave impedances.

图5 (网刊彩色)不同厚度的一维磁性光子晶体传输谱Fig.5.(color online)Transmission spectra of one-dimensional magnetic photonic crystals with di ff erent thicknesses.

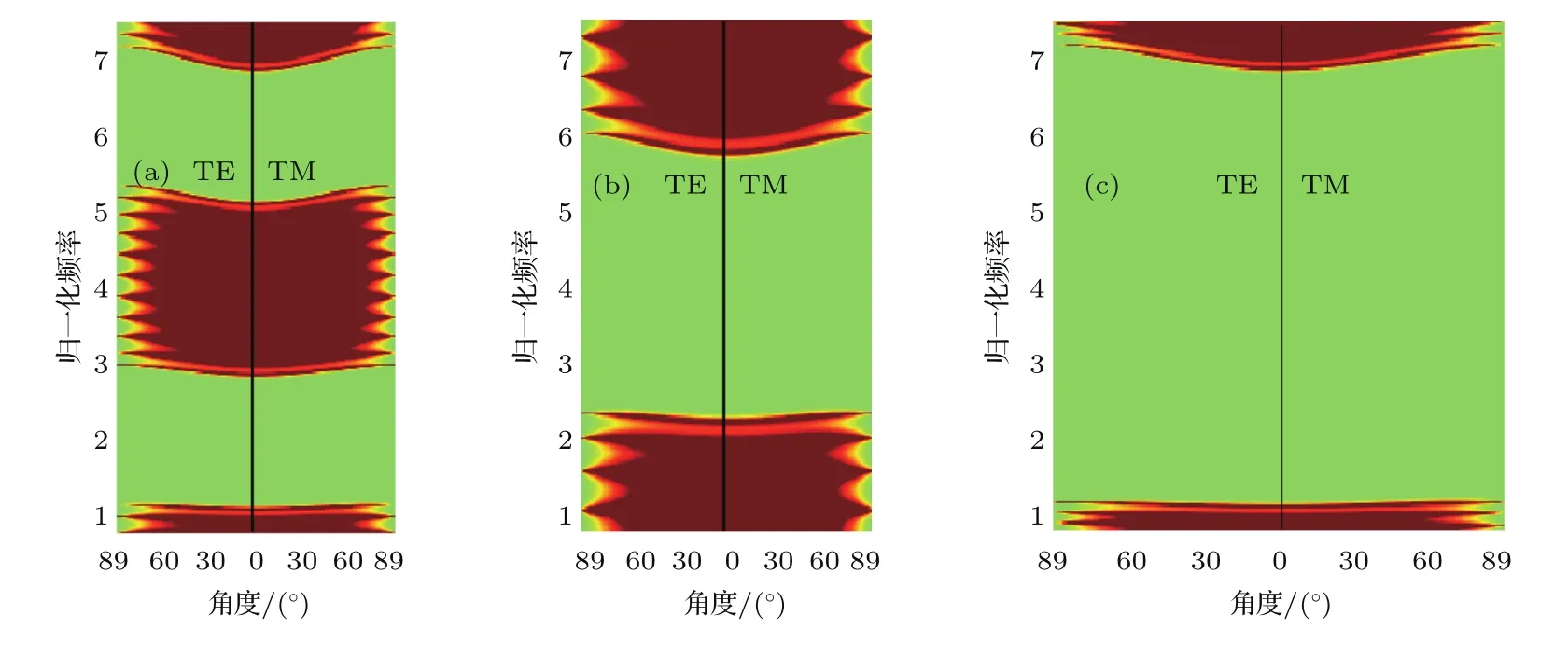
图6 (网刊彩色)三种不同结构的光子晶体的禁带结构Fig.6.(color online)Bandgap structures of three kinds of photonic crystals with di ff erent structures.

最后研究利用该一维磁性光子晶体组成的异质结构来进一步扩展其绝对禁带.异质结构的绝对禁带的扩展应满足叠加原理,即要求组合成异质结构的两个光子晶体结构中的一个结构所产生的导带被包含在另一个结构的绝对禁带中.由此,我们选择了图5中的两个磁性光子晶体,并重画了它们的禁带结构图,即每层材料的物理厚度为dA=dB= λ0/(8n)和dA′=dB′= λ0/(16n)时的光子晶体的禁带结构图,具体如图6(a)—(b)所示.从图6(a)中可以看出,第一个光子晶体结构(AB)6的第一和第二绝对禁带的归一化频率范围依次为 1.18—2.85和5.37—6.85;图6(b)为第二个光子晶体结构(A′B′)6的禁带结构,其绝对禁带的归一化频率范围为2.37—5.68.很明显,第一个光子晶体的第一和第二绝对禁带之间的导带被包含在第二个光子晶体的绝对禁带中,从而有利于禁带的扩展.图6(c)为这两个光子晶体组成的异质结构(AB)6(A′B′)6的禁带结构,其绝对禁带的归一化频率范围为1.18—6.85,对应的归一化频率带宽达1.41.结合图6(a)—(c)可以总结出,满足上述叠加条件的两个光子晶体结构所构成的异质结构的绝对禁带就是这两个光子晶体绝对禁带的叠加,从而实现了绝对禁带的扩展.

4结 论

本文提出了一种具有宽绝对禁带的一维磁性光子晶体结构,该结构由折射率相同和物理厚度相同但波阻抗不同的两种磁性材料分别交替组合而成.首先,我们对比分析了磁性和非磁性一维光子晶体的禁带特性,进一步论证了上述绝对禁带扩展的条件.然后研究了波阻抗的改变对该绝对禁带扩展的影响,结果发现:随着两种材料波阻抗差值的增大,绝对禁带得到了很明显的扩展.同时也得出了在保持所有波阻抗不变的情况下,通过磁性材料的物理厚度的调整,其禁带中心随之改变,但绝对禁带宽度几乎不变.最后我们用两个一维磁性光子晶体构成异质结构,研究发现该异质结构的绝对禁带宽度是这两个光子晶体绝对禁带的叠加.这种磁性光子晶体具有宽的绝对禁带,在集成光学、光纤通信以及激光系统等领域有着潜在的应用,比如可实现具有偏振无关、全方向等良好性能的反射镜、光开关、光学滤波器等.

[1]Yablonovitch E 1987 Phys.Rev.Lett.58 2059

[2]John S 1987 Phys.Rev.Lett.58 2486

[3]Joannopoulos J D,Meade R D,Winn J N 1995 Photonic Crystals:Molding the Flow of Light(Princeton:Princeton Univ.Press)

[4]Sakoda K 2001 Optical Properties of Photonic Crystals(Berlin:Springer-Verlag)

[5]Dowling J P 1998 Science 282 1841

[6]Liu H,Yao J Q,Li E B,Wen W Q,Zhang Q,Wang P 2006 Acta Phys.Sin.55 230(in Chinese)[刘欢,姚建铨,李恩邦,温午麒,张强,王鹏2006物理学报55 230]

[7]Cheng X P,Cao Q X 2008 Acta Phys.Sin.57 3249(in Chinese)[程旭攀,曹全喜 2008物理学报 57 3249]

[8]Fink Y,Winn J N,Fan S,Chen C,Michel J,Joannopoulos J D,Thomas E L 1998 Science 282 1679

[9]Ibanescu M,Fink Y,Fan S,Thomas E L,Joannopoulos J D 2000 Science 289 415

[10]Jiang L,Zheng G,Shi L,Yuan J,Li X 2008 Opt.Commun.281 4882

[11]Hart S D,Maskaly G R,Temelkuran B,Prideaux P H,Joannopoulos J D,Fink Y 2002 Science 296 510

[12]Lu Y H,Huang M D,Park S Y,Kim P J,Nahm T U,Lee Y P,Rhee J Y 2007 J.Appl.Phys.101 036110

[13]Luo Z M,Tang Z,Xiang Y,Luo H,Wen S 2009 Appl.Phys.B 94 641

[14]Luo Z M,Qu S,Liu J,Tian P 2013 J.Mod.Opt.60 171

[15]Luo Z M,Chen M,Liu J,Lei D J 2016 Opt.Commun.365 120

[16]Winn J N,Fink Y,Fan S,Joannopoulos J D 1998 Opt.Lett.23 1573

[17]Zhang J,Benson T M 2013 J.Mod.Opt.60 1804

[18]Suthar B,Bhargava A 2012 Opt.Commun.285 1481

[19]Joseph S,Ha fi z A K 2014 Optik 125 2734

[20]Han P,Wang H 2005 J.Opt.Soc.Am.B 22 1571

[21]Feng X,Li H 2013 Eur.Phys.J.D 67 1

[22]Xiang Y,Dai X,Wen S,Fan D 2007 J.Opt.Soc.Am.A 24 A28

[23]Yin C P,Dong J W,Wang H Z 2009 Eur.Phys.J.B 67 221

[24]Ouyang Z B,Mao D,Liu C P,Wang J C 2008 J.Opt.Soc.Am.B 25 297

[25]Yariv A,Yeh P 2007 Optical Electronics in Modern Communications(New York:Oxford University Press)pp199–204

[26]Yeh P 1988 Optical Waves in Layered Media(New York:Wiley)pp58–67

[27]Sigalas M M,Soukoulis C M,Biswas R,Ho K M 1997 Phys.Rev.B 56 959

[28]Teng C C,Zhou W,Zhuang Y Y,Chen H M 2016 Acta Phys.Sin.65 024210(in Chinese)[滕晨晨,周雯,庄煜阳,陈鹤鸣2016物理学报65 024210]

[29]Kong J A(translated by Wu J)2003 Electromagnetic Wave Theory(Beijing:Publishing House of Electronics Industry)pp81,82(in Chinese)[孔金瓯著(吴季译)2003电磁波理论(北京:电子工业出版社)第81,82页]

[30]Wang L G,Chen H,Zhu S Y 2005 Opt.Lett.30 2936

PACS:42.70.Qs,42.55.Tv,75.50.–yDOI:10.7498/aps.66.014204

*Project supported by the National Natural Science Foundation of China(Grant No.61205126),the Science and Technology Program of Hunan Province,China(Grant No.2016TP1021),and the Experimental Project of College Students in Hunan Province and Hunan Institute of Science and Technology,China.

†Corresponding author.E-mail:zhaomingluo@hnu.edu.cn

One-dimensional magnetic photonic crystal structures with wide absolute bandgaps∗

Chen Min Wan Ting Wang Zheng Luo Zhao-Ming†Liu Jing

(Key Laboratory of Hunan Province on Intelligent Control and Optimization of Complex Industrial Logistics System,College of Information and Telecommunications Engineering,Hunan Institute of Science and Technology,Yueyang 414006,China)(Received 22 April 2016;revised manuscript received 16 October 2016)

The photonic absolute bandgaps have many potential applications in speci fi c fi elds,and some methods to enlarge the absolute bandgaps,such as adjusting the material and the rotational symmetry,constituting a heterostructure have been explored.Recently,with the occurring of metamaterial,the photonic crystal based on metamaterial has also realized the wide absolute bandgaps.However,the metamaterial is an arti fi cially structured material of which the construction is more complicated.In this paper,one-dimensional magnetic photonic crystal structure with wide absolute bandgaps is proposed,which is composed of two kinds of magnetic materials with the same refractive index and physical thickness but di ff erent wave impedances.First of all,the transmission properties of one-dimensional magnetic and non-magnetic photonic crystals with the same wave impedance ratio are studied by using transfer matrix method.It is shown that the normalized frequency bandwidth of magnetic photonic crystal,i.e.the ratio of the band of bandgap to its center,is 0.41,while the normalized frequency bandwidth of the non-magnetic photonic crystal is 0.14.From the results,we can conclude that the absolute bandgap of the above magnetic photonic crystal is wider than that of non-magnetic photonic crystal because the former bandgap is not sensitive to the incident angle nor polarization.Secondly,we adjust the wave impedance ratios of the two kinds of magnetic materials and make them respectively reach 2,4and 6,with the refractive index and the physical thickness kept unchanged.By analyzing their transmission properties,it is found that the normalized frequency bandwidths of the absolute bandgaps are respectively 0.47,0.84and 1.03,and the greater the di ff erence between the two wave impedances,the wider the normalized frequency bandwidth is.Thirdly,we investigate the in fl uence of the per-layer physical thickness of the magnetic material on the bandgap,with the other parameters remaining unchanged.It is shown that the center of the absolute bandgap shifts toward high frequency with the decrease of the per-layer physical thickness.Finally,a kind of heterostructure is constructed by the above two one-dimensional magnetic photonic crystals.The normalized frequency ranges of the fi rst and the second absolute bandgap of one magnetic photonic crystal structure are respectively 1.18–2.85and 5.37–6.85.The normalized frequency range of the absolute bandgap of the other magnetic photonic crystal is 2.37–5.68.The normalized frequency range of the absolute bandgap of the heterostructure can be enlarged to 1.18–6.85and the corresponding normalized frequency bandwidth can reach more than 1.41.The wide absolute bandgaps can be applied to integrated optics,optical fi ber communication and high-power laser systems,according to which we may design the polarization-independent and omnidirectional devices such as re fl ectors,optical switchers and optical fi lters.

absolute bandgap,photonic crystals,magnetic material

10.7498/aps.66.014204

∗国家自然科学基金(批准号:61205126)、湖南省科技计划项目(批准号:2016TP1021)和湖南省和湖南理工学院大学生实验项目(批准号:湘教通[2016]283号,校[2016]21号)资助的课题.

†通信作者.E-mail:zhaomingluo@hnu.edu.cn