微通道脉冲管中He气交替振荡的分子动力学模拟

芦 洋， 祁影霞,2， 陆熠璇, 车闫瑾， 刘雅丽， 陈卫谊

(1.上海理工大学 能源与动力工程学院， 上海 200093; 2.上海市动力工程多相流动与传热重点实验室， 上海 200093)

1 引 言

斯特林脉冲管制冷机具有结构简单、活动部件少、体积小、重量轻、使用寿命长等特点. 可满足医疗器械，红外探测器，超导量子干涉仪等精密仪器在低温工作环境的要求[1, 2]. 近几年，专家们对微型脉冲管制冷机进行了大量的研究[3-7]，Tang用100 Hz的频率来驱动直径为5 mm的脉冲管，该脉冲管的空载温度为49.5 K，在80 K时的冷却能力为1.7 W[8]. 研究结果表明，为了满足微型脉冲管制冷机的冷却要求，通常使用高频线性压缩机来提供功率[3, 9, 10]，高频脉冲管制冷机具有能量流密度大、热声效率高、振动和噪声小等特点. 因此，脉冲管制冷系统可以通过提高工作频率来进一步小型化. 对MPT中的微流过程和交替振荡的气体特性的研究可以增进对制冷机理的了解，为微通道脉冲管制冷机的结构优化提供基础.

Gan等人研究了线性压缩机的阻抗特性，优化了线性压缩机的运行机理和低温制冷系统中的阻抗匹配[11]. 杨森等人通过CFD仿真研究了脉管预冷对脉管内部温度场和速度场的影响，对脉管进行预冷会改变脉管工作时的内部温度分布,进而提高二级脉管制冷能力[12]. 巢伟等人利用REGEN 设计了一台单级大功率斯特林型脉管制冷机的回热器, 采用功效系数法对制冷量和COP进行了多目标优化,使得系统的性能最佳[13]. 王海敏等人采用SAGE对制冷机进行模拟，引入虚拟的振子阻尼调相机构对无负荷制冷温度进行模拟，结果表明30K时出现最佳制冷量[14]. 综上所述，向量分析方法主要使用正弦压力波和质量流波来演示小压力比的周期性物理特性，简化数值计算过程[11, 15]. CFD模拟方法需要预先设置恒定的进口边界值以及经验数据. 当流体被假定为连续介质时，校正系数用于描述湍流模型，因此与实际的交替振荡过程相比可能会有误差[16-20]. REGEN用于计算再生器[21, 22]，SAGE可以基于热声理论对整个设备进行一维数值模拟. 但是二次流和涡流的描述可能不准确[23, 24]，脉冲管内部的温度难以获得. 因此，压缩机声功率和冷端负荷的有效耦合方法理论仍然缺乏. 分子动力学模拟遵循经典的牛顿力学定律，可以重建原子运动演化过程. 非平衡分子动力学(NEMD)通常用于评估非稳态原子块，例如施加的力场，电场和磁场. NEMD可以在具有复杂流和许多分子的微系统中实现[25].

另外，实验中实际的流动过程和脉管参数的演变也难以监控和获取，阻碍了MPT数值模拟. 分子动力学方法只需要提供初始状态，例如时间，充气压力和整体温度，而不是操作过程中的过程点. 因此，在微观水平上用数字描述了管内温度梯度的变化. 结果表明，脉冲管的轴向压力和密度分布不均匀，这也是沿轴向温度梯度变化的原因. MPT气柱的声振动频率必须与线性压缩机的固有频率结合在一起，以建立合理的声场，以确保脉冲管的绝热膨胀效率. 由于缺乏理论和数值分析，实验数据被用于基于压缩机的扫气容积与MPT容积之比来指导设计. 因此，本文使用分子动力学方法建立了线性压缩机和脉冲管的模型，以便在微观水平上研究MPT的声场和温度梯度.

2 分子动力学模拟方法

分子的总能量是总势能U和总动能EK的总和. 总势能U通常包括分子的范德华力和内部势能. 分子之间的范德华力通常由力场描述. 这项研究中，在He原子之间使用了Lennard-Jones势能. 其中包括12次幂的排斥项与6次幂的吸引项. 如下所示：

(1)

式中，ε(eV)为原子间作用力，取0.000607098；σ(Å)为原子间距离，取2.103. 则系统内总势能可表示为：

(2)

通过原子的初始位置获得系统的总势能之后，就可以计算出原子在系统中的力和加速度[27, 28]. 并对时间进行积分，获得t+δt时刻的分子位置与速度,

(3)

(4)

Verlet算法用于求解递归方程，并根据位置的差分获得速度[10]：

(5)

(6)

当系统的平均温度用于赋予下一次循环中原子的初始速度，并由该时刻原子的坐标得到新的系统势能与动能，进行迭代计算：

(7)

(8)

当系统中设置为(NVE)系综时，那么系统中的压强是变量，相对应的公式可以计算出其压强与时均温度：

(9)

(10)

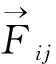
3 仿真模型分析

为了研究MPT的充气和放气过程之间的耦合机制，建立了包括线性压缩机和MPT的三维绝热模型. 使用非平衡分子动力学进行模拟计算. 压缩机内使用正弦速度活塞提供He气动力. 在X维度上使用了周期性边界，在Y(Yi和Yh)和Z(Zi和Zh)方向上使用了固定边界. 为了在轴向上区分结果，将模拟盒子沿管每100 nm分成一个格子，以获得实时的物理特性，例如温度和压力. Yh，Yi和Zh边界设为反弹壁面，使原子与反射壁之间发生完全弹性碰撞. 活塞直径和MPT直径相同. MPT尺寸为5.72 Å*2000 Å*17160 Å (x*y*z)，其中充满He气. 将移动的反射正弦速度壁面作为活塞放置在Zi处. 活塞的运动方向定义为Zi→Zh，其位移为572nm，因此其瞬时功能位置如公式11所示，

Z=A[1-cosω(tp-t0)dt]

(11)

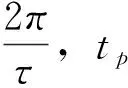
图1 在t=0和时的分子动力学模型Fig. 1 Molecular dynamics models at t=0 and

首先，在NVT系综(原子数、模型体积、温度不变)中，标定10万步以获得300 K的均匀温度分布. 接下来，在NVE系综中使用绝热模型来模拟MPT在0.4 fs的时间步长处的充气和放气过程. 根据Qi的研究[7]，1H-3L的脉管在压比为2时自然振荡周期为2240 ps. 振荡时间受充气压力[8, 26, 27]影响. 本研究中使用的时间和充气压力如表1所示(每个模型的名称包括两部分，分别涉及充气压力和时间. 例如，在A1中，模型的充气压力为 10 bar，时间为4000 ps).

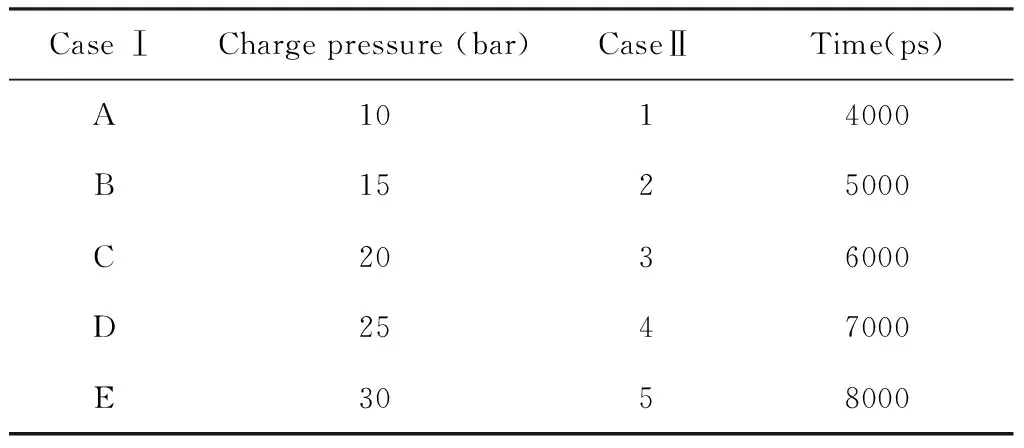
表1 模型参数

4 结果与讨论

4.1相位角

MPT中压缩与膨胀过程为等熵绝热过程. 由公式12可知冷却能力受压力波和质量流之间的相角影响[28, 29].

(12)

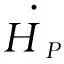
如图1所示，模型的左端是冷端，右端是热端. 如图2、图3所示，定义压力波超前质量流时相角为正值. 由仿真结果可知相角在冷端为正、热端为负. 冷端活塞位移与冷端压力波之间的相角为54°，仿真数据与实验结果一致[12,17,24].

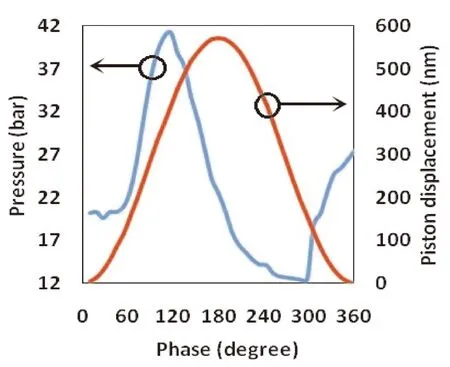
图2 模型C1活塞位移与冷端压力波之间的相角Fig. 2 The phase shift between the displacement of piston and the pressure curve at cold end of model C1

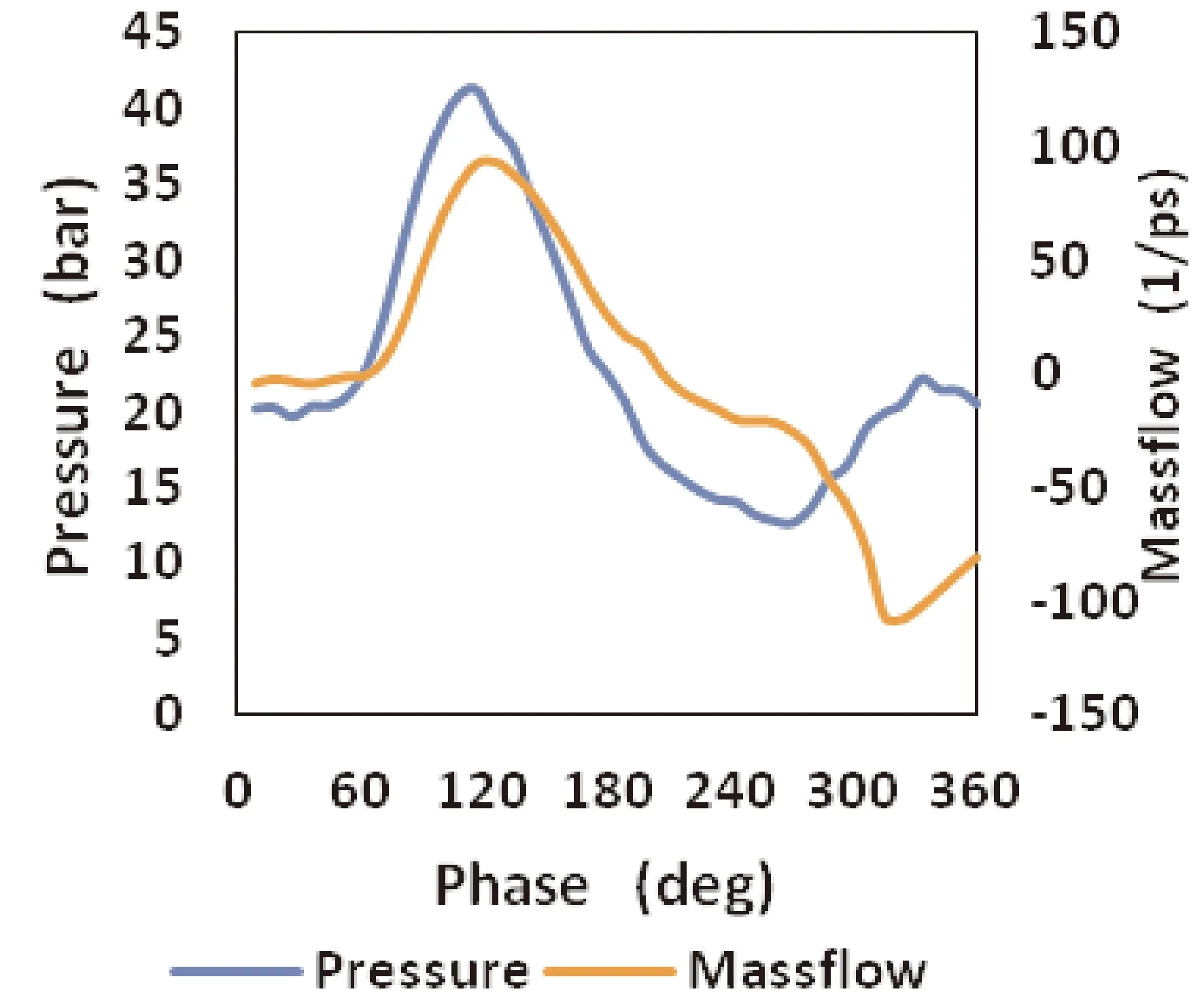
图3 模型C1冷端压力与质量流量之间的相角Fig. 3 The phase shift between the pressure curve and mass flow curve at cold end of model C1

4.2 MPT的冷却机制

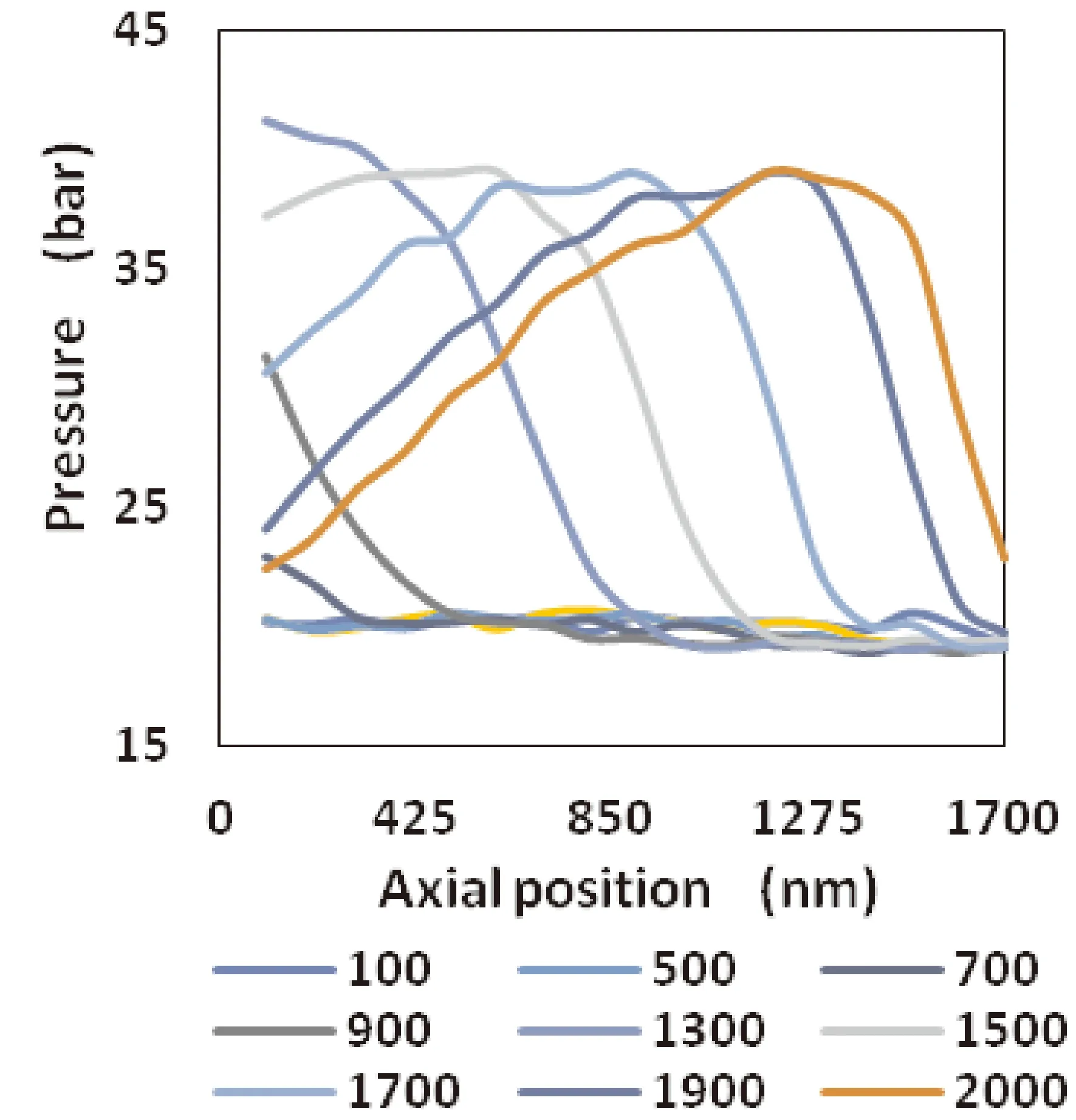
图4 模型C1压缩过程通道内轴向压力分布Fig. 4 The axial pressure distribution during compression process of model C1 in the tube

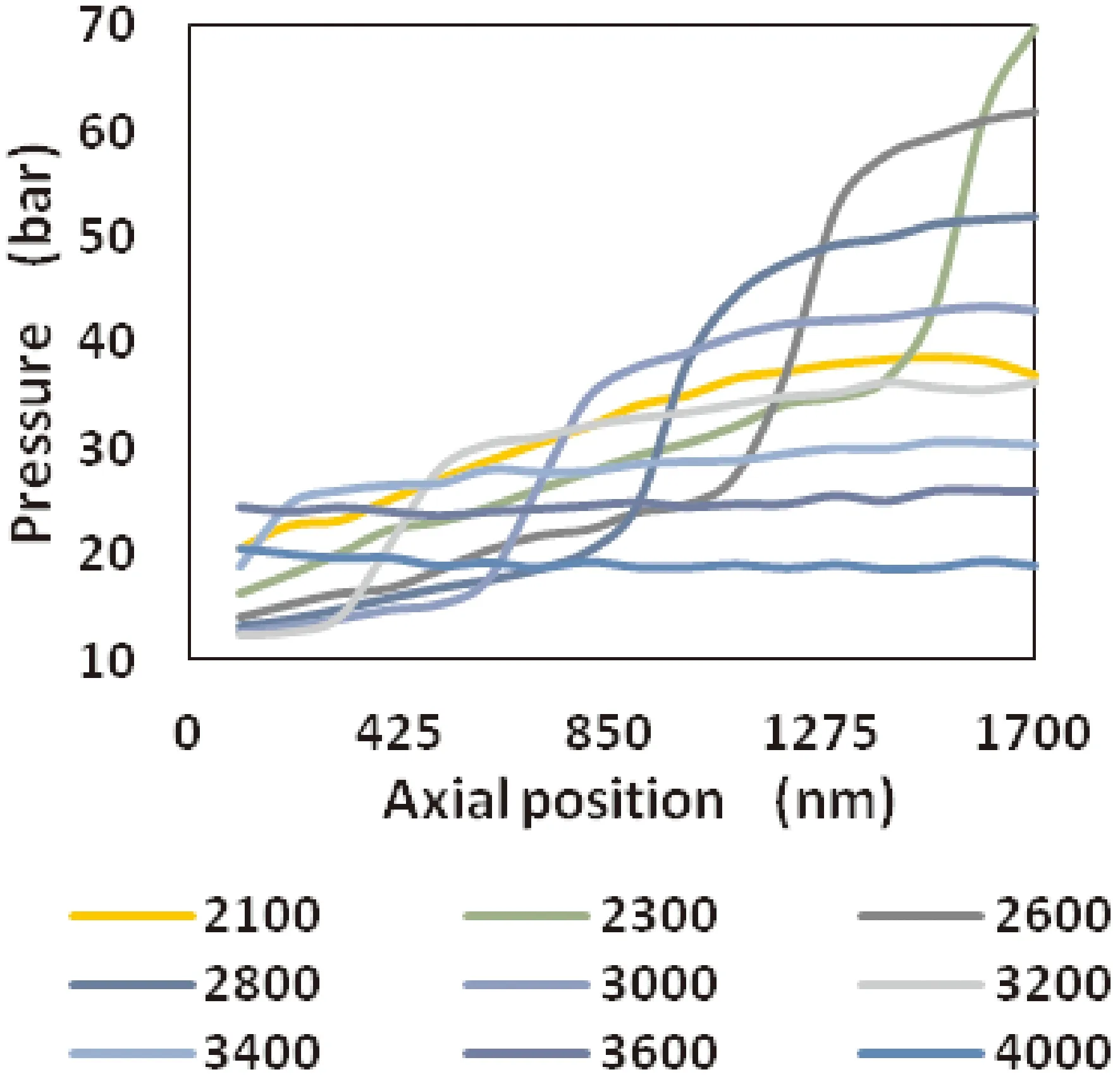
图5 模型C1膨胀过程通道内轴向压力分布Fig. 5 The axial pressure distribution during expansion process of model C1 in the tube

通过对压缩和膨胀过程作对比可获知，声波前压力梯度分布的动态传递过程是不对称的. 这是由于封闭的表面和气体消散声波的能量引起的. 在膨胀过程中， 活塞的反向运动导致冷端附近产生压差，产生绝热膨胀过程，从而导致冷端温度远低于300 K，而热端温度远高于300K. 在这种动态过程中，MPT中形成了不均匀的温度梯度，小孔型脉冲管制冷机(OPTC)和惯性管型脉冲管制冷机(ITPTC)将声波惯性从热端通过孔板或惯性管耗散到气库，而不是直接与封闭端造成碰撞.

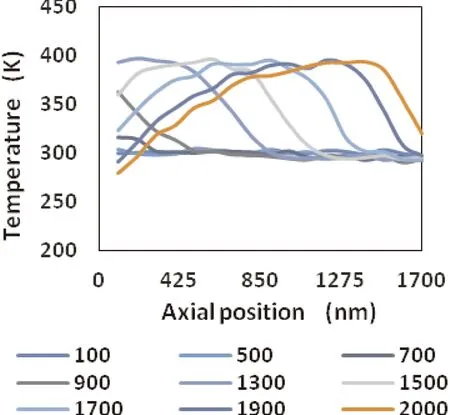
图6 模型C1压缩过程通道内轴向温度分布Fig. 6 The axial temperature distribution during compression process of model C1 in thetube

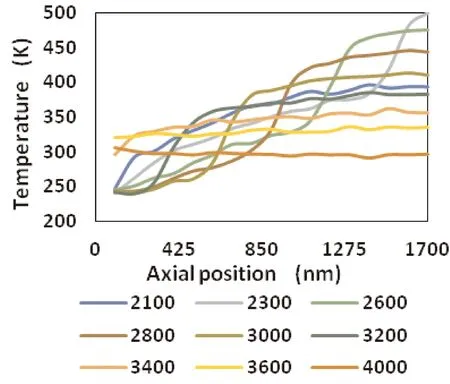
图7 模型C1膨胀过程通道内轴向温度分布Fig. 7 The axial temperature distribution during expansion process of model C1 in the tube

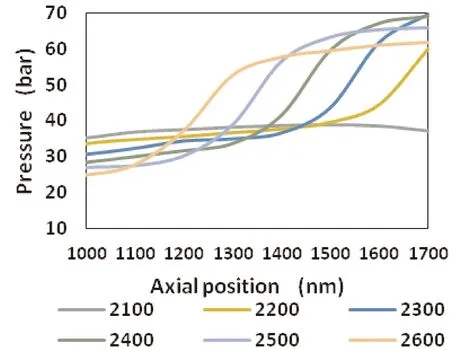
图8 模型C1中混流过程通道内的轴向压力分布Fig. 8 The axial pressure distribution during mixed flow process of model C1 in the tube

4.3 瞬时平均参数分析

如图10所示，测定循环中的冷端瞬时平均温度. 根据这项研究的模型，当τ≥6000 ps时，冷端的瞬时平均温度变化很小. 这表明MPT的声场建立过程与强制对流和气体振荡过程中压力梯度引起的自然对流有关. 自然对流强度与MPT的轴向压力梯度呈正相关. 当Po≤15 bar时，瞬时平均温度受强制对流时间的影响较小. 但是，在高压条件下(20 bar-30 bar)，当强制对流时间短于自然对流时间时，冷端温度随时间的降低而降低，如图11所示，最终进一步增加. 将回热器放置在MPT的前面，在反复的气体压缩和膨胀过程中，冷端的温度不断降低.

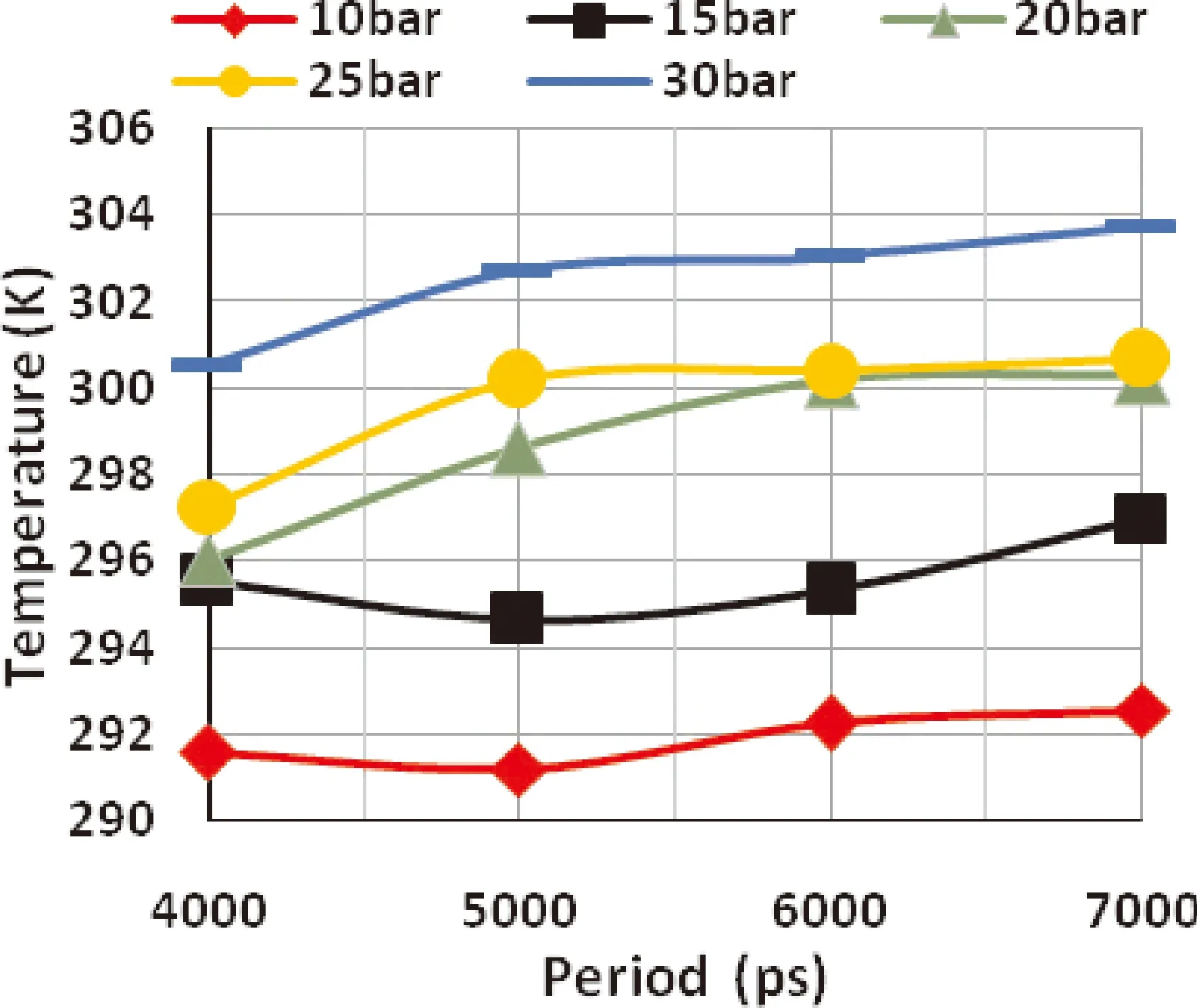
图10 不同时刻与充气压力下冷端的瞬时平均温度Fig. 10 Instantaneous average temperatures of the cold junction at different times and inflation

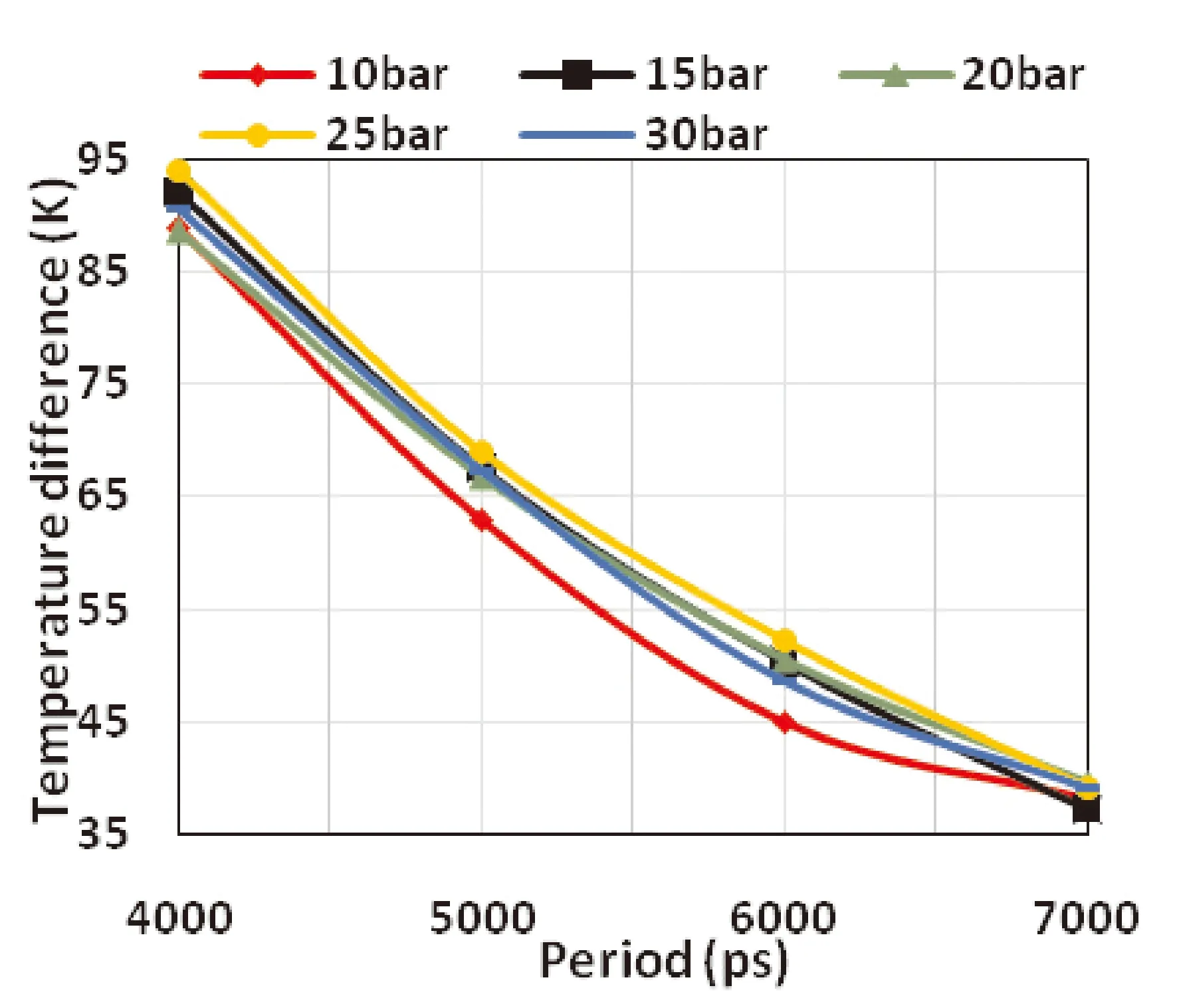
图11 不同时刻和充气压力下冷端和热端之间的时均温差Fig.11 Time-averaged temperature differences between cold and hot ends under different times and inflation pressures

综上所述，适当提高充气压力对冷却效果是有益的. 当运行频率高于MPT的固有频率时，冷端温度会进一步降低，但热端温度较高，因此对换热器和调相元件的散热量需求更大. 另外，回热器通常填充金属网或多孔介质，较高的运行频率会相应产生更高的流动阻力，增加回热器的摩擦损失与压降损失，因此，低流动阻力和高回热效率的回热器应成为下一阶段研究的重点. 该模型忽略了轴向表面的传热损失和表面之间的摩擦损失，从而导致轻微的误差[30].

5 结 论

用分子动力学方法模拟了微通道结构脉管中氦气的交变振荡过程，建立了宏观与微观状态参数之间的关联式. 仿真结果揭示了高频微通道脉冲管制冷机的微观机理，为设计MPT制冷机的结构和运行参数提供了理论依据.

(1) 随着时间的减少，MPT中出现了压力波传输特性，并且主压力梯度分布于波前. 在压缩过程中，从冷端传递到热端的压力波保持恒定的压力梯度值，在封闭端形成负压梯度且数值显著增加. 在膨胀过程中，压力梯度会随着时间连续下降. 随着时间的增加，平均压力分布与轴向压力梯度分布交替出现，梯度值恒定的压力波消失，因此多重振荡过程影响了冷却效果.

(2) 声波传输效应是建立冷却效应和轴向温度梯度的关键. 冷端温度对强制对流时间和充气压力敏感，对高压更敏感. 当强制振荡周期的时间短于与自然振荡周期相同的压力时，冷端的温度进一步降低，而热端的温度升高. 这也是为什么高频斯特林脉冲管制冷机在冷端具有更高的冷却能力和更低的空载温度的原因.

(3) MPT相移约为20°至40°. 最佳高充气压力周期小于低充气压力周期，较短的时间导致声波传输更大的能量流密度，因此声波两侧的压力梯度值都较大. 较大的压比有利于制冷，但必须具有较高性能的换热器. 仿真结果揭示了高频微通道脉冲管制冷机的微观机理，为设计MPT制冷机的结构和运行参数提供了理论依据.