自旋三重态Sr2RuO4超导能隙的p波对称性
2013-10-27王琼,李铭
王 琼, 李 铭
(华南师范大学物理与电信工程学院,量子信息技术实验室,广东广州 510006)
自旋三重态Sr2RuO4超导能隙的p波对称性
王 琼, 李 铭*
(华南师范大学物理与电信工程学院,量子信息技术实验室,广东广州 510006)
在三带模型下,考虑带间和带内的在位库伦排斥、洪特耦合以及带内的配对耦合势,采用RPA近似求解能隙方程,得到了Sr2RuO4三个能带上的自旋三重态能隙.计算结果表明,相互作用势在格点上表现为在位的排斥,以及近邻和次近邻格点之间的吸引.xy轨道的配对势近似呈四重旋转对称,而yz和zx轨道的配对势明显以横向方式展开,呈二重旋转对称.同时,在自旋涨落和电荷涨落作用下,电子之间的自旋三重态配对能成功再现Sr2RuO4的p波形式的能隙结构.随着温度上升,能隙逐渐减小到0,得到转变温度与实验结果基本一致.
自旋三重态; p 波超导能隙; Sr2RuO4
非传统超导主要集中在重费米子超导体系列[1]、铜氧化物超导体系列[2]、有机超导体系列[3]、Ruthenate超导体系列[4]以及铁基超导体系列[5]等.这些超导体不同于传统的低温超导体,其区别主要表现在非电声子相互作用机制不同,另外,能隙都具有各向异性,而传统超导体的能隙都是各向同性的s波形式. 多数非传统超导体跟传统超导体的相似之处是:库伯对的配对形式都是自旋单态.但是,也有少数非传统超导体是自旋三重态配对的. 它们可能分布在上述多个系列中(实验上尚有争议). 这种配对形式在费米液体3He超流中已经成功建立起来. 现在,实验证实Sr2RuO4也是自旋三重态配对的[4,6]. 这是非传统超导体中非常特殊的一类超导体,因而一直受到凝聚态物理理论界的高度重视.自旋三重态配对时,Sr2RuO4的配对波函数的轨道部分是交换反对称的.Sr2RuO4具有跟铜氧化物一样的平面结构,但其超导转变温度只有1.5 K,各向异性比达到20倍,层内的相干长度比层间大几倍.实验上人们通过核磁共振(NMR)[7]和μSR[8]等技术测量出Sr2RuO4具有手征的p波序参量[9]. 近年来,随着实验技术的进步,人们对Sr2RuO4的能隙、序参量对称性以及超导特性进行了更精密的测量,进一步确认了它的p波对称性[10]. 理论上,人们对Sr2RuO4的自旋三重态配对进行了大量研究[11-13]. 普遍认为,电子之间的强关联特别是在位的库伦排斥阻止了传统的s波配对在Sr2RuO4中的形成.迄今为止,人们对Sr2RuO4的配对机制研究主要是如下6个方面:1)铁磁自旋涨落;2)各向异性的反铁磁自旋涨落;3)非公度的电荷和轨道涨落;4)Ru的4d轨道电子的洪特耦合;5)更远格点间的相互作用;6)同格点上的库伦排斥[10]. 上述机理都与实验不完全吻合.最近,RAGHU等[12]仅仅考虑在位的带内和带间排斥,通过两能带模型计算了Sr2RuO4的自旋三重态配对,得到能隙函数近似为Δxz=Δ0sinkx×cosky,Δyz=Δ0sinkycoskx,但也包含一些高阶成分. 计算结果表明,Sr2RuO4的自旋三重态配对比自旋单重态配对更稳定. 但是,计算过程没有考虑带间的耦合、洪特耦合、配对跳跃等其他相互作用成分.2002年,TAKIMOTO[13]考虑了这些相互作用,通过无规位相近似(RPA)方法计算出的能隙函数具有p 波对称性,但横向分布与RAGHU等[12]的结果不一致. 因而,利用新的能带参数重新计算超导能隙的对称性是有必要的. 能带计算表明,Sr2RuO4有3个费米面,对Sr2RuO4的电子结构有重要作用.
本文采用RAGHU等[12]建立的三带模型,利用RPA近似对Sr2RuO4的能隙进行进一步的研究,揭示自旋三重态配对下Sr2RuO4的能隙对称性.
1 RPA近似下的理论模型
1.1 哈密顿量
采用的三带哈伯德模型[13]包含4个相互作用项,即耦合常数分别是带内电子库伦排斥U、带间电子库伦排斥U′、电子之间洪特耦合J及配对跳跃J′:
H=H0+HI,
(1)
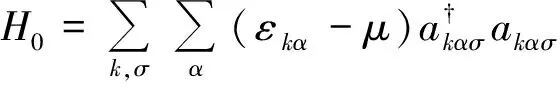
(2)
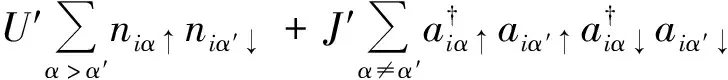
(3)
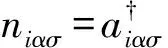
ε1=-2tx1coskx-2ty1cosky+4t1coskxcosky,
(4)
ε2=-2tx2coskx-2ty2cosky,
(5)
ε3=-2ty2coskx-2tx2cosky,
(6)
其中,tx1=0.8,ty1=0.8,t1=-0.3,tx2=1.0,ty2=0.1,μ=1.0.经过RPA近似,上述相互作用近似为下列有效相互作用哈密顿量:
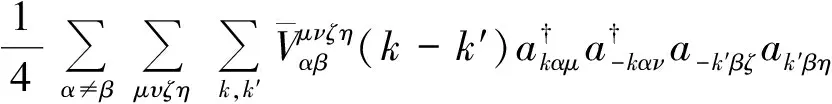
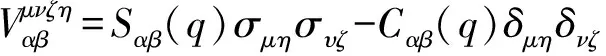
(7)
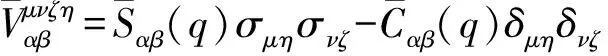
(8)
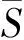

(9)
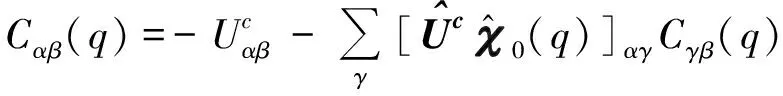
(10)
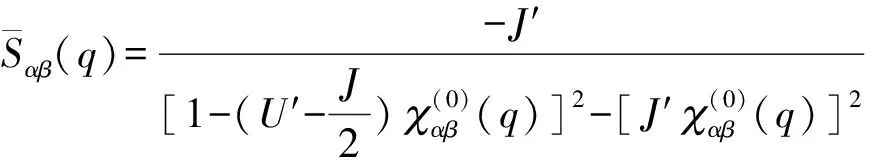
(11)
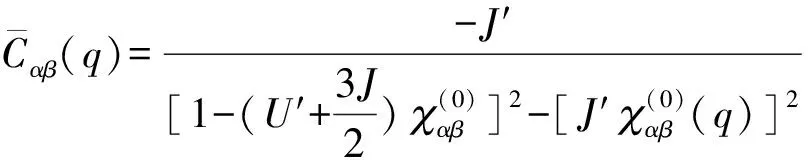
(12)
其中S(q)和C(q)分别描述系统的自旋涨落和电荷涨落,
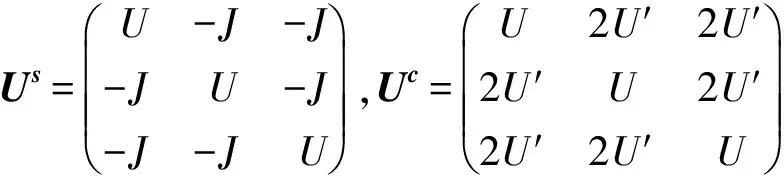
(13)
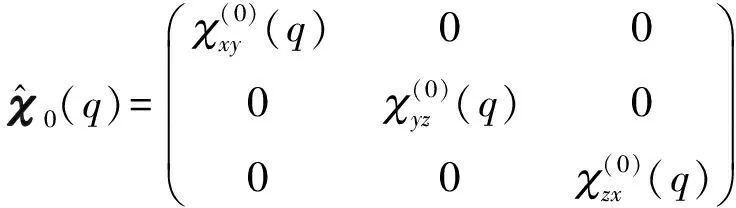
(14)
(15)
其中f(ε)=1/(eβ(ε-μ)+1)是费米分布函数,β=1/(kT).
1.2 能隙
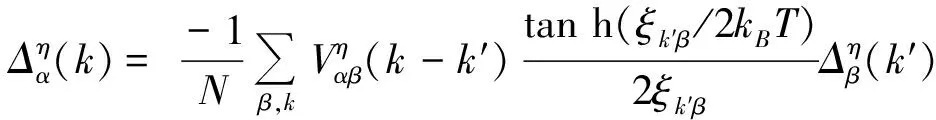
(16)
其中
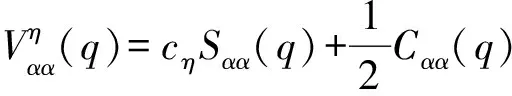
(17)
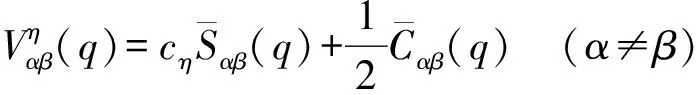
(18)


2 计算结果与讨论
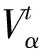
图3显示了xy轨道和yz(zx)轨道上能隙最大值随温度的变化,由能隙下降的趋势可近似得到转变温度为kBTC≈0.002 3tx2. 其他参数同图1.xy轨道上的能隙显著大于yz和zx轨道上的能隙. 随着温度的上升,能隙几乎呈线性下降,当温度接近转变温度区域时,能隙迅速下降到0. 由此可得转变温度约为kBTC≈0.002 3tx2.

图1 在RuO2平面上各个格点的自旋三重态相互作用势Figure 1 The interaction potential on the RuO2

3 结论
在三带模型下,考虑带间和带内的在位库伦排斥,洪特耦合以及带内的配对耦合势,在RPA近似下将相互作用近似为自旋涨落和电荷涨落,通过求解能隙方程,得到了3个能带上的自旋三重态能隙. 计算结果表明,自旋涨落和电荷涨落引起的配对势在格点上表现为在位的排斥,以及近邻和次近邻格点之间的吸引.xy轨道的配对势近似呈四重旋转对称,但yz和zx轨道的配对势显著地横向展开,呈二重旋转对称.xy轨道上能隙沿对角线方向,具有sinkx-sin(2kx)+sinky-sin(2ky)的p波形式;而yz轨道上能隙具有sinky-sin(2ky)的p波形式.随着温度的上升,能隙逐渐减小到0,得到转变温度约为kBTC≈0.002 3tx2. 可见,在自旋涨落和电荷涨落作用下,电子之间的自旋三重态配对能成功再现Sr2RuO4的p波形式的能隙结构.

图3 xy和yz(zx)轨道上能隙最大值随温度的变化
[1] STEGLICH F, AARTS J, BREDL C D, et al. Superconductivity in the presence of strong Pauli Paramagnetism: CeCu2Si2[J]. Phys Rev Lett, 1979, 43: 1892-1896.
[2] BEDNORZ J G, MULLER K A. Possible high Tc superconductivity in Ba-La-cu-O system[J]. Z Phys, 1986, B64: 189-193.
[3] JEROME D, MAZAUD A, RIBAULT M, et al. Superconductivity in a synthetic organic conductor (TMTSF)2PF 6[J]. J Phys Lett,1980, 41: 95-98.
[4] MAENO Y, HASHIMOTO H, YOSHIDA K, et al. Superconductivity in a layered perovskite without copper[J]. Nature,1994,372:532-536.
[5] KAMIHARA Y, WATANABE T, HIRANO M, et al. Iron-Based layered superconductor La[O1-xFx]FeAs (x=0.05-0.12) with Tc=26 K[J]. J Am Chem Soc, 2008, 130: 3296-3297.
[6] MACKENZIE A P, MAENO Y. The superconductivity of Sr2RuO4and the physics of spin-triplet pairing[J]. Rev Mod Phys, 2003, 75:657-661.
[7] ISHIDA K, MUKUDA H, KITAOKA Y, et al. Spin-triplet superconductivity in Sr2RuO4identified by 17O Knight shift[J]. Nature, 1998, 396:658-660.
[8] LUKE G M, FUDAMOTO Y, KOJIMA K M, et al. Time-reversal symmetry-breaking superconductivity in Sr2RuO4[J]. Nature, 1998, 394: 558-561.
[9] RICE T M. Superconductivity: An analogue of superfluid3He[J]. Nature,1998, 396: 627-629.
[10] MAENO Y, KITTAKA S, NOMURA T, et al. Evaluation of Spin-Triplet Superconductivity in Sr2RuO4[J]. J Phys Soc Jpn, 2012, 81: 1-31.
[11] MONTHOUX P, LONZARICH G G. Magnetic interactions in a single-band model for the cuprates and ruthenates[J].Phys Rev B, 2005, 71: 054504.
[12] RAGHU S, KAPITULNIK A, KIVELSON S.Hidden Quasi-one-dimensional Superconductivity in Sr2RuO4[J]. Phys Rev Lett, 2010, 105:136401.
[13] TAKIMOTO T. Orbital fluctuation-induced triplet superconductivity:Mechanism of superconductivity in Sr2RuO4[J]. Phys Rev B, 2000, 62: R14641.
Keywords: spin triplet; p-wave superconducting gap; Sr2RuO4
Thep-WaveSymmetryoftheSuperconductingGapsofSr2RuO4intheSpinTripletState
WANG Qiong, LI Ming*
(Department of Physics, Laboratory of Quantum Information Technology, School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China)
The spin triplet gaps of the three orbitals of Sr2RuO4are obtained by solving the gap equation in the random phase approach. The on-site inter- and intra-band Coulumb repulsion, the Hund’s coupling and the intra-band pairing are considered in the approach. The computation shows that the pairing couplings induced by the spin and charge fluctuation are on-site repulsive and attractive between the neighboring and the next neighboring sites. The pairing coupling of thexyorbital is four-folded symmetric and those of theyzandzxorbitals are two-folded symmetric. As the temperature increases, the gaps decrease to zero at a transition temperature ofkBTC≈0.002 3tx2.
2012-04-03
国家自然科学基金项目(10874049);广东省自然科学基金项目(07005834)
*通讯作者:李铭,副教授,Email:wliming@scnu.edu.cn.
1000-5463(2013)01-0047-04
O157.5
A
10.6054/j.jscnun.2012.12.009
【中文责编:谭春林,庄晓琼 英文责编:肖菁】
