难点剖析把脉 思路设计突破

摘  要：文章就一道中考压轴题的最后一问进行解题教学尝试，以学生的视角进行探讨，剖析学生思路受阻的原因，真实还原学生解题时面临的难点和盲点. 根据试题所蕴含的核心概念及其外延展开教学设想，设计系列问题推动教学探究，旨在逐一突破难点，并提炼解决此类问题的一般方法与基本“套路”，努力提升学生分析问题和解决问题的能力.

关键词：解题教学;精准设计;教学设想

中考压轴题的最后一问通常是对学生数学能力的综合考查，不仅为学生综合运用知识、深度学习、展现数学学科核心素养提供了很好的展示机会，还对学生分析问题和解决问题的能力提出了更高的要求. 如何让学生快速获取正确的解题思路？怎样才能突破与优化解法？如何真正让学生领悟试题所承载的本质？其实，解法隐于问题内部，来源于试题本身. 我们不妨以学生的视角进行解题分析，真实还原学生解题时面临的难点和盲点. 针对学生的解题困境，精准设计系列问题，把问题解决、经验积累与思想渗透有机结合起来，引导学生发现和思考，获得可视化思维路径，展现解法的发现历程.

一、试题呈现

题目 （2019年湖北·十堰卷）已知抛物线[y=][ax-22+][c]经过点A[-2，0]和[C0， 94，] 与x轴交于另一点B，顶点为D.

（1）求抛物线的解析式，并写出点D的坐标.

（2）如图1，点E，F分别在线段AB，BD上（点E不与点A，B重合），且[∠DEF=∠A，] 则[△DEF]能否为等腰三角形？若能，求出BE的长;若不能， 试说明理由.

（3）若点P在抛物线上，且[S△PBDS△CBD]= m，试确定满足条件的点P的个数.

二、难点剖析

本文只针对第（3）小题进行分析讨论. 第（3）小题以抛物线上架构的三角形为载体，以动（静）态三角形面积计算为媒介，重点考查函数图象中面积计算问题的常规解题思路，以及转化与数形结合思想的运用. 在实际解题中，学生可能遇到以下几个难点.

难点1：如何计算抛物线内接三角形的面积？对于确定的三角形（静态的三角形，如△CBD），如何计算其面积？解题的依据是什么？有多少种求解方法？对于动态三角形（如△PBD），又将如何处理呢？因此，如何准确、快速地计算出三角形的面积是确保问题顺利解决的首要条件.

难点2：由于点P的位置具有不确定性，加大了学生计算△PBD面積的难度，阻碍了部分学生继续前进的“步伐”. 因此，题目的难点还在于学生能否考虑到对点P的具体位置进行分类讨论，并在此基础上围绕点P的运动进行画图分析，感受化动为静的过程，以及点P位置的改变导致求S△PBD方法的多样与优化. 如何分类？分类界点在哪里？分类后又将如何计算？特别值得一提的是，学生对分类后“点P在直线BD的下方”这种情形下的面积计算感到困难.

难点3：关于点P个数的求法，现行教材中没有类似的例、习题可以借鉴. 由于学生缺少解决此类问题经验的积累（包括用几何画板软件演示等操作经验的积累），普遍对“对于每个确定△PBD面积的点P，在抛物线上是否必定存在关于直线BD的对称点？”“存在几个点P？”“根据什么来确定点P存在的个数？”等问题感到困惑.

难点4：此题最大的难点在于学生对[S△PBDS△CBD=m]的理解. 如何看待m？如何感受m的取值与点P的个数间存在的必然联系？这就需要有效地拆解条件，并思考：如何从形式上加以简化？如何从内涵上加以转化？如何用函数的眼光去解决问题？

首先，从“形”入手. 从图象直观感知三角形的面积有如下变化规律：由于点C，B，D为三个定点，故分母S△CBD必为一个确定的值;再看分子，由于点P，B，D为“一个动点 + 两个定点”，故需要对点P的位置进行分类讨论. 结合图象，当点P在直线BD的上方（右侧）时，发现S△PBD存在最大值;当点P在直线BD的下方（两侧）时，发现S△PBD的面积随x的增大而增大（或减小）. 其次，从“数”入手，运用函数解析式找准面积之间的数量关系. 如果动点P的横坐标用参数n表示，那么S△PBD可以用含参数n的代数式来表示. 可以挖掘出如下一般规律：如果用参数n表示点P的横坐标，那么m就可以看作是一个关于n的二次函数. 最后，数形结合，精准定位m的取值与点P个数的对应关系.

基于学生面临的诸多难点的分析，我们有必要针对第（3）小题所蕴含的核心概念，以专题的形式对“面积及计数问题”展开教学设计，设计精准的问题系列推动教学探究，使学生逐一突破难点，提升学生分析问题和解决问题的能力.

三、教学设计

环节1：情境引入.

引例  如图2，已知二次函数y = ax2 + bx + c的图象与x轴交于A，B两点，点A[-1，0]，与y轴交于点C，且抛物线的顶点D[1，4]. 观察图象，你能得出哪些结论？

【设计意图】设置联想式例题，便于学生主动参与，引导学生进行交流，并对所得的结论进行归类整理. 这些结论的获得为后续学习“探究三角形面积的计算”做了很好的铺垫.

环节2：问题探究.

问题探究1：如何计算△BCD的面积？

预设解法1（直接计算法）：求出△BCD各条边的长，发现△BCD为直角三角形，运用三角形的面积公式求解.

预设解法2（割补法）：如图3，过点D作[DE⊥Oy]于点E，由[S△BCD=S梯形OBDE-S△BOC-S△CDE]来求解.

预设解法3（割补法）：如图4，连接OD，由[S△BCD=][S△OCD+S△OBD-S△BOC]来求解.

预设解法4（铅锤法）：如图5，过点D作[DF⊥Ox]交BC于点F，所以[S△BCD=12DF ⋅ OB].（如图6，三角形面积等于水平宽与铅垂高乘积的一半，即[S△BCD=12ah].）

【设计意图】问题探究1针对难点1而设计，让学生感受静态三角形面积求解的一般思路，比较多种求解方法.

问题探究2：若点P是抛物线在第一象限的一个动点，使得S△BCP = S△BCD，求满足条件的点P的坐标.

预设解法1（计算法）：如图7，分别过点D，P作y轴的平行线，交直线BC于点F，M，设点P的横坐标为n[1<n<3]，利用含参数n的代数式表示线段PM的长，根据PM = DF = 2，即可求得点P的坐标.

预设解法2（平行线法）：如图8，过点D作BC的平行线交抛物线于点P，求出直线DP与抛物线的交点坐标即可.

【设计意图】通过计算面积值确定的动点坐标，让学生感受动态三角形面积求解的一般思路，以及从“数——计算”“形——平行线”两种不同思维方式解法上的创新.

问题探究3：若点P是抛物线上任意一点，使得S△BCP = S△BCD，求满足条件的所有点P的坐标.

预设解法1（计算法）：如图9，分别过点D，P作y轴的平行线，交直线BC于点F，M，设点P的横坐标为n，利用含参数n的代数式表示线段PM的长，根据PM = DF = 2，即可求出点P的坐标.

预设解法2（平行线法）：如图10，过点D作BC的平行线，分别与y轴、抛物线交于点[E，P1，] 作点E关于点C的对称点[E]，过点[E]作直线BC的平行线，交抛物線于点P2，P3，则点P1，P2，P3即满足条件的点P. 通过联立方程组即可求出点P1，P2，P3 的坐标. 或者将点D向下平移4个单位长度亦可.

【设计意图】问题探究3针对难点2而设计，解决当点P在直线BC下方的抛物线上时的情形.

问题探究4：若点P是抛物线在第一象限的一个动点，记△BCP的面积为S，求S的取值范围.

预设解法1（割补法）：如图11，连接OP，设点P的横坐标为n，利用含参数n的代数式表示△BCP的面积，根据函数的性质求得△BCP的面积的最大值，进而求得S的取值范围.

预设解法2（铅锤法）：如图12，过点P作y轴的平行线交直线BC于点G，设点P的横坐标为n， 利用含参数n的代数式表示△BCP的面积，根据函数的性质求得△BCP的面积的最大值，进而求得S的取值范围.

预设解法3（平行线法）：如图13，过点P作直线BC的平行线，引导学生发现“当此平行线与抛物线有且仅有一个交点时，△BCP的面积最大”，进而求得S的取值范围.

问题探究5：若抛物线上有且仅有三个点P1，P2，P3，使得△P1BC，△P2BC，△P3BC的面积均为定值S，求出定值S及P1，P2，P3三个点的坐标.

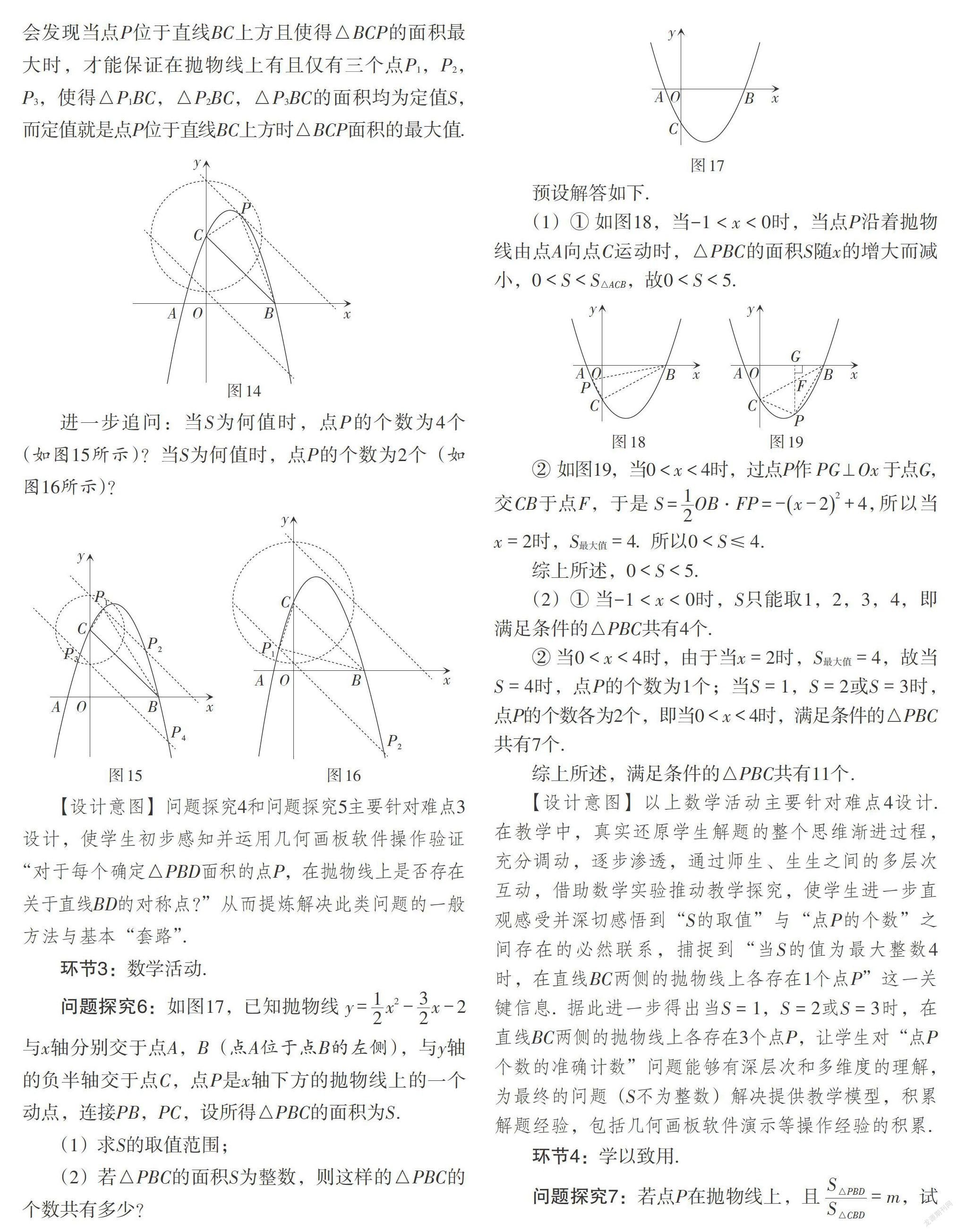
预设解法：如图14，经过问题探究4的学习，学生会发现当点P位于直线BC上方且使得△BCP的面积最大时，才能保证在抛物线上有且仅有三个点P1，P2，P3，使得△P1BC，△P2BC，△P3BC的面积均为定值S，而定值就是点P位于直线BC上方时△BCP面积的最大值.

进一步追问：当S为何值时，点P的个数为4个（如图15所示）？当S为何值时，点P的个数为2个（如图16所示）？

【设计意图】问题探究4和问题探究5主要针对难点3设计，使学生初步感知并运用几何画板软件操作验证“对于每个确定△PBD面积的点P，在抛物线上是否存在关于直线BD的对称点？”从而提炼解决此类问题的一般方法与基本“套路”.

环节3：数学活动.

问题探究6：如图17，已知抛物线[y=12x2-32x-2]与x轴分别交于点A，B（点A位于点B的左侧），与y轴的负半轴交于点C，点P是x轴下方的抛物线上的一个动点，连接PB，PC，设所得△PBC的面积为S.

（1）求S的取值范围;

（2）若△PBC的面积S为整数，则这样的△PBC的个数共有多少？

预设解答如下.

（1）① 如图18，当-1 < x < 0时，当点P沿着抛物线由点A向点C运动时，△PBC的面积S随x的增大而减小，0 < S < S△ACB，故0 < S < 5.

② 如图19，当0 < x < 4时，过点P作[PG⊥Ox]于点G，交CB于点F，于是[S=12OB ⋅ FP=-x-22+4，]所以当x = 2时，S最大值 = 4. 所以0 < S[≤] 4.

综上所述，0 < S < 5.

（2）① 当-1 < x < 0时，S只能取1，2，3，4，即满足条件的△PBC共有4个.

② 当0 < x < 4时，由于当x = 2时，S最大值 = 4，故当S = 4时，点P的个数为1个;当S = 1，S = 2或S = 3时，点P的个数各为2个，即当0 < x < 4时，满足条件的△PBC共有7个.

综上所述，满足条件的△PBC共有11个.

【设计意图】以上数学活动主要针对难点4设计. 在教学中，真实还原学生解题的整个思维渐进过程，充分调动，逐步渗透，通过师生、生生之间的多层次互动，借助数学实验推动教学探究，使学生进一步直观感受并深切感悟到“S的取值”与“点P的个数”之间存在的必然联系，捕捉到“当S的值为最大整数4时，在直线BC两侧的抛物线上各存在1个点P”这一关键信息. 据此进一步得出当S = 1，S = 2或S = 3时，在直线BC两侧的抛物线上各存在3个点P，让学生对“点P个数的准确计数”问题能够有深层次和多维度的理解，为最终的问题（S不为整数）解决提供教学模型，积累解题经验，包括几何画板软件演示等操作经验的积累.

环节4：学以致用.

问题探究7：若点P在抛物线上，且[S△PBDS△CBD]= m，试确定满足条件的点P的个数.（题目第（3）小题）

经验引领下的试题分析如下.

（1）设点P的横坐标为n，计算S△CBD的值，并用含参数n的代数式表示S△PBD.

（2）计算特定情况下m的值. 当点P在直线BD的上方时，易求得[m=-112n-42+13]. 当n = 4时，m有最大值[13]，故[m=13]是点P个数的分界值.

（3）借助实验得出结论. 如图20，当m =[13]时，满足条件的点P的个数为3个，即直线BD上方的抛物线上只有1个点P，而直线BD下方的拋物线上有2个点P.

如图21，当0 < m <[13]时，满足条件的点P的个数为4个，即在直线BD上方、下方的抛物线上各有2个点P.

如图22，当m >[13]时，满足条件的点P的个数为2个，此时点P只在直线BD下方的抛物线上，且只有2个点P.

四、结束语

数学离不开解题，但不能简单地只为解题而解题. 当学生非常顺利地解答问题时，教师应多提问学生. 例如，还有没有更好的方法？你能发现什么有趣的结论？当学生面对难题“卡壳”、一筹莫展时，教师可以适当停留，和学生一起回归试题本源，站在学生的角度分析条件、寻找原因，多问几个问题. 例如，你想到了什么？你是怎么想到的？以学生的视角进行解题分析，真实还原学生解题时面临的难点和盲点.

教师更应针对学生的解题困难、客观存在的挫折为契机，精准设计符合学生实际、贴近学生现实的问题及问题链，以解惑、答疑、重塑知识体系为目标，开展丰富的解题活动（本文从学生最为熟悉的“抛物线内接三角形面积计算”出发），让学生从已有的知识结构开始展开联想与尝试，帮助学生理清思路、梳理思维、寻找突破口，引导学生对试题涉及的知识及蕴涵的数学思想方法进行概括，归纳知识与方法的本质特征，最终让大多数学生接受且问题得到完美解决，并从中获得必要的经验与成就感，提升学生现场、限时分析问题、解决问题的能力.

参考文献：

[1]罗增儒. 学会学解题：写在《数学解题学引论》第4次印刷[J]. 中学数学教学参考，2004（9）：16-18.

[2]钱莉莉，王强强. 深挖试题内涵  追求解题价值[J]. 中国数学教育（初中版），2012（6）：34-38.

[3]郭玉峰，史宁中.“数学基本活动经验”研究：内涵与维度划分[J]. 教育学报，2012，8（5）：23-28.

[4]司友军. 抽丝剥茧  层层递进：一类几何动点问题的解法分析[J]. 中学数学教学参考（中旬），2019（6）：35-37.