基于材料相变的声子晶体带隙可调结构设计与性能分析

(大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116024)

1 引 言

声子晶体(PCs)作为一种新型功能材料[1]，由于其独特的性能和重要的应用潜质，受到国内外研究者的广泛关注，成为研究热点。弹性波在PCs中传播时，受其内部结构的作用，在一定频率范围(带隙)内无法传播，而在其他频率范围(通带)可以无损耗地传播。研究发现，声子晶体带隙产生的机理主要包括布拉格散射和局域共振2种。前者主要是周期性结构的作用，当入射弹性波的波长与结构的特征长度(晶格常数)相近时，将受到结构强烈的散射[2]。后者主要是单个散射体的共振特性起主导作用[3]。PCs在设计新型声学器件如滤声器、声波导和隔振器等方面具有很大的潜力[4-6]。传统的声子晶体存在特定的带隙性质和确定的工作频率范围[7]，且由其几何构型和材料性质确定。但对于特殊的应用环境，随着环境的变化需要满足在不同频率下阻断波的传播的需求，需要声子晶体具有带隙频率和位置的可调性。通过施加诸如电磁场[8]、拉伸变形[10]和变化的温度场[11]等方式可实现带隙可调控。研究建立可调带隙声子晶体的设计方法，研究并提出创新构型，通过施加外部激励，实现声子晶体的带隙可调，已经成为重要的研究热点。

本文目的基于带隙产生的机制和影响参数分析，建立实现智能调控带隙的方法，进一步设计可调的PCs。

形状记忆合金(SMA)作为一种超材料，其材料性质和几何构型可以随温度和应力发生变化[12]，这为声子晶体带隙可调的发展提供了一个崭新的契机。目前研究者已经开展了一些基于形状记忆合金的声子晶体设计方面的工作。Ruzzene等[13]将SMA周期性放置在复合材料杆中，作为阻抗失配插入物，以控制纵波在复合材料杆中的传播。当SMA由马氏体向奥氏体相变，其弹性模量可以发生变化，进而实现带隙可调。de Sousa等[14]基于谐振器的马氏体相(低温)和奥氏体相(高温)弹性模量的差异，带隙随着温度变化发生明显移动并对含SMA谐振器的局部共振梁进行了实验验证。Lü等[15]将SMA作为智能插入件，设计可以产生可调带隙的结构，利用集中质量法在SMA梁上实现了带隙可调，值得注意的是，采用的是单向形状记忆的SMA，材料性质发生改变，形状没有变化。Chuang等[16]设计了一种具有双向SMA谐振腔的可调弹性超材料。可以在局域共振带隙和布拉格散射带隙不同的带隙机制之间相互切换，这是通过SMA形状的变化和SMA谐振器刚度的变化实现了带隙的可切换。然而，几乎所有研究都主要集中在一维PCs上，而高维(2D或3D)声子晶体具有更重要的应用潜质。本文提出一种基于形状记忆合金相变的穿孔型带隙可调2D声子晶体结构，通过合理布置缝隙与形状记忆合金相材料的位置，实现声子晶体带隙性质的可调设计。基于有限元方法，建立可调声子晶体的分析模型，分析形状记忆合金填充分数以及相变等对带隙性能的影响规律。通过具体设计和性能分析，验证材料相变可实现带隙位置和宽度的调节以及特定频段内带隙的有无。

2 可调带隙声子晶体结构设计

如图1所示，二维声子晶体为环氧树脂型基体平板内镶嵌相变材料(本文取相变材料为形状记忆合金)，通过温度调节使相变材料发生相变，从而改变其材料性质，实现声子晶体带隙性质可调。本文所设计的可调带隙声子晶体的单胞结构为正方形环氧树脂平板中镶嵌正方形形状记忆合金散射体，其晶格常数为L，如图1(b)所示。为更大程度地实现更低更宽及更易调控的带隙，在方形板的周围设计了细窄的矩形缝隙，其长和宽分别为a和b。散射体边长为c，其填充分数可以表示为4c2/(L2-4ab)。形状记忆合金有两种形态，一种是低温状态下马氏体相，另一种是高温状态下的奥氏体相。两种状态具有不同的材料性质。通过温度变化，实现形状记忆合金状态转换。通过状态转换引起材料性质的变化(散射体材料性质变化)，实现带隙性质的变化。通过控制温度，进而控制相变转化程度，从而控制散射体的材料性质的变化，实现带隙调控。本文设计采用NiTi形状记忆合金，其密度为6000 kg/m3，马氏体状态的弹性模量为 20 GPa，泊松比为0.35；奥氏体状态的弹性模量为80 GPa，泊松比0.3；环氧树脂的弹性模量为 1 GPa，泊松比为0.43，密度为800 kg/m3。

图1 声子晶体 (灰色、深灰色和白色分别代表环氧树脂、形状记忆合金和真空)

3 分析模型

3.1 形状记忆合金(SMA)的相变规律

SMA在外部刺激(如加热和卸载)下可发生相变，实现材料性质的变化。在自由应力状态，高温下的形状记忆合金材料以母相奥氏体结构形式存在，当温度降低时，晶体结构发生相变，转变为马氏体相。本文考虑由温度诱发的低温孪晶马氏体相和高温奥氏体相之间材料性质的转变。马氏体的内部状态变量马氏体体积分数ξ，从初始阶段ξ0到低温T(Mf≤T≤Ms)的孪晶低温马氏体的过程可表示为

(1)

而在高温条件下(As≤T≤Af)，从马氏体相向奥氏体相的逆向转变则可表示为

(2)

式中ξ0为相变初始状态的马氏体体积分数。Ms和Mf为奥氏体向马氏体转变的开始和结束温度，As和Af为马氏体到奥氏体相变的开始和结束温度。本文采用NiTi形状记忆合金，其相变温度分别为Ms=295 K，Mf=291 K，As=308 K，Af=318 K。

SMA的弹性模量与马氏体分数有关，可表示为

E=EA+ξ(EM-EA)

(3)

式中EM和EA分别为全马氏体相和全奥氏体相的弹性模量。奥氏体的弹性模量EA大约是马氏体弹性模量EM的3倍。改变SMA的温度会改变其杨氏模量，并相应地改变带隙大小和位置。

3.2 声子晶体的带隙分析模型

二维弹性结构的面内模态的控制场方程可表示为

(4)

周期性弹性系统的位移场的形式为

u(r)=uk(r)exp(ik·r)

(5)

式中波矢量k=(kx,ky)为第一布里渊区(如图1(c)所示)的Bloch函数，uk为与单胞具有相同周期性的周期向量函数。

根据Bloch定理，有如下形式的Floquet周期条件

u(r+a)=u(r)exp(ik·a)

(6)

式中a为声子晶体的空间周期向量。

在单胞的边界施加布里渊区的Floquet周期边界条件，波矢k沿着M→Γ→X→M进行扫描，并采用有限元法对单胞进行离散，可获得色散方程的有限元列式为

(K-ω2M)U=0

(7)

式中U为节点处位移，K和M分别为与波矢k相对应的刚度矩阵和质量矩阵。

本文基于商用软件COMSOL建立有限元模型，并进行色散关系计算。由于结构的周期性，在计算中只需考虑一个单胞结构。通过扫描第一不可约布里渊区中的波向量，可以计算出特征频率，然后得到色散关系和本征模态。

4 结果与讨论

取晶格常数为L=0.03 m，矩形孔的长为a=0.015 m，宽为b=0.001 m。利用有限元法计算频率范围在0 kHz～110 kHz单胞的能带结构。当散射体边长为0.01 m时，声子晶体结构的能带结构如图2所示。当温度低于Ms时，散射体处于孪晶马氏体的稳定状态，在这个状态下打开了两条带隙，第一条带隙位于第12带和第13带之间，带隙起始频率在21.36 kHz～57.92 kHz内变化，带隙的宽度为36.56 kHz。第二条带隙出现在第44带和第45带之间，带隙起始频率在87.99 kHz～93.92 kHz 内变化，带隙的宽度为5.93 kHz；当升高温度至As时，孪晶马氏体不再处于稳定的状态，开始向奥氏体转变。当温度升高至Af时，形状记忆合金完全发生相变，孪晶马氏体完全转变为奥氏体。从马氏体变成奥氏体，弹性模量大约增加了 3倍。此时，能带图出现了四条带隙，如图2(b)所示。第一条带隙出现在第12带和第13带之间，带隙起始频率在21.96 kHz～66.35 kHz内变化，带隙的宽度为44.39 kHz。相比于散射体是马氏体的情况，第一带隙的上边界向高频偏移，下边界向低频偏移，带隙的宽度增加17.5%，带隙宽度明显拓宽，证明通过合理布置SMA的位置，可以实现带隙宽度的调控。第二条带隙出现在第20带和第21带之间，带隙起始频率范围为68.85 kHz～76.84 kHz，带隙的宽度为7.99 kHz。对比图2(a)，在这个频率范围内产生新的带隙，引入SMA在特定频率起到了开关作用，可以有效控制弹性波的传输。第三条带隙出现在第28带和第29带之间，带隙起始频率在81.56 kHz～103.28 kHz变化，带隙的宽度为21.72 kHz，对比于散射体是马氏体的第二条带隙，带隙宽度是其2.72倍。第四条带隙出现在第32带和第33带之间，频率范围为104.14 kHz～107.56 kHz，带隙的宽度为3.42 kHz，带隙宽度较窄。在SMA从马氏体向奥氏体相变后，带隙的宽度明显拓宽，而且在没有带隙的位置出现了新的带隙，在特定频率起到了开关的作用，带隙可调性是由于SMA在热激活作用下的相变及其随后的弹性模量变化造成的。验证了SMA的引入可实现声子晶体的带隙可调，为可调带隙的发展提供了新的机会。

为了清楚理解上述带隙产生的机制，本文列出图2能带结构对应的带隙上下边界的特征模态位移场(图3和图4)。散射体是马氏体的单胞的带隙上下边界的特征模态如图3所示，第一条带隙的下边界是周围的基体材料绕着中心散射体做顺时针旋转运动，带隙上边界是连接四个质量块的韧带在做剪切运动，但运动方向不同，致使竖向穿孔中间部分拉伸，横向穿孔中间部分压缩；第二条带隙的下边界是横向穿孔的周围材料做旋转运动，其他地方未有明显位移，带隙的上边界是基体材料沿着对角线方向运动，出现对角线对称的位移场。

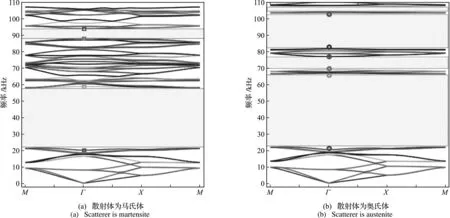
图2 能带结构

图3 散射体是马氏体时带隙上下边界处单胞的振动特征模态

散射体是奥氏体单胞的带隙上下边界特征模态位移场如图4所示，第一条带隙的下边界是周围材料绕着中心散射体做旋转运动，与散射体是马氏体的第一条带隙的下边界振动模式相同，上边界是连接四个质量块的韧带做剪切运动，不同的是竖向连接韧带剪切位移明显，横向连接韧带位移较小，这与散射体是马氏体的振动模式不同，与中间散射体的刚度增大有关；第二条带隙的下边界是连接韧带做剪切运动，竖向穿孔和横向穿孔的中间部分同时受压缩，带隙上边界横向穿孔和竖向穿孔中间的材料做旋转运动；第三条带隙下边界与第二条带隙上边界的振动模式相同，带隙上边界横向穿孔周围的材料做剪切运动。

图4 散射体是奥氏体时带隙上下边界处单胞的振动特征模态

为进一步分析SMA对声子晶体能带结构的影响，分析了散射体的填充分数对第一带隙的具体影响。如图5所示，随着散射体填充分数的增加，散射体是奥氏体和散射体是马氏体的带隙上下边界的变化趋势是相同的，带隙上边界先增加后减小。带隙下边界先减小后增大。但是，散射体是奥氏体的带隙上边界明显高于散射体是马氏体的带隙上边界的位置，下边界两者的位置比较接近。图5(b)是带隙宽度随着散射体填充分数增加的变化情况。散射体是奥氏体(黑色曲线)和散射体是马氏体(灰色曲线)的带隙宽度随着填充分数的增加，带隙宽度均呈现先增加后减小的趋势。特别注意，散射体是奥氏体的带隙宽度比散射体是马氏体更晚到达峰值。同时，散射体是奥氏体的带隙宽度明显高于散射体是马氏体的带隙宽度，进一步说明，引入SMA可以调控带隙的位置和宽度。

图5 带隙上下边界和宽度随着填充分数的变化

为了解弹性波在超材料板的动态响应，对 10×2个散射体为0.01 m的单胞组成的PCs进行了频域摄动分析，计算其透射谱，可由式(8)求得

T=20log|Aout|/|Ain|

(8)

式中Ain和Aout为输入和输出加速度信号。在上下边缘具有连续的周期性边界条件，周围设置完美匹配层以保证开放边界条件。另外，所设计的声子晶体具有XY方向的各向同性性质，两个方向的传播特性是相同的。声子晶体薄板内振动衰减非常明显，对应带隙频率段的波无法在薄板中通过，这个频率范围与带隙范围误差很小，可见声子晶体薄板在带隙范围内减振效果显著，其他频率段内的波都可以通过。散射体是马氏体如图6(a)所示，波衰减的频率范围与图2(a)带隙的位置吻合，散射体是奥氏体如图6(b)所示，有着更宽的衰减范围，同带隙频率段衰减更加明显，与图2(b)也是吻合的。为了进一步研究波在声子晶体薄板的传播行为，分别在薄板的左端施加68 kHz,50 kHz和 85 kHz 的激励。对于散射体是马氏体的情况如 图7(a，c，d)所示，68 kHz和85 kHz属于带隙外的频率，波可以在板中通过，50 kHz是属于带隙内的频率，波无法通过薄板；对于散射体是奥氏体的情况如图7(b，d，f)所示， 68 kHz属于带隙外的频率，波可以在板中通过，50 kHz和85 kHz属于带隙内的频率，波无法通过薄板。图7(e，f)中，波在板内传播的对比进一步证明了在声子晶体中引入SMA起到了开关的作用。

图7 声子晶体薄板透射谱的衰减

5 结 论

通过温度诱导SMA相变，SMA在低温孪晶马氏体和高温奥氏体相互转变，改变了材料的弹性模量大小。利用SMA这种材料特殊的性质，设计了一种SMA与传统材料环氧树脂结合的2D穿孔智能结构。通过合理布置缝隙与形状记忆合金相材料的位置，实现声子晶体带隙性质的可调设计。采用有限元法与Bloch理论计算微结构的特征频率的面内色散关系，该结构实现了带隙宽度可调控和在其他频率范围打开新的带隙。同时，研究表明第一带隙随着散射体(SMA)填充分数的增加，带隙宽度先增大后减小，奥氏体的带隙上边界明显高于马氏体的带隙上边界，但下边界两者比较接近。

参考文献(References):

[1] Kushwaha M S,Halevi P,Dobrzynski L,et al.Acoustic band structure of periodic elastic composites [J].PhysicalReviewLetters,1993,71(13):2022-2025.

[2] Sigalas M M,Economou E N.Attenuation of multiple-scattered sound [J].EurophysicsLetters(EPL),1996,36(4):241-246.

[3] Liu Z Y,Chan C T,Sheng P.Three-component elastic wave band-gap material [J].PhysicalReviewBCondensedMatter,2002,65(16):165116.

[4] Casadei F,Beck B S,Cunefare K A,et al.Vibration control of plates through hybrid configurations of periodic piezoelectric shunts [J].JournalofIntelligentMaterialSystemsandStructures,2012,23(10):1169-1177.

[5] Vasseur J O,Hladky-Hennion A C,Djafari-Rouhani B,et al.Waveguiding in two -dimensional piezoelectric phononic crystal plates[J].JournalofAppliedPhysics,2007,101(11):114904.

[6] Casadei F,Dozio L,Ruzzene M,et al.Periodic shunted arrays for the control of noise radiation in an enclosure[J].JournalofSoundandVibration,2010,329(18):3632-3646.

[7] Shi H Y Y,Tay T E,Lee H P.Numerical studies on composite meta-material structure for mid to low frequency elastic wave mitigation[J].CompositeStructures,2018,195:136-146.

[8] Li F M,Wang Y S.Study on wave localization in disordered periodic layered piezoelectric composite structures[J].InternationalJournalofSolidsandStructures,2005,42(24-25):6457-6474.

[9] Casadei F,Delpero T,Bergamini A,et al.Piezoelectric resonator arrays for tunable acoustic waveguides and metamaterials[J].JournalofAppliedPhysics,2012,112(6):064902.

[10] Wang P,Casadei F,Shan S,et al.Harnessing buckling to design tunable locally resonant acoustic metamate -rials[J].PhysicalReviewLetters,2014,113(1):014301.

[11] Xia B Z,Chen N,Xie L X,et al.Temperature -controlled tunable acoustic metamaterial with active band gap and negative bulk modulus[J].AppliedAcoustics,2016,112:1-9.

[12] Brinson L C,Bekker A,Hwang S.Deformation ofshape memory alloys due to thermo -induced transformation[J].JournalofIntelligentMaterialSystemsandStructures,1996,7(1):97-107.

[13] Ruzzene M,Baz A.Control of wave propagation in periodic composite rods using shape memory inserts[J].JournalofVibrationandAcoustics,2000,122(2):151-159.

[14] de Sousa V C,Tan D,De Marqui Jr C,et al.Tunable metamaterial beam with shape memory alloy resonators:Theory and experiment[J].AppliedPhysicsLetters,2018,113(14):143502.

[15] Lü X F,Xu S F,Huang Z L,et al.A shape memory alloy-based tunable phononic crystal beam attached with concentrated masses[J].PhysicsLettersA,2020,384(2):126056.

[16] Chuang K C,Lü X F,Wang Y H.A bandgap switchable elastic metamaterial using shape memory alloys[J].JournalofAppliedPhysics,2019,125(5):055101.

[17] Tian X Y,Chen W J,Gao R J,et al.Perforation-rotation based approach for band gap creation and enlargement in low porosity architected materials[J].CompositeStructures,2020,245:112331.

[18] Brinson L C.One -dimensional constitutive behavior of shape memory alloys:thermomechanical derivation with non-constant material functions and redefined martensite internal variable[J].JournalofIntelligentMaterialSystemsandStructures,1993,4(2):229-242.