二维结构中亚波长缺陷的超声特征

(苏州大学 轨道交通学院，苏州 215131)

常见的用于检测材料缺陷的无损检测方法有以下几种:超声检测(UT)、射线检测(RT)、渗透检测(PT)、磁粉检测(MT)和涡流检测(ET)等[1]。与其他无损检测方法相比，超声检测因具有检测对象范围广、检测深度大、灵敏度高、成本低、对人体无害等优点，而得以广泛应用[2]。在复合材料中，对于亚波长(即缺陷尺寸小于波长)缺陷的检测还比较困难[3]，尤其是当有两个或两个以上散射体同时存在时，这是因为两散射体间存在耦合效应，探测得到的反射回波中的特征信息与只有单个散射体时的特征信息有较大区别，因此，如何从得到的反射回波中提取有用的特征信息以确定两散射体的大小、距离以及排列角度就成为了需要解决的问题。

传统的超声检测技术通常会分析特征值，如声速、声衰减和声阻抗[4]。笔者主要研究铝板中干扰散射体对于需要重点检测的较大散射体的反射回波的影响，得到两散射体的尺寸及分布，为多缺陷损伤的检测提出了一些理论参考。为了实现这一目标，利用时域有限差分(Finite Difference Time Domain , FDTD)仿真软件计算了复合材料中声波的传播。FDTD方法通过离散化时间和空间来解弹性波方程，并通过运动方程中的有限差分代替导数[5-6]。 FDTD方法已广泛应用于电磁波传播的研究中[7-8]。

1 时域有限差分法仿真

时域有限差分法是电磁场计算领域的一种常用的数值解法，设一个含有空间和时间变量的分量F(x,z,t)，将其所在空间沿x轴、z轴离散化，分成多个网格单元，对其进行时域离散化，F(x,z,t)在时间和空间域中的离散值如式(1)所示。

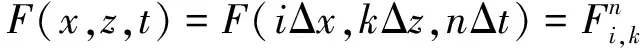
(1)

式中：Δt为时间步长增量；Δx和Δz分别为x轴和z轴方向的网格步长；i，k和n分别为空间步长和时间步长的个数。

求解有关F(x,z,t)的偏微分方程，用有限差分式表示F(z,t)对空间和时间变量的微分，采用二阶精度的中心差分近似，可得

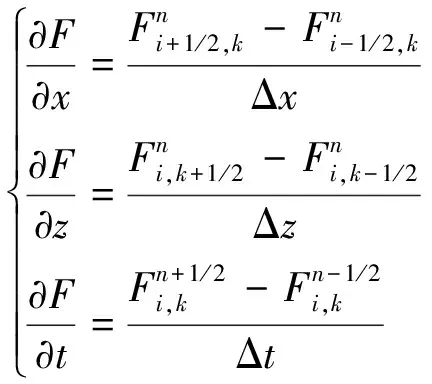
(2)

通过各离散点上的差商来近似替代函数在该点对时间和空间的偏导数，待求解的偏微分方程定解问题就转化为一组对应的差分方程的问题。

2 干扰项对主要散射体反射回波的影响

2.1 二维声学仿真模型

主要研究二维固-液结构，仿真模型示意如图1所示。模拟结构设置为边长50 mm的薄铝板，其中的散射体内部充满了水。为了保证有效的计算精度，x和y方向的网格精度设为0.02 mm，时间步长为2.22 ns。入射声源呈线性条状，长度为8 mm，排列于铝板左侧中心。在计算时，将温度设置为室温(25 ℃)，此时铝和水中的声速分别为6 325 m·s-1和1 500 m·s-1，这样在入射声波频率为1 MHz时，铝中声波的波长就是6.325 mm。接收器占一个网格，反射接收器位于铝板左侧1.6 mm处，透射接收器位于铝板最右端中心处，线状声源中心、反射接收器、透射接收器3者位于同一水平线上。整个仿真计算时间持续50 μs。仿真计算时，铝板四周设置完全匹配层(PML)[9-10]，为了达到最佳的吸收效果，匹配层厚度为入射波长的两倍。

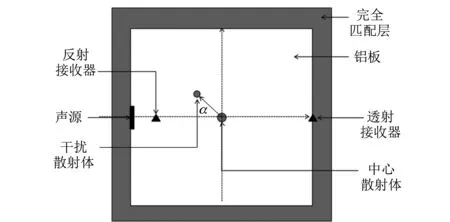
图1 二维固-液结构仿真模型示意

仿真计算时，设置铝板中心有一正圆形散射体，在其旁设置一个圆形干扰散射体，中心散射体与声源连线，以及中心散射体与干扰散射体连线形成的夹角α为两散射体的夹角，主要研究两散射体夹角α对于反射回波的影响。入射声源为正弦信号，其形式为

s(t)=sin(2πf0t)

(3)

式中：f0为超声声源频率；仿真计算时频率设为1 MHz。

声源持续时间为半个周期，即为500 ns，这时声源为正弦脉冲。文中主要对反射接收器接收到的反射信号进行处理分析。在研究过程中,选取中心散射体直径为1.265 mm，先将中心散射体与干扰散射体间距D(两圆形散射体外轮廓之间的距离)固定为1.265 mm，干扰散射体直径d依次为0.126 5，0.379 5，0.632 5，0.885 5 mm，研究两散射体角度及干扰散射体直径对于反射回波的影响；之后选取干扰散射体直径为0.632 5mm，改变两散射体的间距及角度，研究其对于反射回波的影响。因此，主要研究铝-水结构中干扰散射体对于中心散射体时域性的影响。

2.2 散射体参数对脉冲波的传播特性研究

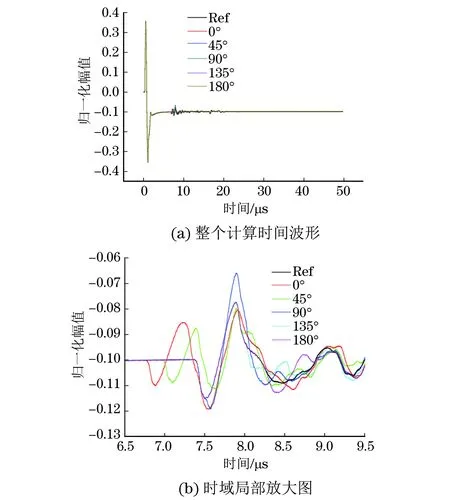
图2 干扰散射体直径为0.632 5 mm时，两散射体角度不同时的反射接收器接收波形

图2为干扰散射体直径为0.632 5 mm,两散射体角度不同时的反射接收器接收波形，图2中Ref信号为只有中心散射体，没有干扰散射体时的反射波形。由于反射接收器设置在入射声源与散射体之间，因此接收到的波形中的第一个正脉冲是入射波信号，之后的第二个负脉冲是反射回波信号。

图3为中心散射体直径为1.265 mm，两散射体间距为1.265 mm，干扰散射体直径依次为0.126 5，0.379 5，0.632 5，0.885 5 mm，两散射体呈不同角度时得到的反射波形。

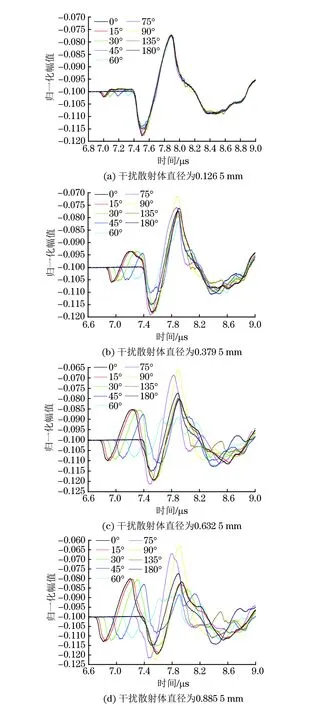
图3 干扰散射体直径与角度不同时反射信号时域局部放大图

当两散射体之间的角度小于60°时，反射波形呈现两组完整、明显，且较为独立可分辨的波峰及波谷，第一处波谷及波峰由干扰散射体的反射形成，且其峰值大小与干扰散射体的直径相关，而其出现的时间与两散射体的角度(干扰散射体与反射接收器距离)直接相关。当两散射体角度越小(即干扰散射体与反射接收器距离越小)，波谷及波峰出现得越早，波谷的时间可以用于推出干扰散射体的位置；而当两散射体角度越小，这个波谷及波峰就越完整，越易分辨：当两散射体呈0°时，波峰及波谷都十分明显且易辨别；而当两散射体呈60°时，只有第一处波谷较完整，并没有与之对应的完整波峰，且与第二处波谷没有较明显的界限。如果距离金属板表面距离H处有损伤，接收到负脉冲波与声源发射的时间间隔为t，铝板中声速为v，则缺陷的位置H可以由式(4)计算得出。

H=vt/2

(4)

求出两散射体的角度呈0°，干扰散射体不同直径时第一处波谷处的幅值，并与反射回波的归一化幅值(即-0.1)做差，得到结果如表1所示。

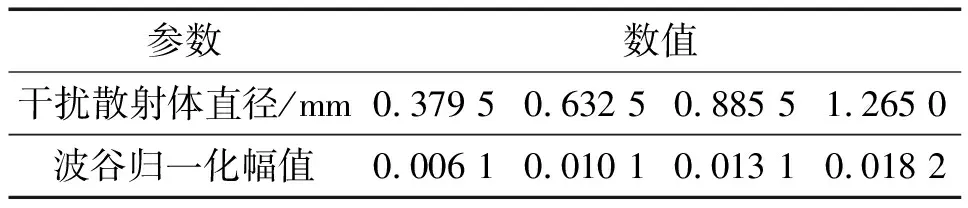
表1 两散射体呈0°干扰散射体时的不同直径反射回波波谷处幅值

发现干扰散射体直径比例为6∶10∶14∶20时，其波谷处幅值的比例也为6∶10∶13∶18，与干扰散射体直径的比例几乎相同，呈正相关，也就是说，当两散射体之间角度较小时(约小于60°)，即反射回波出现了两组明显可分辨的波谷及波峰时，可以通过第一组波谷的幅值求得干扰散射体的直径。

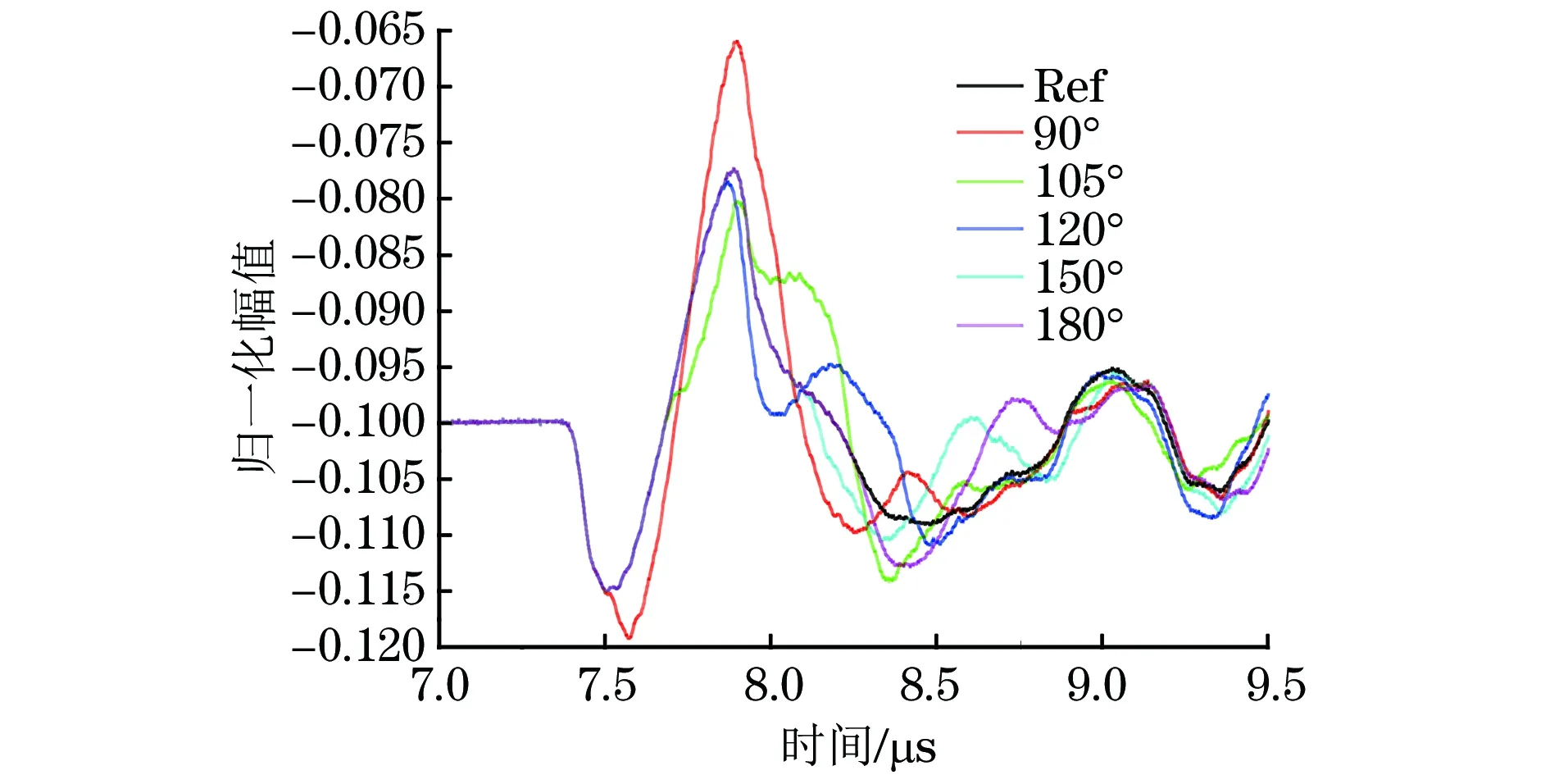
图4 两散射体角度不小于90°时的时域波形局部放大图

当干扰散射体与中心散射体呈90°时，反射回波的波峰峰值最大，且具有十分完整的波谷及波峰特征。干扰散射体直径为0.632 5mm，两散射体角度不小于90°时的反射回波波形的局部放大图如图4所示，图中Ref曲线为没有干扰散射体，只有中心散射体时的反射回波波形，发现当两散射体角度大于90°时，反射回波出现的第一个负脉冲波谷波形与没有干扰散射体时的负脉冲波谷波形重叠，在此波谷处的幅值均为0.015，即可通过此时波谷处的幅值确定中心散射体的直径。

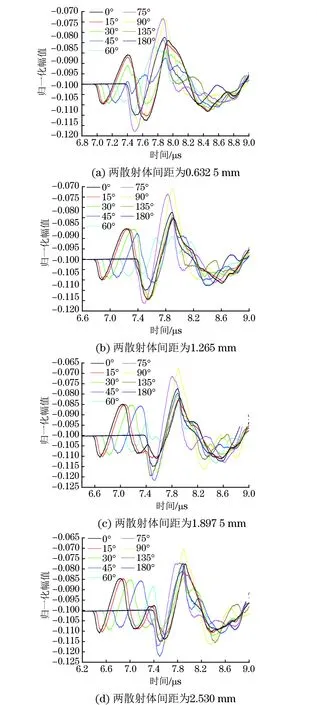
图5 干扰散射体距离与角度不同时反射回波时域局部的放大图

图5为中心散射体直径为1.265 mm，干扰散射体直径为0.632 5mm，两散射体间距依次为0.632 5，1.265，1.897 5，2.53 mm时，两散射体呈不同角度时得到的反射波形。发现随着两散射体间距的增加，在两散射体角度小于60°时，两组波谷以及波峰更易辨别，且第一处波峰与第二处波谷间的界限也更明显，这一现象在两散射体角度等于60°时最为突出：当两散射体间距较小时，并没有体现出完整的波峰及波谷特征；而当两散射体间距大于2.53 mm时，出现了完整的两组波谷以及波峰。显然可以通过第一处波谷的时间得到干扰散射体在铝板中的位置，也可以通过此波谷的幅值得到干扰散射体的直径。

3 试验过程

选用边长为50 mm的正方形薄铝板作为基础测试材料，铝板中打孔，在室温条件下将铝板放置于空气中进行测量，此时铝板中的微结构材料属性为空气。试验过程中选用RAM-5000/SNAP非线性高能超声测试系统平台，利用计算机采集数据，结合示波器观察探头的信号波形。

在铝板中心处钻取直径为1.265 mm的圆孔，并在其周围随机钻1个直径比其略小的圆孔。声源频率f取1 MHz。对铝板完成1次测量后，将铝板顺时针旋转90°再次测量，一共测量4次，得到波形如图6所示。

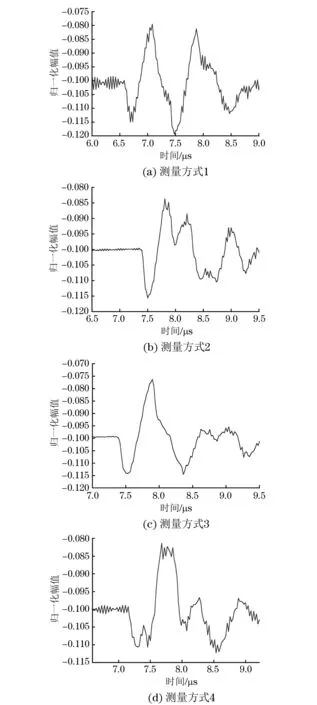
图6 不同测量方式下的反射回波局部放大图

从图6(a)的波形可以看出，此时反射回波出现两组十分明显且可分辨的波谷及波峰，判断此时两散射体角度小于60°，即-60°<α<60°，而此时归一化波谷幅值约为0.015，与前文对比，判断此时干扰散射体直径应约等于0.885 5 mm。而通过第一处波谷时间t1和第二处波谷时间t0的比值，在已知中心散射体圆心与铝板左侧距离H0的情况下，可求得干扰散射体圆心距铝板左侧距离H1=t1/t0×H0=22.3 mm。而测量方式3的波形图中只有1处十分明显的波谷及波峰，此时两散射体角度应在180°左右，可以通过此时的波谷求得中心散射体直径及位置。而测量方式4中的波形表现出了两散射体呈60°时特有的两小波谷之后伴随1个波峰的特征波形，判断此时两散射体角度应在±60°左右，此时角度是测量方式1顺时针旋转270°，结合对测量方式1的判断，则测量方式1中角度应接近30°。

通过对比4种测量方式获得的波形图，判断干扰散射体圆心应与铝板左侧水平距离为22.3 mm，干扰散射体直径约为0.885 5 mm，与中心散射体呈约30°。而实际干扰散射体直径为0.89 mm，与中心散射体呈25°，圆心与铝板左侧相距22.26 mm，这与通过波形得到的结果是十分相近的。

4 结语

利用时域有限差分法研究了具有亚波长微缺陷结构的铝-水结构的声波传播，提取散射体不同排列时反射回波的量化特征。为了突出缺陷对声信号的影响，与只有中心散射体的铝板反射回波进行对比。

研究表明，当两散射体间角度小于60°时，反射回波出现两组完整的波谷及波峰，此时可以通过第一处波谷的时间得到干扰散射体的位置信息，通过第一处波谷的幅值可以确定干扰散射体的直径范围；可以通过第二处波峰的时间得到中心散射体的位置信息，通过第二处波峰的峰值可以确定中心散射体的直径范围。

当两散射体角度为90°时，反射回波的波谷及波峰幅值最大。也就是说，在已知有两个散射体的情况下，从不同角度入射材料，当有一处获得最为明显且峰值最大的波谷及波峰波形时，两散射体间角度为90°。

而当两散射体间角度大于90°时，反射回波只有一处明显的波谷，且此波谷与没有干扰散射体时的波谷完全相同，此时可以通过波谷的时间及幅值直接得到中心散射体的位置及直径。若将待测件旋转检测，可以得到不同角度时的反射波形，则可以从不同角度反射波形图中分别提取特征值，以达到测量干扰散射体以及中心散射体的大小、位置、排列等参数的目的。