基于参数化水平集方法的微结构拓扑优化设计

魏 鹏,2， 范海坚， 李雪平*， 苏 成

(1.华南理工大学 土木与交通学院，亚热带建筑科学国家重点实验室，广州 510640；2. 华南理工大学 广东省高分子先进制造技术及装备重点实验室，广州 510640)

1 引 言

材料在微观尺度下可以看作是由众多拥有相似拓扑的微结构周期性排列而成的，且材料在宏观尺度下的属性不仅与材料本身的物理本质属性有关，还取决于材料内部微结构的拓扑[1]。为了获得微结构周期性排列的复合材料的性能，学者们通过均匀化方法来预测构成复合材料的周期性微结构的宏观等效属性[2]。通过逆向均匀化方法可以实现微结构的拓扑优化设计[3]，即以微结构的宏观等效属性为目标，通过迭代更新微结构内材料的分布状态，最终使材料在宏观尺度上表现出满足目标最优的性质。复合材料在物理性质、机械性能和热性能等方面具有单一材料不具备的优势，并在航空航天、汽车和机械等领域中得到了研究和应用。目前已有众多学者采用拓扑优化方法设计了刚度和热传导性最大化[4]、磁导率最大化[5]、流体渗透性最大化[6]和具有负热扩散系数[7]等性质的材料。

拓扑优化领域近几十年来在以程耿东等[8]为代表的学者做出的奠基性工作下不断发展进步。程耿东等[9]针对变厚度弹性薄板进行刚度优化设计，为连续体拓扑优化做出了先驱性工作。针对受到应力约束的结构拓扑优化问题，提出ε放松算法解决了应力奇异性问题。最近又提出了用序列整数规划方法求解拓扑优化问题[10]，为拓扑优化领域的发展作出了重要贡献。

本文拓扑优化模型采用的水平集方法最早由Osher等[11]提出，用于描述曲线和曲面的演化过程，应用于图像处理和计算机视觉等界面追踪领域。随后Sethian等[12]将水平集方法引入到结构拓扑优化研究中。水平集方法通过隐式模型描述结构演化边界，具有能够自动处理拓扑变化并获得清晰光滑边界的优势。传统水平集方法通过求解H-J(Hamilton-Jacobi)方程推动水平集函数点水平运动实现边界演化，这导致在求解过程中存在无法自动开孔和对初始设计依赖性高等问题。针对上述问题，学者们提出了半隐式格式的水平集方法[13]、分片常数水平集方法[14]、基于反应扩散方程的水平集方法[15]和参数化水平集方法[16]等，这些方法在一定程度上克服了传统水平集方法无法自动开孔的不足，但仍部分存在着数值不稳定及对初始设计依赖性高的问题。

本文采用参数化水平集方法，更新了水平集函数迭代格式，实现了自动开孔；结合水平集带方法，对零水平集附近的材料密度进行插值处理使其分布在[0,1]范围内,设计边界在优化过程中引入了中间密度以提高优化过程中的稳定性。并将上述方法应用于包括体积模量或剪切模量最大化和具有负泊松比性质的材料拓扑优化问题中，研究不同体积分数约束、多种初始设计及水平集带方法对优化结果的影响。

2 引入水平集带的参数化水平集方法

2.1 传统水平集方法

水平集方法核心思想是构建一个高一维的水平集函数，通过该水平集函数曲面与零平面的交线来表达材料分布区域的边界，如图1所示。其边界的定义可以表示为

图1 水平集函数(左)及对应的材料分布区域的边界(右)

(1)

传统水平集方法通过求解描述水平集函数演化方程，即下式的H-J偏微分方程来进行更新,

(2)

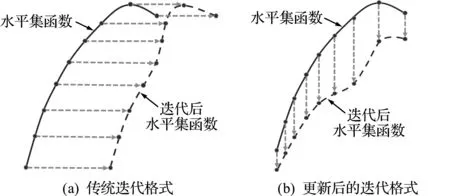
图2 更新前后的迭代格式

2.2 转换参数化水平集的迭代格式

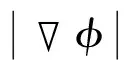
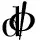
(3)

此时原来的H-J偏微分方程转换为更易求解的常微分方程，水平集函数的更新也仅取决于边界的法向速度Vn。如图2(b)所示，水平集函数的更新转换为各点的竖向运动，Vn的物理意义也变成了水平集函数点的竖向运动速度。

同时本文采用参数化水平集方法，引入基函数对水平集函数进行插值，将水平集函数转化为一系列基函数和相应参数的线性组合,

(4)

式中n为基函数数目，g(x)为基函数，α为对应的展开系数。基函数的选取可以根据需要选择为径向基函数、B样条函数和有限元形函数等[17]。本文采用MQ径向基函数，其形式为

(5)

式中xi为第i个节点的坐标，c为很小的常数。基函数仅与空间坐标相关，通过更新相应的参数α即可实现水平集函数的演化。由此可得到以α为设计变量的水平集函数迭代格式，

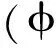
(6)

2.3 引入水平集带方法

水平集方法会严格地将边界两侧材料划分为{0,1}分布，在边界演化过程中会导致材料密度的突变，孔洞的生成消失都会造成数值的不稳定。而变密度法由于引入了中间密度，故在迭代演化中能够保持较好的连续性和稳定性。为了将变密度法中间密度的拓扑表现潜力引入水平集方法中，Wei等[18]提出了水平集带方法，故在零水平集附近的单元引入中间密度。即在原零水平集上下一定范围内引入密度插值函数，水平集带内的水平集函数值将会通过密度插值函数映射到指定的密度范围，表达式为

(7)

图3 水平集带方法

3 能量均匀化方法和拓扑优化模型

3.1 能量均匀化方法

一个宏观非均质的结构可以看作是由微观尺度上微结构单胞周期性重复组合构成，通过均匀化方法可以研究微观结构在周期性重复排列后的等效力学性能。

假设x为结构宏观尺度的全局变量，y=x/ε为材料微观尺度的局部变量，根据渐进展开理论，结构的宏观位移场uε(x,y)可以按参数ε展开为

uε(x,y)=ε0u0(x,y)+ε1u1(x,y)+

ε2u2(x,y)+…

(8)

(9)

(10)

(11)

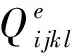
3.2 材料微结构拓扑优化设计模型

本文基于参数化水平集方法构建材料微结构的拓扑优化模型，将微结构的宏观等效特性作为拓扑优化的目标函数，

(12)

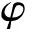
(13)

(14)

根据均匀化方法的等效弹性刚度矩阵定义，最大化材料体积模量的目标函数定义为

(15)

式中K为体积模量值。最大化材料剪切模量的目标函数定义为

(16)

式中G为剪切模量值。由于负泊松比材料的特殊性，以负泊松比为目标的材料设计更为复杂。根据泊松比的定义，泊松比的计算如下，

(17)

因此目标函数选取为刚度矩阵中各元素的组合[19]

(18)

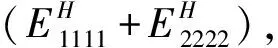
4 数值算例与结果分析

本节分别针对最大化体积模量、剪切模量和具有负泊松比的材料进行拓扑优化设计。其中实体材料和空材料的杨氏模量分别为1和1×10-9，泊松比均为0.3，有限元网格划分为50×50。

4.1 体积模量最大化

以体积模量最大化为目标函数，体积分数为0.5。水平集带初始带宽为3，每次迭代减小0.1，最终带宽收敛至0。图4是对应的水平集函数及水平集带。表1列出了不同迭代步下的微结构拓扑及其密度分布。图4在迭代开始时，零水平集上下存在着水平集带边界，边界内的水平集函数对应的单元密度在ε和1之间，如图1所示此时存在着许多中间密度单元。随着优化的进行，水平集带上下边界逐渐收缩至重合，中间密度单元逐渐消失，单元密度接近黑白分明的{ε,1}分布。

图4 水平集函数及水平集带的演化过程

表1 体积模量最大化优化过程

最终优化的微结构等效弹性刚度矩阵如下，体积模量值为0.190。

为了进一步验证所得体积模量的最优，在此引入复合材料设计的HS(Hashin-Shtrikman)边界[20]，该理论用于预测复合材料宏观等效特性的界限值，可表示为

(19)

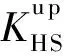
图5 优化结果与HS边界值对比

表2列出了在不同初始设计下，体积分数为0.5，是否引入水平集带方法的优化结果比较。在部分情况下，引入水平集带方法能获得更合理的优化结果。对于较为简单的体积模量最大化问题，迭代过程中拓扑变化较小，水平集带方法对优化结果的提升并不明显。

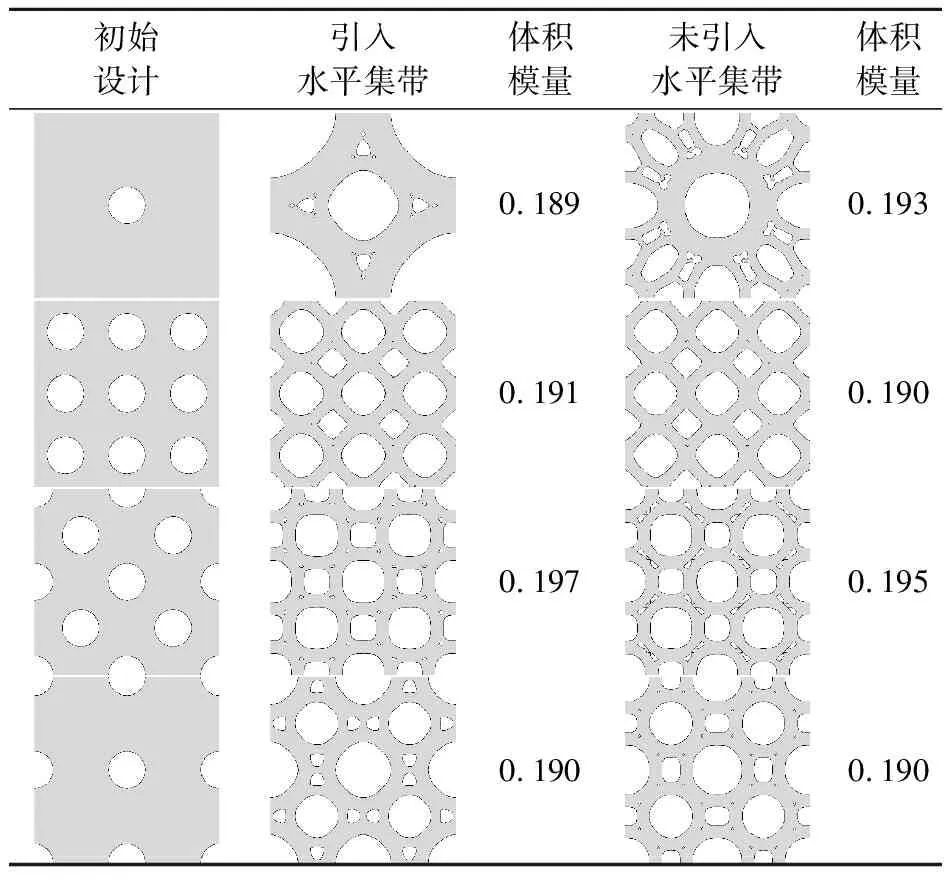
表2 不同初始设计的优化结果

最终的优化结果对于初始设计和优化参数都比较敏感，说明了材料设计问题具有较多的局部最优解，呈现明显的非凸性[3]。这是因为定义的目标函数式(15)同时与等效弹性矩阵的4项数值相关，同一目标函数值可能对应着4项数值不同的搭配，也对应着不同的等效弹性刚度矩阵和微结构拓扑，这也说明微结构拓扑与刚度矩阵并非一一对应的关系，从而导致具有众多局部最优解。

4.2 剪切模量最大化

以剪切模量最大化为目标函数，水平集带初始带宽为3，每次迭代减小0.1，最终收敛至0。表3列出了优化结果，包括各种初始设计和不同体积分数下(0.2,0.4,0.6)的微结构拓扑、3×3微结构分布及对应的剪切模量值G。以剪切模量最大化为目标的优化结果材料分布在45°斜对角线上，即与切应力平行的方向，说明材料得到了充分的利用。虽然不同初始设计下的微结构拓扑不完全相同，但其周期性排列的形式是基本相似的，也侧面说明了材料设计优化结果的非唯一性。因此虽然材料设计的优化结果很大程度上取决于初始设计和优化参数，但通过合理选择模型和方法仍可以获得较优的结果。

表3 不同初始设计和体积分数下的优化结果Tab.3 Optimal results under different initial designs and volume fraction

4.3 负泊松比材料

为了获得具有负泊松比性质的材料，以式(17)为目标函数，取体积分数为0.4，对各种初始设计，及是否引入水平集带方法进行对比。针对更为复杂的负泊松比问题，为了提高迭代稳定性[18]，在此处设置水平集带初始带宽为6，每次迭代减小0.05，最终带宽收敛至0。表4列出了4种初始设计下的负泊松比优化结果。负泊松比材料的获得说明了本文方法和模型的有效性，且与文献[21，22]有着相似的拓扑形式。横向对比发现对于拓扑变化较大的负泊松比问题，引入水平集带后能够促进负泊松比的获得，并且有着更小的泊松比。尤其是对于初始设计2，引入水平集带后能够避免求解陷入某些局部最优解，最终收敛于更合理的结果。

图6是表4初始设计2引入水平集带方法的迭代收敛曲线。在前30步为了满足体积分数约束，体积分数和目标函数迅速变化，结构拓扑发生显著变化，当满足体积约束后曲线趋于平稳并最终达到收敛条件，说明本节所采用的材料设计方法具有较高的优化效率。

表4 负泊松比优化结果Tab.4 Optimal results with negative Poisson’s ratio

为了展示及验证微结构的负泊松比特性，将上述算例的3×3分布形式导入ANSYS进行分析。该模型尺寸为150 mm×150 mm。对模型左右两端约束其竖向位移并分别施加向左向右的拉伸位移0.5 mm。结果如图7所示，黑色实线和灰色云图分别为变形前后结果。在左右施加拉伸位移后，上下两端均产生了向外膨胀的位移，说明了由该微结构周期排列形成的材料具有负泊松比的性质。取图7黑色虚线框内的单胞进行分析，其左右两侧平均位移为0.170 mm，上下平均位移为0.105 mm，计算泊松比约为-0.612，与算例结果-0.607相近，也说明了本文采用的能量均匀化方法的有效性。

图7 负泊松比仿真分析

5 结 论

本文采用了参数化水平集方法，更新了水平集迭代格式，并结合水平集带方法，以材料的体积模量、剪切模量最大化和负泊松比为目标进行了微结构拓扑优化设计。优化结果表明，(1) 更新了迭代格式和引入水平集带方法的参数化水平集方法具有较高的优化效率和稳定性，并且能得到清晰光滑的材料边界；(2) 本文方法能够根据目标函数有效地搜寻到满足特定性能的材料微结构；(3) 材料设计问题具有较多局部最优结果，最优的微结构拓扑不具有唯一性；(4) 水平集带方法对于拓扑变化较小的体积模量最大化问题的求解优势并不明显，但对于复杂的负泊松比材料设计问题，具有避免求解陷入局部最优解,从而获得更合理结果的优势。

本文方法能在一定程度上减轻优化结果对初始设计的依赖性，但并不能解决材料设计问题的非凸性。本文方法还可应用于最大化能量吸收问题和功能梯度材料的拓扑优化设计。

参考文献(References):

[1] Torquato S，Haslach H W.Random heterogeneous materials:Micro -structure and macroscopic properties[J].AppliedMechanicsReviews,2002,55(4):B62-B63.

[2] Guedes J,Kikuchi N.Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods[J].ComputerMethodsinAppliedMechanicsandEngineering,1990,83(2):143-198.

[3] Sigmund O.Materials with prescribed constitutive parameters:An inverse homogenization problem[J].InternationalJournalofSolidsandStructures,1994,31(17):2313-2329.

[4] Challis V J,Roberts A P,Wilkins A H.Design of three dimensional isotropic microstructures for maximized stiffness and conductivity[J].InternationalJournalofSolidsandStructures,2008,45(14-15):4130-4146.

[5] Guest J K,JH Prévost.Design of maximum permeability material structures[J].ComputerMethodsinAppliedMechanicsandEngineering,2007,196(4-6):1006-1017.

[6] Guest J K,Prévost J H .Optimizing multifunctional materials:Design of microstructures for maximized stiffness and fluid permeability[J].InternationalJournalofSolids&Structures,2006,43(22-23):7028-7047.

[7] Sigmund O,Torquato S.Design of materials with extreme thermal expansion using a three -phase topology optimization method [J].JournaloftheMechanicsandPhysicsofSolids,1997,45(6):1037-1067.

[8] Cheng K T,Olhoff N.An investigation concerning optimal design of solid elastic plates [J].InternationalJournalofSolidsandStructures,1981,17(3):305-323.

[9] Cheng G D,Guo X.ε -relaxed approach in structural topology optimization [J].StructuralOptimization,1997,13(4):258-266.

[10] Liang Y,Cheng G D.Further elaborations on topo -logy optimization via sequential integer programming and Canonical relaxation algorithm and 128-line MATLAB code [J].StructuralandMultidiscipli-naryOptimization,2019,61(1):411-431.

[11] Osher S,Sethian J A.Fronts propagating with cur-vature -dependent speed:Algorithms based on Hamilton-Jacobi formulations [J].JournalofComputationalPhysics,1988,79(1):12-49

[12] Sethian J A,Wiegmann A.Structural boundary design via level set and immersed interface methods [J].JournalofComputationalPhysics,2000,163(2):489-528.

[13] Luo J Z,Luo Z,Chen L P,et al.A semi-implicit level set method for structural shape and topology optimization[J].JournalofComputationalPhysics,2008,227(11):5561-5581.

[14] Wei P,Wang M Y.Piecewise constant level set me -thod for structural topology optimization[J].InternationalJournalforNumericalMethodsinEnginee-ring,2009,78(4):379-402

[15] Otomori M,Yamada T,Izui K,et al.Matlab code for a level set -based topology optimization method using a reaction diffusion equation[J].StructuralandMultidisciplinaryOptimization,2015,51(5):1159-1172.

[16] Wei P,Li Z Y,Li X P,et al.An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions[J].StructuralandMultidisciplinaryOptimization,2018,58(2):831-849.

[17] Wei P,Yang Y,Chen S K,et al.A study on basis functions of the parameterized level set method for topology optimization of continuums[J].JournalofMechanicalDesign,2020,143(4):1-48.

[18] Wei P,Wang W W,Yang Y,et al.Level set band method:A combination of density-based and level set methods for the topology optimization of continuums[J].FrontiersofMechanicalEngineering,2020,15(3):390-405.

[19] Xia L,Breitkopf P.Design of materials using topology optimization and energy-based homogenization app -roach in Matlab[J].StructuralandMultidiscipli-naryOptimization,2015,52(6):1229-1241.

[20] Hashin Z,Shtrikman S.A variational approach to the theory of the elastic behaviour of multiphase materials[J].JournaloftheMechanicsandPhysicsofSolids,1963,11(2):127-140.

[21] Amstutz S,Giusti S M,Novotny A A,et al.Topological derivative for multi-scale linear elasticity models applied to the synthesis of microstructures[J].InternationalJournalforNumericalMethodsinEngineering,2010,84(6):733-756.

[22] Wang Y Q,Luo Z,Zhang N,et al.Topological shape optimization of microstructural metamaterials using a level set method[J].ComputationalMaterialsScience,2014,87:178-186.