多子域模式重复结构多目标拓扑优化

王浩轩， 吴 开， 杜建镔

(清华大学 航天航空学院，北京 100084)

1 引 言

当今微电子和航空航天等高新工业领域的发展对结构的传热性能提出了更高的要求，电路的集成化和小型化使得热传导变得更加困难，如何对散热材料进行优化设计，从而利用有限材料获得更好的传热效果，对未来芯片的研究有重要的意义。在航空航天领域，高速飞行器伴随着严重的气动加热现象，如何设计同时满足力热要求的结构，也是一个值得研究的问题。拓扑优化是一种较为先进的优化方法，可以改变结构的拓扑构型，有很大的设计自由度，目前已广泛应用于力、热、声和振动等多种领域的优化当中。

工程中传热问题大多是连续体拓扑问题，对于连续体拓扑优化，早期最重要的开创性工作可追溯到20世纪80年代初Cheng等[1,2]针对板的优化设计研究。Bendsøe等[3]通过设计域内材料分布描述拓扑微结构，基于均匀化理论将微结构构型与宏观材料属性对应。但均匀化计算较为复杂，之后文献[4，5]发展了变密度拓扑优化方法，这种方法基于带罚因子的固体各向同性材料插值模型SIMP(Solid Isotropic Material with Penalty)，对中间密度的材料进行惩罚，使优化迭代趋于0～1分布，这种方法程序实现简单，优化效率高，应用范围较广。对于SIMP模型中的中间密度单元，Bendsøe等[6]给出了原因和物理解释。张君茹等[7]以SIMP法为基础，以二次型性能指标为目标函数，提出了实现旋转板减振设计的拓扑优化方法。牛飞等[8]以结构最小柔顺性为目标函数，提出了扩散结构优化设计的理论模型，并得到了二维和三维算例的合理结果。此外，进化结构优化方法、独立连续映射法ICM(Independent Continuous Mapping)和水平集方法等也有较为广泛的应用。

对于传热问题，左孔天等[9]基于SIMP材料插值模型，编制了传热结构的多目标优化算法，通过数值算例进行了验证。崔天福等[10]以密度法为基础，推导出了满足KKT(Karush-Kuhn-Tucker)条件的最优准则法迭代公式。龙凯等[11]基于ICM法，建立了周期性结构拓扑优化模型，针对不同循环周期下的算例进行计算和对比。魏啸等[12]基于密度法，分别以算数平均温度最小化、单位面积内能最小化以及平均温度梯度最小化为目标函数，对高导热材料分布形态进行了研究。Jing等[13]利用水平集法表示结构边界，采用网格生成法逼近热对流边界，验证了基于水平集的边界表达优化设计方法的有效性。Torii等[14]提出了一种具有多项式混沌展开PCE(Polynomial Chaos Expansion)的热传导鲁棒拓扑优化，给出了求解不确定大小、不确定位置的发热问题以及不确定位置的损伤问题的应用，证明了基于不确定性的优化方法能够获得更稳健的设计。Lohan等[15]利用生成算法对传热问题拓扑结构进行设计，表明生成算法相对于SIMP方法有更大的设计空间。

模式重复的思路来自于超材料的设计，超材料是一类人工复合材料或结构，其特点是具有周期性重复微结构。目前超材料的设计广泛使用拓扑优化方法，如Sigmund等[16]利用变密度法设计的负热膨胀系数超材料以及Christiansen等[17]设计的负折射率超材料。但目前大部分超材料设计均是材料级设计，即设计单胞尺寸远小于宏观尺寸。这种设计需要引入均匀化方法，且实际工程中限于制造精度，难以实现真正的材料级设计。而微结构尺寸与宏观尺寸相当的结构级微结构设计目前仅在仿生材料[18]领域有较广泛的应用，且单胞结构依赖于主观设计，受限严重。因此利用拓扑优化进行结构级超材料设计，在工程中是一个新的尝试。Liu等[19]讨论了一种基于对称性和模式重复的水平集拓扑优化方法，相较传统水平集方法减小了数值计算量，通过数值算例验证了方法的可行性和有效性。Wu等[20]提出了基于变量关联方法超材料柔性机构设计方法，获得了具有更高强健性的多胞柔性机构。

本文针对工程中的传热模式，以SIMP模型为基础，利用多子域不同分布来实现多种模式重复方案，对传热结构进行优化。现阶段传热领域大多以散热弱度为目标函数，本文考虑了工程中出现较多的局部温度优化问题，以局部温度最小化为优化目标进行设计。为了获得综合能力更强的结构，引入了多目标设计方法，对散热弱度和局部温度同时进行优化，避免了优化结果中的异常现象。同时考虑工程中的力热一体化问题，利用多目标方法，同时对结构散热弱度和静柔度进行优化。最后比较了模式重复结构和传统全域设计结构在缺陷影响下的性能。

2 理论模型与优化方法

2.1 模式重复设计模型建立

模式重复方法本质上是引入周期约束，将单个或多个设计域上的设计变量映射到全域上，目前研究较多的是单设计域映射方式，本文参考并发展了Wu等[20]提出的多设计域映射模型，并将其应用于热传导以及力-热一体化多目标优化问题。

考虑模式重复的单域设计和多子域设计概念模型如图1所示。将全域划分为大小相等的周期性单胞，单域模式重复的设计变量定义在其中一个单胞上；多子域模式重复的设计变量定义在其中多个单胞上，最后通过全等映射复制到其他单胞(由同种单胞映射而成的区域为一个子域)。

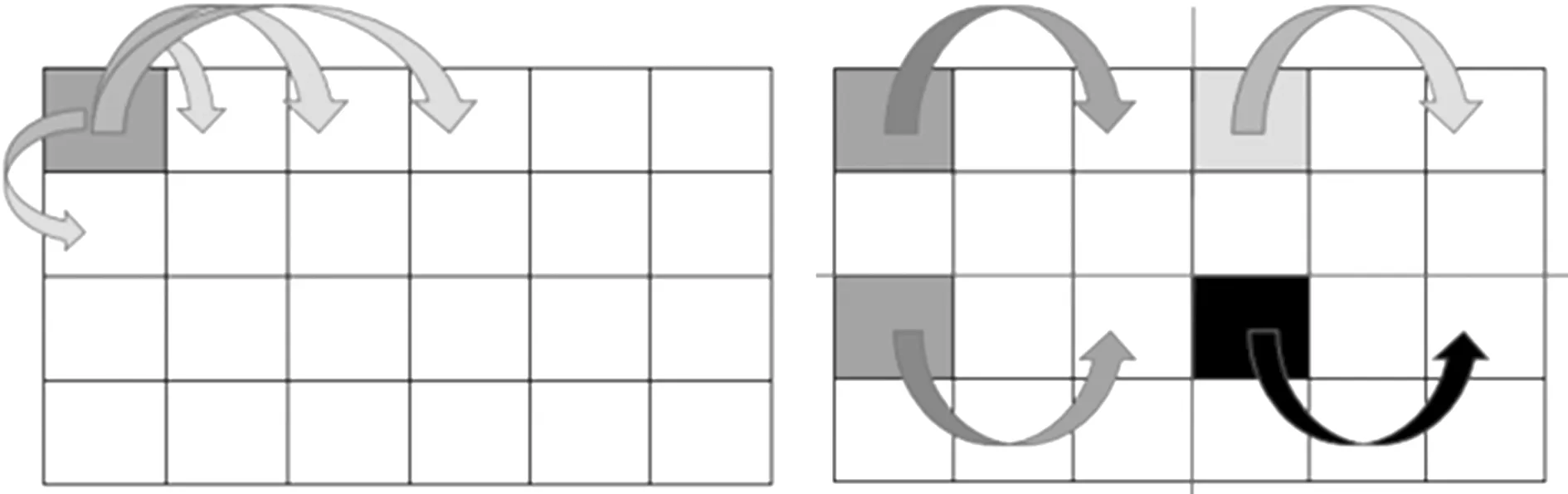
图1 考虑模式重复的单域和多子域设计的映射方式

首先以热传导拓扑优化问题为例，引入模式重复的拓扑优化模型可表示为

s.t.:KT=P

(1)

(2)

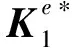
(3)

(4)

式中r为过滤区域的半径，α与迭代步数有关，可行的一种形式为α=max [1,(t-t0)]，t和t0分别为当前和迭代稳定时的迭代步数，目的是在迭代稳定后逐步减小过滤的影响。

2.2 最优条件与迭代求解

由拉格朗日乘子法易得式(1)的最优条件为

(i=1,…,n)

(5)

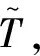
(6)

式中L为局部温度选择向量。由伴随法进行灵敏度分析，目标函数灵敏度可表示为

(7)

式中λ为目标函数增广拉格朗日函数的拉格朗日乘子。对于两种目标函数，λ可得

(8)

由于K只显含物理密度x，因此其对设计变量以链式求导法则进行灵敏度分析，可表示为

(9)

(10,11)

(12)

同样可以给出,

(13)

(i=1,…,n)

(14)

(15)

2.3 多目标优化模型和求解

多目标模型可利用加权方式将不同目标综合在一个目标函数当中，为保证优化中不同目标具有量级相近的变化率，可利用式(16)对散热弱度和局部温度进行加权处理[9]

(16)

s.t.:S=PTT

KT=P

(17)

此时目标函数灵敏度分析结果如下,

(18)

根据式(7，8)可求出。

3 问题与结果分析

3.1 均布内热源散热问题

考虑芯片散热的背景材料发热问题，全域尺寸为0.1 m×0.1 m，下边界中心有1/2长度的对流边界，其余边界绝热。两种设计材料导热系数分别为λ1=398 W/(m·K)，λ2=237 W/(m·K)，对应铜和铝，设定铜的体积约束为30%，这是双材料优化问题。对流边界换热系数h=2000 W/(m·K)，内部均匀热源Q=2.4×105W/(m2·K)，外部环境温度T∞=20 ℃，优化目标为散热弱度。

全域设计优化结果中，高导热材料(铜)基本都堆积在拓扑结构的下方，可以解释为整个区域的热量向此处集中，因此需要在此处铺设高导热材料以更高效地将热量导出。图2展示了全域设计、不同结构单胞数的单域设计和不同映射方案的多子域设计优化结果(不同方案Sx-y中，x为子域的个数，y为设计单胞的映射类型，具体分布如图8所示，不同颜色代表不同的子域)。可以看出，全域设计与模式重复设计之间，以及不同模式重复方案之间的拓扑结果有较大差异。这种差异产生的原因是模式重复方案引入了周期约束，而且不同映射方式也会影响优化效果。

图2 均匀内热源散热问题优化结果

为探究其中的联系，将不同映射方案和不同结构单胞数对应的拓扑结构下的散热弱度进行比较，如图3所示。横坐标表示每个方向上单胞的个数，纵坐标为对应优化结果的散热弱度。比较全域设计和模式重复可以看出，全域设计结果总是最优的，因为其具有最高的设计自由度；比较不同模式重复方案，此算例中多子域模式重复结果均优于单域模式重复结果，但并不是子域越多越好，与设计域映射方式有关。优化效果较好的三种方案为S2-2，S4-1和S4-3，具体分布如图2(c，d)所示。共同点是，(1) 材料整体处于结构下方，与全域设计相似； (2) 子域近似按照全域设计结构分区，保证了不同区域的不同需求。这对多子域模式重复的设计域映射方式有很好的借鉴作用。

图3 不同方案和单胞数的比较

3.2 恒定热流局部温度优化问题

以温度作为目标函数时，可以选择整个区域和局部区域甚至某几个点的温度进行优化，相较于散热弱度，可以针对特殊情况进行处理，如目标区域某个部分有耐热性差的材料，或是元件对温度较为敏感，则需要特别针对这部分进行局部优化。

全域模型如图4所示，发热元件位于全域上方，将其简化为恒定热流边界，长度为上边界尺寸的1/2，需通过设计散热通道将热量传导至下方对流边界。全域尺寸0.1 m×0.1 m,恒定热流q=20000 W/m，下边界为对流边界，其余边界绝热。两种设计材料导热系数分别为λ1=398 W/(m·K)，λ2=0.01 W/(m·K)，对应铜和空气，铜的体积约束为50%。对流边界换热系数h=2000 W/(m·K)，外部环境温度T∞=20 ℃。区域中央为一正方形保护区域，即需要进行局部温度优化的区域，占全域面积的1/4。

图4为全域设计优化结果，材料分为两部分，一部分分布在两边，将热流由上至下传至换热边界；另一部分在中央，将目标区域的热量导出。 这种结构的优势是保护区域温度极低，几乎等于环境温度，但不足之处是在热流入口处出现局部高温。

图4 简化模型和全域设计结果

由于优化目标和边界条件的特殊性，通过以下处理保证模式重复结果的合理性，令热流入口处单元密度恒为1，且不随迭代变化，可以保证热流能够进入区域，与实际工程也相符。利用多目标优化公式将散热弱度和保护区域温度联合，散热弱度为低权重，目的是防止非保护区域温度异常；保护区域温度为高权重，使保护区温度最小化。

不同模式重复拓扑结构如图5所示，相关参数列入表1。与问题1的相同点是模式重复结构优化效果均差于全域设计结果，而且温度相差较为明显，但此问题中全域设计结果在非保护区域出现明显高温，而这样的高温在工程应用中可能会受到很大限制。

图5 不同方案拓扑优化结果

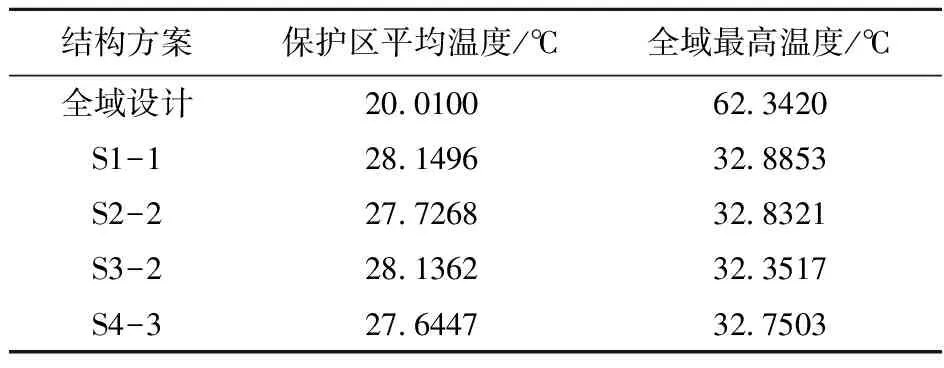
表1 不同方案参数

模式重复结构将热流边界与保护区域直接相连，这是模式重复结构与全域设计结构的最大不同之处。在模式重复中，即使考虑了将保护区域设为单独的子域(图5(b)左)，仍然无法避免这种直接相连的情况。这与模式重复方法本身的周期性约束有关，在这种约束下，模式重复方法对特定问题(如本节的局部温度优化)适应性较差。但是模式重复结构中，材料在全域内分布较均匀，这种结构更容易兼顾多种性能，对实际工程的复杂环境有较强的适应性。

3.3 力热一体化结构设计问题

力热一体化结构的优化设计可以对工程中复杂的力热一体化问题提出设计思路。本节基于简单的力热条件模型，探究模式重复在力热一体化结构设计中的可行性。

如图6所示，全域尺寸0.1 m×0.05 m，热边界条件为区域上边界中心有1/2长度的恒定热流边界，qh=20000 W/m，下边界为对流边界，换热系数h=2000 W/(m·K)，其余边界绝热，外部环境温度T∞=20 ℃。力边界条件，上边界中心有向下的集中力F=1000 N，下边界左右角为固定边界。设计材料为铝合金，体积约束30%。导热系数λ=160 W/(m·K)，弹性模量E=72 GPa，泊松比为0.33。热目标与力目标分别是散热弱度和静柔度，为多目标优化问题。

图6为简化模型以及不同力热权重下的全域设计结果，由于结构是左右对称的，方便起见只展示左半结构。可以看出，随两者权重的变化，拓扑结构逐渐从传力最优变化至传热最优。

图6 简化模型和全域设计结果(左半)

模式重复结构也有类似的变化，不同重复方案的结果如图7所示。当散热弱度与静柔度权重相当时，拓扑结构具有两者单独优化时的特征，可以看作是纯力优化与纯热优化的结合。不同方案下，模式重复方法均得到了清晰的结构。

图7 不同模式重复方案和不同权重组合结果(左半)

图8 不同多子域模式重复映射方案(不同颜色为不同子域)

4 结构在缺陷影响下的性能

分析全域设计结构和模式重复结构在受损状态下的性能。分析方式主要为全局分析，假设 0.1 m×0.1 m的结构上(如3.2节)出现了一小块缺陷，缺陷大小为0.0167 m×0.0333 m(结构1/6边长×1/3边长)，缺陷处材料设置为低性能材料。缺陷横纵坐标均进行变动，以遍历整个区域。每一组坐标为一个采样位置，记录此缺陷下结构的目标函数和全域最高温度等信息，得到一系列样本数据，进而对样本数据进行分析。以3.2节得到的最优结构为例，统计得到的样本数据标准差列入表2。

表2 恒定热流局部温度优化问题结构强健性分析

对恒定热流局部温度优化问题不同结构进行分析，发现不同结构中，全域设计的保护区平均温度和全域最高温度的标准差明显高于其他结构，说明全域设计结构在有缺陷影响时，性能波动较大，这是因为全域设计结构关键位置破坏后，热量会在上方集中，而模式重复结构由于每个单胞都有工作能力，因此不会存在这样的情况。则可以说明模式重复结构具有更强的抗缺陷能力。

5 结 论

本文通过两类传热结构设计,以及力热一体化结构设计，验证了多子域模式重复方法在热传导和力热一体化拓扑优化中的可行性。对以温度为目标函数的传热问题进行了分析，考察了多子域模式重复方法对局部优化问题的适应能力。最后比较了全域设计结构和模式重复结构在缺陷下的性能。

从优化效果看，模式重复设计与传统全域设计相比有较大差距，这主要是因为模式重复方法大大减小了设计自由度。但另一方面，模式重复有很多适合工程应用的特性和功能, (1) 模式重复结构由周期性微结构单胞排列而成，这为工程的模块化组装提供了基础，大大降低了制造难度。(2) 模式重复结构更擅长应对缺陷问题，即使局部失效，整体性能也不会受到太大影响。(3) 模式重复结构综合性能较为均衡，在多目标因素均衡设计中有很大应用空间。

多子域模式重复设计效果介于单域模式重复设计和传统全域设计之间，同时又继承了模式重复结构的诸多优点，因此是一种十分理想的模式重复方案。当然，多子域模式重复方法目前仍存在一定的不足。(1) 多子域模式重复中，子域的映射方案主要依靠经验和尝试，如参考全域设计结果和利用多子域均匀分布等，尚不能高效准确地进行最优映射。 (2) 多子域模式重复结构中存在结构冗余，这也是其性能相比全域设计有所降低的原因之一。 (3) 多子域模式重复方案对一些特定问题的适应性较差，实际应用中仍需根据具体需求选择全域设计或是模式重复设计。

参考文献(References):

[1] Cheng K T,Olhoff N.An investigation concerning optimal design of solid elastic plates [J].Interna-tionalJournalofSolidsandStructures,1981,17(3):305-323.

[2] Cheng K T,Olhoff N.Regularized formulation for optimal design of axisymmetric plates [J].InternationalJournalofSolidsandStructures,1982,18(2):153-169.

[3] Bendsøe M P,Kikuchi N.Generating optimal topolo -gies in structural design using a homogenization method[J].ComputerMethodsinAppliedMechanicsandEngineering,1988,71(2):197-224.

[4] Bendsøe M P.Optimal shape design as a material distribution problem[J].StructuralOptimization,1989,1(4):193-202.

[5] Rozvany G I N,Zhou M,Birker T.Generalized shape optimization without homogenization[J].StructuralOptimization,1992,4(3-4):250-252.

[6] Bendsøe M P,Sigmund O.Material interpolation schemes in topology optimization[J].ArchiveofApp-liedMechanics,1999,69(9-10):635-654.

[7] 张君茹,程耿东.基于二次型性能指标定轴转动板减振拓扑优化[J/OL].计算力学学报:1-8.[2021-07-26].http://kns.cnki.net/kcms/detail/21.1373.O3.20210408.1649.018.html.(ZHANG Jun-ru,CHENG Geng-dong.Topology optimization of vibration reduction of in-plane rotating plate around a fixed hub based on quadratic performance index[J/OL].ChineseJournalofComputationalMechanics:1-8.[2021-07-26].http://kns.cnki.net/kcms/detail/21.1373.O3.20210408.1649.018.html.(in Chinese))

[8] 牛 飞,王 博,程耿东.基于拓扑优化技术的集中力扩散结构设计[J].力学学报,2012,44(3):528-536.(NIU Fei,WANG Bo,CHENG Geng-dong.Optimum topology design of structural part for concentration force transmission[J].ChineseJournalofTheoreticalandAppliedMechanics,2012,44(3):528-536.(in Chinese))

[9] 左孔天,赵雨东,陈立平.传热结构的多目标拓扑优化设计研究[J].计算力学学报,2007,24(5):620-627.(ZUO Kong-tian,ZHAO Yu-dong,CHEN Li-ping.Study on multiple objective topology optimization of thermal conductive structure[J].ChineseJournalofComputationalMechanics,2007,24(5):620-627.(in Chinese))

[10] 崔天福,丁晓红,侯丽园.基于密度法的传热结构拓扑优化设计[J].上海理工大学学报,2014,36(6):548-555.(CUI Tian-fu,DING Xiao -hong,HOU Li-yuan.Structural topology optimization design of heat transfer based on density method[J].JournalofUniversityofShanghaiforScienceandTechnology,2014,36(6):548-555.(in Chinese))

[11] 龙 凯,贾 娇.基于ICM法的传热结构周期性拓扑优化设计[J].工程力学,2015,32(5):227-235.(LONG Kai,JIA Jiao.Periodic topology optimization design for thermal conductive structure using ICM method[J].EngineeringMechanics,2015,32(5):227-235.(in Chinese))

[12] 魏 啸,丁晓红.不同目标函数的传热结构拓扑优化研究[J].电子科技,2017,30(2):156-160.(WEI Xiao,DING Xiao -hong.Topology optimization of transfer structure for different objective functions[J].ElectronicScienceandTechnology,2017,30(2):156-160.(in Chinese))

[13] Jing G X,Isakari H,Matsumoto T,et al.Level set-based topology optimization for 2D heat conduction problems using BEM with objective function defined on design-dependent boundary with heat transfer boundary condition[J].EngineeringAnalysiswithBoundaryElements,2015,61:61-70.

[14] Torii A J,Santos D P D S,Medeiros E M.Robust to -pology optimization for heat conduction with polynomial chaos expansion[J].JournaloftheBrazilianSocietyofMechanicalSciencesandEngineering,2020,42(6):1-13.

[15] Lohan D J,Dede E M,Allison J T.Topology optimization for heat conduction using generative design algorithms[J].StructuralandMultidisciplinaryOptimization,2017,55(3):1063-1077.

[16] Sigmund O,Torquato S.Composites with extremal thermal expansion coefficients[J].AppliedPhysicsLetters,1996,69(21):3203-3205.

[17] Christiansen R E,Sigmund O.Designing meta material slabs exhibiting negative refraction using topology optimization[J].StructuralandMultidisciplinaryOptimization,2016,54(3):469-482.

[18] Ma Q,Cheng H Y,Jang K I,et al.A nonlinear mechanics model of bio-inspired hierarchical lattice materials consisting of horseshoe microstructures[J].JournaloftheMechanicsandPhy-sicsofSolids,2016,90:179-202.

[19] Liu Y,Li Z Y,Wei P,et al.Parameterized level-set based topology optimization method considering symmetry and pattern repe -tition constraints[J].ComputerMethodsinAppliedMechanicsandEngineering,2018,340:1079-1101.

[20] Wu K,Sigmund O,Du J B.Design of metamaterial me -chanisms using robust topology optimization and variable linking scheme[J].StructuralandMultidisciplinaryOptimization,2021,63:1975-1988.

[21] 杜建镔.结构优化及其在振动和声学设计中的应用[M].北京：清华大学出版社,2015.(DU Jian-bin.StructuralOptimizationandItsApplicationinVibrationandAcousticDesign[M].Beijing:Tsinghua University Press,2015.(in Chinese))