密度泛函理论计算半导体材料的带隙误差研究
2021-11-10张泽群孙庆德
张泽群,孙庆德
(中国工程物理研究院 a. 北京计算科学研究中心,b. 研究生院,北京 100193)
电子能带结构是材料最为关键的基本性质之一。从电子的能带结构出发,根据电子的填充情况,可以区分导体、半导体和绝缘体。带隙是半导体的电子能带结构中最为重要的性质之一,定义为导带的最小值(conduction band minimum,CBM)与价带的最大值(valence band maximum, VBM)之间的差值,可以根据CBM和VBM对应的高对称点是否相同分为直接带隙与间接带隙。能否较好地描述电子能带结构是第一性原理计算研究领域的一项重要研究课题。
对于材料电子能带结构的第一性原理描述,最常用的方法是基于局域密度近似(local density approximation, LDA)或广义梯度近似(generalized gradient approximation, GGA)的Kohn-Sham密度泛函理论[1-3],但是这个方法的不足是带隙的计算值偏小。对于传统的半导体材料,通过LDA或GGA法计算得到的带隙值均要比实验值小很多[4],且有材料的带隙越小,计算带隙误差越小的趋势,因此有观点认为当带隙为0时,就会像金属材料一样,LDA或GGA方法计算的带隙误差会消失。针对上述观点,本文中以半导体材料砷化镓为例,对LDA或GGA法带隙计算值的误差问题进行研究,并在理论上给出出现带隙误差的物理解释。
1 LDA或GGA法计算的带隙误差
LDA或GGA法可以在花费较少的计算资源的条件下得到材料体系较为准确的多种性质,但是这2种方法的主要缺点是会导致砷化镓、单晶硅等传统半导体的带隙计算值显著偏小。杂化泛函法是在LDA、GGA法的基础上引入Hartree-Fock交换能而得到的一种计算方法,例如Heyd-Scuseria-Ernzerhof(HSE)方法,可以更精确地计算带隙,但是相应的计算量和计算时长增加数倍。
采用不同方法得到的几种常见半导体材料的带隙计算值与实验值如表1所示。可以看出,LDA、GGA法计算得到的带隙的差别不明显,均存在带隙计算值偏小的现象,而HSE法计算得到的带隙与实验值较吻合,因此可以分别使用GGA、HSE法计算的带隙值代表LDA、GGA法的计算值和实验值。

表1 采用不同方法得到的不同材料的带隙计算值与实验值
对带隙误差进行进一步的分析,得到GGA法的带隙误差与带隙实验值之间的关系,如图1所示。由图可以看出,LDA、GGA法计算带隙的误差与材料本身的带隙具有正相关的趋势,即材料的带隙越大,则LDA、GGA法计算的带隙误差也越大;带隙越小,则LDA、GGA法计算的带隙误差也越小。对于金属材料来说,LDA、GGA法计算得到的结果是正确的,因此有观点认为,当半导体材料的带隙为0时,就会像没有带隙的金属材料一样,LDA或GGA法计算的带隙误差也会消失。

图1 采用广义梯度近似方法计算得到的 不同半导体材料的带隙误差与带隙实验值
本文中以闪锌矿构型(zincblende)的砷化镓为例,通过对其进行加压即压缩晶格体积的方式来减小带隙,分别利用GGA、HSE法进行计算,探究砷化镓的带隙为0时,LDA、GGA法计算的带隙误差是否消失。
2 计算方法
本文中所有的计算采用的是基于密度泛函理论的Vienna从头计算模拟软件包(Viennaabinitiosimulation package,VASP)[10]。在计算中使用了投影缀加平面波的方法来处理价电子与原子核之间的相互作用力[11]。体系的交换关联泛函采用基于GGA的Perdew-Burke-Ernzerhof 交互关联泛函(PBE)[12]法与杂化泛函HSE[13]法。对于所有的计算过程,设定平面波函数动能的截断能为500 eV; 在结构驰豫的过程中,设定原子受力与能量的收敛判据分别为0.1 eV/nm和10-5eV。简约布里渊区取尺寸为12×12×12(倒格矢a、b、c方向上高对称点K点的数量)的K点网格。在使用HSE法时,设定引入Hartree-Fock精确交换能的比例系数为0.28。
3 结果与讨论
通过对砷化镓晶格进行应变工程来调控体系的带隙,即通过施加外压压缩晶格体积的方式调控带隙。在具体的计算过程中,采取等比例改变VASP的输入文件POSCAR中基矢的缩放系数来实现,即从三维方向上同时等比例地压缩晶格常数,相当于改变了原胞的体积。确定基矢的缩放系数取值区间为0.80~1.06、步长为0.01进行计算,与平衡状态下的原胞相比,砷化镓晶格的体积变化率为51.2%~119.1%。
对于所得计算数据,通过拟合Birch-Murnaghan(BM)固体状态方程[14],可以分别获得砷化镓晶体的体系总能量、压强、体积弹性模量与晶格体积的关系,如图2所示。BM固体状态方程为
(1)
(2)
(3)
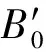

(a)总能量-晶格体积(b)压强-晶格体积(c)体积弹性模量-晶格体积GGA-PBE—基于广义梯度近似-Perdew-Burke-Ernzerhof 法; HSE—杂化泛函Heyd-Scuseria-Ernzerhof法。图2 采用不同方法计算得到的砷化镓晶体的体系总能量、压强、体积弹性模量与晶格体积的关系
利用GGA-PBE、HSE法分别计算得到的晶格常数、带隙等计算值与实验值如表2所示。可以看出,GGA-PBE法计算得到的晶格常数偏大,而带隙和体积弹性模量的计算值显著偏小; HSE法的计算值与实验值吻合较好。为了排除晶格常数的误差对GGA-PBE法计算带隙的影响,代入晶格常数实验值,分别采用GGA-PBE、HSE法进行计算,发现GGA-PBE法计算得到的体积弹性模量与HSE法的相同,而带隙计算值仍然偏小,说明晶格常数的差异不是引起带隙误差的主要原因。
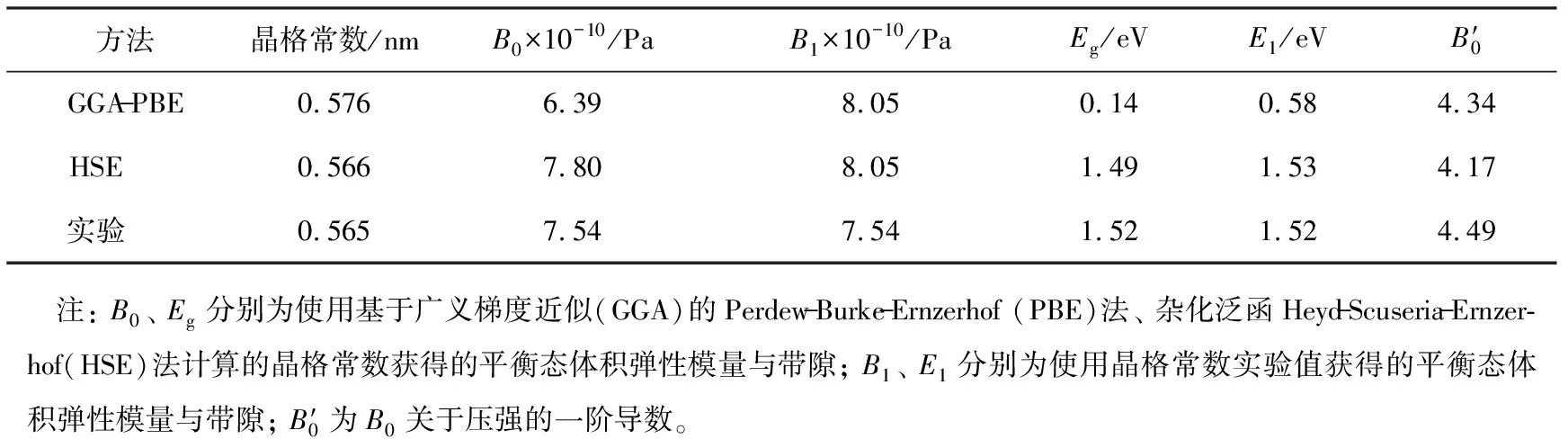
表2 采用不同方法得到的砷化镓晶格常数、体积弹性模量、带隙的计算值与实验值
在压缩晶格体积的过程中采用GGA-PBE、HSE法计算得到的砷化镓带隙与晶格体积、压强的关系如图3所示,其中的红色标点为平衡态的取值点。由图可以看出,2种方法计算得到的带隙均随着晶格体积的压缩经历一个先增大后减小的过程,且会产生由直接带隙半导体到间接带隙半导体的转换过程。
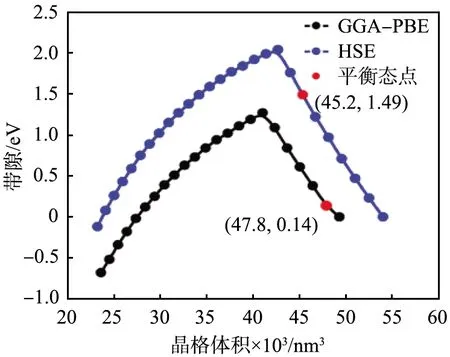
(a)晶格体积

(b)压强 GGA-PBE—基于广义梯度近似的Perdew-Burke-Ernzerhof 法;HSE—杂化泛函Heyd-Scuseria-Ernzerhof法。图3 不同方法计算得到的砷化镓带隙与 晶格体积、压强的关系
对砷化镓转为间接带隙半导体的过程进行研究,在这一过程中,价带最小值的取值点一直都在Γ点。选取砷化镓电子结构的高对称点Γ、X处的导带能量值随体积变化的关系进行研究,导带最小值的取值点会随着体积的压缩从Γ点转变到X点,由此产生了直接带隙半导体到间接带隙半导体的转变。计算得到的砷化镓导带的Γ、X点与价带Γ点之间的能量差值与晶格体积的关系如图4所示,图中标点处为对应2种方法的平衡态的取值点。

GGA-PBE—基于广义梯度近似的Perdew-Burke-Ernzerhof 法;HSE—杂化泛函Heyd-Scuseria-Ernzerhof法。图4 不同方法对应导带的Γ、X点与价带Γ点 之间的能量差值与晶格体积的关系
GGA-PBE、HSE法均显示,随着体积的压缩,Γ点能量不断增大; 随着体积的压缩,X点能量不断减小,其原因是对于砷化镓而言,Γ点的形变势是正的,而X点的形变势是负的。
对于间接带隙减小过程,HSE法计算的带隙误差、GGA-PBE法计算的带隙误差与带隙的关系如图5所示。由图可以看出,对于砷化镓而言,带隙越小,LDA或GGA法计算的带隙误差越小。

图5 采用基于广义梯度近似的Perdew-Burke-Ernzerhof 法计算的砷化镓的带隙误差与带隙的关系
进一步研究当半导体带隙减小到0时,不同方法计算的带隙误差是否会消失。根据图3,当采用GGA-PBE法,且晶格体积压缩到27.36×10-3nm3时(对应的压强为122 GPa),LDA或GGA法计算的带隙为0。当采用HSE法,体积压缩到23.58×10-3nm3时(对应的压强为190 GPa),带隙为0。两者对比可以看出,当压缩晶格体积使HSE法的计算的带隙为0时,GGA法计算得到的带隙并不等于0,反之亦然,因此当带隙为0时,LDA或GGA法计算的带隙误差会消失这一说法是不准确的。
为了探究引起带隙误差的根源,通过HSE法计算得到砷化镓在CBM、VBM处的波函数分布,如图6所示。由图可以看出,砷化镓的VBM主要是由砷原子(As) 的p轨道组成的,而CBM主要是由镓原子(Ga)的 s轨道组成的,这2个态的交换关联势之间存在差别,轨道波函数的不连续性是导致LDA、GGA法计算的带隙偏小的主要原因。

图6 砷化镓的导带的最小值与价带的最大值处波函数的分布
对砷化镓带隙形成的物理过程进行理论分析,如图7所示。VBM由As的p轨道和Ga的p轨道耦合得到,而CBM是由As的s轨道与Ga的s轨道耦合得到的,这种CBM与VBM处的s、p轨道波函数的不连续性与带隙关系不大,因此GGA的计算带隙误差也与带隙关系不大,即使带隙为0,这个误差仍然存在,这主要是由CBM和VBM的原子轨道组成决定的。

图7 砷化镓带隙形成的物理过程
4 结论
针对LDA、GGA法导致带隙计算值偏小的现象,本文中以砷化镓为例研究计算带隙误差与带隙的关系。结果表明,带隙趋近于0时,LDA、GGA法计算的带隙误差逐渐减小,但是并不会消失。对于GaAs半导体来说,CBM和VBM处的波函数的不连续性是导致LDA、GGA法计算带隙偏小的主要原因,而且这个计算误差不会随带隙的消失而消失,因此需要研究一种新的方法来对半导体的带隙进行更精准的计算,例如采用多体格林函数方法。
