人工智能在结构拓扑优化领域的现状与未来趋势

耿东岭 阎 琨 牛 斌

(1.大连理工大学 工业装备结构分析国家重点实验室，工程力学系，大连 116024； 2.大连理工大学 化工学院，大连 116024； 3.大连理工大学 机械工程学院，大连 116024)

1 引 言

结构拓扑优化旨在寻求材料的最优分布方式(结构拓扑)，使得在给定约束下，达到结构的某种性能要求，是公认的最具挑战的结构优化方法。在过去的三十年中，关于结构拓扑优化的理论成果及相关算法快速发展，不仅应用于机械、汽车、航空航天和海洋等工程制造领域，还应用于具有特定力学或电磁性能的微观材料的设计[1]。

关于结构拓扑优化问题的研究最早可追溯到20世纪初，Michell[2]利用解析法实现了桁架类离散结构在特定载荷和边界条件下的结构设计，相关算法称为Michell准则。程耿东等[3]在对实心弹性板最优设计的过程中创新性地指出其最优设计是由无限细的密肋增强结构构成。这项工作认为是近代拓扑优化的先驱。受到这项工作的启发，Bendsøe等[4]提出了均匀化方法，即将宏观结构的拓扑优化问题转化为材料微结构的尺寸优化问题。这一里程碑式的贡献促使更多的学者投入到均匀化方法相关的拓扑优化设计研究中。为了提高拓扑优化的计算效率，学者们提出了固体各向同性材料惩罚SIMP(Solid Isotropic Material with Penalization)方法[5-7]，该方法通过引入假设的可变密度材料，以单元的密度作为设计变量进行拓扑优化设计。与均匀化方法相比，SIMP方法执行更方便，能够便捷地完成拓扑优化过程。Xie等[8]提出了渐进结构优化ESO(Evolutionary Structural Optimization)方法，该方法的主要特点是移除应力较低区域的材料，从而实现结构的拓扑优化。上述这些方法称为基于密度的拓扑优化方法。与之相对的方法，称为基于边界演化的拓扑优化方法。该方法通过边界演化控制结构边界的变形来实现结构的拓扑优化，目前较为成熟的边界演化拓扑优化方法主要包括水平集法和可移动变形组件孔洞法。其中水平集(Level-set)方法[9,10]通过引入水平集函数的等值面来描述结构的边界，引入特定的速度场，通过函数的演化来获得下一时刻结构的边界形状。然而，水平集方法存在隐式表达结构边界的问题，对此Guo等[11-13]提出了可移动变形组件法MMC(Moving Morphable Components)和可移动变形孔洞法MMV(Moving Morphable Void)，该方法以一系列可以移动变形的显式组件或孔洞作为拓扑优化的基本模块，通过组件间的移动、交叠和覆盖，以及孔洞间的相互融合来实现结构的拓扑变化。除上述拓扑优化方法外，还包括独立连续映射ICM(Independent,Continuous,Mapping)法[14]、相场法[15-17]、拓扑导数法[18,19]、有限圆FCM(Finite Circle Method)法[20]以及基于智能优化算法的拓扑优化方法[21-24]等。

上述拓扑优化方法，特别是对于结构刚度优化问题其优化过程大体上可以分为结果拓扑轮廓初步成形阶段和材料细化分布阶段。拓扑轮廓初步成形阶段，材料由初始布局快速分布到给定载荷和边界附近，形成初步(模型轮廓模糊)的拓扑构型，这一过程中优化目标函数往往快速下降；而材料细化阶段在上一阶段获得的基本拓扑构型的基础上，逐渐细化材料分布，直到收敛于最优的拓扑(清晰)构型，优化目标函数在这一阶段呈现微调的变化特征。对于大规模的拓扑优化问题，完成结构的拓扑优化需要进行数百次甚至数千次的迭代过程，尤其是材料细化分布阶段，大量的迭代只是逐渐细化结构的局部构型，而整体的拓扑构型并没有发生较大的变化。然而，每一次迭代均需要进行同等大规模的有限元计算，不仅降低了计算效率，也越来越不能满足当今工业领域对于高效优质的设计需求，因此提高计算效率是目前拓扑优化领域亟待解决的主要问题之一。近年来，学者们陆续提出了一些改进拓扑优化计算效率的算法。Liu等[25]提出各向异性多孔介质宏微观材料/结构一体化优化的PAMP(Porous Anisotropic Material with Penalization)框架，相比于传统的层级优化方法，降低了设计变量的数目，提高了优化结果的可制造性。此框架成功应用到热弹性结构拓扑优化[26]和动力学频率拓扑优化[27,28]等问题。Kim等[29]将高分辨率拓扑优化拆分成从低分辨率到高分辨率多个阶段，提出了多尺度拓扑优化方法。Jang等[30]提出了一种基于固定网格在拓扑优化的同时对设计空间进行优化的方法。Aage等[31]基于C++并行计算库PETSc，提出了一套基于CPU并行的拓扑优化方法，并将其应用于大规模结构拓扑优化[32]。虽然上述研究成果显著提升了拓扑优化方法求解问题的计算效率和规模，但往往受限于拓扑优化迭代式求解的计算性质，仅对拓扑优化流程中结构有限元求解部分进行了加速，使得拓扑优化方法整体效率的提升仍受到一定限制。

随着计算机技术的迅猛发展和数据量的剧增，促使了以深度学习[33]为代表的机器学习算法[34]的空前发展，其相关的研究成果已经在计算机、金融、生命科学及传统工业等诸多领域得到广泛应用[35-38]。由于机器学习算法的特点为仅在离线训练阶段需要较高的计算成本，而在线使用过程不需要复杂的计算，常用于实现复杂计算过程的加速或实时计算。如通过训练完成的卷积神经网络CNN(Convolutional Neural Networks)模型[39]，实现对空气动力学领域相关的设计、分析和优化等问题的加速，提供及时的设计反馈[40]。基于条件生成对抗网络cGAN(conditional Generative Adversarial Networks)模型[41]，实现了在未知基本控制方程前提下，快速地对具有传导现象的物理问题进行建模和模拟[38]。基于深度神经网络DNN(Deep Neural Networks)模型，实现了对非均质材料的等效性能的快速预测[42]。基于K-means聚类算法[43]的非监督机器学习方法，成功降低了设计变量的维度，加快了拓扑优化的进程[44]。目前已有相当数量的关于机器学习拓扑优化方法的研究工作，用于提高拓扑优化的计算效率及进行实时的拓扑优化设计。

围绕目前已有的拓扑优化方法，本综述将回顾人工智能方法在拓扑优化领域的发展历程及研究现状。考虑到深度学习为近些年最主流的人工智能研究方向，与其相关的技术和应用研究工作众多，故本综述主要介绍深度学习与拓扑优化相结合的相关工作，而对传统的机器学习算法和人工神经网络算法与拓扑优化相结合的工作仅做简要介绍。本综述不涉及该领域的全部文献，其综述范围有限，且与作者本人的研究兴趣密切相关。

2 机器学习在拓扑优化领域的应用

机器学习ML(Machine Learning)是人工智能的主要子域，也是目前人工智能相关研究中最具实用性、应用最为广泛的方法。区别于人工智能使计算机实现类似人类对知识利用的范性目的，机器学习主要研究基于数据实现自改善的算法，该算法能够从数据中自主分析、学习数据特征，并基于所学习的数据特征进行相关的回归及分类行为，其与人工智能、深度学习的关系如图1所示。为了便于整理，本节仅讨论除人工神经网络外的其他传统机器学习方法，包括K-临近算法KNN(K-Nearest Neighbors)、支持向量回归SVR(Supported Vector Regression)、线性判别器和朴素贝叶斯等学习模型[45]。近些年，将机器学习算法与拓扑优化框架相结合实现快速的拓扑优化设计受到了众多学者的高度关注。

图1 人工智能、机器学习、人工神经网络和深度学习之间的关系

Lei等[46]在MMC拓扑优化框架的基础上，使用KNN与SVR模型实现了拓扑预测。MMC拓扑优化框架具有参数量少的特点，但同样需要多次迭代来满足收敛条件。文中基于建立的机器学习模型给出初步的拓扑构型预测，并将此预测结果代入到MMC优化程序中进行进一步的优化，从而获得最终的拓扑优化构型，这在一定程度上大幅缩减了计算量，且预测结果也能满足精度要求。Jiang等[47]提出了基于机器学习的参数调整策略，将基于极端随机树ET(Extra-Trees)的图像分类器集成到优化框架中，并与粒子群算法(PSO)相结合形成闭环，以实现MMA(Method of Moving Asymptotes)[48]优化超参数的自动调整。结果表明，所提模型能够有效地在给定设计领域内得到合理的参数方案。

含微观特征的结构由于具有更大的设计空间，往往具有更好的产品性能。近些年随着增材制造技术的出现，相应多尺度结构的制造逐渐摆脱了传统制造工艺的束缚，具有极大的发展潜力。然而包含微观结构的拓扑优化相比于宏观拓扑优化具有更高的计算成本。针对上述问题，Kumar等[49]基于K-means聚类方法研究了微观结构拓扑优化问题，降低了微观结构拓扑优化算法的计算成本。Yan等[50]基于K-means聚类方法研究了多尺度热弹性点阵结构的拓扑优化问题。Qiu等[51]基于K-means聚类方法提出了一种并发的拓扑优化方法，用于点阵结构的拓扑优化设计。Zhang等[52,53]基于克里金法(Kriging Method)[54]预测了材料的微观结构属性以加速多尺度的拓扑优化进程。Raponi 等[55]通过将克里金法与水平集方法(Level-set Method)相结合，实现了耐冲击结构拓扑优化设计。

3 人工神经网络与结构拓扑优化

人工神经网络为目前机器学习中最受关注的重要领域。由于良好的可扩充性与强大的非线性处理能力，人工神经网络近乎可以实现任何复杂问题的处理。常规人工神经网络结构如图2所示。其网络结构由输入层、隐含层与输出层组成。其中，输入层负责接收外界输入数据，隐含层负责对传入数据进行维度变换与加工，最终结果由输出层输出。对于人工神经网络的训练，即为基于训练数据对各层神经元间的连接权重与各个神经元的参数进行调整。而随着人工神经网络的发展与不断变革，其网络架构正不断趋于深层化与复杂化。为了便于整理，本节仅对基于结构简单的人工神经网络模型展开的拓扑优化研究工作进行介绍。

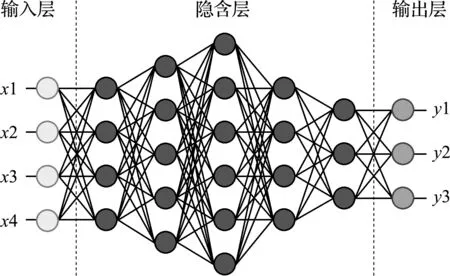
图2 神经网络结构[56]

Ulu等[57]采用主成分分析PCA(Principal Component Analysis)方法与神经网络相结合，进行了二维结构的拓扑优化。使用SIMP拓扑优化方法获得大量的优化结果，并基于PCA方法对优化后的结果图像进行特征降维。PCA方法的权重值与对应载荷情况作为初始数据输入到神经网络模型中进行模型训练。当在训练完成的模型中输入新的载荷信息时，模型也将产生新的PCA权重值，从而组建相对应的优化结果图。这种方法成功实现了快速拓扑预测的功能，降低了优化的计算量。Deng等[58]使用神经网络，探讨了隐含层数量对模型几何特征描述能力的影响，实现了三维结构的快速拓扑预测功能。Ranjbar[59]则是基于全连接神经网络构建了一个关于声学结构的优化框架，并在文献[60]讨论了所提的模型在不同参数设置时的预测性能。Gu等[61]使用单层神经网络预测了双相复合材料的强度和韧性。除了直接用于结构预测，人工神经网络也可用做拓扑优化中分析程序的代理模型。White等[62]将单层神经网络纳入到了多尺度拓扑优化框架，用于预测具有微观结构的超材料等效材料属性。

除了上述人工神经网络与拓扑优化的结合方式外，也有学者尝试将人工神经网络中的寻优算法与拓扑优化框架结合以提高计算效率。Hoyer等[63]利用神经网络对函数的隐偏置来改进拓扑优化的参数，通过优化神经网络的参数，而不是直接优化网格上的密度来实现拓扑优化的过程，结果表明这种方法可以通过网络训练实现更好的设计。Chandrasekhar等[64]将SIMP拓扑优化方法与神经网络相互融合，将神经网络模型作为优化框架的一部分，使用Adam优化器代替了传统SIMP法中的优化求解器。相比于传统的SIMP拓扑优化方法，神经网络与有限元分析相结合的框架可在总体上节约一半的计算成本，大幅提高了运行的效率。

4 深度学习与结构拓扑优化

深度学习DL(Deep Learning)是人工神经网络的重要分支，一般指从输入到输出具有多层结构的神经网络。相比于结构简单的人工神经网络模型，深度学习模型具有更加复杂的层级结构与更加多样化的数据处理方式，具有强大的非线性处理能力。目前常见的深度学习模型主要包括CNN模型、循环神经网络RNN(Recurrent Neural Networks)、自编码器(Autoencoders)、深度置信网络(Deep Belief Nets)和生成对抗网络GAN(Generative Adversarial Networks)等[45]。这些模型在处理复杂关系模拟、大量数据拟合等问题时有着出色的表现。本节根据不同的数据学习模式，详细介绍了以回归拓扑为目的的回归式结构拓扑优化和以生成拓扑为目的的生成式结构拓扑优化的框架和应用，系统归纳了基于相关算法的拓扑优化设计工作。

4.1 回归式结构拓扑优化设计

部分深度学习在拓扑优化方向的应用采用回归拓扑构型的技术路线，即在深度学习模型中仅将拓扑优化问题作为图形的回归问题处理，在模型的构造与使用过程中不考虑目标函数和设计变量取值等拓扑优化要素。其中，CNN模型由于其基于卷积操作实现了对以图像为首的多维数据结构的小参数处理，大幅降低了神经网络结构对多维数据结构的处理难度，是最受工程领域关注的深度学习模型之一，其具体的网络结构如图3所示。CNN模型架构一般包括用于提取数据特征的卷积层和用于数据降维的池化层。二者相结合可以在使用较少参数的同时有效提取图像在各个尺度上的信息。由于CNN模型出色的图形处理能力，学者们将其应用到拓扑优化领域以加速优化进程。Sosnovik等[65]将深度学习模型引入到SIMP拓扑优化之中，提出了一种轻量级的CNN模型模仿拓扑预测过程，以初步迭代的结构密度分布与梯度值作为初始信息，快速获得可靠的拓扑构型，显著加速了拓扑优化的进程。Wang等[66]则是提出了一个具有较强泛化能力的深层CNN模型，通过扩大样本集规模并丰富输入数据类型，来缓和深层深度学习模型的过拟合情况，并增强其泛化能力。Sasaki等[67]构建了一个CNN模型，用于电机结构的最大化平均扭矩设计，基于所训练模型获得的拓扑优化结果与基于传统的拓扑优化所获得的结果相比，在形状和性能上相差不大，但计算成本降低了约10%～33%。不同于上述基于二维拓扑优化问题的研究，Banga等[68]将三维工况下SIMP拓扑优化方法与CNN模型相结合。详细讨论了模型不同通道数据对预测结果精度的影响。经过良好训练深度学习模型，在保证模型预测准确性的基础上，相比于传统的拓扑优化方法，缩短了40%的整体运算时间，显著提升了运行的效率。

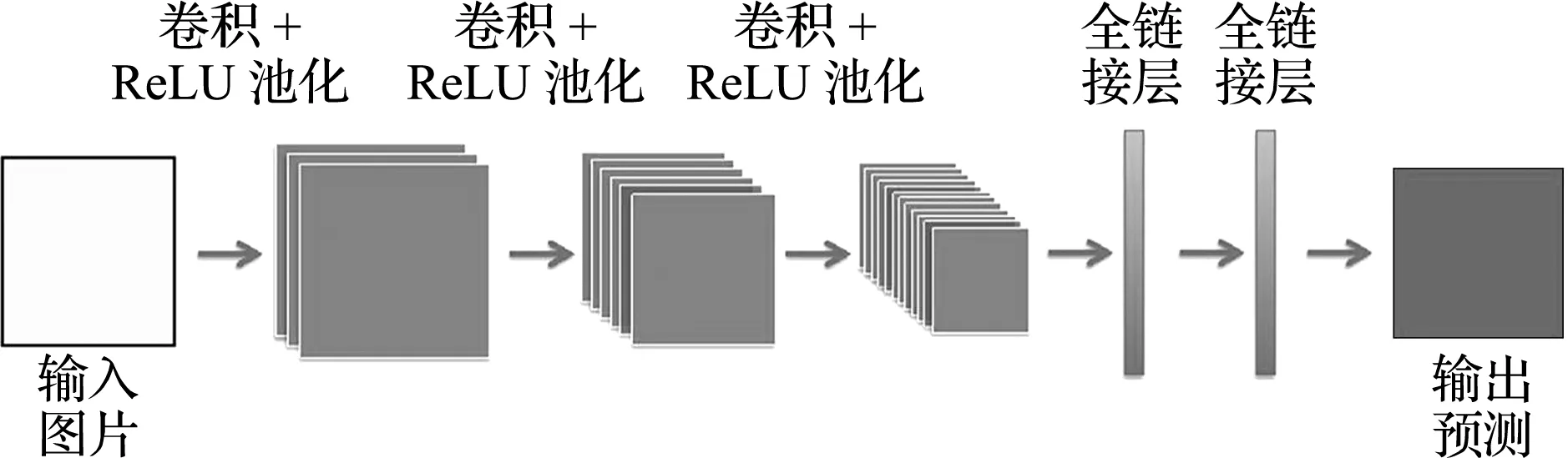
图3 卷积神经网络(CNN)框架[45]

为使传统CNN模型更能适应拓扑优化问题，一些学者对CNN模型进行了改进。Abueidda等[69]将深度特征拼接技术与CNN模型结合，对线弹性小变形问题、具有几何和物理非线性的超弹性响应问题以及线弹性应力约束问题进行了相关的拓扑优化研究，同时使用超级计算机来进行样本集的采集与模型的训练，大幅减少了整体运算时间。为解决传统拓扑优化方法在加大网格数量时，面临的维度诅咒的挑战，Xue等[70]将超分辨率卷积神经网络SRCNN(Super Resolution Convolutional Neural Network)技术引入到拓扑优化框架，并建立了新的池化策略，使得优化过程中的有限元分析数量与输出网格的数量保持平衡，该研究最大的亮点是在处理三维拓扑优化问题时，通过集成多个二维拓扑优化网络进行最优拓扑的预测。此方法既保证了最优拓扑构型的预测质量，也减少了训练三维神经网络的时间成本。Nakamura等[71]在深度学习模型的编码器和解码器中分别使用了批正则化(Batch Normalization)和空间适应去正则化(Spatially Adaptive Denormalization)技术，并表明了在相同模型框架结构下，其模型具有更好的预测精度，实现了在给定任意设计域和边界条件下，无需任何的迭代过程即可实现结构的拓扑优化设计。此外，基于CNN模型还可进行超材料拓扑优化设计[72]和散热结构的拓扑优化设计[73]等。

除CNN模型外，一些学者还基于其他深度学习模型，在拓扑优化领域进行了探索。Deng等[74]指出解决非线性高维的拓扑优化问题需要使用智能优化算法，但是由于其计算量较大，导致相关的拓扑优化面临巨大的挑战。为解决这个问题，提出了一个自主在线学习的深度神经网络，并使之与广义模拟退火模型GSA(Generalized Simulated Annealing)相结合来取代拓扑优化计算中的有限元分析部分，该模型的主要特点是可以动态产生深度学习模型所需要的训练数据，从而避免产生与最优值距离较远的不相关的训练数据，有助于深度学习模型在关键区域实现更好的回归效果，以便做到更准确地预测。该模型可以降低两个数量级以上的计算耗时，为进行大规模三维非线性拓扑优化带来了可能。Bi等[75]提出了一个集成深度学习和并行计算的通用可扩展框架，以提高拓扑优化设计效率。该框架的核心思想是深入挖掘迭代历史数据，利用深度神经网络生成当前拓扑优化设计的代理梯度，在处理一个新的设计问题时，只需要进行在线的自主学习，而不需要前期进行大量的数据采集工作。以大规模基于增材制造的结构设计为例，当前的拓扑优化框架能够显著节约计算成本，与传统的拓扑优化设计相比，可提高设计速度约8.6倍。Yang等[76]提出了一种基于图卷积神经网络GCN(Graph Convolutional Networks)的拓扑优化框架，解决了传统基于CNN拓扑优化框架存在高稀疏性和噪声问题。针对基于梯度的拓扑优化框架，Qian等[77]构建了一个对偶型的神经网络模型(Dual-model Neural Networks)，此模型能够提供较为精确的灵敏度和目标函数的评估，并通过将此模型嵌入到基于梯度的拓扑优化框架内，取代原框架内高维的仿真分析，显著加速了拓扑优化的进程。此外还提出了一个高效的图形训练数据生成方法，降低了训练模型所需的时间成本。基于所构建的模型，分别研究了结构最小柔顺性拓扑优化问题和具有负泊松比的超材料设计问题，两种问题均达到了较为理想的结果。

4.2 生成式结构拓扑优化设计

与回归式设计不同，生成式设计在模型的训练过程中可以考虑模型目标函数、制造可行性及美观性等多种拓扑优化要素与评价方法，上述特点使近年来学者们发展的许多生成式模型，如变分自动编码器VAE(Variational Auto-Encoder)模型和GAN模型等适用于生成式拓扑优化问题研究。以下将分别对两者与拓扑优化的结合应用进行介绍。

GAN模型[78]是深度学习模型的一种，主要由生成器和判别器两个神经网络模型构成，通过两个模型之间的相互博弈，使得生成器模型能够产生与原始样本相近的新样本，达到以假乱真的目的。相比于传统的非监督式学习效率，GAN模型有效提升了相关问题的学习效率，激发了学术界和工业界对深度学习的兴趣与期待，其具体框架如图4所示。

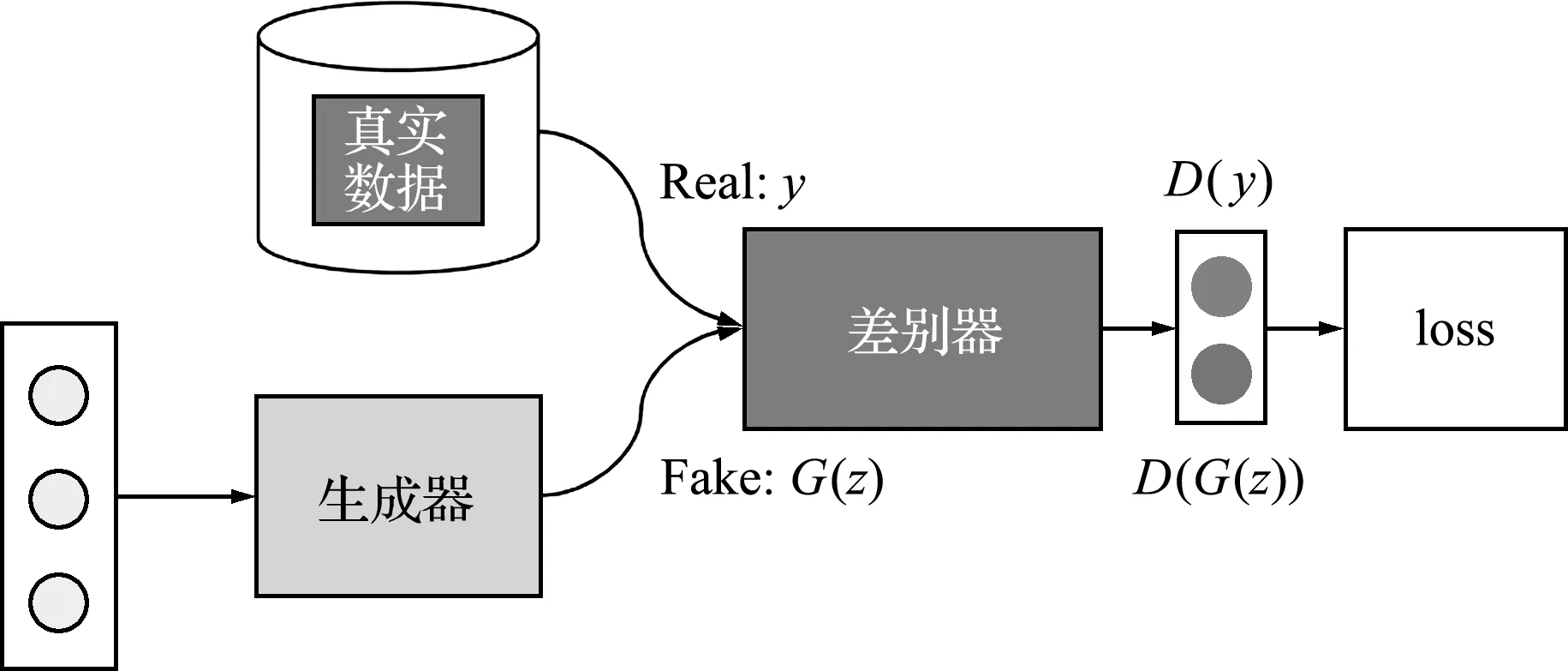
图4 生成对抗网络(GAN)模型框架[79]

一些学者通过引入GAN模型来实现拓扑优化过程。Rawat等[80]在SIMP拓扑优化框架下，基于Wasserstein生成对抗网络(WGAN)实现了特定载荷和特定边界条件下不同材料体积约束与拓扑优化超参数(密度惩罚系数，滤波器半径)设计的生成，同时设计了一套CNN网络，基于WGAN生成的设计，输出材料体积约束与拓扑优化超参数。随后，对WGAN网络进行了修改，将二维拓扑优化设计生成拓展到了三维问题，指出虽然图形预测质量有所下降，但传力路径依旧存在较高的可辨识性[81]。然而，上述工作仅面向单一确定工况的结构拓扑优化问题，实用性有限。Sharpe等[82]基于cGAN[83]框架实现了对任意体积约束、载荷位置的结构的最优拓扑构型预测，利用标准SIMP方法和多尺度方法获得的拓扑优化数据训练了不同的cGAN。上述模型将体分比、负载位置和材料类型设定为网络的输入，以用于快速生成工程师能够使用的初始设计。相比于传统GAN模型，cGAN在生成器输入与判别器输入处均添加了图片的标签向量，并根据该向量重构了模型的训练损失以确保生成器与判别器在对应标签范围内发挥作用。Nie等[84]将挤压激励残差联合网络(U -SE-ResNet)与cGAN相结合，进一步提升了生成器对于拓扑优化问题的生成性能，并实现了根据载荷、边界条件及材料体积约束生成拓扑构型的TopologyGAN框架。对比基本的cGAN框架，针对未知边界条件的问题，所提框架能够使均方误差降低3倍，绝对误差降低2.5倍，大幅提高了最优拓扑结构的预测精度。并且通过上述高维的数据表征方法，该框架的适用性近乎扩展到了全部的拓扑优化问题。通过将图像标签替换为拓扑优化的载荷边界条件，完成了cGAN与拓扑优化的对接。除了约束和载荷较为明确的常规结构拓扑优化问题外，GAN也可用于更为复杂的工程产品拓扑优化中。Oh等[85]基于样本分类、边界平衡生成对抗网络、创新性筛查与优质样本扩充等一系列手段建立了可控制性能与几何约束的GAN设计生成框架，并将该框架用于生成二维轮胎承力结构设计，这些设计选项不仅符合美学，而且具有优良的工程性能。除了二维产品，GAN也可用于更为复杂的三维工程产品生成。Shu等[86]基于点云模型与GAN网络实现了飞行器整机的设计生成。

变分自编码器(VAE)[87]是自编码器的改进版本，通过在传统的自编码器潜在空间Z增加一个正态分布约束，实现对先验数据分布进行建模。其包含编码器和解码器两个部分。编码器将数据分布的高级特征映射到数据的低级表征，低级表征又叫做本征向量。解码器通过吸收数据的低级表征，输出同样数据的高级表征。其具体的框架如图5所示。

图5 自编码器框架

对于没有确定方程描述的问题，基于传统的拓扑优化方法进行优化设计时可能会面临巨大的挑战。Guo等[88]基于SIMP方法生成的样本，构建了一个VAE的生成模型，为上述问题的求解提供了新的求解思路。该方法将二维的拓扑构型代入到一个低维的隐空间中进行相应的优化过程，并通过解码生成一个二维的拓扑构型。基于此方法进行了热传导问题的优化，与传统的拓扑优化框架相比，所建立的模型能够同时提高计算效率及求解质量。为解决传统拓扑优化方法在解决复杂约束问题时面临的挑战，Zhang等[89]基于变分自编码器(VAE)提出了新的结构布局优化设计方法。此方法利用该模型的学习能力学习约束条件，从而自动生成满足所有约束条件的设计对象。上述研究证明了VAE网络能够不基于物理模拟来学习相关设计问题的基本方程，即可生成一种有效的设计。优化结果表明即使基于较为简单的神经网络框架，也能够相对容易地解决不同物理问题，而且不需要进行灵敏度分析。除单目标拓扑优化外，多目标优化中也存在相关的深度学习应用。Yamasaki等[90]将材料体积约束与结构性能同时作为设计变量，对应固定载荷构筑了拓扑优化问题的帕列托前沿解集，并基于该帕列托前沿上的样本点训练了自变分编码器(VAE)拓扑优化框架。完成训练后，仅需更改输入隐变量的数值即可使该模型产生不同的生成图形结果。另外，他们在过去的工作中提出了一种设计域映射方法，以将不规则设计域与载荷映射到规则设计域上进行优化，再将优化结果反映射回不规则设计域。通过将上述方法与VAE拓扑优化框架相结合，使得此方法的普适性在一定程度上获得了扩充。

除了上述基于单一生成模型架构的拓扑优化研究工作之外，一些学者将生成模型与其他神经网络模型结合，形成了基于复杂集成架构的深度学习拓扑优化框架。Tan等[91]提出了一种基于深度卷积生成对抗网络DCGAN(Deep Convolutional Generative Adversarial Networks)和CNN的微结构材料设计深度学习模型，其中DCGAN模型用于生成最优的设计构型，CNN模型用于预测最优构型的相关力学响应。该模型具有处理几何约束简单和效率高的优点。然而，其处理的问题尺度依旧有限。Yu等[79]基于SIMP拓扑优化方法生成的10万个具有不同体分比和边界条件下的拓扑结构，分别训练了基于卷积操作的自编码器(AE)和条件生成对抗网络(cGAN)。其中，AE模型用于根据载荷与边界条件生成最优拓扑构型，其输出用作cGAN模型的输入，以实现图像从低分辨率到高分辨率的增强。所提模型可实现任意给定的边界条件和体分比的近似最优结构拓扑构型预测，并实现分辨率增强以达到多尺度拓扑优化的效果。然而，其展示的结果中，高分辨率拓扑并未展现出密集网格应有的几何细节。

5 结 论

随着工业界对创新构型设计、结构的轻质及高性能等特定功能的需求不断提高，结构拓扑优化方法也在不断根据工程实际使用需求做出相应的创新。为改善传统拓扑优化方法中由于反复迭代及大规模有限元计算导致的计算效率较低的问题，将以机器学习为代表的人工智能方法引入到拓扑优化框架，加速了拓扑优化进程，为实现实时的大规模拓扑优化设计提供了可能。

由文中提及的各项工作的表现效果可以看到，基于机器学习、人工神经网络及深度学习的拓扑优化相关工作很大程度上继承了对应模型的特点，即机器学习模型结构简单，需求的驱动数据较少，易于实现与训练，但模型对于多变量问题的处理能力略有不足；深度学习模型结构复杂，需求驱动数据量大，但模型对多变量和高度非线性问题的处理能力较强；而人工神经网络则居于两者之间。值得关注的问题是，尽管目前通过构建不同的神经网络模型可以对计算速度提供几个数量级的提升。但这些神经网络在训练过程中往往占据大量的计算资源，如以大规模有限元分析为基础的数据累积等。虽然部分神经网络已经对原有的离线学习模型进行了改进，但对整体的拓扑优化效率依然有一定影响。想要真正提高效率，就必须将结构力学原理与模型结合，开发有效的数据生成方法，提高模型训练效率。

增材制造等先进制造技术不断革新，为结构拓扑优化的发展提供了肥沃的土壤，也为具有多功能的复杂拓扑结构提供了制造的可能。在如此注重效率的工业领域，加快拓扑优化进程是提高工业制造效率的首要环节。机器学习和深度学习等智能优化算法与拓扑优化的结合为高效高质的拓扑优化设计提供了新的思路，目前人工智能与拓扑优化相结合尚处于起步阶段，但近年已经呈现出蓬勃发展的势头，期待此领域的学者能够发展出更好的智能算法，将人工智能与拓扑优化进一步联系在一起，建立具有大规模、多功能和鲁棒性强的拓扑优化框架。

参考文献(References):

[1] Guo X,Cheng G D.Recent development in structural design and optimization[J].ActaMechanicaSinica,2010,26(6):807-823.

[2] Michell A G M.LVIII.The limits of economy of material in frame -structures[J].TheLondon,Edinburgh,andDublinPhilosophicalMagazineandJournalofScience,1904,8(47):589-597.

[3] Cheng K T,Olhoff N.An investigation concerning optimal design of solid elastic plates[J].InternationalJournalofSolidsandStructures,1981,17(3):305-323.

[4] Bendsøe M P,Kikuchi N.Generating optimal topolo -gies in structural design using a homogenization method[J].ComputerMethodsinAppliedMechanicsandEngineering,1988,71(2):197-224.

[5] Bendsøe M P.Optimal shape design as a material distribution problem[J].StructuralOptimization,1989,1(4):193-202.

[6] Rozvany G I N,Zhou M,Birker T.Generalized shape optimization without homogenization[J].StructuralOptimization,1992,4(3-4):250-252.

[7] Zhou M,Rozvany G I N.The COC algorithm,Part II:Topological,geometrical and generalized shape optimization[J].ComputerMethodsinAppliedMecha-nicsandEngineering,1991,89(1-3):309-336.

[8] Xie Y M,Steven G P.A simple evolutionary proce -dure for structural optimization[J].Computers&Structures,1993,49(5):885-896.

[9] Allaire G,Jouve F,Toader A M.A level set method for shape optimization[J].ComptesRendusMathematique,2002,334(12):1125-1130.

[10] Wang M Y,Wang X M,Guo D M.A level set method for structural topology optimization[J].ComputerMethodsinAppliedMechanicsandEngineering,2003,192(1-2):227-246.

[11] Guo X,Zhang W S,Zhong W L.Doing topology optimization explicitly and geometrically—A new moving morphable components based framework[J].JournalofAppliedMechanics,2014,81(8):081009.

[12] Zhang W S,Yuan J,Zhang J,et al.A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model[J].StructuralandMultidisciplinaryOptimization,2016,53(6):1243-1260.

[13] Zhang W S,Chen J S,Zhu X F,et al.Explicit three dimensional topology optimization via Moving Morphable Void(MMV)approach[J].ComputerMethodsinAppliedMechanicsandEngineering,2017,322:590-614.

[14] Sui Y K,Yang D Q.A new method for structural topological optimization based on the concept of independent continuous variables and smooth model[J].ActaMechanicaSinica,1998,14(2):179-185.

[15] Burger M,Stainko R.Phase -field relaxation of topo -logy optimization with local stress constraints[J].SIAMJournalonControlandOptimization,2006,45(4):1447-1466.

[16] Takezawa A,Nishiwaki S,Kitamura M.Shape and topology optimization based on the phase field method and sensitivity analysis[J].JournalofComputa-tionalPhysics,2010,229(7):2697-2718.

[17] Bourdin B,Chambolle A.Design-dependent loads in topology optimization[J].ESAIM:Control,Optimi-sationandCalculusofVariations,2003,9:19-48.

[19] Norato J A,Bendsøe M P,Haber R B,et al.A topo -logical derivative method for topology optimization[J].StructuralandMultidisciplinaryOptimization,2007,33(4-5):375-386.

[20] Zhu J H,Zhang W H,Xia L,et al.Optimal packing configuration design with finite-circle method[J].JournalofIntelligent&RoboticSystems,2012,67(3-4):185-199.

[21] Hajela P,Lee E.Genetic algorithms in truss topological optimization[J].InternationalJournalofSolidsandStructures,1995,32(22):3341-3357.

[22] Shim P Y,Manoochehri S.Generating optimal confi-gurations in structural design using simulated annealing[J].InternationalJournalforNumericalMe-thodsinEngineering,1997,40(6):1053-1069.

[23] Luh G C,Lin C Y,Lin Y S.A binary particle swarm optimization for continuum structural topology optimization[J].AppliedSoftComputing,2011,11(2):2833-2844.

[24] Luh G C,Lin C Y.Structural topology optimization using ant colony optimization algorithm[J].AppliedSoftComputing,2009,9(4):1343-1353.

[25] Liu L,Yan J,Cheng G D.Optimum structure with homogeneous optimum truss-like material[J].Computers&Structures,2008,86(13-14):1417-1425.

[26] Yan J,Cheng G D,Liu L.A uniform optimum mate -rial based model for concurrent optimization of thermoelastic structures and materials[J].InternationalJournalforSimulation&MultidisciplinaryDesignOptimization,2008,2(4):259-266.

[27] Niu B,Yan J,Cheng G D.Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency[J].StructuralandMultidisciplinaryOptimization,2008,39(2):115-132.

[28] Fan Z R,Yan J,Wallin M,et al.Multiscale eigenfre -quency optimization of multimaterial lattice structures based on the asymptotic homogenization method[J].StructuralandMultidisciplinaryOptimization,2020,61(3):983-998.

[29] Kim Y Y,Yoon G H.Multi-resolution multi-scale topology optimization—A new paradigm[J].InternationalJournalofSolidsandStructures,2000,37(39):5529-5559.

[30] Jang I G,Kwak B M.Evolutionary topology optimization using design space adjustment based on fixed grid[J].InternationalJournalforNumericalMe-thodsinEngineering,2006,66(11):1817-1840.

[31] Aage N,Andreassen E,Lazarov B S.Topology optimization using PETSc:An easy-to-use,fully parallel,open source topology optimization framework[J].StructuralandMultidisciplinaryOptimization,2015,51(3):565-572.

[32] Aage N,Andreassen E,Lazarov B S,et al.Giga-voxel computational morphogenesis for structural design[J].Nature,2017,550(7674):84-86.

[33] Hinton G E,Salakhutdinov R R.Reducing the dimensionality of data with neural networks[J].Science,2006,313(5786):504-507.

[34] Rumelhart D E,Hinton G E,Williams R J.Learning representations by back-propagating errors[J].Nature,1986,323(6088):533-536.

[35] Gatys L A,Ecker A S,Bethge M.Image style transfer using convolutional neural networks[A].2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR)[C].2016.

[36] Chiu C C,Sainath T N,Wu Y H,et al.State -of-the -art speech recognition with sequence -to -sequence models[A].2018 IEEE International Conference on Acoustics,Speech and Signal[C].2018.

[37] Gehring J,Auli M,Grangier D,et al.Convolutional sequence to sequence learning[A].34t hInternational Conference on Machine Learning,ICML 2017[C].2017.

[38] Farimani A B,Gomes J,Pande V S.Deep learning the physics of transport phenomena[EB/OL].2017.

[39] LeCun Y,Boser B,Denker J S,et al.Backpropagation applied to handwritten zip code recognition[J].NeuralComputation,1989,1(4):541-551.

[40] Guo X X,Li W,Iorio F.Convolutional neural networks for steady flow approximation[A].Proceedings of the 22n dACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C].2016.

[41] Mirza M,Osindero S.Conditional generative adversarial nets[J].ComputerScience,2014:2672-2680.

[42] Li X,Liu Z L,Cui S Q,et al.Predicting the effective mechanical property of heterogeneous materials by image based modeling and deep learning[J].Compu-terMethodsinAppliedMechanicsandEngineering,2019,347:735-753.

[43] Chang D X,Zhang X D,Zheng C W.A genetic algo -rithm with gene rearrangement for K-means cluste -ring[J].PatternRecognition,2009,42(7):1210-1222.

[44] Liu K,Tovar A,Nutwell E,et al.Towards nonlinear multimaterial topology optimization using unsupervised machine learning and metamodel-based optimization[A].Proceedings of ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference[C].2016.

[46] Lei X,Liu C,Du Z L,et al.Machine learning-driven real-time topology optimization under moving morphable component-based framework[J].JournalofAppliedMechanics,2019,86(1):011004.

[47] Jiang X C,Wang H,Li Y,et al.Machine Learning based parameter tuning strategy for MMC based to -pology optimization[J].AdvancesinEngineeringSoftware,2020,149:102841.

[48] Svanberg K.The method of moving asymptotes —A new method for structural optimization[J].InternationalJournalforNumericalMethodsinEnginee-ring,1987,24(2):359-373.

[49] Kumar T,Suresh K.A density-and-strain-based K-clustering approach to microstructural topology optimization[J].StructuralandMultidisciplinaryOptimization,2020,61(4):1399-1415.

[50] Yan J,Sui Q Q,Fan Z R,et al.Clustering-based multiscale topology optimization of thermo -elastic lattice structures[J].ComputationalMechanics,2020,66(4):979-1002.

[51] Qiu Z,Li Q H,Liu S T,et al.Clustering-based concurrent topology optimization with macrostructure,compo -nents,and materials[J].StructuralandMultidisciplinaryOptimization,2021,63(3):1243-1263.

[52] Zhang Y,Gao L,Xiao M.Maximizing natural frequencies of inhomogeneous cellular structures by Kriging-assisted multiscale topology optimization[J].Computers&Structures,2020,230:106197.

[53] Zhang Y,Xiao M,Zhang X Y,et al.Topological design of sandwich structures with graded cellular cores by multiscale optimization[J].ComputerMethodsinAppliedMechanicsandEngineering,2020,361:112749.

[54] Kleijnen J P C.Kriging metamodeling in simulation: A review[J].EuropeanJournalofOperationalRe-search,2009,192(3):707-716.

[55] Raponi E,Bujny M,Olhofer M,et al.Kriging-assisted topology optimization of crash structures[J].ComputerMethodsinAppliedMechanicsandEnginee-ring,2019,348:730-752.

[56] 周志华.机器学习[M].北京:清华大学出版社,2016.(ZHOU Zhi-hua.MachineLearning[M].Beijing:Tsinghua University Press,2016.(in Chinese))

[57] Ulu E,Zhang R S,Kara L B.A data-driven investigation and estimation of optimal topologies under variable loading configurations[J].ComputerMethodsinBiomechanicsandBiomedicalEngineering:Imaging&Visualization,2016,4(2):61-72.

[58] Deng H,To A C.Topology optimization based on deep representation learning (DRL) for compliance and stress -constrained design[J].ComputationalMechanics,2020,66(2):449-469.

[59] Ranjbar M.Fast vibroacoustic optimization of me -chanical structures using artificial neural networks[J].InternationalJournalofMechanicalEnginee-ringandApplications,2013,1(3):64.

[60] Ranjbar M,Saffar M G.A sensitivity analysis on application of artificial neural networks in structural acoustics[EB/OL].2016.

[61] Gu G X,Chen C T,Buehler M J.De novo composite design based on machine learning algorithm[J].ExtremeMechanicsLetters,2018,18:19-28.

[62] White D A,Arrighi W J,Kudo J,et al.Multiscale topology optimization using neural network surrogate models[J].ComputerMethodsinAppliedMechanicsandEngineering,2019,346:1118-1135.

[63] Hoyer S,Sohl-Dickstein J,Greydanus S.Neural reparameterization improves structural optimization[J].2019.

[64] Chandrasekhar A,Suresh K.TOuNN:Topology optimization using neural networks[J].StructuralandMultidisciplinaryOptimization,2021,63(3):1135-1149.

[65] Sosnovik I,Oseledets I.Neural networks for topology optimization[J].RussianJournalofNumericalAna-lysisandMathematicalModelling,2019,34(4):215-223.

[66] Wang D L,Xiang C,Pan Y,et al.A deep convolu-tional neural network for topology optimization with perceptible generalization ability[J].EngineeringOptimization,2021:1-16.

[67] Sasaki H,Igarashi H.Topology optimization accele -rated by deep learning[J].IEEETransactionsonMagnetics,2019,55(6):1-5.

[68] Banga S,Gehani H,Bhilare S,et al.3D topology optimization using convolutional neural networks[EB/OL].2018.

[69] Abueidda D W,Koric S,Sobh N A.Topology optimization of 2D structures with nonlinearities using deep learning[J].Computers&Structures,2020,237:106283.

[70] Xue L,Liu J,Wen G L,et al.Efficient,high-resolution topology optimization method based on convolutional neural networks[J].FrontiersofMechanicalEngineering,2021,16(1):80-96.

[71] Nakamura K,Suzuki Y.Deep learning-based topological optimization for representing a user-specified design area[EB/OL].2020.

[72] Kollmann H T,Abueidda D W,Koric S,et al.Deep learning for topology optimization of 2D metamaterials[J].Materials&Design,2020,196:109098.

[73] Lin Q Y,Hong J,Liu Z,et al.Investigation into the topology optimization for conductive heat transfer based on deep learning approach[J].InternationalCommunicationsinHeatandMassTransfer,2018,97:103-109.

[74] Deng C,Wang Y,Qin C,et al.Self-directed online machine learning for topology optimization[J].2020.

[75] Bi S,Zhang J,Zhang G.Scalable deep -learning-accelerated topology optimization for additively manufactured materials[J].2020:1-9.

[76] Yang L,Kang Z S,Cao X C,et al.Topology optimization based graph convolutional network[A].Procee -dings of the 28t hInternational Joint Conference on Artificial Intelligence[C].2019.

[77] Qian C,Ye W J.Accelerating gradient-based topology optimization design with dual-model artificial neural networks[J].StructuralandMultidisciplinaryOptimization,2021，63(4):1687-1707.

[78] Goodfellow I,Pouget-Abadie J,Mirza M,et al.Gene -rative adversarial networks[J].CommunicationsoftheACM,2020,63(11):139-144.

[79] Yu Y,Hur T,Jung J,et al.Deep learning for determining a near-optimal topological design without any iteration[J].StructuralandMultidisciplinaryOptimization,2019,59(3):787-799.

[80] Rawat S,Shen M H H.A novel topology design approach using an integrated deep learning network architecture[J].2018.

[81] Rawat S,Shen M H.Application of adversarial networks for 3D structural topology optimization[A].SAE Technical Paper Series[C].2019.

[82] Sharpe C,Seepersad C C.Topology design with conditional generative adversarial networks[A].Procee -dings of ASME 2019 International Design Enginee -ring Technical Conferences and Computers and Information in Engineering Conference[C].2019.

[83] Mirza M,Osindero S.Conditional generative adversarial nets[J].2014.

[84] Nie Z G,Lin T,Jiang H L,et al.Topologygan:To -pology optimization using generative adversarial networks based on physical fields over the initial do -main[J].JournalofMechanicalDesign,2021,143(3):031715.

[85] Oh S,Jung Y,Kim S,et al.Deep generative design:Integration of topology optimization and generative models[J].JournalofMechanicalDesign,2019,141(11):1-22.

[86] Shu D L,Cunningham J,Stump G,et al.3D design using generative adversarial networks and physics -based validation[J].JournalofMechanicalDesign,2020,142(7):1-51.

[87] Kingma D P,Welling M.Auto-encoding variational bayes[A].2n dInternational Conference on Learning Representations,ICLR 2014-Conference Track Pro -ceedings[C].2014.

[88] Guo T H,Lohan D J,Cang R J,et al.An indirect design representation for topology optimization using variational autoencoder and style transfer[A].2018 AIAA/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference[C].2018.

[89] Zhang Y J,Ye W J.Deep learning-based inverse method for layout design[J].StructuralandMultidisciplinaryOptimization,2019,60(2):527-536.

[90] Yamasaki S,Yaji K,Fujita K.Data-driven topology design using a deep generative model[J].2020.

[91] Tan R K,Zhang N L,Ye W J.A deep learning-based method for the design of microstructural materials[J].StructuralandMultidisciplinaryOptimization,2020,61(4):1417-1438.