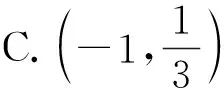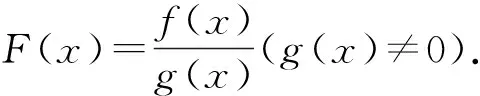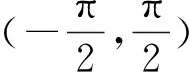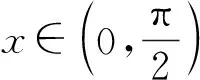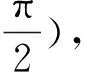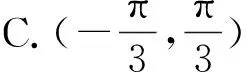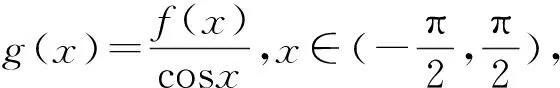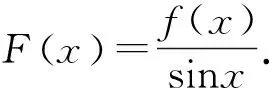具有导函数的抽象函数不等式问题的求解策略*
2021-09-06福建省莆田第二中学351131谢新华
福建省莆田第二中学 (351131) 谢新华
*福建省教育科学“十三五”规划课题2020年度教育教学改革专项课题:学科素养视域下“读思达”教学法的数学课堂应用研究(项目编号:Fjjgzx20-077).
解题中若遇到有关不等式、方程及最值之类的问题,常常需要设法建立起目标函数,确定变量的限制条件,再通过研究函数的单调性、最值等问题,使问题变得明了,所以解这类不等式的通法就是构造合适的函数.本文例举含导函数及其抽象函数不等式问题求解的一般策略.
类型一:f′(x)g(x)±f(x)g′(x)型
例1 已知定义在R上的可导函数f(x),对于任意实数x都有f(-x)=f(x)-2x成立,且当x∈(-∞,0]时,都有f′(x)<2x+1成立.若f(2m)-3m2 例2 设f(x),g(x)分别是定义在R上的奇函数和偶函数,f′(x),g′(x)为其导函数,当x<0时,f′(x)·g(x)+f(x)·g′(x)>0且g(-3)=0,则不等式f(x)·g(x)<0的解集是( ). A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3) C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3) 解析:设F(x)=f(x)g(x),当x<0时,F′(x)=f′(x)·g(x)+f(x)·g′(x)>0,所以F(x)在(-∞,0)上为增函数,因为f(x),g(x)分别是定义在R上的奇函数和偶函数,所以f(-x)=-f(x),g(-x)=g(x),所以F(-x)=f(-x)g(-x)=-f(x)g(x)=-F(x),即F(x)为R上的奇函数.所以F(x)在(0,+∞)上为增函数.又因为g(-3)=0,故有F(-3)=F(3)=0.所以x∈(-∞,-3)∪(0,3)时,f(x)·g(x)<0.故选D. 类型二:xf′(x)±nf(x)型 例3 已知函数f(x)的定义域为(0,+∞),且3f(x)+xf′(x)>0恒成立,其中f′(x)是f(x)的导函数,若(m-2020)3f(m-2020)>f(1),则实数m的取值范围是( ). A.(2019,2020) B.(2019,2021) C.(2019,+∞) D.(2021,+∞) 例4 函数f(x)的定义域为(-∞,0)∪(0,+∞),f′(x)是导函数,且满足xf′(x)-2f(x)>0,若f(x)是偶函数,f(1)=1,则不等式f(x)>x2的解集为________________. 类型三:f′(x)±λf(x)型 例5 已知f′(x)是定义在R上的函数f(x)的导函数,且f(x)+f′(x)>0,则a=2f(ln2),b=ef(1),c=f(0)的大小关系为________________. 解析:设g(x)=f(x)ex,则g′(x)=f′(x)ex+f(x)ex=ex[f′(x)+f(x)],因为f(x)+f′(x)>0对于x∈R恒成立,所以g′(x)=ex[f′(x)+f(x)]>0,所以g(x)=f(x)ex在R上单调递增,a=2f(ln2)=eln2f(ln2)=g(ln2),b=ef(1)=e1f(1)=g(1),c=f(0)=e0f(0)=g(0),因为0 例6 若函数y=f(x)的定义域为R,对于∀x∈R,f′(x) A.(2,+∞) B.(0,+∞) C.(-∞,0) D.(-∞,2) 类型四:sinx·f′(x)±cosx·f(x)或cosxf′(x)±sinx·f(x)型