一道函数不等式试题的多种证法

江西省高安中学 (330800) 朱细秀

试题(雅礼中学2021年模考试题)已知函数f(x)=aex+2x-1(期中e为自然对数的底数).

(1)讨论f(x)的单调性；(2)证明：对任意的a≥1，当x>0时，f(x)≥(x+ae)x.

分析：要证函数不等式，主要是利用函数的导数，通过单调性判断作出证明，但求导前都必须对函数式进行变形，不同的变形就可得到不同的证明路径，函数不等式证明的一般途径为：变形——求导——探讨导数值与0的大小——由单调性确定不等式成立的条件.

解：(1)∵f(x)=aex+2x-1,∴f′(x)=aex+2.

(ⅰ)a≥0时，f′(x)>0,∴f(x)在(-∞，+∞)上单增.

评注：上述证法中，根据题设条件，a≥1,x>0得出ax>0，故在对函数式变形中，两边同除ax，使得后面的求导能找到公因式x-1，剩下只要简证一下ex>x+1，由此g′(x)与0的关系立见分晓.

(法2)欲证aex+2x-1≥x2+aex，即证aex-aex≥x2-2x+1=(x-1)2②.∵a≥1,∴aex-aex=a(ex-ex)≥ex-ex.令g(x)=ex-ex,则g′(x)=ex-e.∴当x∈(0,1)时，g′(x)<0，∴g(x)在(0,1)上单减，x∈(1,+∞)时，g′(x)>0,∴g(x)在(1,+∞)上单增，∴g(x)在x=1时取最小值，且g(x)min=g(1)=0,∴g(x)≥0.∴当x=1时，②成立.

评注：证法2与证法1的变形及思想方法一致，先进行放缩，a(ex-ex)≥ex-ex，然后两边同除以x得到类似表达式，后面的求导等证法基本雷同.类似地，对②式进行以变形还可得另一类似证法.

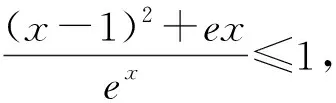
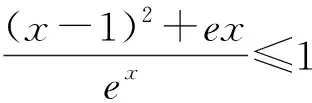
(法3)原不等式等价于aex-x2-eax+2x-1≥0，令g(x)=aex-x2-aex+2x-1，则g′(x)=aex-2x-ae+2=a(ex-e)-2(x-1)，g″(x)=aex-2③.

(ⅰ)当a≥2时，g″(x)>0，∴g′(x)在(0，+∞)上单增，又g′(1)=0，x∈(0,1)g′(x)<0,g(x)在(0,1)单减，x∈(1,+∞),g′(x)>0,g(x)在(1，+∞)单增.∴g(x)≥g(1)=0.

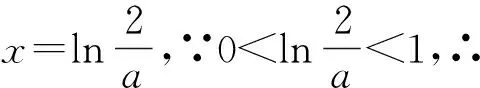
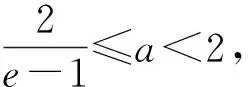
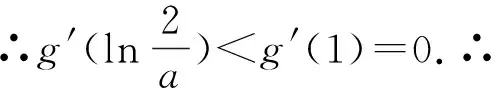
评注：证法3对函数表达式不做任何变形，只进行了移项，然后进行了二次求导，并对a分类讨论，在各种情况下，确定g′(x)的单调性，最后得到g(x)的最小值等于零，证明不等式成立.显然，证法3证明过程最复杂，所以求解中注重适当变形，对证题有事半功倍之效.