条件转化法在数学解题中的运用举隅

江西省吉安市第一中学 (343000) 郭天平 李作滨

条件转化在数学解题中几乎无处不在，我们若能掌握这种转化策略，在遇到一些数量关系复杂、隐蔽而难以解决的问题时，就可使生疏的问题熟悉化、抽象的问题具体化、复杂的问题简单化，从而顺利解决问题[1].常见的条件转化方法有直接转化法、换元法、数形结合法、等价转化法等，本文列举几例予以说明.

例1 已知函数f(x)为二次函数，它的最小值为1，且对任意x∈R，都有f(1+x)=f(1-x)成立，又f(0)=3.求f(x)的解析式.

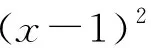
评注：本题就是把原问题直接转化为基本定理、基本公式或者基本图形问题，由问题直接转化，得出结论.

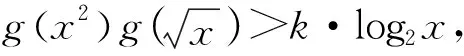
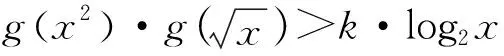
评注：本题是运用换元法，使生疏的问题熟悉化，把无理式转化为有理式或者使整式降幂等，把复杂的问题转换成简单问题，从而解决问题.

例3 若对任意的k∈[-1,1]，函数f(x)=x2+(k-4)x+4-2k的值恒大于零，求x的取值范围.

析解1：本题给的已知条件是k的范围，应用函数换元思想，可以把式子转化为关于k的一元一次不等式g(k)=(x-2)k+x2-4x+4>0，在k∈[-1,1]时恒成立.只需要g(-1)>0且g(1)>0，即x2-5x+6>0且x2-3x+2>0，解得x<1或x>3.

析解2：本题也可以从另外一个角度进行条件转化，结合一元二次函数图形来分析.考虑画出函数f(x)=x2+(k-4)x+4-2k=(x-2)[x-(2-k)]的图像，图像与x轴有两交点分别是2和2-k，结合k∈[-1,1]，2-k∈[1,3]，知函数图像随着k取值变化而变动.作出抛物线图像，易得要使得能够满足函数取值恒大于零的条件为x<1或x>3.

析解3：本题还可转化为一元二次函数与一次函数交点问题来处理.函数f(x)=x2+(k-4)x+4-2k的值恒大于零，即为x2-4x+4>k(2-x)对任意的k∈[-1,1]恒成立，也即函数y=x2-4x+4的图像恒在y=k(2-x)图像上方，所以满足条件的x值为x<1或x>3.

评注：在研究函数问题时，常借助函数的图像特征，对判别式、给定区间端点的函数值、对称轴与该区间的相对关系进行全面综合应用.

图1

析解：本题常规解法可以利用求根公式，也可以结合函数的图形来分析，但要特别注意条件之间转换的等价性，如果转换不等价，就会出错.

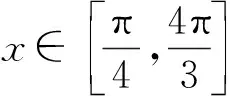
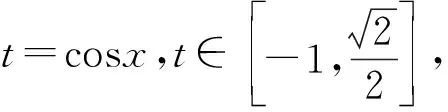
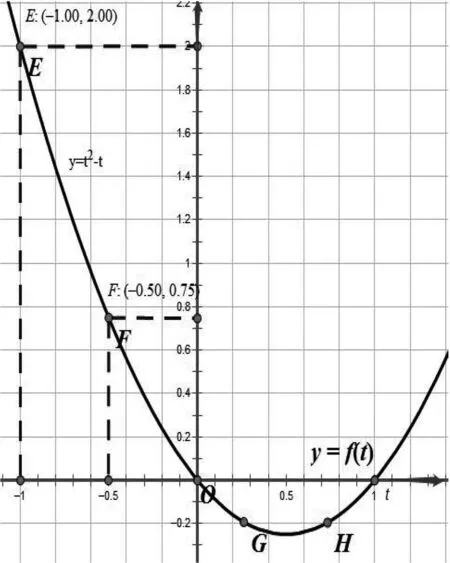
图2

评注：等价转化法就是把原问题的形式向特殊化形式转化，并证明特殊化后的问题和结论都适合原问题.分析发现，在进行条件转化的过程中，要进行等价转化，图像之间的转化也是等价的，对于重合的图像，要单独分析，从而确保解的个数不重不漏.

综上可见，一个数学问题的解决，关键就在于如何合理使用条件转化解决问题，将条件进行转化是解决问题的一般策略.