一个不等式与两道数学竞赛题的拓广

江西省共青城市国科共青城实验学校 (332020) 姜坤崇 黄立才

本文给出一个带两个参数的三元不等式，并应用它简洁证明两道数学竞赛不等式问题的拓广结论.

设三个正数变元是x,y,z,p,q是非负参数，则有如下一个不等式：

命题设x,y,z>0,p≥0,q≥0,且p、q不全为零，s=x+y+z,则

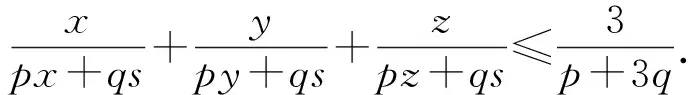
证明：当p=0或q=0时不等式①显然成立，以下设p>0,q>0.①式等价于

由柯西不等式知以上不等式成立，故不等式①得证.

下面用不等式①给出两道数学竞赛不等式试题拓广结论的证明.

题1 (2000年澳门数学竞赛试题)已知a,b,c∈R+,且abc=1,求证：

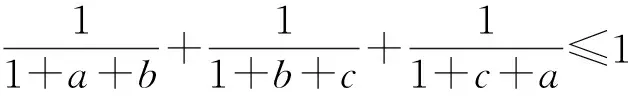
将以上不等式拓广，可得

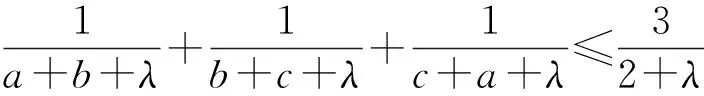
当且仅当a=b=c=1时，③式等号成立.

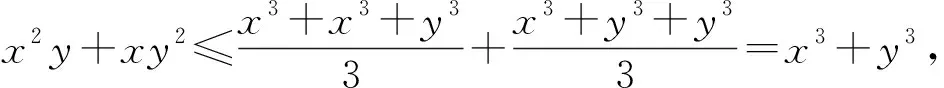
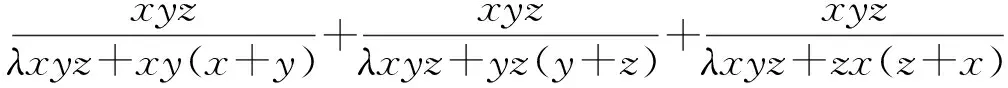
令p=λ-1≥0,q=1,则由不等式①得

从以上证明可以看出，当且仅当x=y=z=1时上式中等号成立，故③式成立，当且仅当a=b=c=1时等号成立.

说明：(1)在不等式③中，令λ=1即得不等式②.

(2)结论1亦即《中等数学》数学奥林匹克问题高343，供题人提供的解答较繁，且不易推广.

(3)根据不等式③及以上证明，不难将结论1推广为：

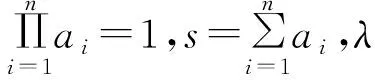
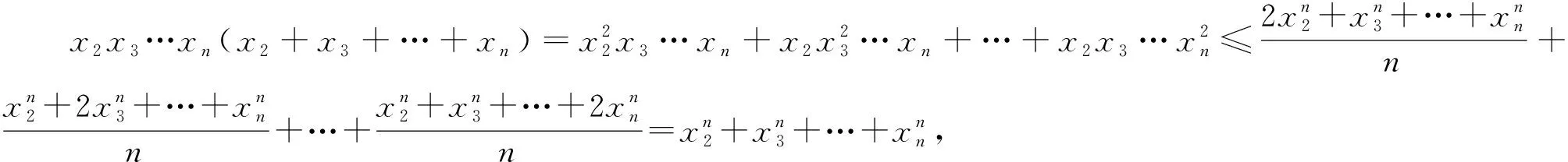
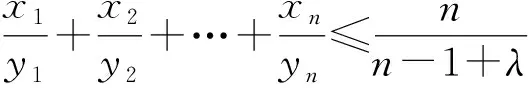
而由柯西不等式知上式成立，即⑤式成立，从而不等式④得证.

将以上不等式拓广，可得：

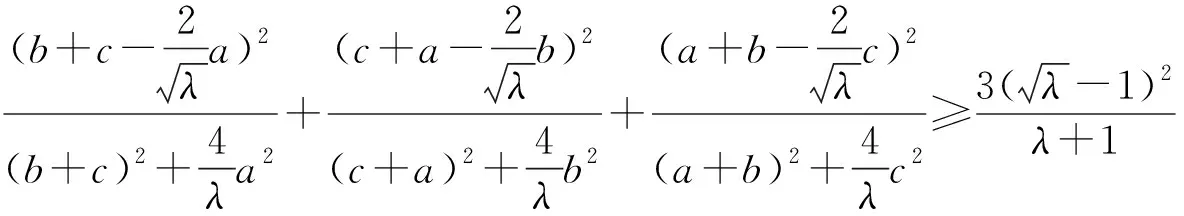
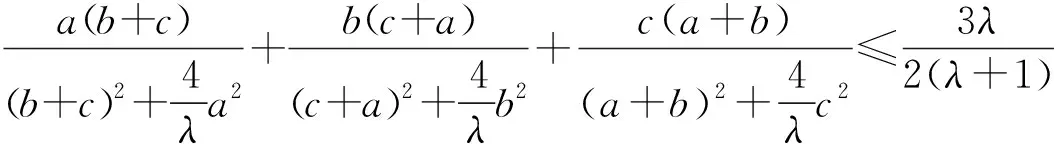
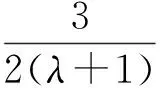
说明：(1)在不等式⑦中，令λ=4即得不等式⑥；

(2)以上结论3不但改进了文献[1]中的结论1，而且这里借助①式给出的证明也较文献[1]给出的结论1的证明简洁得多.