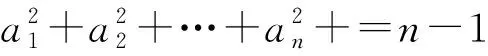若干2021年数学奥林匹克不等式题的巧思妙证
2021-09-06南昌大学附属中学330047温伟明
中学数学研究(江西) 2021年8期
南昌大学附属中学 (330047) 温伟明
笔者对新近出现的一些数学奥林匹克不等式题进行了深入而广泛的研究和探索,拈取数题写就本文,期冀对老师与同学在教学研究中有所启发和帮助.
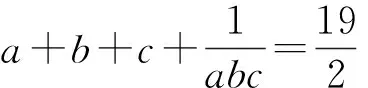
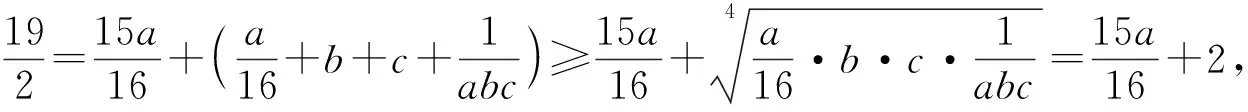
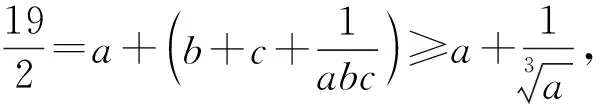
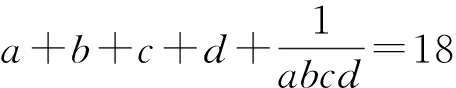
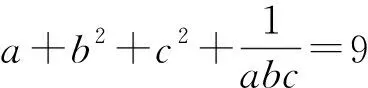
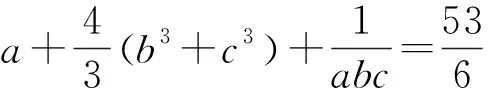

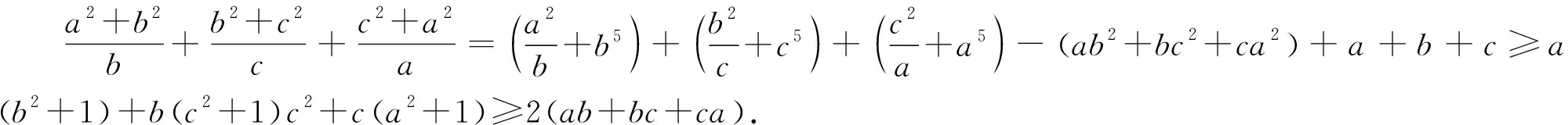
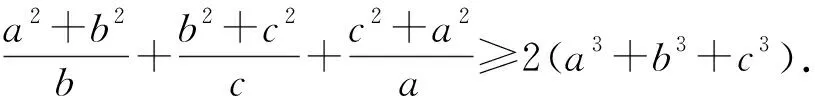
例3 (2021年西班牙数学奥林匹克试题)已知a,b,c,d是满足a+b+c+d=0和a2+b2+c2+d2=12的实数,求abcd的最大值和最小值.
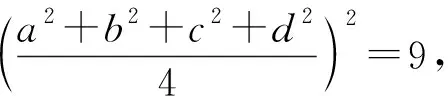
例4 (2021年菲律宾数学奥林匹克试题)已知a,b,c,d是满足a≥b≥c≥d,a+b+c+d=13和a2+b2+c2+d2=43的实数,求证:ab≥3+cd.
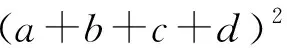
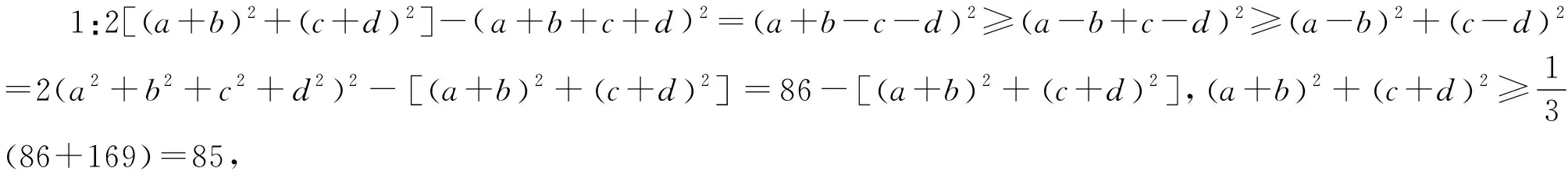
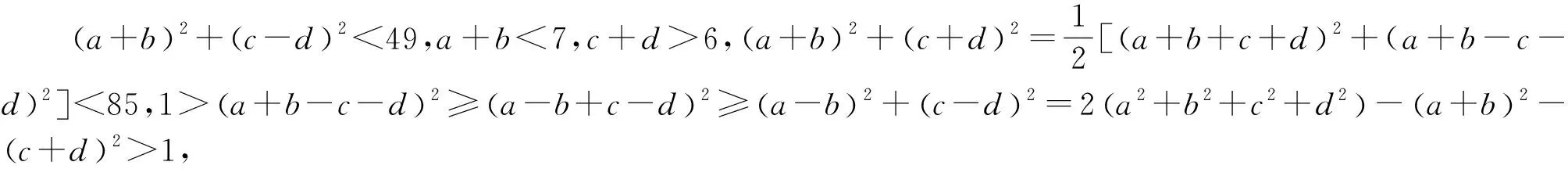
例5 (2021年乌克兰数学奥林匹克试题)已知a,b,c是满足a+b+c=3的非负实数,求证:(3a-bc)(3b-ca)(3c-ab)≤8.
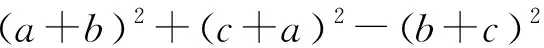
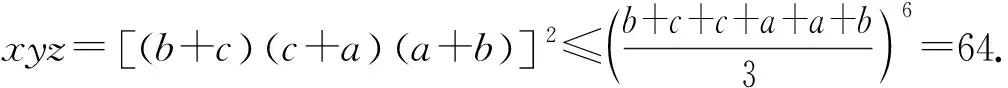
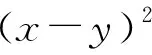
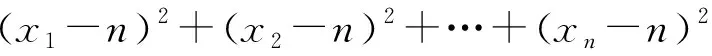

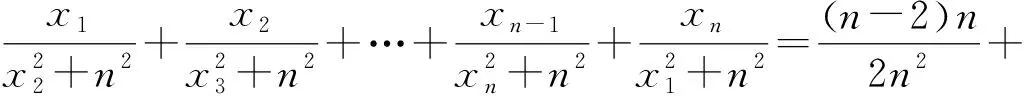
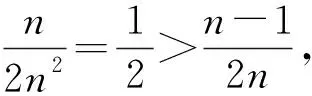
下面证明:当x1,x2,…,xn均为正数时,原不等式成立.
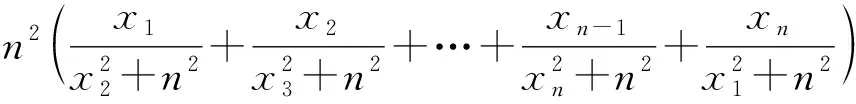
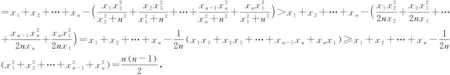
文末,我们给出一道十分漂亮的不等式题(1991波兰数学奥林匹克试题的推广),留给读者探索和研讨: