基于学情分析实现中学高效课堂的对策探究

林希光

摘 要：新课改下，尊重学生主体地位，以多种手段营造高效课堂，为教学工作宗旨所在，而精准的学情分析是高效课堂的有力保障，为因材施教的前提及关键。鉴于此，教师应认真研究课标，以本学科双向目标为核心，进行课堂教学精心设计，拟定针对性教学方案。文章以“角的度量”为例，基于前测，予以学情把握，并基于学情，唤醒经验、感悟本质、巩固技能，以触发学生“生长点”、推进“内化点”、强化“关键点”，经由学生真正需要的教学活动的设计，实现课堂的有效及高效性，推动教学相长。

关键词：精准化;学情分析;小学数学;生本教育;高效课堂

一、 基于前测 把握学情

角的度量是学生在二年级初步认识直角、钝角、锐角的基础上，对角的大小概念进一步理解和拓展，属于小学阶段学生必须掌握的操作技能之一，是教学中公认的难点。

在平时的教学中，教师们通常从角的大小比较开始，希望学生在一步又一步的比较中感悟。要想准确测量出角的大小，必须要有测量标准（测量单位）和测量工具，从而引出量角器和角的单位1度。根据这样的思路，第一次备课时，我们为了让学生感悟度量单位的产生的必要性以及度量的本质，我们在导入部分做了如下教学设计。

导入：尝试比较角的大小

（一）用重叠法比较活动角的大小

师：能比较出这两个角的大小吗？

生：∠1更大。

师：有办法验证一下吗？

生：将两个角的一条边对齐，看另一条边的位置。

师：用重叠法可以比价两个角的大小。

（二）利用三角尺比较练习单上两个角的大小

师：那练习单上这两个角呢？还能用重叠法比较大小吗？

生：不能，因为拿不下来。

师：那该怎么办？试着想办法比一比，有困难的同学可以借助三角尺比一比。

生1：用活动角做出两个与这两个角分别相同的角，进行比大小。

生2：用三角尺帮忙比较。我用三角尺中的这个最小的角放进去，发现∠1比两个最小角多一些，而∠2比两个最小角多较多，所以∠2比较大。

（三）度量单位产生的必要性

师：同学们通过操作，都比较出两个角的大小，那∠2到底比∠1大多少呢？可以怎么办？

生：用更小的角再量一量。

师：那如果还是量不出结果呢？

生：用更更小的角再量一量。

师：要小到什么程度呢？请同学们阅读课本内容。

从以上的教学过程看出，教师在导入环节花费了很多时间引导学生对两个不同大小的角进行比较，期望学生通过比较体验度量标准不断细化的过程，感悟度量单位产生的必要性，从而引出角的度量单位——1度。

然而，在实际教学过程中我们发现，学生对此方案存在诸多的困惑，其中最明显的表现是，当教师让学生对练习单上两个角进行比较时，很多学生就已经喊出“可以用量角器量一量”，但是教师却坚持让学生先用三角尺上的角比一比，这一要求让不少学生感到困惑。此外，在本课后续的教学中发现，用三角尺上的固定角来表示其他角的大小，并没有为后面度量本质的理解起到铺垫作用，部分学生仍然不能很快地明白几度角实际上就是表示这个角里包含了几个1度角。

出现这样的问题，究其原因，是教师没能准确把握学生的学习起点，因此，这样的教学设计是低效甚至是无效的。那么，如何准确把握学生的认知起点？教学前测为我们提供了有力的帮助。

【前测对象】四年级一班共51名学生

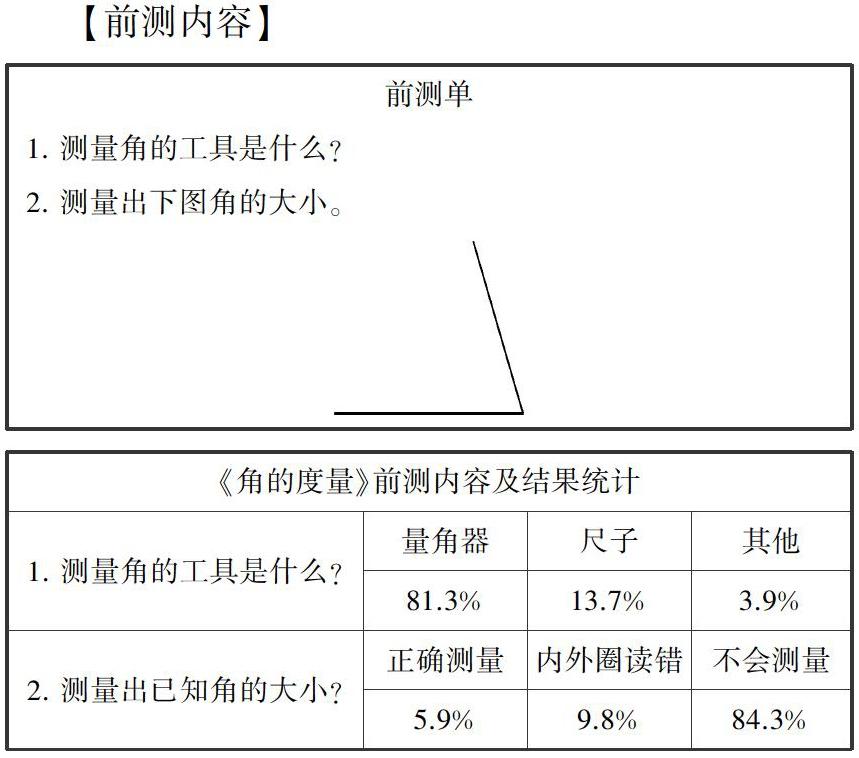
【前测内容】

随后，我们又随机抽取10名学生进行访谈，访谈内容为：

1. 你怎么知道量角器的？2. 你知道角的单位是什么吗？3. 角的单位长什么样？

访谈发现，学生们知道量角器的主要原因是购买的三角尺套装中包含有量角器，从父母或同学的口中知道了这个半圆形的尺子是用来测量角的度数的，至于怎样测量，并没有得到明确答复，而个别学生测量正确的原因多是来自课外辅导班提前学习或是家长的辅导;访谈中还发现，部分学生知道角的单位是“度”，但仅是停留在听说，并不真正了解该单位所表示的意义;继续追问：度量角的单位应该是什么样的？只有一位学生指出角的单位“可能是一个角”，至于为什么这么想，学生无从说起。但是经过提示：“测量线段长度的单位是一条线，测量面积的单位是一个面，那么测量角的单位会是什么样的？”有7位学生能够快速地反应过来，应该是个角。继续追问：应该是个怎样的角？大多数学生认为只能是比较小的角，并且必须要有一个统一的标准，否则每个人测量出来的结果就不一样了。

透过前测、访谈我们不难发现，绝大多数学生知道量角器是测量角度的工具，但是不知道如何准确地使用量角器。在没有任何提示的情况下，学生对于角的单位的理解不够深入，但是当我们把角的单位的认识放置于整个度量体系中，通过唤醒对长度单位、面积单位的认识经验，能够帮助学生感悟角的度量实际上就是看大角里包含有几个小角。学生在之前的学习中，已经经历了统一长度单位、面积单位的必要性，而角的度量单位同样也必然要统一标准才能保证测量结果的一致性。

二、 基于学情 精准设计

面对前测结果，引发笔者思考：1. 如何让学生理解量角器的构造原理;2. 如何在理解度量本质的基础上掌握量角器量角的技巧;

3. 如何幫助学生积累量角的活动经验。基于这样的思考，笔者将教学终点定位为“把握度量本质，积累活动经验”，并围绕这一目标从以下几点展开设计。

（一）唤醒经验，触发“生长点”

教师组织学生参与数学活动、体验知识的形成全过程，引领学生反思回顾学习历程，有助于学生生成或积累相对完整的数学活动经验。如能将学生的认知建立在已有经验的基础上，触发学习生长点，将有助于学生认清知识之间的联系，建构完善的知识体系。